堆本体抗震试验动力相似关系推导与验证

刘 强，王明政，李 楠，李保超

(1.中国原子能科学研究院 反应堆工程技术研究部，北京 102413；2.原兴核技术有限公司，北京 102488)

池式钠冷快堆堆本体环形柱域腔室内具有较大自由液面，受到低频地震激励作用会发生晃动，如何准确计入堆容器及堆内构件液-固边界处的液体晃动载荷，量化液体晃动过程中对堆本体支承裙产生倾覆力矩，是当前池式钠冷快堆堆本体抗震试验研究的重点。

关于地震作用下的液体晃动及相关动力相似准则的研究成果较多，如Abramson[1]、Ewart[2]、Bauer[3]、Lomen[4]、Kornecki[5]在假定容器为刚性结构且流体不可穿透，流体无旋、无黏、不可压，并忽略毛细作用和表面张力的前提下，采用势流理论推导了流体域自由晃动和受迫简谐晃动运动方程的一般形式。Ibrahim[6]推导了多种形状刚性容器内液体晃动的模态公式、波高公式和压力公式并详细介绍了液体晃动数值计算的有限体积(VOF)法。Fujita等[7]推导了环形柱体域内地震作用下液体线性晃动的频率、波高和压力分布公式，通过正弦三波试验验证了液体线性晃动的频率和波高结果，研究了液体深度和环形柱体域内外径比值对晃动频率、晃动波高和容器壁面压力的影响。Frano等[8]建立了XADS反应堆容器及堆内构件的简化三维有限元模型，采用ALE算法计算了地震作用下铅铋介质的晃动频率和晃动载荷，并进行了堆容器及堆内构件的屈曲分析以评价晃动载荷作用下的结构完整性。陈厚群等[9]于20世纪70～90年代对大型外浮顶储油罐的抗震试验开展了深入研究，提出了小变形范畴的动力相似准则，并基于此相似准则设计了储油罐缩尺模型，开展了该模型的正弦三波试验，进一步深入探讨了罐底翘离问题。中国实验快堆堆本体抗震试验[10-11]采用了结构弹性力和惯性力相似关系进行试验模型设计以考虑液体脉冲效应，并通过数值计算评价了相似关系引起重力失真的影响。

可见，目前常用于分析地震作用下堆本体流固耦合问题的三维有限元模型均大幅简化了堆本体结构，导致无法直接根据模型计算结果评价堆本体结构的完整性。既有试验研究采用的动力相似准则或仅满足液体晃动的相似关系，或仅满足堆本体结构地震响应的相似关系。为确保堆本体抗震试验中流体对流效应、脉冲效应和堆本体结构响应的准确性，保证重力、流体与固体惯性力、结构弹性力和结构应变的相似性，需发展更为适用的相似比模型，以更好地支撑堆本体的抗震试验研究。

在堆本体抗震试验中，为获得准确的流体对流效应，避免重力失真问题，同时获得准确的流体脉冲效应和堆本体结构响应，本文基于控制方程的量纲分析法，根据固体结构振动方程、流固界面边界条件和环形柱域液体晃动波高公式及压力分布公式[6]建立同时满足重力相似、流体与固体惯性力相似和结构弹性力相似的堆本体地震动力相似准则，并确保结构应变严格相似，以满足可能存在的堆本体失稳破坏相似要求。

1 相似关系推导

首先给出固体结构的振动方程：

(1)

式中：u为位移；ρ为密度；F为体力；θ为体应变；λ、G为拉梅常数；t为时间；下标s表示结构相关变量。

us=uxi+uyj+uzk

(2)

(3)

(4)

(5)

(6)

(7)

式中：ux、uy、uz为结构位移在x、y、z方向上的分量；i、j、k为x、y、z方向上的基矢量；E为结构材料的弹性模量；μ为结构材料的泊松比。

由式(1)～(3)可推导出无量纲表达式：

(8)

(9)

式中：L为几何尺寸；a为加速度。

不可压牛顿流体的动力学基本方程为：

(10)

式中：v为流体速度；ρf为流体密度；g为重力加速度；p为流体压强；ν为流体运动黏性系数。

v=vxi+vyj+vzk

(11)

p=pxi+pyj+pzk

(12)

式中：vx、vy、vz为流体速度在x、y、z方向上的分量；px、py、pz为流体压强在x、y、z方向上的分量。由此可得到4个无量纲表达式：

(13)

式中，下标f表示流体相关变量。

以上4个无量纲表达式分别代表流体的斯特劳哈尔数Sr、弗劳德数Fr、欧拉数Eu和雷诺数Re。

在流固交界面上满足：

-p=(σij)n=λθ+2Gεij

(14)

(15)

式中：σij为应力张量；εij为应变张量；vn为速度矢量；下标n表示流固界面的正法线方向。

可得无量纲表达式为：

(16)

(17)

由式(13)中π3和式(17)导出无量纲表达式：

(18)

由式(8)、(9)、(16)、(17)、(18)可推出如下独立相似关系：重力相似关系、固体与流体惯性力相似关系、弹性力相似关系以及雷诺数相似关系：

(19)

(20)

(21)

(22)

考虑到堆容器中液态金属钠正常运行温度下的黏度较小，故在计算其地震晃动波高时，可忽略流体的黏性，即模型流体与原型流体雷诺数相似的要求可放松。

选取模型尺寸L、时间t、流体密度ρ及重力加速度g为基本变量，获得地震作用下准确的堆本体液体晃动响应要求：

Sa=Sg=1

(23)

式中，S表示相似比。

同时为获得地震作用下准确的流体脉冲效应和堆本体结构响应，要求流体与固体惯性力、结构弹性力和结构应变严格相似，即：

(24)

(25)

(26)

式中，Sε为应变相似比。

将式(26)代入式(24)可获得流体与固体密度的相似关系：

(27)

将式(9)、(17)、(18)、(26)、(27)代入式(25)可得：

(28)

(29)

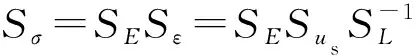
Sσ=SESε=SLSρSa

(30)

用分离变量法求解描述液体线性晃动问题的Laplace方程可得液体晃动的自振频率：

(31)

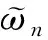
(32)

将式(23)代入式(32)可获得以下相似关系：

(33)

在地震作用下，堆本体内液体的晃动属于受迫振动。受简谐振动激励时，堆本体中具有自由液面的环形柱体域内液体晃动的波高公式为：

(34)

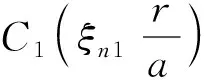
Sδ=Sus=SLf

(35)

简谐振动激励下液体晃动的压力公式为：

ρg(z-h)

(36)

式中，z为z轴坐标。由式(36)可得液体晃动压力的相似关系：

(37)

SpI=SρfSLSa

(38)

式中，pc、pI分别为动水压力和静水压力。

2 相似关系验证

为验证所选取相似准则的合理性与准确性，堆容器堆内构件验证模型的尺寸相似系数取为6，堆容器内液体计算模型的尺寸相似系数取为7，建立堆容器及堆内构件、堆容器内液体的缩尺模型，对堆容器堆内构件缩尺模型进行模态及反应谱分析。

2.1 堆容器堆内构件相似关系

验证计算中选取的主要相似系数列于表1，堆容器堆内构件计算模型如图1所示。

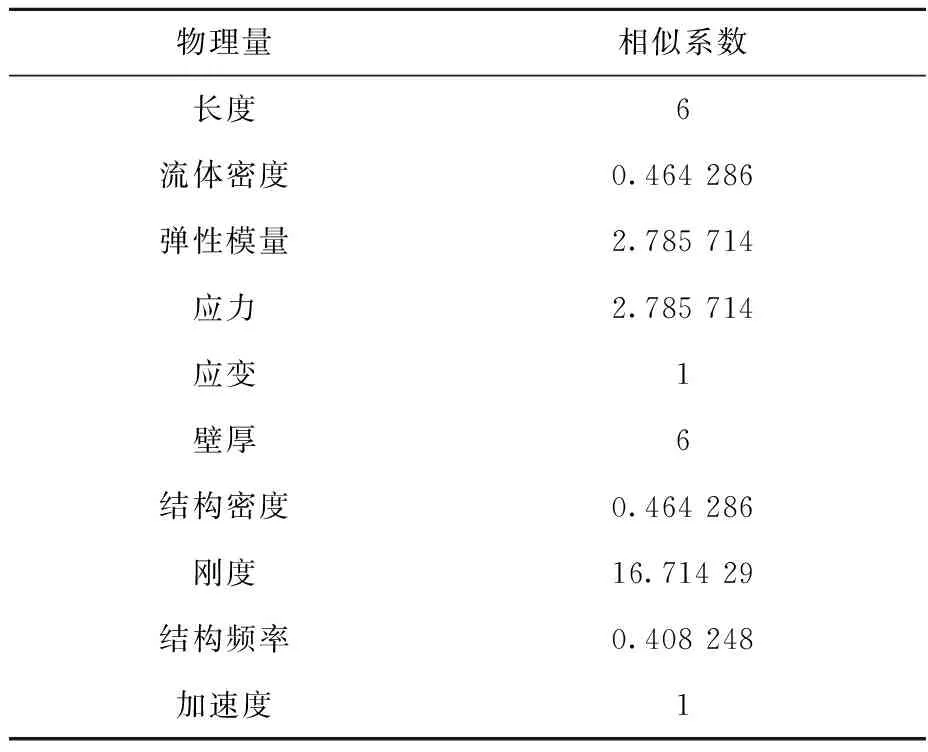
表1 结构相似系数Table 1 Structural similarity coefficient

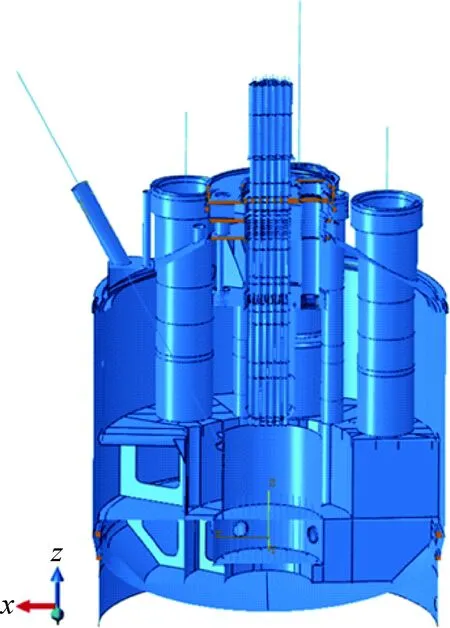
图1 堆容器堆内构件计算模型剖视图Fig.1 Section view of reactor vessel and reactor intervals computational model

2.2 堆容器内液体晃动相似关系

由于堆容器内具有自由液面的液体主要集中于由堆内支承上板、主容器筒体及堆内屏蔽外钢筒所围成的环形柱域内，因此堆容器内液体晃动相似验证采用简化模型。简化模型由内筒、外筒及底板组成，内外筒间为液体域，模型如图2所示，液体晃动验证计算中主要相似系数列于表2，计算模型尺寸列于表3，原型与缩尺模型的计算输入参数列于表4。

图2 堆容器内液体计算模型示意图Fig.2 Scheme of liquid computational model in reactor vessel

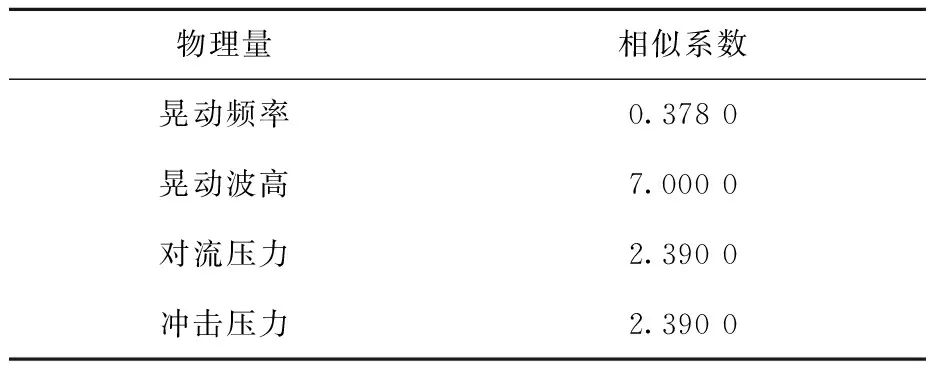
表2 液体晃动计算中的主要相似系数Table 2 Similarity coefficient in liquid sloshing calculation

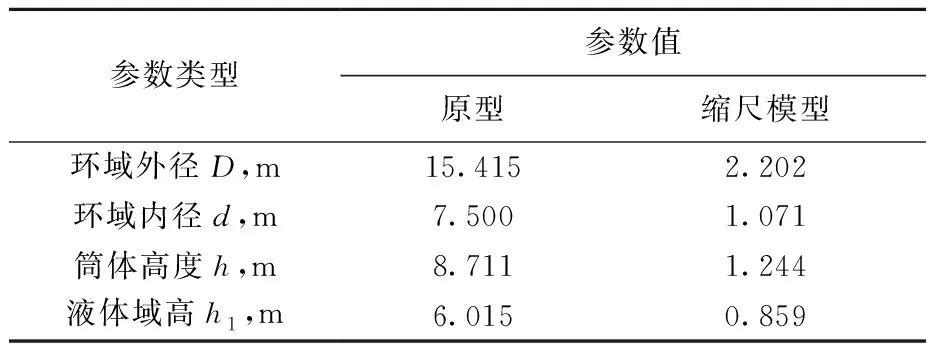
表3 液体晃动计算模型尺寸参数Table 3 Dimensional parameter of liquid sloshing computational model

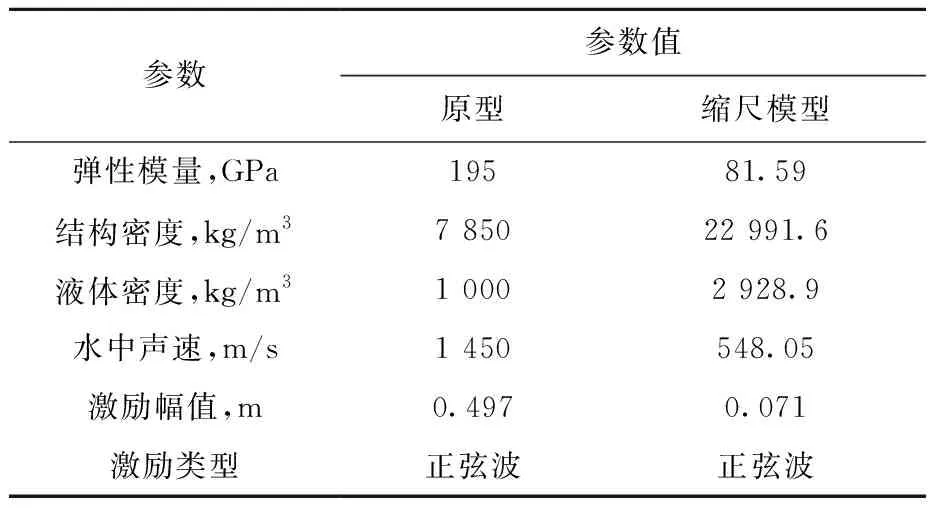
表4 液体晃动模型数值计算输入参数Table 4 Input parameter of liquid sloshing computational model

2.3 结果验证

2.3.1模态计算 在模态分析中，分别计算了原型与缩尺模型前1 100阶固有频率，两者总有效质量与模型总质量的比值均大于97.8%。原型与缩尺模型主要模态的计算结果列于表5。

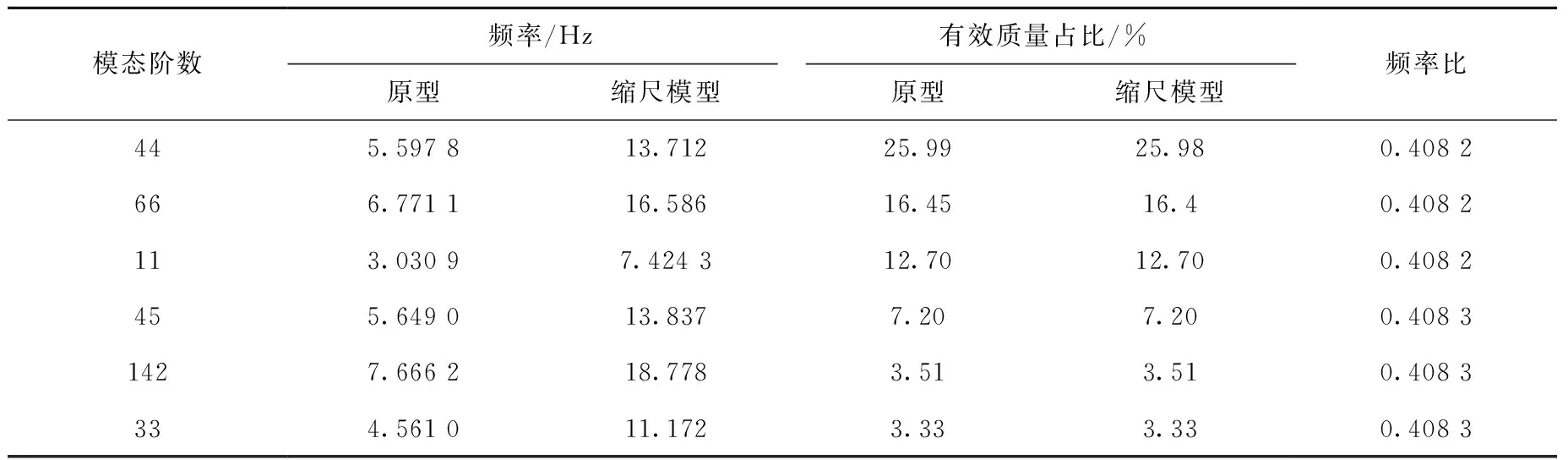
表5 原型与缩尺模型主要模态的计算结果Table 5 Calculation result of main modal of prototype and scaled model

由表5可看出，原型与缩尺模型的模态计算结果符合相似关系，且两者相同模态下有着基本一致的有效质量占比，使得计算结果可信度较高。原型与缩尺模型第11、44及66阶模态的振型对比示于图3。

a、c、e——原型；b、d、f——缩尺模型a、b——第11阶；c、d——第44阶；c、d——第66阶图3 原型与缩尺模型模态振型对比Fig.3 Modal comparison between prototype and scaled model

由原型与缩尺模型的模态振型对比可看出两者的振型一致。模型经过相似关系缩尺后，模态振型保持不变，频率按相似系数放大，由此可验证计算模型中所采用的相似准则满足动力相似的要求。

2.3.2谱分析 分别对原型和缩尺模型进行谱分析计算，得到谱分析计算结果。在谱分析中分别给出x、y和z3个方向上的加速度谱输入，计算结果按照平方和开平方(SRSS)方法进行叠加。缩尺模型的谱输入由原型中输入经过相似系数缩尺后得到。原型与缩尺模型地震响应结果对比列于表6。可见，原型与缩尺模型的Tresca应力比基本上保持在2.785左右，与相似关系中的应力相似系数Sσ=2.785 714相一致。由此可以得出缩尺模型谱分析结果与原型相比满足动力相似关系的要求。

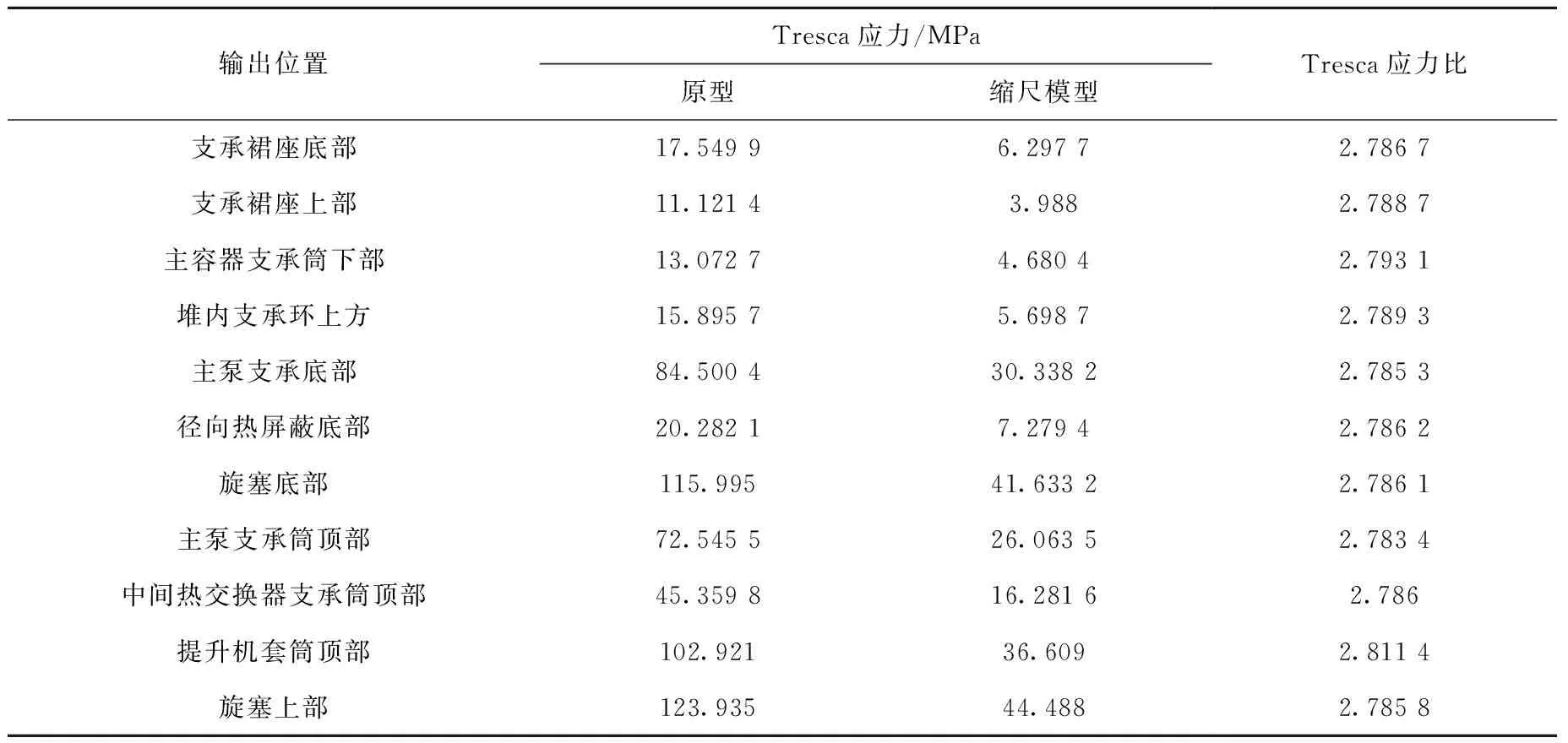
表6 原型与缩尺模型谱分析的Tresca应力对比Table 6 Tresca stress comparison between prototype and scaled model

2.3.3液体晃动固有频率 缩尺模型计算得到的液体1阶、2阶固有频率如图4所示，原型与缩尺模型液体晃动频率计算结果列于表7。

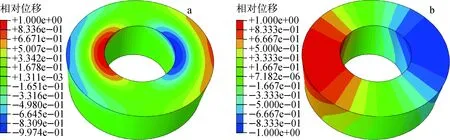
图4 缩尺模型液体1阶(a)、2阶(b)晃动频率Fig.4 First (a) and second (b) liquid sloshing frequencies of scaled model

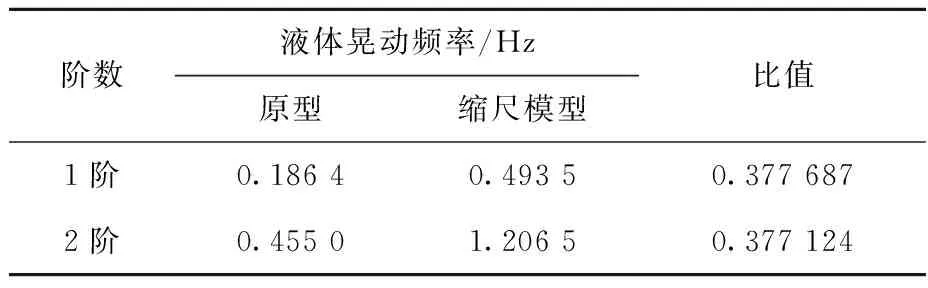
表7 液体晃动频率Table 7 Liquid sloshing frequency

根据计算结果，数值计算得到的液体晃动固有频率比值与通过相似准则计算得到的相似系数的差异分别为0.072%、0.222%，所选取液体晃动固有频率相似准则合理。

2.3.4液体晃动波高 进行液体晃动固有频率、液体晃动波高、液动压力、液体晃动对支承处的倾覆力及倾覆力矩的数值计算中，相应的材料及边界参数均与表4一致，原型、缩尺模型施加的正弦波激励频率分别为0.186 4 Hz、0.493 5 Hz，两种模型的计算总时长均为5个周期，获得的液体晃动波高如图5所示。

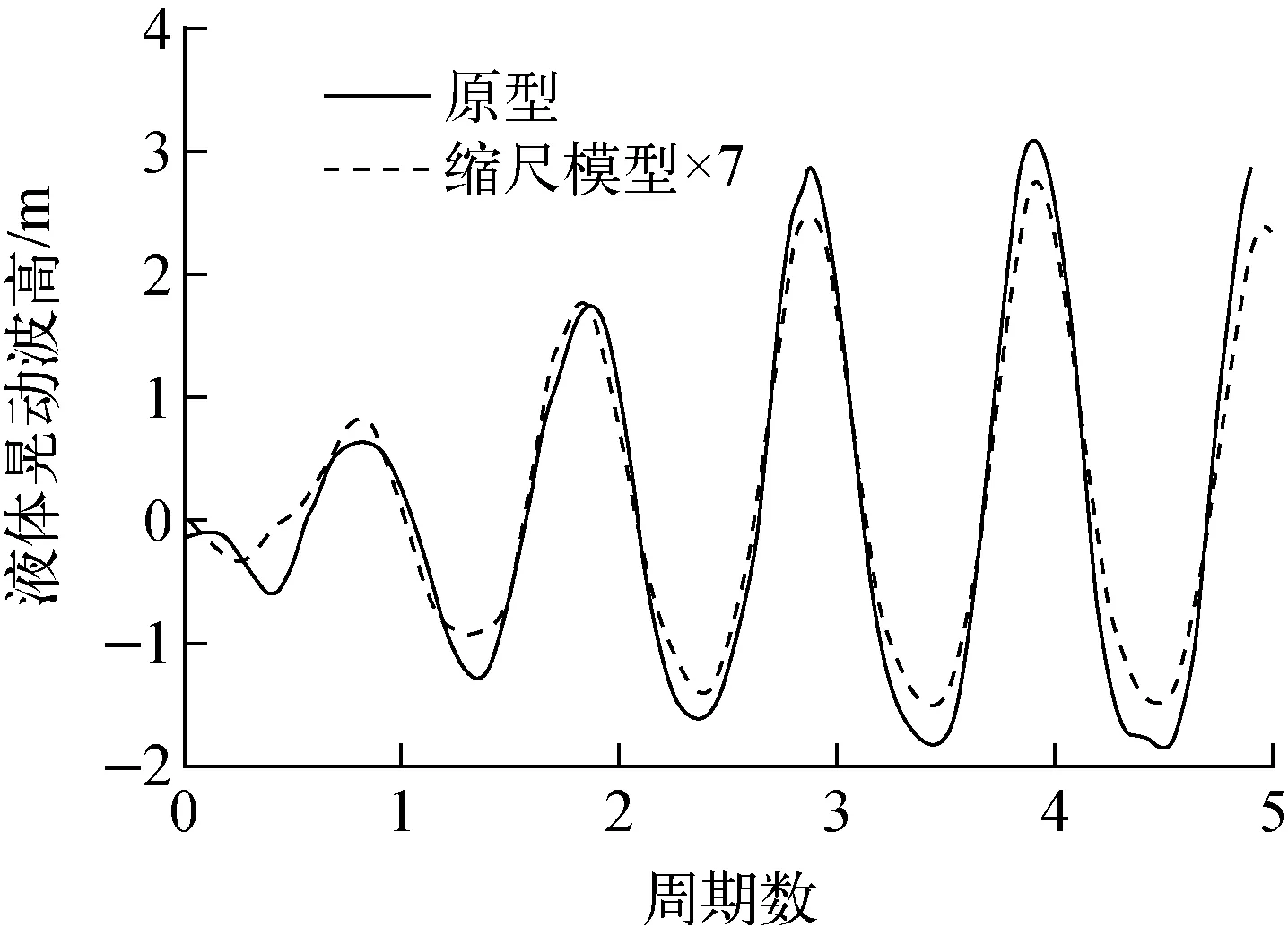
图5 原型及缩尺模型液体晃动波高Fig.5 Liquid sloshing height of prototype and scaled model

根据计算结果，缩尺模型液体晃动波高乘以相似系数7得到的波高曲线与原型波高曲线整体趋势及波动范围均有较好的一致性，由此可判断波高相似准则应用于液体晃动问题是合理的。

2.3.5支座反力及力矩 液体晃动问题关心的是液体在晃动过程中对容器根部产生的倾覆力矩，对比分析中提取在5个周期不同时刻容器底部中心处参考点的倾覆力矩，原型与缩尺模型支座裙的倾覆力矩如图6所示。

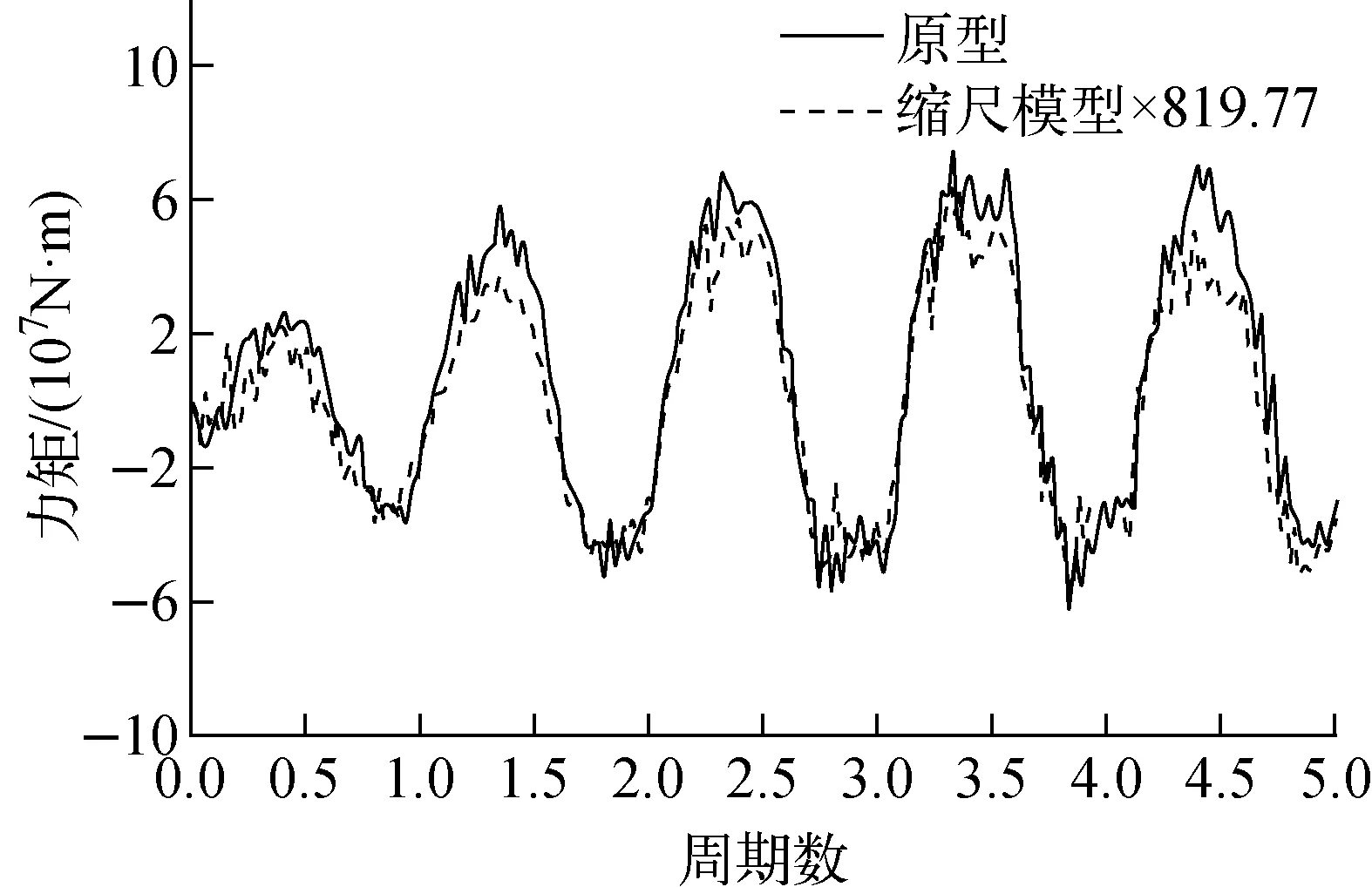
图6 原型及缩尺模型的倾覆力矩Fig.6 Overturning moment of prototype and scaled model

缩尺模型倾覆力矩乘以相似系数819.77得到的力矩-时间曲线与原型的整体趋势及力矩有较好的一致性，可判断倾覆力矩的相似系数应用于液体晃动问题是合理的。

2.4 试验模型设计应用

根据相似关系要求，试验样机模型结构密度应为原型结构密度的2.93倍。为满足相似关系对试验样机质量的要求，采用人工附加质量的方式补足试验样机重力及惯性力效应，试验样机设计拟采用铅和碳钢作为人工附加质量材料，采用配重板的形式将附加质量施加在样机结构上，并通过调整配重板与样机结构的连接形式以降低附加质量对样机结构刚度的影响，配重板布置示于图7。

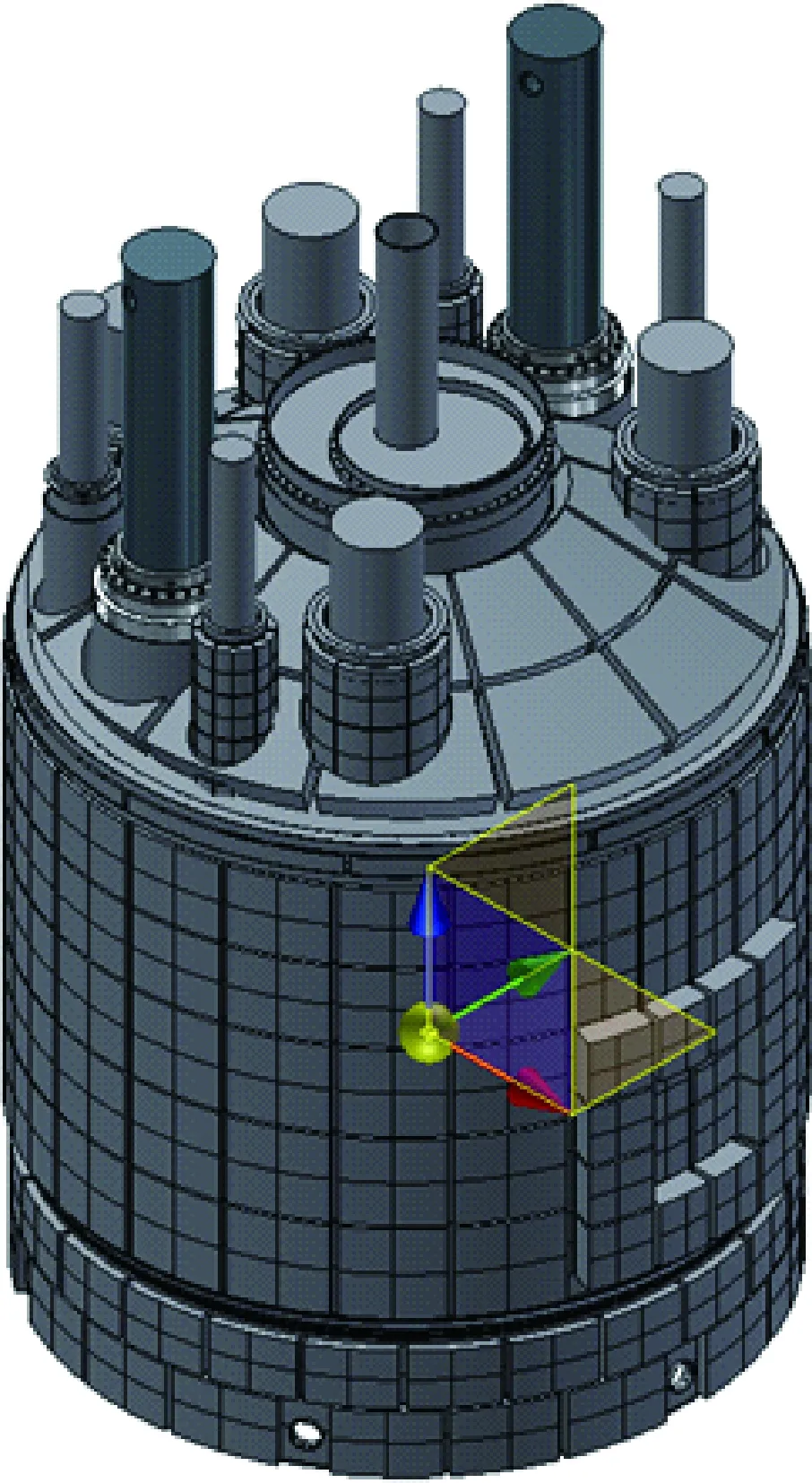
图7 缩尺模型配重板布置图Fig.7 Layout plan for clump weight on scaled model

3 结论

本文采用不同的相似系数分别对堆本体抗震试验中所用到的堆容器堆内构件结构及液体晃动问题的相似关系进行了验证计算。根据相似关系的验证结果可得到如下结论。

1) 通过比例模型的分析计算验证了相似关系的合理性和准确性。

2) 按照本文提出的相似准则设计试验样机可准确计入液体晃动效应并反映真实堆本体模型的动力特性及动力学响应。

3) 堆容器堆内构件和堆容器内液体按照相似准则进行缩尺后，可通过缩尺模型的抗震试验进一步验证本文的相似关系。