回填工况下地下粮仓的摩擦力分析

2021-06-30刘海燕徐向楠张昊王振清杨金平马天鹤

现代食品科技 2021年6期

刘海燕，徐向楠，张昊，王振清，杨金平，马天鹤

（河南工业大学土木工程学院，河南郑州 450001）

自古以来中国的粮食问题都是影响社会发展的重要因素，如今确保粮食安全也是中国的农业政策之一[1,2]，中国粮食库存量达0.4亿t，其中高大平房仓仓容占总仓容的87.5%[3]。但其需要环流熏蒸灭虫菌[4]、空调降温[5]等处理使得高大平房仓高有耗能、高成本、易污染、等缺点。而地下粮仓作为拥有悠久历史[6,7]且具有高隐蔽性[8]、自然低温、恒温、环保绿色、节能节地、机械化操作、可长期储存[9,10]等优良特点。在地下粮仓向高水位地区推广时必然面临地下水浮力这一不同于地上粮仓的新因素的影响[11]。当前地下结构的抗浮设计多以阿基米德定律为基础，再辅以配重法、支护锚杆法、抗拔桩法等方法进行建筑结构抗浮设计，但地下粮仓所属环境并非纯水环境，而阿基米德定律适用于部分或全部浸入密度一致流体的物体，如何考虑地下粮仓在周围土体或者在地下粮仓开挖后回填工况下产生的摩擦力的影响具有一定工程意义。

地下结构受地下水作用的浮力影响方面，国内外学者进行了大量研究。刘海燕[12]等通过模型筒试验认为回填工况地下粮仓在预警水位时实际抵抗浮力为理论抵抗浮力的1.5倍，实际起浮水位时抵抗浮力为理论抵抗浮力的2倍。梅国雄[13,14]试验得出在黏土中地下水的浮力折减系数可达0.7，同时还提出了在抗浮原则上提出了以均布抗拔力平衡均布水浮力的观点。倪伟杰[15]通过试验反映了在强度很低的回填软土中实测浮力明显大于水浮力这是事实并提出了相应的浮力计算公式。金立兵[16]通过现场试验研究与理论分析相结合的方法认为给出了仓体所受实际浮力与理论浮力有差距并给出了线性表达式。梁妍妍[17]概述了地下水的赋存状态、渗流、地下筒壁摩阻力、抗浮设防水位对浮力计算的影响。D. A. Dixon[18]通过压实伊利石、钠基膨润土和砂的低梯度试验认为密度高的土体具有较高的水体梯度承受能力。Boonchai Ukritchon[19]研究地下洞室的不排水稳定性平面应变下的二维有限元极限，提出了不排水地下洞室，线性改变其黏土强度时的稳定性计算方程。Eimar Sandoval[20]认为对于在饱和土壤中的柔性隧道，在地震时随着其周围土体超空隙水压的增大，会发生绝对变形从而增加其抗震性。D. J.RICHARDS[21]通过长期的现场监测证实，透水挡土墙的孔隙水压力远低于类似土壤中不透水挡土墙的预期压力。Jikai Zhou[22]等人通过试验表明水位一只时改变地下室的埋置深度，其所受的浮力不一致，同时给出了通过阿基米德原理计算的浮力与实际测量浮力之间的折减系数在0.25~0.52之间。

由上可知地下结构受到的地下水的浮力并不等于由阿基米德原理计算的浮力，摩擦力也是造成该结果的原因之一。关于摩擦力，国内外相关学者进行了大量研究。15世纪，摩擦力出现在了达芬奇的笔记本上，18世纪，库伦定律诞生了，它描述了简单的机械摩擦的基本规律，17世纪牛顿提出了内摩擦定律，指出了液体之间也存在摩擦力。今天，摩擦消耗掉全世界1/3的一次性能源，在中国，每年因摩擦磨损造成的损失占中国国民生产总值的4.5%[23]。当然摩擦力带来的不只有坏处，在地下结构的抗浮设计中，其就是有利因素。按照《给水排水工程构筑物结构设计规范》[24]，结构侧壁摩擦力作为抗浮的有利因素可以更好地保证地下结构的安全性，故不考虑在抗浮设计的荷载计算中。李帅[25]等人通过工程实例验证认为大中直径桩的负摩阻力计算依据《建筑桩基技术规范》[26]取值是合理的。王永璐[27]等人发现，土体黏聚力与土体内摩擦角随含水率的增大表现出相反的变化规律。孙文[28]等人通过试验发现湿陷性黄土与混凝土接触面存在滑移破坏和弹塑性破坏，接触面粗糙度不同时，接触面的抗剪强度峰值也不同，接触面越粗糙，其黏聚力也越大，内摩擦角越小。柳涛[29]认为在应变一定时，土体的动剪切模量随着纤维掺入量以及含水率的增大先增大后减小。龙昊鹏[30]从桩—土相对位移出发分析了桩基负摩阻力产生的机理同时结合《建筑桩基技术规范》提出了检测标准。刘明[31]基于荷载传递理论，选取佐藤悟双折线函数作为桩侧土与桩端土的荷载传递模型，建立了桩侧桩端阻力双折线式能量法。对新近深厚填土桩基负摩阻力进行了定量计算和特性分析。Hong-quan Li[32]等通过ABAQUS软件，将桩土界面的弹性-粘塑性界面本构模型开发到FRIC子程序中，对桩侧摩阻力和桩土相对位移进行了较贴合实际的模拟计算。

该文以二八灰土回填工况的地下粮仓（图1）为背景，设计了3个材质、仓底倾角相同，直径分别为400 mm、500 mm、600 mm的模型筒仓A、B、C，按照仓底、仓壁均回填二八灰土的工况a和仓壁回填二八灰土、仓底采用砂土的工况b两种回填工况，对模型筒仓进行了6组注水试验，探讨回填工况下地下粮仓在地下水作用时的摩擦力变化情况。通过该文，提出在地下水作用下，地下粮仓抗浮设计中摩擦力的计算方法，为今后地下粮仓及其它地下结构的抗浮设计提供参考。

图1 模型筒仓建设图Fig.1 Underground silo construction drawing

1 地下粮仓理论力学模型

在地下水的作用下，地下粮仓不仅受到地下水的浮力作用，同时也受到周围回填土的作用力。在地下粮仓起浮之前即静止阶段，将地下粮仓受到的由土体产生的阻碍地下粮仓上浮的力（如粘滞力、孔隙水压力等）均视为地下粮仓受到的静摩擦力F摩静；上浮阶段受到的摩擦力记为F摩动。考虑实际回填工况，静止阶段地下粮仓的力学模型见图2，上浮阶段地下粮仓的力学模型见图3。

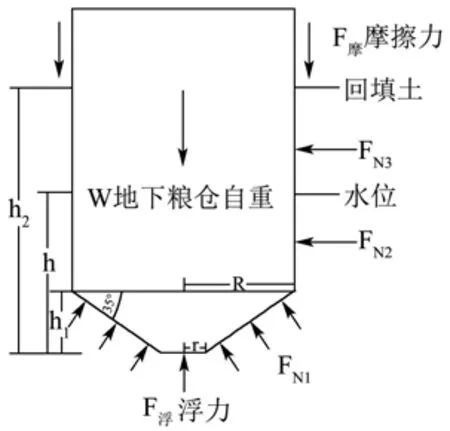
图2 静止阶段地下粮仓浮力力学模型Fig.2 Mechanical model of buoyancy of underground granary in static friction stage

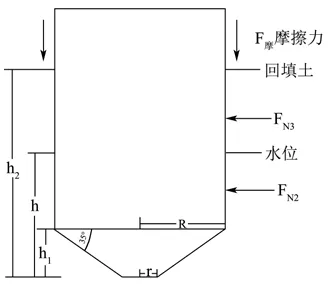
图3 上浮阶段地下粮仓浮力力学模型Fig.3 The buoyancy mechanics model of underground granary in sliding friction stage

1.1 静止阶段地下粮仓力学模型

静止阶段，竖直方向上，地下粮仓受到自重W、静摩擦力F摩静、土体支承力F土、浮力F浮的共同作用。

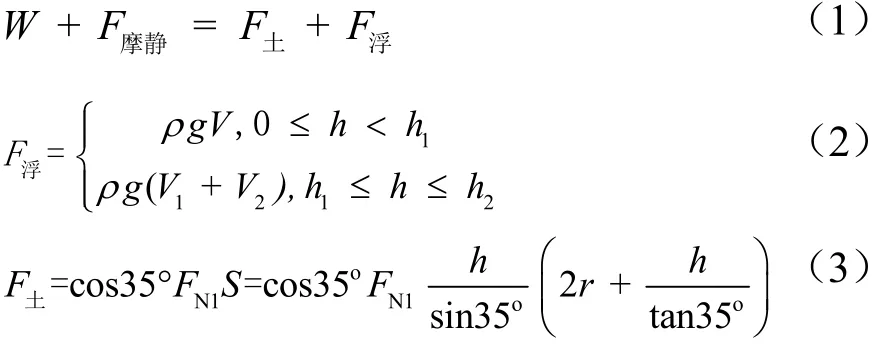
式中：W为地下粮仓自重，N；F浮为模型筒仓受到的浮力，N；ρ为水的密度取（103kg/m3）；g为重力加速度（9.8 N/kg）；V为模型筒排开水的体积，m3；h为水位高度，m；h1为仓底高度，m；V1为仓底体积，m3；V2为随水位升高地下粮仓仓壁部分排开水的体积，m3；FN1为仓底周围土体产生的垂直于仓底侧面的均布土压力，N；S为仓底与土体接触面在竖直方向上的投影面积，m2；r为仓底下底圆半径。

1.2 上浮阶段地下粮仓力学模型

上浮阶段，地下粮仓所受的动摩擦力F摩动为

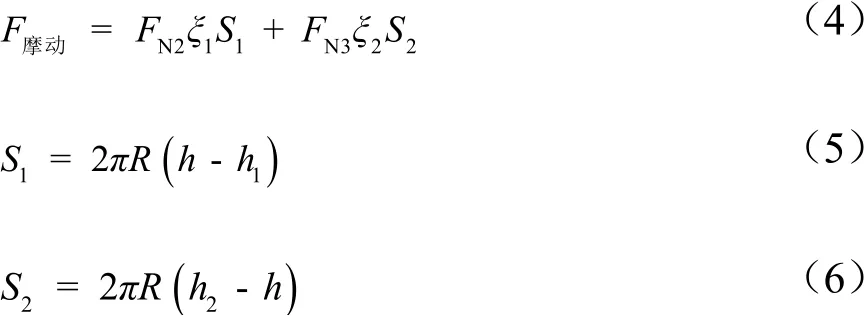
式中：F摩动为上浮阶段地下粮仓受到的动摩擦力，N；FN2为地下粮仓水位以下部分土产生的垂直于地下粮仓仓壁的均布侧压力，N；FN3为水位以上回填土面以下部分土产生的垂直于地下粮仓的均布侧压力，N；S1为仓壁部分水面以下面积，m2；S2为仓壁部分水面以上，覆土高度以下面积，m2；ξ1，ξ2为摩阻力系数，参考《建筑桩基技术规范》取值，ξ1取0.25、ξ2取0.4。

2 模型试验

该文以二八灰土回填工况的地下粮仓为背景，设计了3个材质、仓底倾角相同，直径分别为400 mm、500 mm、600 mm的模型筒仓A、B、C，按照仓底、仓壁均回填二八灰土的工况a和仓壁回填二八灰土、仓底采用砂土的工况b两种回填工况，对模型筒仓进行了6组注水（普通自来水）试验，探讨回填工况下地下粮仓在地下水作用时的摩擦力变化情况。

2.1 试验设备

该试验用到的试验设备主要有四部分组成，试验装置见图4。尺寸为2000 mm×2000 mm×1000 mm的模型池、固定横梁、固定平台等固定装置。直径分别为400 mm、500 mm、600 mm的模型筒仓A、B、C，其外表面涂刷水泥浆，参数见表1。长度为3 m，精度为1 mm的直尺，用以测量水位的变化情况；2组量程为±100 mm，精度为1 mm的位移计，固定于模型池顶部横梁上，用于监测模型筒仓的位移；4组8个量程为0.3 MPa，精度≤0.05%的压力传感器，其中2组4个对称粘贴于仓底圆台母线三等分点处，另外2组4个在仓壁周围自下而上对称粘贴于1000 mm、3000 mm处（见图5），用以仓底、仓壁周围的水土压力；量程为200 kg,精度为0.25%的压力盒，测量仓顶所受支反力。水管、木板等辅助设备。

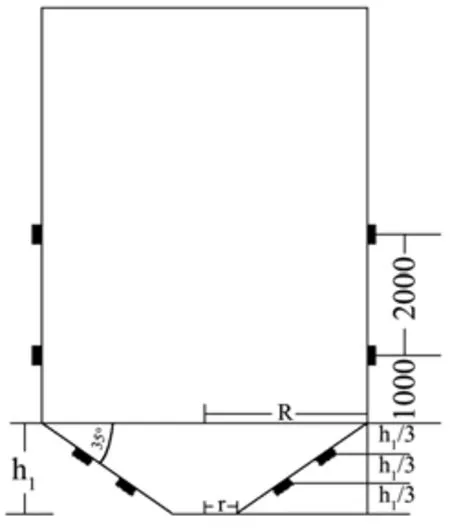
图5 压力传感器布置图Fig.5 Pressure sensor layout

表1 模型筒仓参数表Table 1 Table of model silo parameters

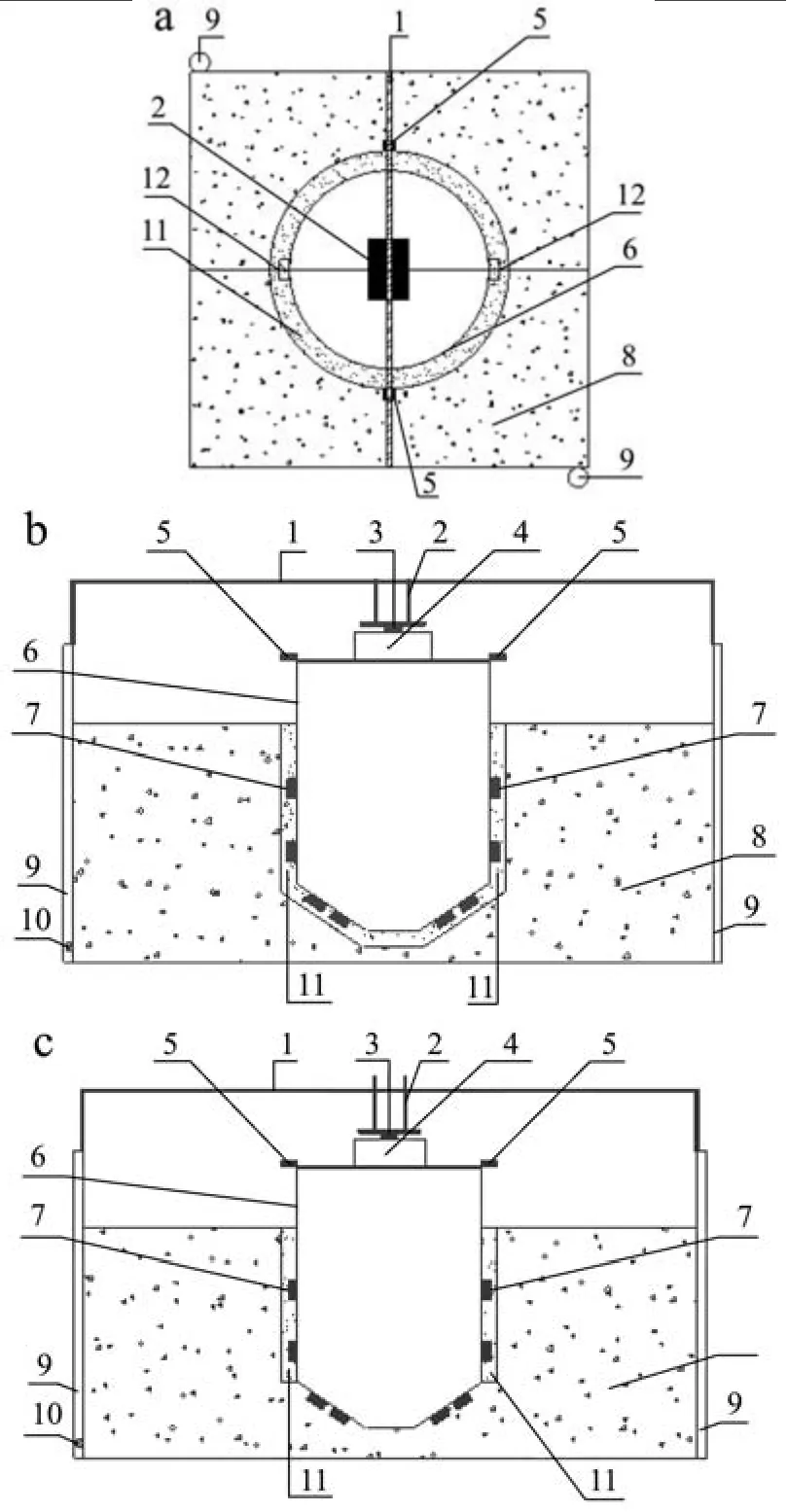
图4 试验装置图Fig.4 Test device diagram

2.2 试验步骤

第一步，制作一个尺寸为2000 mm×2000 mm×1000 mm的模型池，在距池底20 mm处设置一排水口，在池内对角设置两根水位管以测量水位，玻璃池上端置一固定横梁以便安置试验仪器。第二步，底部铺设一定厚度的粗砂，在粗砂内埋设一每隔50 mm扎一对小孔的塑料管。第三步，放置模型筒仓，工况a情况下，在模型筒仓仓壁周边及仓底200 mm范围内回填二八灰土，其余位置均填入粗砂；工况b情况下，在模型筒仓仓壁周边200 mm范围内回填二八灰土，仓底及其余位置均回填粗砂。第四步，安放模型筒仓仓顶2组位移计及压力盒。第五步，连接模型筒仓仓底、仓壁压力传感器，仓顶压力盒，位移计至DH3821应变测试仪和计算机，调试归零各试验设备。第六步，缓慢注水，2 min测量一次水位，至模型筒仓上浮至模型筒仓倾覆，见图6，试验结束。

图6 注水试验结束图Fig.6 End drawing of water injection test

2.3 试验受力分析模型

由于固定横梁的存在，模型筒仓受到了竖直向下的支反力F支反，模型筒仓力学模型见图7。静止阶段，模型筒仓的摩擦力为

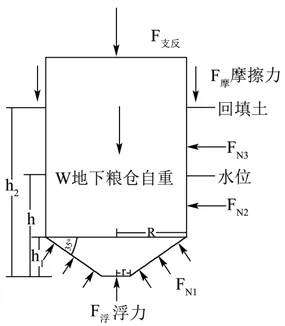
图7 模型筒仓力学模型Fig.7 Model silo mechanics mode

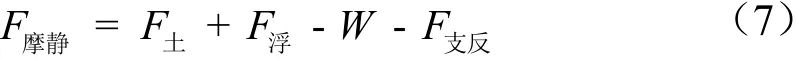
式中，F支反是模型筒仓上浮时受到的上部横梁提供的支反力，N。上浮阶段，模型筒仓受到的动摩擦力计算公式同公式（4）。

3 结果与分析

3.1 水位与位移计读数关系分析

根据测量水位与位移计读数，绘制模型筒仓A、B、C的水位-位移曲线见图8，并由图8将模型筒仓初始采集水位、位移突变点水位、注水结束水位及其各自对应的位移绘制水位-位移表2。

经表2分析可知：

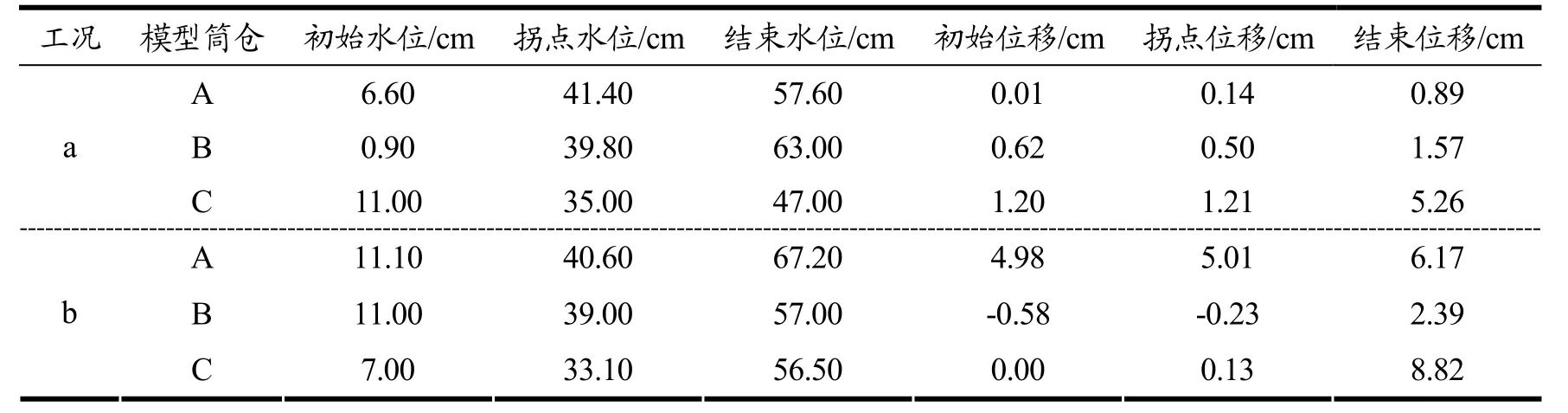
表2 水位-位移表Table 2 Water level-displacement table

（1）图8中，模型筒仓位移先减小后基本稳定，原因是注水后土体产生固结所致。

（2）图8中，模型筒仓固结稳定后分为静止、上浮两个阶段。在静止阶段，模型筒仓A、B、C顶部位移计读数稳定于初始值；在上浮阶段，模型筒仓顶部位移计数据发生突变，工况a时，模型筒仓A、B、C水位-位移曲线拐点处斜率分别由0变为0.01、0.12、0.01，工况b时，模型筒仓A、B、C水位-位移曲线拐点处斜率分别由0变为0.01、0.04、0.04，说明模型筒仓在水位达到起浮点时，迅速浮起。

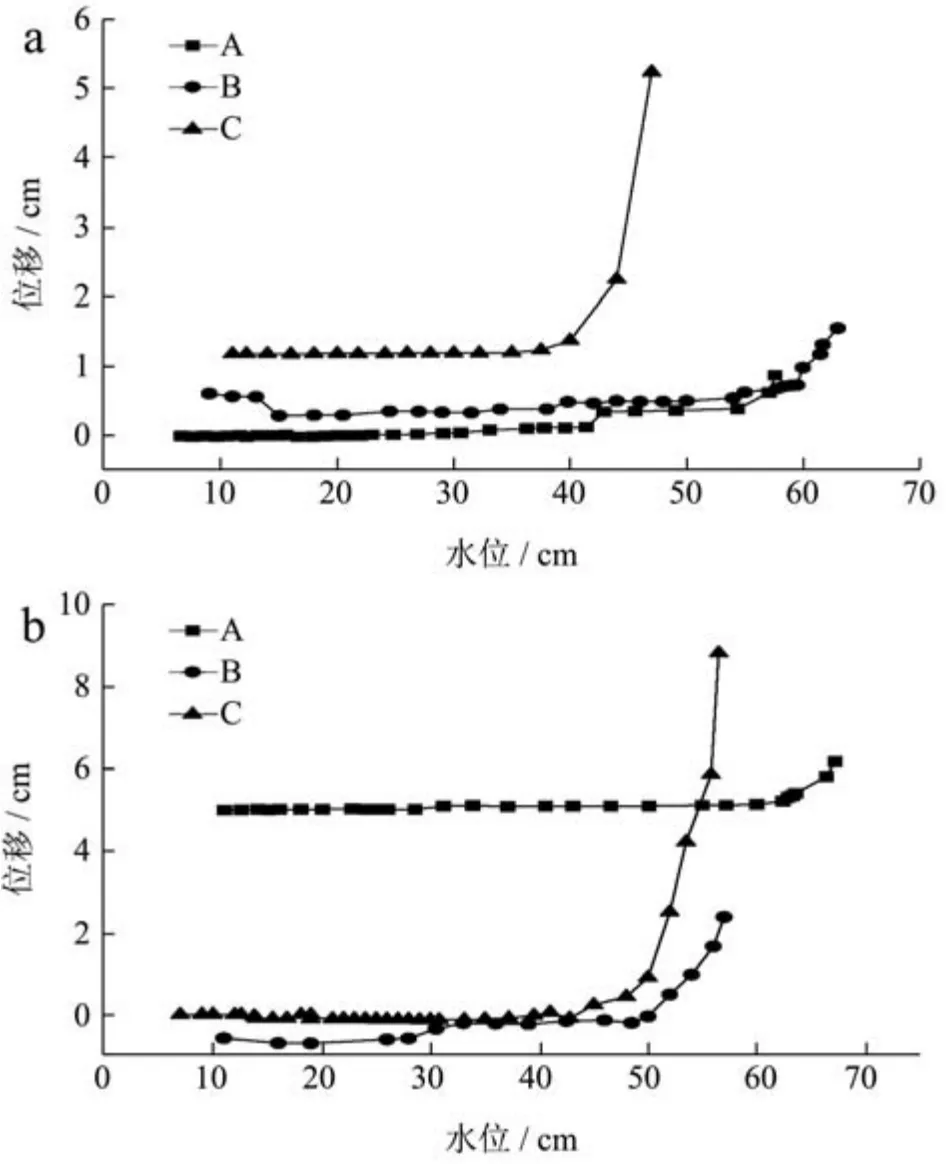
图8 模型筒仓A、B、C的水位-位移曲线图Fig.8 Water level-displacement curve of model cylinder A, B, C

（3）在静止阶段，工况a时，模型筒仓A、B、C的起浮水位分别为41.40 cm、39.80 cm、35.00 cm，工况b时，模型筒仓A、B、C在工况b中的起浮水位分别为40.60 cm、39.00 cm、33.10 cm；结合表1中模型筒仓周围填土高度（覆土高度，与表1中描述一致），分析可知仓底回填二八灰土的工况a比仓底采用粗砂的工况b具有更好的抗浮能力。

（4）在上浮阶段，工况a、工况b中，模型筒仓A、B、C位移-水位曲线随水位上升的曲线趋势一致。

3.2 水位与支反力关系分析

跟据测量水位与顶部压力盒测得的支反力，绘制模型筒仓A、B、C的水位-支反力曲线见图9，并由图9将模型筒仓初始采集水位、支反力突变点水位、注水结束水位及其各自对应的支反力绘制水位-支反力表3。

经表3分析可知：

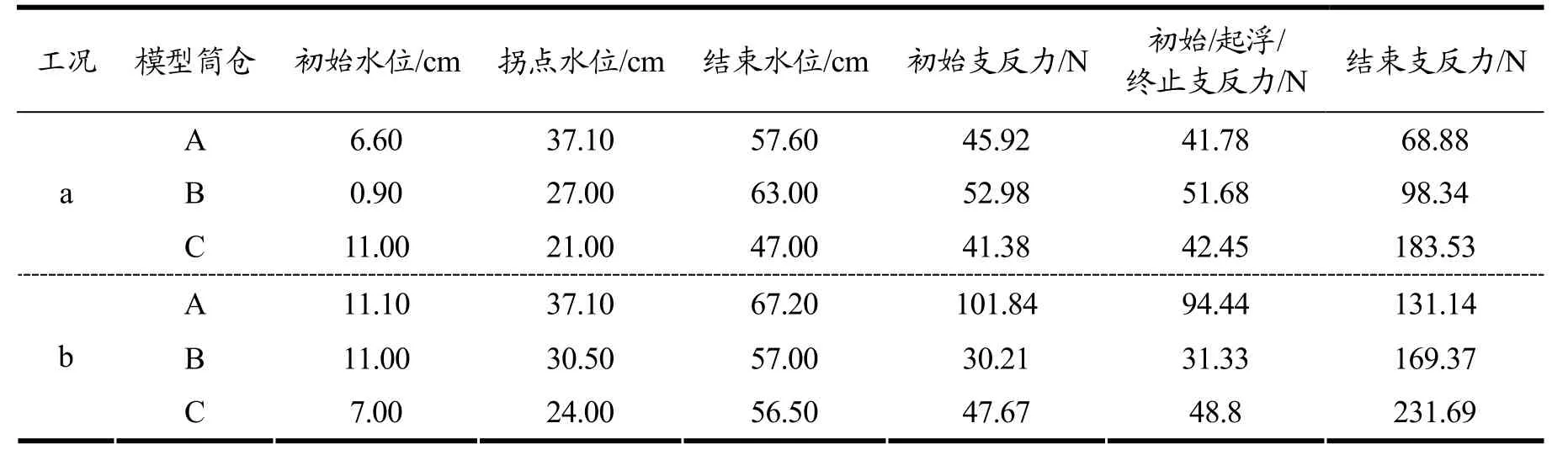
表3 水位-支反力表Table 3 Water level-side reaction table

（1）由图9可知，模型筒仓支反力先减小后基本稳定，原因是注水后土体产生固结所致，与位移变化规律一致。

（2）由图9可知，模型筒仓固结稳定后分为静止、上浮两个阶段。在静止阶段，模型筒仓A、B、C顶部位压力盒监测的支反力读数基本不变，在上浮阶段，模型筒仓顶部压力盒监测的支反力数据发生突变，工况a时，模型筒仓A、B、C水位-支反力曲线拐点处斜率分别由0变为0.11、0.27、0.53，工况b时，模型筒仓A、B、C水位-支反力曲线拐点处斜率分别由0变为0.49、0.12、0.25，说明模型筒仓在水位达到起浮点时，迅速浮起。

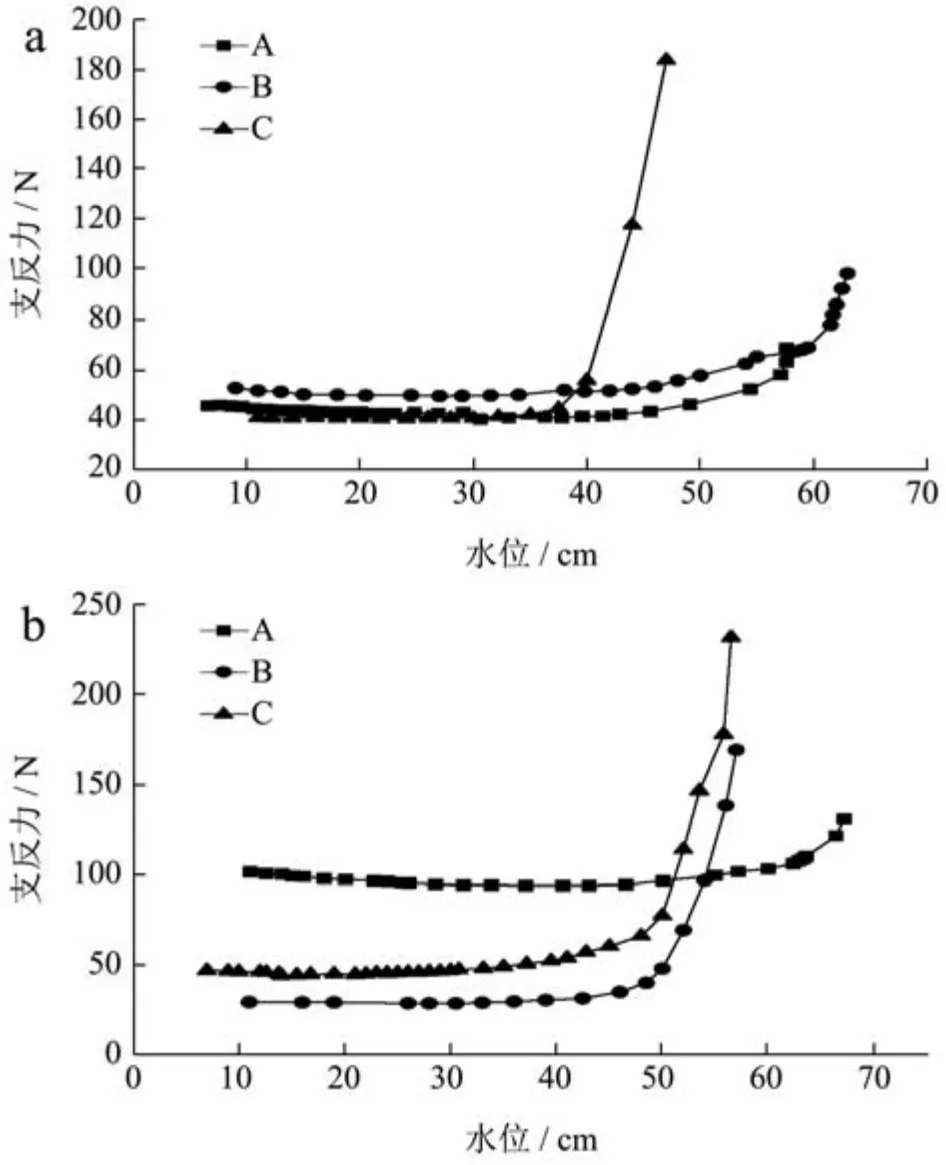
图9 模型筒仓A、B、C的水位-支反力曲线图Fig.9 Water level-branch reaction curve of model silo A, B, C

（3）在静止阶段，支反力基本保持不变。模型筒仓A、B、C在工况a中的支反力拐点对应的水位分别为37.10 cm、27.00 cm、21.00 cm，模型筒仓A、B、C在工况b中的支反力拐点对应的水位分别为37.10 cm、30.50 cm、24.00 cm，水位-支反力曲线的拐点水位均小于水位-位移曲线的拐点水位，说明静摩擦力的存在造成了位移的变化滞后于支反力的变化。

（4）在上浮阶段，工况a、工况b中，模型筒仓A、B、C支反力-水位曲线随水位上升的曲线趋势一致。

3.3 水位与摩擦力关系分析

根据测量水位与试验采集的仓底、仓壁压力传感器的读数，利用公式（7）计算静摩擦力，利用公式（4）计算滑动摩擦力，绘制模型筒A、B、C的水位-静摩擦力曲线，根据图10，结合模型筒仓的试验参数，绘制摩擦力分析表4。

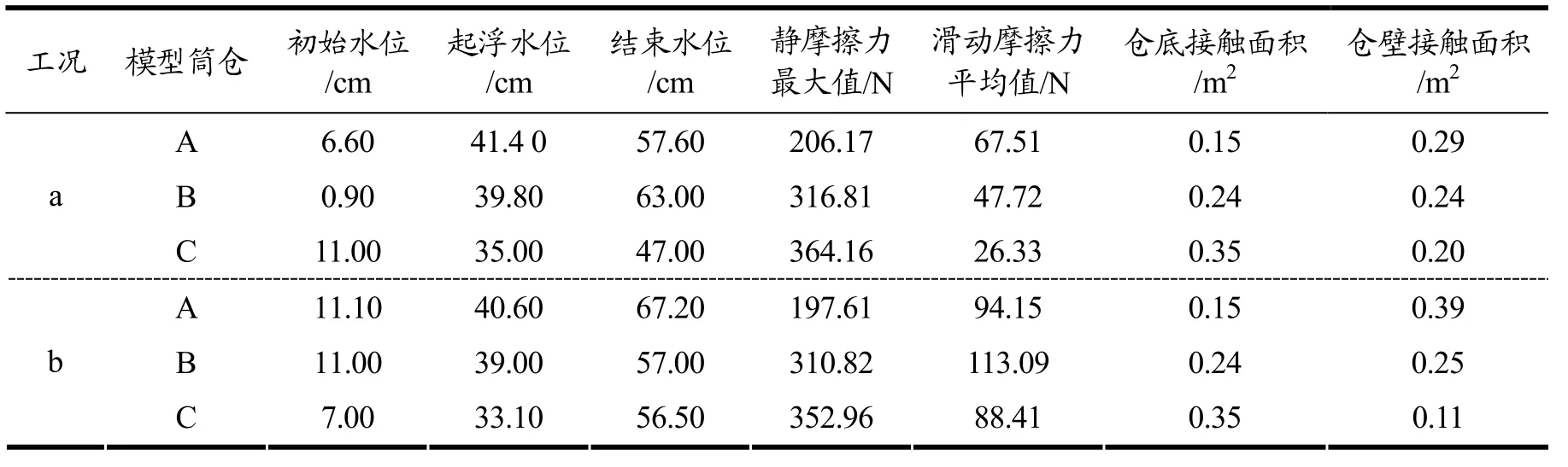
表4 摩擦力分析表Table 4 Friction analysis table

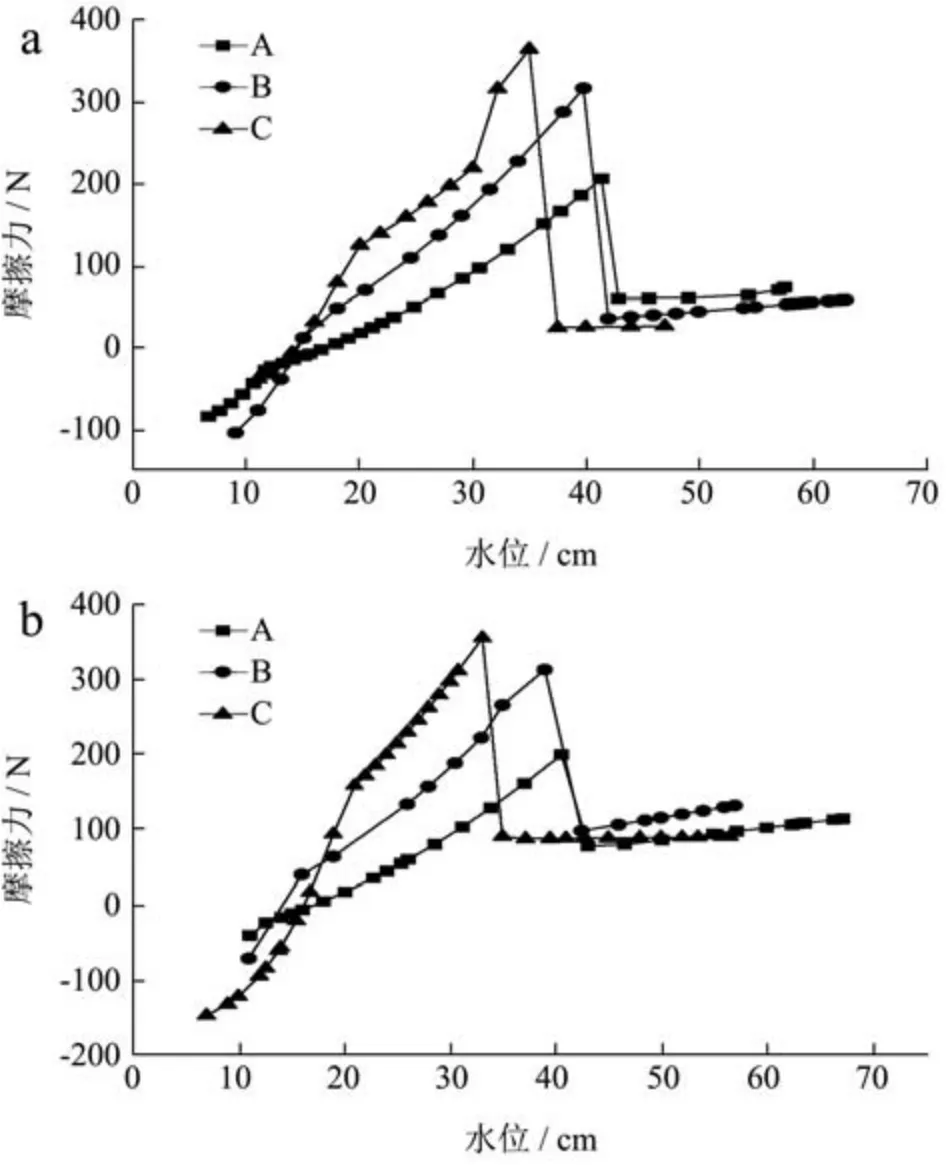
图10 模型筒仓A、B、C的水位-摩擦力曲线图Fig.10 Model silo water level- friction curves of model silos A, B,C

经表4分析可知，

（1）模型筒仓A、B、C在工况a、b中均存在静止和上浮两个阶段。

（2）在静止阶段，模型筒仓所受的摩擦力为静摩擦力，工况a、工况b的静摩擦力均随水位上升而逐渐增大；工况a时，模型筒仓A、B、C所受的静摩擦力随水位上升1 cm的增大幅度分别为4.98 N、7.96 N和10.40 N，工况b时，模型筒仓A、B、C所受的静摩擦力随水位上升1 cm的增大幅度分别为4.88 N、7.97 N和10.66 N。说明工况对静摩擦阶段摩擦力随水位的上升幅度无影响。

（3）在上浮阶段，模型筒仓所受的摩擦力为动摩擦力，工况a、工况b的动摩擦力均迅速下降并趋于稳定。

（4）在静止阶段，由图10可知，工况a时，模型筒仓A、B、C对应的最大静摩擦力分别为206.17 N、316.81 N、364.16 N；工况b时，模型筒仓A、B、C对应的最大静摩擦力分别为197.61 N、310.82 N、352.96 N。由表1可知，工况a中模型筒仓A、B、C的覆土高度分别为450 mm、410 mm、410 mm，工况b中模型筒仓A、B、C的覆土高度分别为460 mm、420 mm、360 mm，说明仓底回填二八灰土的工况a比仓底采用粗砂的工况b具有更好的抗浮能力。

（5）在上浮阶段，模型筒仓A、B、C在工况a中的平均动摩擦力分别为65.71 N、47.72 N、26.33 N；模型筒仓A、B、C在工况b中的平均动摩擦力分别为94.15 N、113.09 N、88.41 N。

（6）模型筒仓A、B、C在工况a和工况b中动摩擦力均小于最大静摩擦力，在实际工程的抗浮设计中由于静摩擦无法直接计算，采用动摩擦力计算是安全可靠的。