高等数学中空间曲线切线求法的探讨

张俊强 毕金龙 胡澳欣 苟乔笙

〈中国矿业大学（北京）理学院 北京 100083〉

众所周知，高等数学是高校理工科专业学生第一年的一门必修课。由于该课程内容多且难度大，因此大部分教材将其分成上下两册进行两学期讲授。以同济大学数学系编的《高等数学》[1]为例，下册主要包括向量与空间解析几何，多元函数微分学，重积分，曲线和曲面积分，无穷级数等内容。其中空间解析几何部分主要介绍了空间的直线，平面，曲线和曲面的性质。在介绍完多元函数的微分学之后，以此作为研究工具，课本介绍了空间曲线切线和法平面以及空间曲面的切平面及法线的求法。学生在学习这部分内容时，往往感到概念公式繁多、计算复杂、缺少几何直观等，这是造成学生学习困难的主要原因。

别一方面，十七世纪，著名的捷克教育学家夸美纽斯在他的著作《大教学论》中首次提出了“直观教学”的思想并主张将“直观性”作为一项基本教育原则。这一理论的核心观点认为“一切知识都是从感官的感知开始的，在可能的范围内，一切事物都应尽量放在感官跟前，如果得不到实物，就用图像、模型等直观教具代替”[2]。基本于人类的认知特点，人们往往对直观的视觉刺激比对枯燥的文字描述和公式推导更加印象深刻。作者在进行创新性教学活动中体会到，学生在学习新知识时，对那些有实际应用背景以及几何直观性强的内容更容易接受和掌握。因此，针对高等数学下册部分几何直观性强的特点，本文对其教学方法做了新的探索。

同济版《高等数学》下册在第九章第六节介绍了空间曲线的切线方程的求法[1]：设Γ是三维空间中的一条曲线，设其方程为

设M(x0,y0,z0)是Γ上的一个点，下面求在M处Γ的切线方程。假设F,G具有连续偏导数且满足

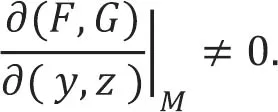
由此（隐函数存在性定理可））在M(x0,y0,z0)的一个邻域内可确定一组函数y=(x)和z=ψ(x)。由此可得曲线Γ的参数方程为：

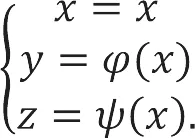
再由曲线参数方程求处切向量的方法，可知Γ在M处的切向量为

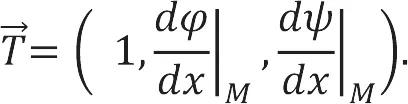
另一方面，根据隐函数求导公式，我们有

其中

进一步化简，可得Γ在点M处的切向量为

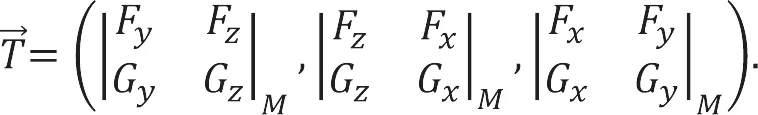
再由直线的对称式方程可知，曲线Γ在点M处的切线方程为

教材在介绍完空间曲线切线的求法之后，紧接着又讲了空间曲面的切平面求法。观察上述推导切线方程的步骤，我们发现其关键点是利用了隐函数存在性定理及其求导公式。这部分知识是前一节的内容，学生刚学完还比较熟悉，因此，这样讲解可以使学生强化之前所学的知识，并且使学生体会到所学知识在解决具体几何问题中的应用，能激发学生的学习成就感。但另一方面，该方法也存在不足，其最大的不足是隐函数求导公式本身就比较繁琐、复杂且推导过程没有几何直观，不利于学生理解与记忆。对公式记忆不牢或记错公式是导致学生考试成绩不理想的一个主要原因，因在在进行高等数学教学时，要尽量地精简公式，减轻学生的记忆负担。本文的一个目的就是通过借鉴文献[3,4]中的想法，探索空间曲线切线新的求法。

不同于同济版教材先介绍曲线的切线再介绍曲面的切平面的次序，我们可以先研究曲面的切平面方程，然后再利用曲线和曲面以及切平面和切线的几何关系，导出空间曲线的切线方程，这样的推导更具几何直观性。具体地，设F(x,y,z)=0表示空间一个曲面，并选取该曲面上的一个点M (x0,y0,z0)，则由同济教材推导[1]可知，曲面在M处的切平面方程为

Fx(x0,y0,z0)(x-x0)+Fy(x0,y0,z0)(y-y0)+Fz(x0,y0,z0)(z-z0)=0.

即Γ看作两个曲面Σ1:F(x,y,z)=0，和Σ2:G(x,y,z)=0的交线。取其上一点M(x0,y0,z0),下面我们求Γ在点M处切线的方程。由于M∈Σ1且M∈Σ2，分别考虑两曲面在该点的切平面：

Π1:Fx(x0,y0,z0)(x-x0)+Fy(x0,y0,z0)(y-y0)+Fz(x0,y0,z0)(zz0)=0.

和

Π2:Gx(x0,y0,z0)(x-x0)+Gy(x0,y0,z0)(y-y0)+Gz(x0,y0,z0)(zz0)=0.

则由几何直观容易看出，Γ在点M处的切线即为Π1和Π2的交线，即所求切线方程为：

因此所求切线的对称式方程为

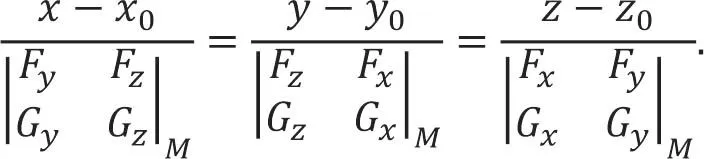
以上是高等教学中一个简单的例子，但却启示我们，讲授高等数学这门课时应该多利用数学对象的几何直观进行新的教学方法的探究，从而使学生更好地学好数学这门课。