基于压强射流板的汽车天窗风振噪声优化

高 骏，杨 易，郑乐典，张 勇，2

（1.湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082；2.湖南工业大学 机械工程学院，湖南 株洲 412007）

0 引言

高速行驶的汽车同时打开天窗或者打开侧窗会导致车窗前沿处发生涡的脱落现象。脱落涡运动至车窗后沿与车体发生碰撞破碎，与车厢内空气相互作用形成的低频高强的噪声称为风振噪声[1]。风振噪声因其自带的脉动压力波动，极易引起驾乘人员的疲劳感和负面情绪，影响乘坐舒适性[2]。

目前，对于汽车风振噪声的控制与优化方法主要是采用改变车窗结构位置和加装气动附件。文献[3]运用仿真分析与风洞试验对低速和高速两种速度工况下的风振噪声进行了相关研究，通过改变汽车窗户开口面积与设计一种网状挡风条结构控制噪声。文献[4]把声压级作为评价以及优化指标，提出了3 种降噪方法：合理开启天窗、设计双空腔结构天窗以及改变天窗前后位置，取得一定的降噪效果。文献[5]提出了前窗导流片、B 柱开槽、后窗加立柱等降噪措施，结果表明后窗加立柱的降噪效果明显优于其他两种。以上降噪方法都会或多或少影响到车辆原本的外观，最终难以被应用于实用车。

本文拟基于对汽车天窗风振噪声的机理分析，提出一种基于压强射流板结构为核心的风振噪声优化方法，以风振噪声的声压级为优化目标，在汽车天窗前沿处添加压强射流板，与汽车原始天窗进行对比分析，验证压强射流结构的有效性。再以射流压强P、射流角度D为优化变量，设计最优的降噪方案。结果表明，压强射流板结构能够有效降低汽车天窗风振噪声，从而提高汽车声学舒适性。所提方法不用改变汽车天窗的原始外形，易于实现且应用前景较好。

1 汽车风振噪声机理

1.1 声反馈机理

高速状态下的汽车车窗开启时可等同于开口空厢，其声反馈机理如图1所示。

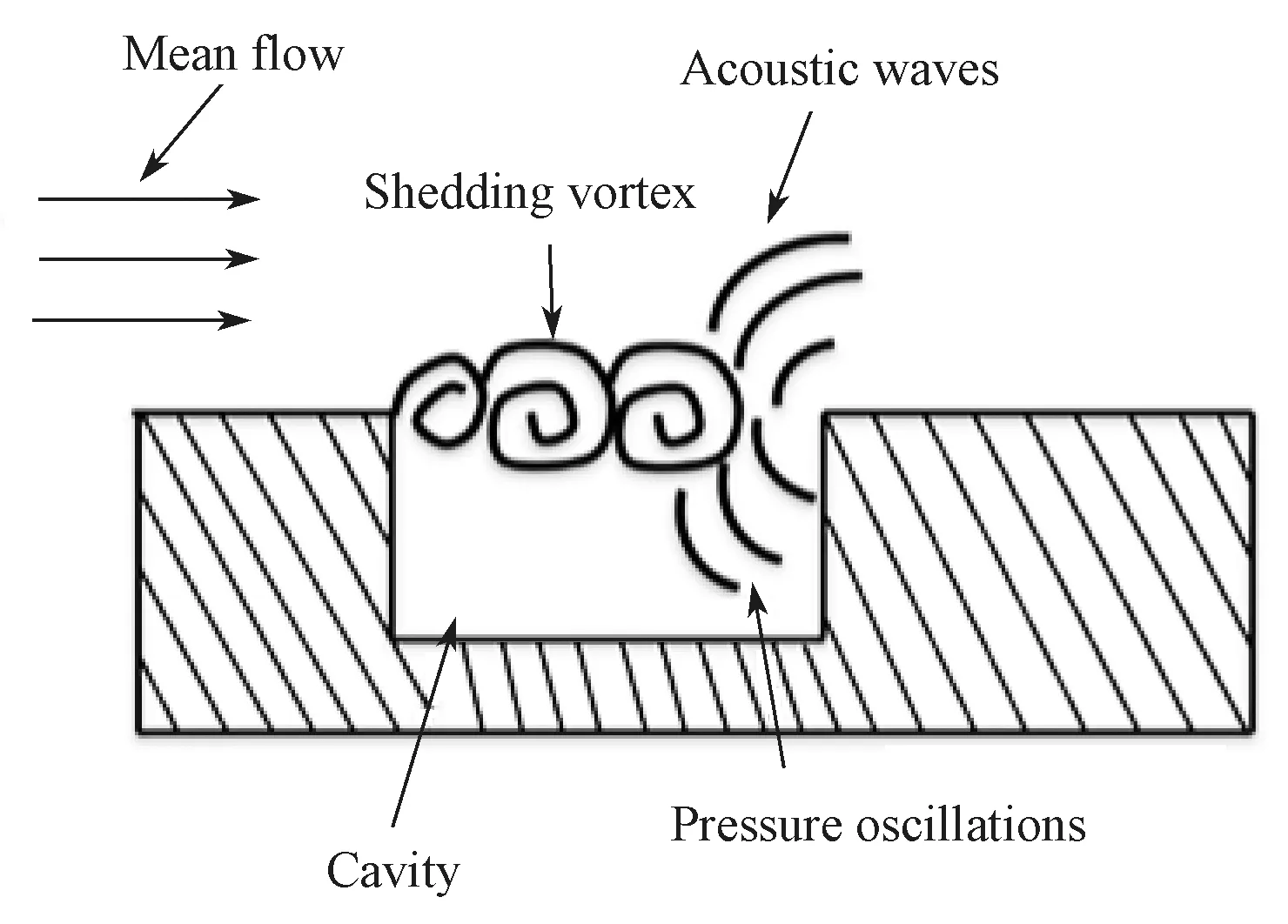
图1 风振噪声声反馈机理示意图Fig.1 Schematic diagram of wind buffeting noise acoustic feedback mechanism

早期的声反馈机理来源于航天航空领域基于喷气噪声试验的半经验公式，最早的半经验公式由A.Powell 等[6]提出。

汽车空腔上游边界产生的脱落涡运动到空腔下游边界时，将因发生碰撞而破裂，脱落涡破裂时产生的声波，一方面反馈到车窗前沿，从而促进剪切层分离涡再次脱落；另一方面，声波向车内辐射，引起车内空气激振，从而产生空腔风振噪声。假定空腔开口的宽度为L，则脱落涡由上游边界到达下游边界所需要的时间为t1=L/uc，其中uc为上游脱落涡的迁移速度，且uc一般为自由来流速度u的0.4～0.6 倍。上游产生的脱落涡碰撞到下游边界时产生的声波反馈到上游边界所需要的时间为t2=L/c，其中c为声速。设脱落涡的周期为T，则T=t1+t2，如果脱落涡的频率为f，则有

式中：n=1,2,3,…，为风振噪声的模态。

把上式改写为斯特哈尔数（Strouhal number）的函数，可得：

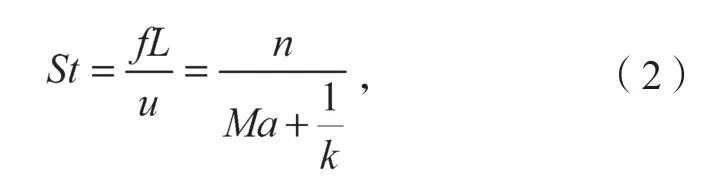
式中：St为斯特哈尔数；

u为来流速度；

k为迁移速度与来流速度的比值，且k=uc/u；

Ma为马赫数。

斯特哈尔数用于反映流体流动的非定常性及振荡模态。由于下游的涡撞击与声反馈之间存在相位滞后，因此 J.E.Rossiter[7]根据实验结果，通过引入常数γ，对公式（2）进行了校准，得到了著名的Rossiter 公式：

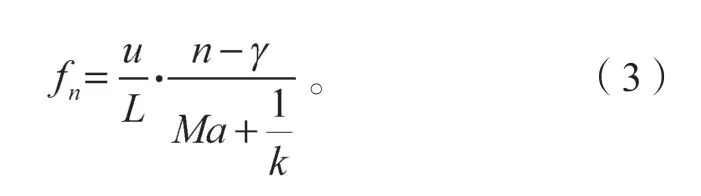
对于参数γ，常被取作经验常数，通常根据实验进行调整。对于浅腔（L/D=4），J.E.Rossiter 给出了一个平均值，即γ=0.25，k=0.57。这一均值已经被证明符合大多数的实验数据，并且γ随着L/D比值的增加而减少。在低马赫数下，文献[8]认为在剪切层和开口后沿的相互作用下，γ可以忽略不计，因此，给定取γ=0，k=0.4。

此过程以某个主频率周而复始地完成，当脉动压力波主频率接近车厢固有频率时，这种共振便会产生，进而引起风振噪声。

1.2 声共振机理

汽车打开天窗或者侧窗时的乘员舱可以被视为空腔，则风振噪声产生的原因，可以解释为脱落涡碰撞碎裂后向车内辐射压力波导致的声共振，其机理与赫姆霍兹共振相似。此时的共振频率及强弱程度与多个因素相关，包括车窗的开度范围、车厢内空间的大小等。

共振厢体的固有频率可以通过式（4）进行估计得出[9]：

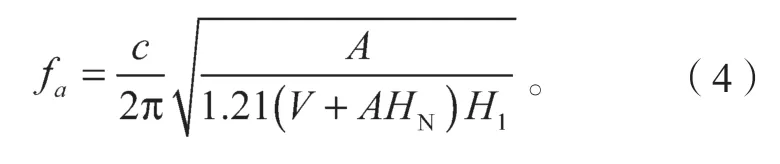
式中：A为车厢开口面积；

V为车厢体积；

HN为声腔开口厚度；

H1为声腔深度，其计算可参考文献[10]。

涡脱落频率f的经验公式如下[11]：

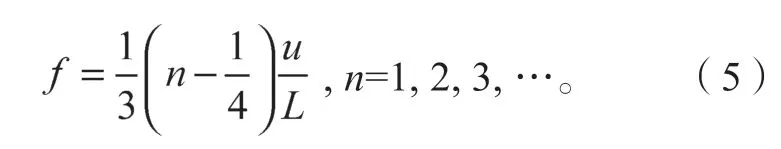
当空腔的固有频率和前沿产生的脱落涡频率相等时，就会产生风振噪声。风振噪声的形成通常是以某一种原因为主体的，但同时又存在着多种因素的相互作用。风振强度主要取决于多因素的共振效应、脱落涡大小、共振频率等，通常不同大小的脱落涡蕴含着不同的能量[12]。

2 压强射流扰流板结构设计

2.1 风振噪声控制方法

根据风振噪声的生成机理，从以下4 个角度进行风振噪声优化。

1）改变脱落涡的尺寸大小。不同尺寸的涡流所包含的能量不同，因此改变涡的大小可以降低脱落涡碰撞后的声压辐射，从而可以降低车内的脉动压力，进而降低声压级。

2）改变涡脱落的碰撞强度。脱落涡从车窗前沿运动到车窗后沿并与后沿发生碰撞，控制脱落涡向后沿运动的速度，可以降低脱落涡与车窗后沿的碰撞强度，从而减弱碰撞产生的风振噪声。

3）改变涡脱落的频率。风振噪声是由于空腔固有频率和脱落涡的频率相等或相近时发生共振产生的，由于空腔固有频率是固定不变的，那么就可以改变脱落涡的频率，破坏空腔共振的机会，从而抑制风振噪声。

4）降低脱落涡与车窗后沿的碰撞概率。通过改变天窗前沿处涡流的运动路径，降低脱落涡与车窗后沿发生碰撞的概率，从而达到降低汽车风振噪声声压级强度的目标。

根据上述方法，在天窗开口前沿引入压强射流结构，射流宽度与天窗前沿同宽，通过破坏及改变车窗前沿处产生的脱落涡频率和运动轨迹，减少脱落涡撞击在车窗开口后沿的概率和强度，从而降低风振噪声的声压级强度。

2.2 结构设计

图2 展示了汽车天窗处的流线情况，流体会在汽车天窗前沿处脱落，并与天窗后沿发生碰撞。碰撞产生的压力波传入车内引发风振噪声。因此，通过在天窗前沿设置压强射流结构，改变天窗处流场便可以控制风振噪声。

图2 汽车天窗压强射流流场示意图Fig.2 Pressure jet flow field of the automobile sunroof

图3所示为汽车天窗整体结构示意图，图4所示为汽车天窗压强射流板位置示意图。

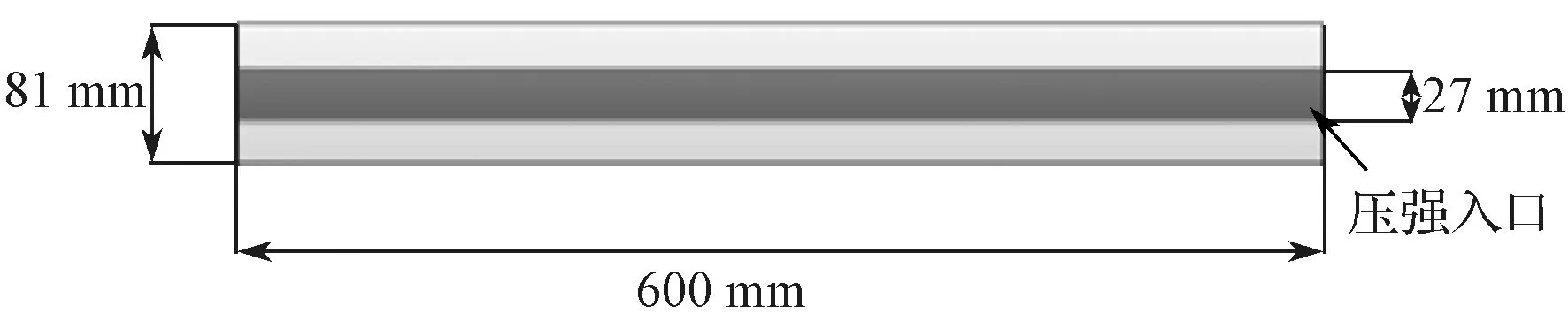
图3 汽车天窗整体结构示意图Fig.3 Overall structural drawing of the automobile sunroof

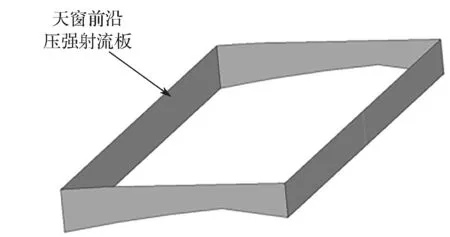
图4 汽车天窗压强射流板位置示意图Fig.4 Schematic diagram of the position of the pressure jet board of the automobile sunroof

如图3所示，其中天窗总开度为450 mm，宽度为600 mm，前沿高度为81 mm。根据天窗处的实际情况，压强射流板结构的形状设计为矩形长条状。图4 正中间的矩形长条即为汽车天窗压强射流位置，其中高度设计为27 mm，为天窗前沿高度的1/3，处于上下居中位置处，宽度和车窗前沿保持一致，为600 mm。

3 数值仿真

3.1 仿真模型与边界条件设置

本研究在数值仿真中选择的是经过适当简化的汽车外形模型，模型的长、宽、高分别为5.0,1.8,1.7 m。计算域的长、宽、高分别为55.0,13.0,8.5 m。简化汽车模型及其仿真计算域如图5所示。

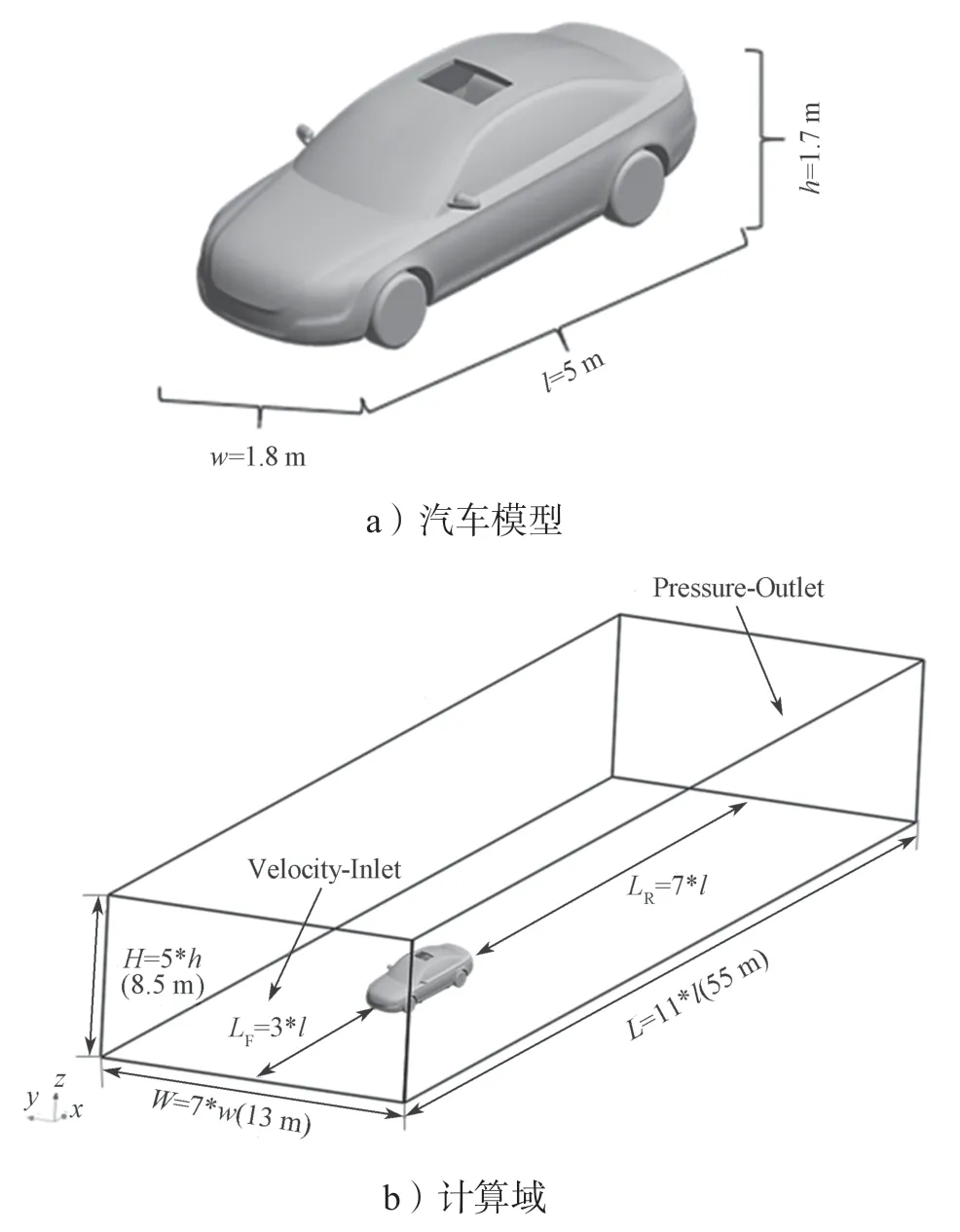
图5 简化汽车模型及其仿真计算域示意图Fig.5 Schematic diagram of simulation calculation domain of a simplified vehicle model

汽车整体的面网格尺寸设置为32 mm，计算域的面网格设置为256 mm。为了保证计算精度的同时能够节约计算资源，计算域中设置3 个密度盒。其中第一个密度盒的体网格尺寸为32 mm。第二个密度盒的体网格尺寸大小设置为64 mm，第三个密度盒的体网格尺寸大小设置为128 mm。考虑边界层的影响，构造了5 层附着在车身表面上的附面层，第一层厚度为1 mm，其后的附面层厚度以1.0:1.2 的比例依次递增。总共用于计算的多面体网格总数约为300 万。

图6所示为仿真模型的y=0 纵截面上的网格划分纵截面图。

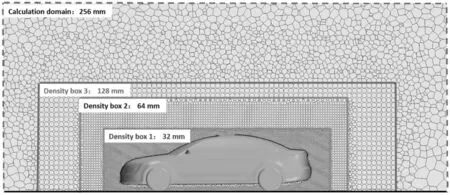
图6 体网格划分纵截面图Fig.6 Volume mesh distribution on the longitudinal section

简化汽车模型的仿真边界条件设置及其求解设置分别如表1 和表2所示，其中把矩形长条区域设置为压强入口，初步设置压强射流的大小为60 Pa，与水平面间的角度D为0 °。

表1 简化汽车模型仿真边界条件设置Table 1 Boundary condition setting of a simplified vehicle model simulation

表2 简化汽车模型仿真求解设置Table 2 Simplified vehicle model simulation solution setup

在流场仿真软件中，先采用Realizablek-ε模型求出稳态流场，待其收敛后，以此为初始值进行瞬态求解，瞬态计算时采用大涡模拟（large eddy simulation，LES），选用Smagorinsky-Lilly 亚格子模型[13]。这样处理可以降低计算资源的消耗，缩短仿真所需要的时间，从而提高仿真效率。在驾驶员右耳处设置监测点，获取此处的脉动压力数据。仿真步数共2 000 步，时间步长设置为0.000 5 s，瞬态仿真时间为1 s，可以获得最大分辨率为1 000 Hz 的噪声信号。除去前面不稳定的0.5 s，最终分析结果取0.5～1.0 s 内的脉动压力结果进行傅立叶变换，获得汽车风振噪声的声压频谱曲线。

3.2 降噪效果验证

降噪效果验证实验中，分别计算汽车原始天窗全部开启和添加压强射流装置后的天窗全部开启时的两种工况，分别测量驾驶员右耳处的脉动压力。图7所示为仿真所得原始天窗和添加压强射流装置后的天窗的脉动压力对比曲线。

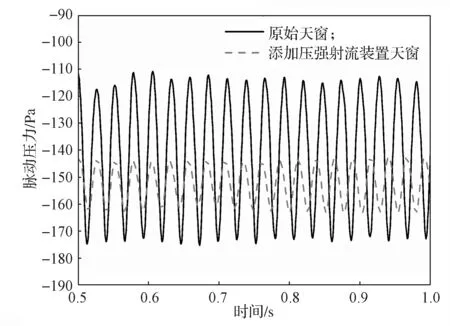
图7 验证压强射流车型与原车的脉动压力对比Fig.7 Comparison of verification pressure jet model and the original vehicle pulsating pressure

从图7 可以看出原车风振噪声脉动压力波动区域是-180～-110 Pa。添加压强为40 Pa 的压强射流装置优化后，车内风振噪声脉动压力区域是-165～-140 Pa，波动幅度从70 Pa 降到25 Pa，降低了45 Pa。

运用傅立叶变换可以得到频域下的声压级曲线，由于风振噪声是以低频为主，所以取频域内的0～250 Hz，原始天窗与添加压强射流装置后的天窗的声压频谱曲线如图8所示。

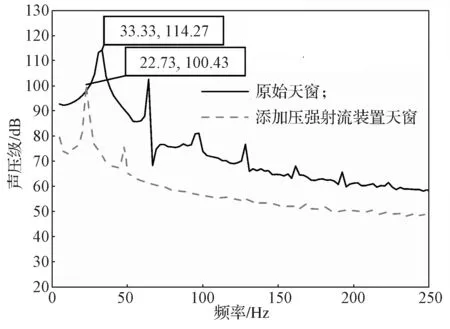
图8 验证压强射流车型与原车声压频谱曲线对比Fig.8 Comparison of the sound pressure spectrum curves between the verification pressure jet model and the original vehicle

由图8 可知，原车的声压级为114.27 dB，峰值频率为33.33 Hz；添加压强射流装置优化的声压级为100.43 dB，峰值频率为22.73 Hz。声压级降低幅度达到13.9 dB，峰值频率减小了10.6 Hz，降噪效果十分显著。

表3 展示了原车和优化后车窗的仿真对比结果。

表3 验证压强射流与原车声压级对比Table 3 Comparison of sound pressure level between verification pressure jet and the original vehicle

图7、图8 和表3 表明，添加压强射流板扰流装置可以有效地降低汽车风振噪声的声压强度。这证明了本文设计的压强射板流扰流结构在降低汽车天窗风振噪声上的可行性。

图9 为汽车原始天窗和添加压强射流装置后纵截面的压力云图对比。

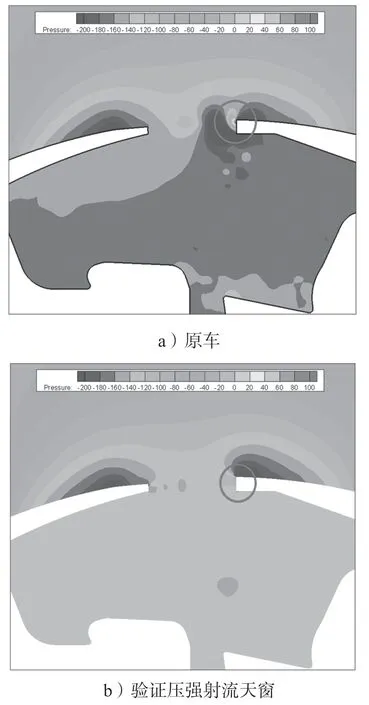
图9 验证压强射流车型与原车压力云图对比Fig.9 Comparison of pressure nephogram between verification pressure jet model and the original vehicle

图10 为汽车原始天窗和添加压强射流装置后纵截面的流线图对比。

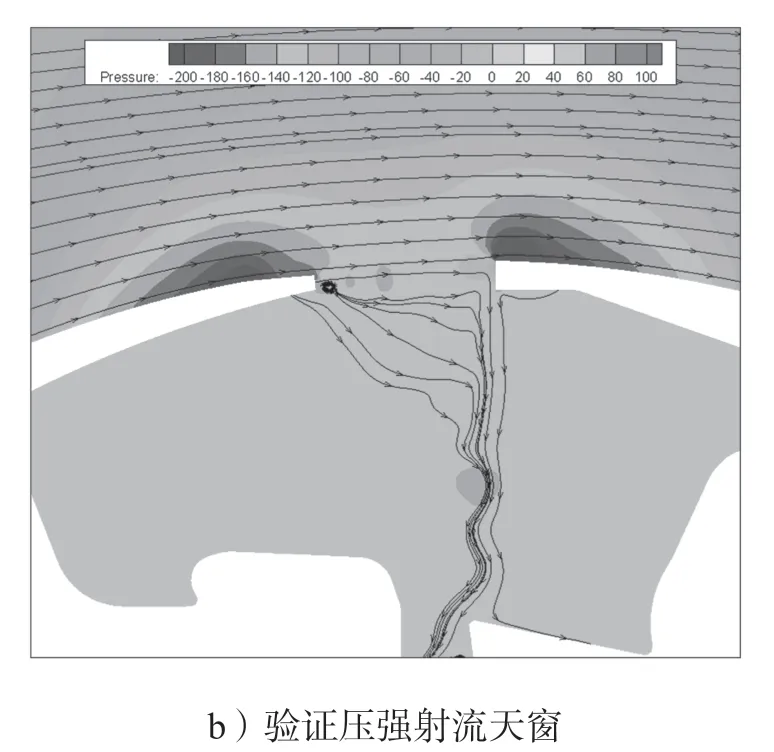
图10 验证压强射流车型与原车流线图对比Fig.10 Comparison of verification pressure jet model and the original vehicle streamline diagram

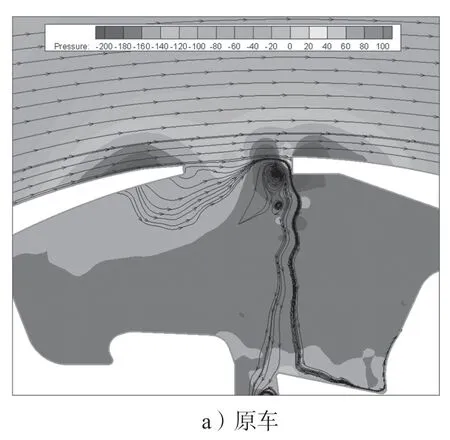
由图9 和图10 可以得知，优化前后脱落涡的尺寸大小和位置均发生了改变：尺寸明显减小，位置向前移动。这可能是因为压强射流装置改变了流场状态，改变了脱落涡的运动轨迹，使得碰到天窗后沿引发破碎涡往车内辐射的概率减少，空腔内负压区明显减少。由图9 和图10所示压力云图、流线图对比的结果，进一步解释了脉动压力图和声压频谱图的结果，更进一步说明在汽车天窗前沿处加装压强射流装置可以有效抑制汽车天窗风振噪声现象，改善进汽车驾驶室内的声学舒适性。

4 天窗压强射流结构优化

4.1 优化变量的选取

压强射流结构安装在天窗上时，压强射流结构的变量参数有天窗压强射流结构与水平方向的夹角度数D、压强射流结构的给定压强的大小P，如图11所示。

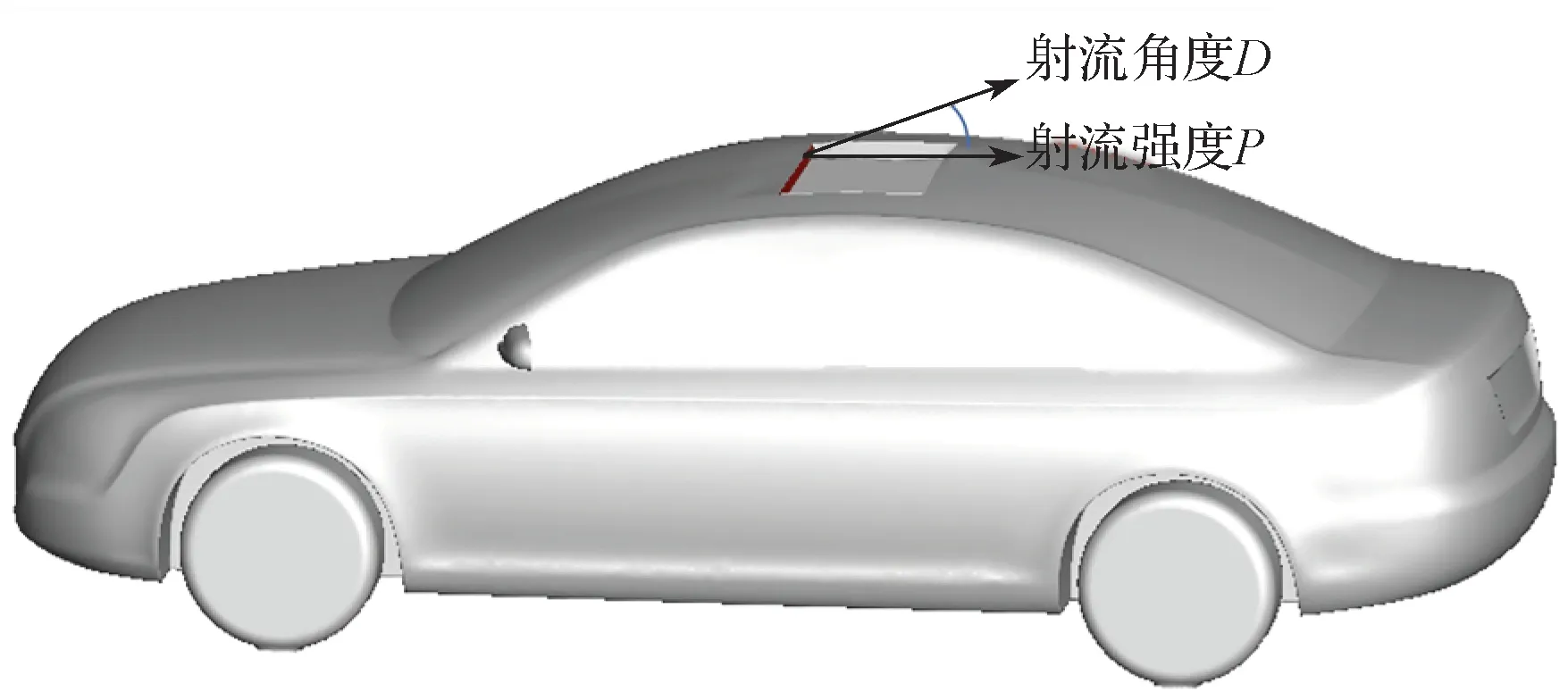
图11 汽车天窗压强射流扰流板示意图Fig.11 Schematic diagram of pressure jet plate for the car sunroof

天窗压强射流结构优化时，取以下参数作为设计变量：

1）P，为压强射流的压强变量。汽车基本行驶速度，由于压强过大会导致压强射流直接撞击车窗后沿反而增大噪声，压强过小又达不到优化效果。压强为负值反而会增加汽车风振噪声的强度。因此，压强的变量只能取正值，经过初步仿真分析确定射流压强P的取值范围为0～100 Pa。

2）D，为压强射流的角度变量（射流方向与水平方向夹角）。角度为负时无法破坏脱落涡，角度值过大会导致汽车气动阻力增大。因此D的取值范围为0°～ 25°。

汽车行驶工况为天窗开度450 mm，车速设置为25 m/s，以驾驶员右耳处监测点的风振噪声声压级作为优化目标。

4.2 优化方案的确定

对于优化变量P，分别取P1=0 Pa，P2=20 Pa，P3=40 Pa，P4=60 Pa，P5=80 Pa，P6=100 Pa。同样也对优化变量D进行等分处理，分别取D1=0°，D2=5°，D3=10°，D4=15°，D5=20°，D6=25°。每一个压强值P和每一个角度值D组合，则总共有36 种方案。

为了确定最佳的优化方案，对每一种方案进行列举分析，从而找出最佳的组合优化方案。列举出所有方案及数值求解的声压级，如表4所示。

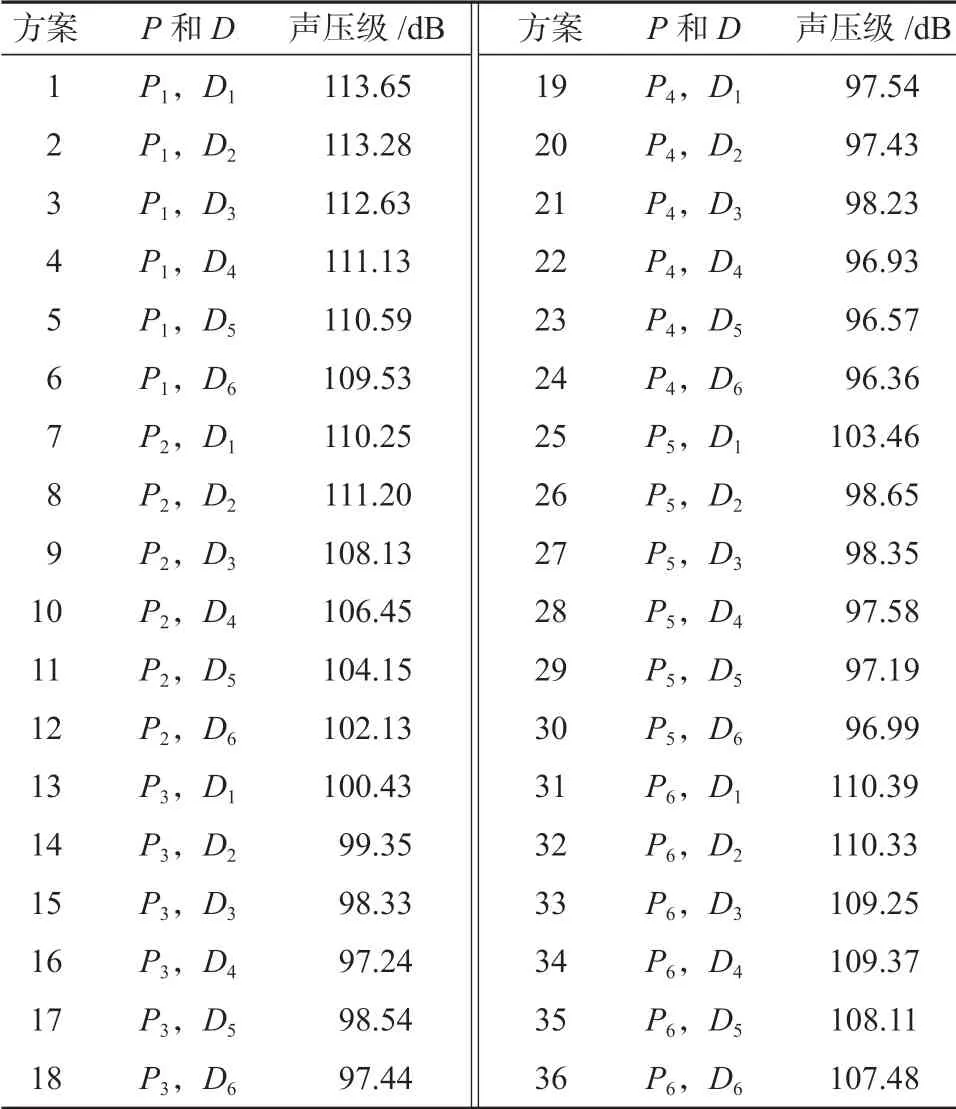
表4 天窗压强射流结构优化方案及其数值求解的声压级结果Table 4 Optimization scheme of the structure of pressure jet of the automobile sunroof

分析表4 中的数据可以发现，随着角度D的增加风振噪声声压级呈现减小的趋势；随着射流压强P的增加，声压级呈现出先减小然后增加的趋势。下面方案均可以降低汽车天窗风振噪声，对比筛选出最优的降噪方案是方案24，P4=60 Pa，D6=25°，对应的声压级为96.36 dB。

4.3 最佳优化方案的降噪效果

对比最优组合方案和原始汽车天窗模型，图12为汽车原始天窗与添加最优压强射流装置后天窗分别开启时的脉动压力图。

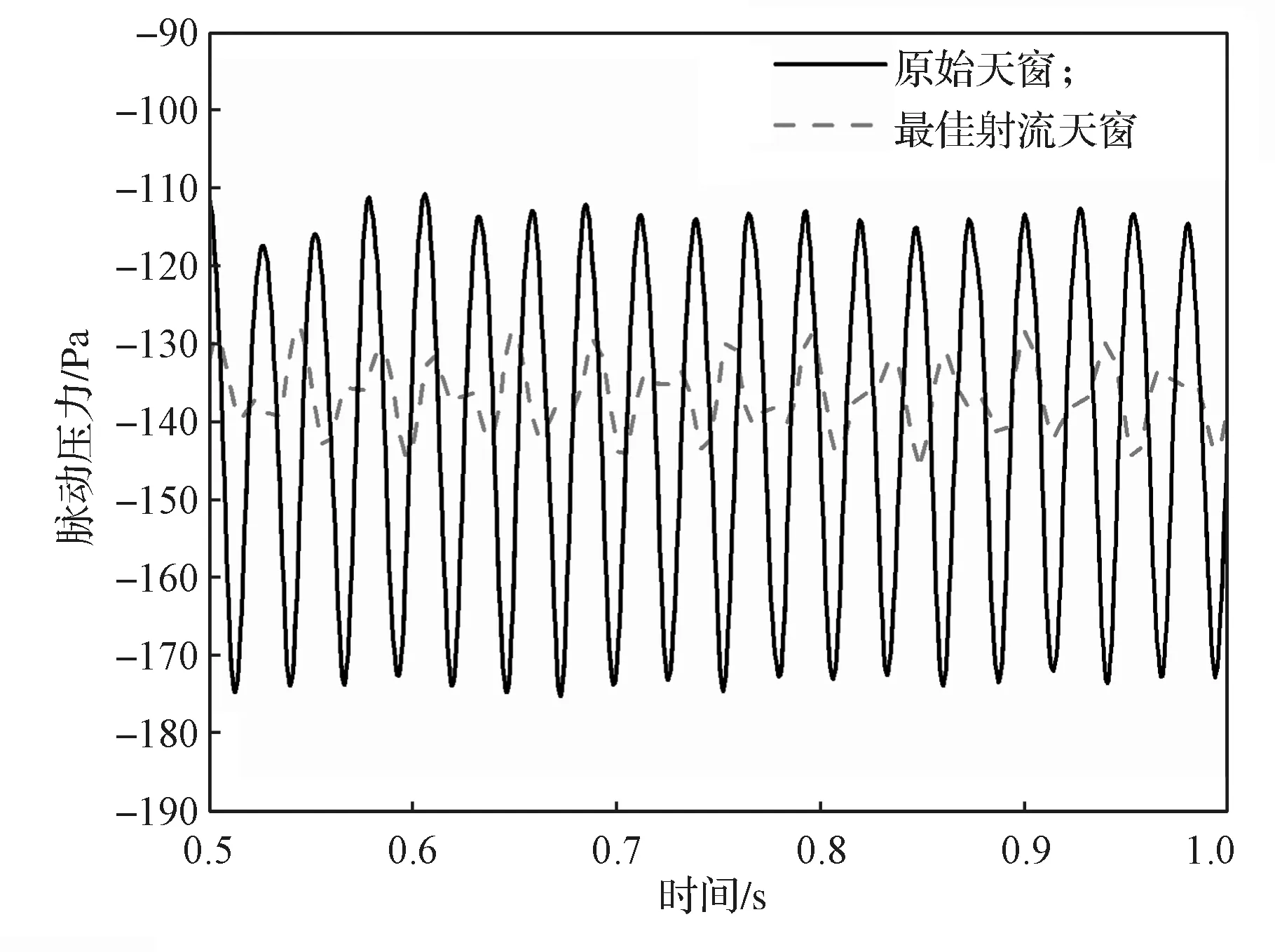
图12 最佳压强射流车型与原车脉动压力对比Fig.12 Comparison of optimal pressure jet model and the original vehicle pulsating pressure

由图12 可知，原车的脉动压力幅值在-180 ～-110 Pa，经过优化的最优射流空气扰流板天窗的脉动压力幅值为-145～-125 Pa，波动幅度约从70 Pa 降到20 Pa，约降低了50 Pa。

运用傅立叶变换，可以得到不同频域下的声压级曲线，如图13所示，最佳压强射流与原车声压级对比结果见表5。

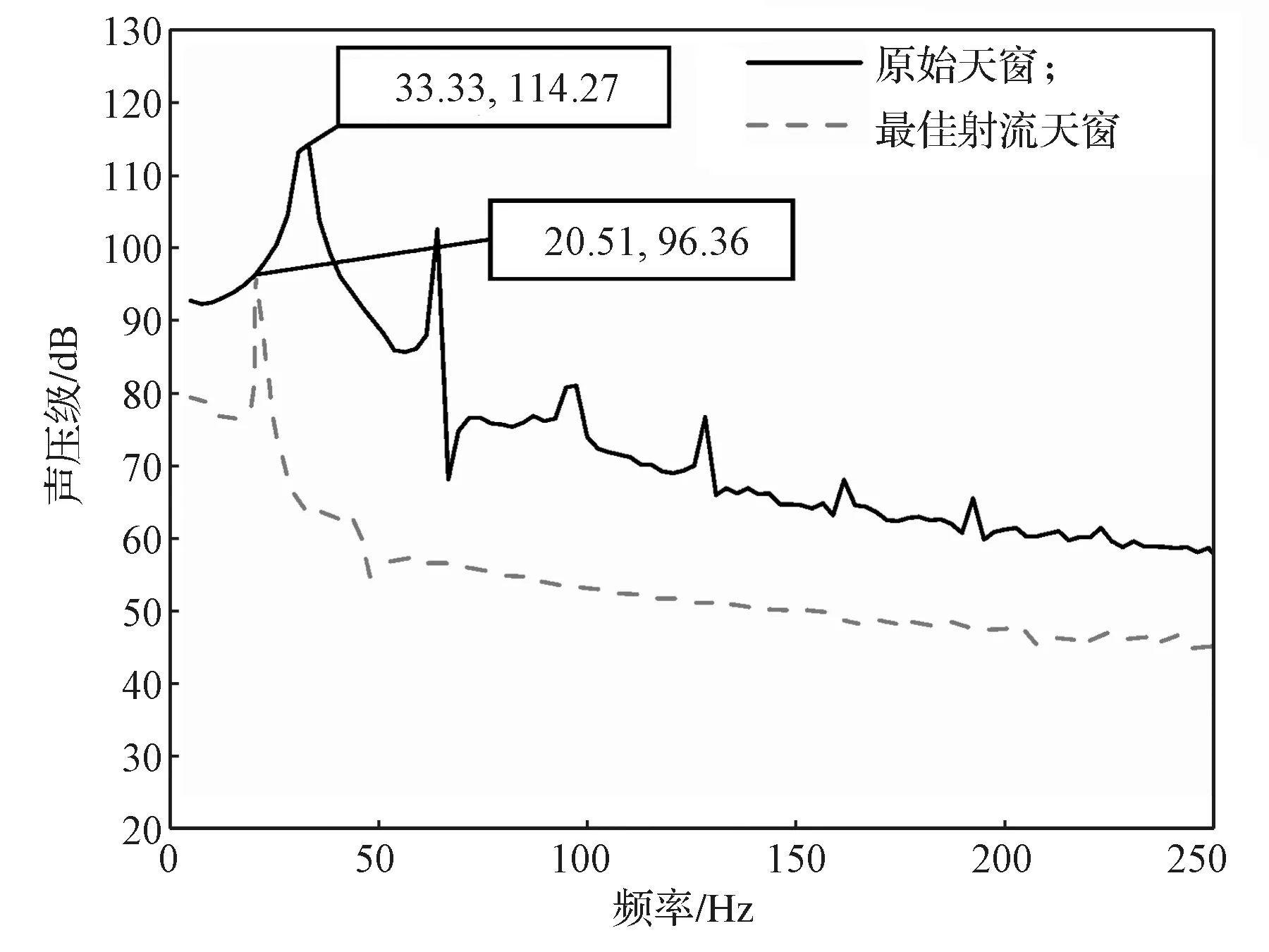
图13 最佳压强射流车型与原车声压频谱曲线对比Fig.13 Comparison of the optimal pressure jet model and the original vehicle sound pressure spectrum curves

表5 最佳压强射流与原车声压级对比Table 5 Comparison of sound pressure level between optimal pressure jet and the original vehicle

由表5 和图13 可以得知，优化后的汽车天窗风振噪声从114.27 dB 降到96.36 dB。与原车相比，脉动压力波动幅度大大降低，最佳压强射流扰流板的优化效果达15.67%。图12、13 和表5所示结果均说明压强射流扰流板结构可以有效降低脉动压力的波动幅度，可以明显降低汽车天窗风振噪声，对提升车内声学舒适性具有重大作用。

5 结语

从汽车风振噪声机理出发，设计了一种压强射流扰流板结构，以实现对汽车天窗风振噪声的控制与优化，该装置可减小脱落涡的尺寸，降低脱落涡与天窗后沿的碰撞强度，改变脱落涡的迁移轨迹，降低脱落涡与天窗后沿发生碰撞的概率，从而降低汽车风振噪声。先选取一组优化方案，验证了此压强射流扰流板结构可以有效地降低汽车天窗风振噪声。再选取多种组合方案，对这些方案进行数值求解，寻找出最佳的优化方案。最后对比最佳压强射流板结构与原始天窗，优化效果可达15.67%，效果十分显著。

此结构可以不改变汽车原有外形，仅通过增加压强射流装置或者从外部导入气流，然后控制压强射流板结构的压强大小和射流角度即可降低汽车天窗风振噪声声压级强度，从而为汽车驾驶舱内提供舒适的声学环境。