基于近似模型的气动升力优化研究

2021-06-30林旗波毛凤朝刘水长曾广胜

湖南工业大学学报 2021年4期

张勇，林旗波，肖业，毛凤朝，刘水长，曾广胜

（1.湖南工业大学机械工程学院，湖南株洲 412007；2.长沙中车智驭新能源科技有限公司，湖南长沙 410000；3.长沙学院，湖南长沙 410082）

1 研究背景

已有研究表明，气动力会随着汽车车速的平方项增大，故当汽车高速行驶时，迅速增加的气动升力会使得部分车型的抓地能力及稳定性能变差[1]，这一现象在赛车领域更为显著。在当前安全、可靠出行的汽车技术背景下，如何提高汽车的高速气动升力稳定性能已不容忽视[2-4]。

由于“地面效应”的存在[5]，导致汽车高速气动升力与其他运载工具有所不同[6]。同时，由于气动升力的敏感性[7]，导致其在数值仿真[8-12]、风洞实验[13-14]、优化理论[15]方面与气动阻力间的差异巨大。如在数值仿真中，S.Y.Cheng 等[16]应用有限体积法（其网格模型如图1所示）和风洞试验法进行了对比研究，得出车辆的气动阻力误差很小，而气动升力误差相对较大的结论。

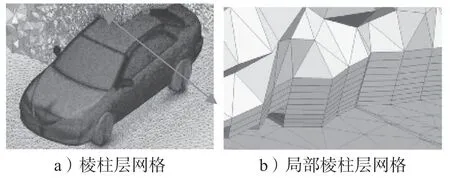
图1 有限体积法网格模型Fig.1 Finite volume mesh model

近年来，随着计算流体力学领域的快速发展，格子波尔兹曼方法（lattice Boltzmann method，LBM）[17-18]获得了广泛应用。LBM 采用介观粒子迁移和碰撞表征流体的宏观流动，避免了有限体积法的网格畸变和汽车车身附面层难以准确表征等计算误差，因而在汽车空气动力学领域得到较好的应用（如图2所示为LBM 法的离散模型与流场）[19]。然而，因为该方法与大涡模拟相结合，求解计算时间的成本较大，所以制约了其在工程中的应用。

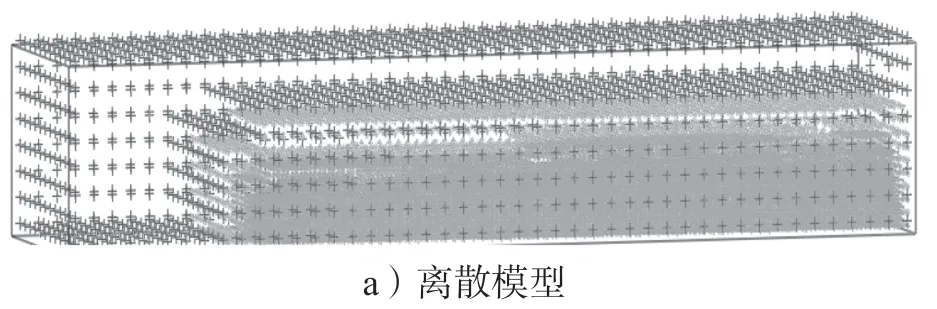
图2 LBM 法离散模型与流场Fig.2 LBM discrete model with its flow field

同时，不同车型的气动升力优化控制，应根据其前、后两轴的升力大小，确定不同的优化目标。如赛车、跑车的优化目标为形成较大的前、后两轴负升力，以增强其抓地能力。而对于轴荷平衡后的乘用车，其情况较为复杂，若其总升力为正，为避免高速时出现发飘现象，应通过车身造型或附加装置来减小车身升力，并适当形成前负后正的前后轴升力分配；若总升力为负，则应避免不必要的轴荷，提高燃油的经济性，形成前轴升力相对趋负，并减小总的负升力的前后轴升力分配。对于自重较大的商用车，为降低其轴荷，应在优化后使得其升力为正。然而，关于这些方面的优化设计及其应用，如今尚鲜有报道。

为给汽车车身设计提供有益的参考，本文拟以某款轿车为研究对象，结合LBM 粒子法、HD-2 风洞实验、优化拉丁超立方设计方法（Optimal Latin hypercube design，Opt LHD）、Kriging 代理模型、遗传算法和车身优化理论，建立一套高效的优化设计方法，并将其应用于某款轿车“前唇”附加装置的优化设计之中，以实现其优良的气动升力特性。

2 汽车模型介绍

风洞实验和数值仿真是汽车空气动力学研究的两种基本手段。受实验条件的限制，并考虑到研究需要，将本研究选用的某款轿车的实验模型分为简化模型与精细模型两种。图3所示为某款轿车按1:3 缩小后的几何模型主体尺寸（单位mm）。图4所示为模拟轿车模型示意图，其中a、b 图为简化模型，c、d 图为原始模型，可见简化模型封闭了进气格栅，删除了底部发动机排气管等细节，该处理是为了便于加工实体模型。

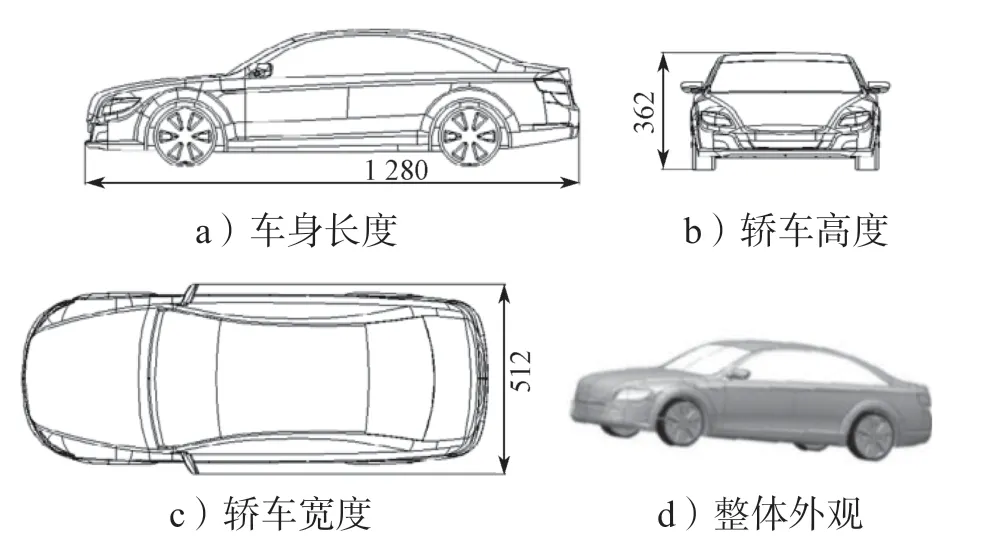
图3 某轿车模型外观及其主要尺寸Fig.3 Appearance and main dimensions of a car model

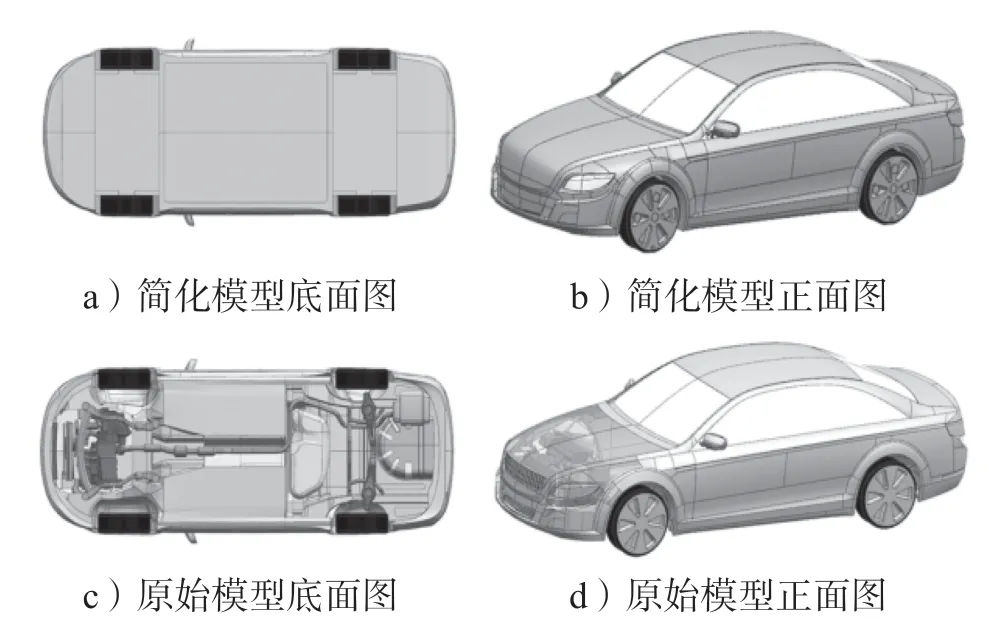
图4 轿车的简化模型和原始模型对比图Fig.4 A Comparison between the simplified model and the original model

3 LBM 数值仿真计算

3.1 LBM 数值仿真方法

LBM 方法将流体视为大量介观迁移与碰撞的粒子微团，系统的宏观参数采用统计方法得到。统计时，设一个计算域内单粒子的分布函数为f(r,ξ,t)，其中，r(x,y,z)为空间位置矢量；ξ(ξx,ξy,ξz)为分子速度矢量，t为时间；f(r,ξ,t)Δξ表示t时刻速度在[ξ,ξ+Δξ]间的分子数，则密度数可表示为

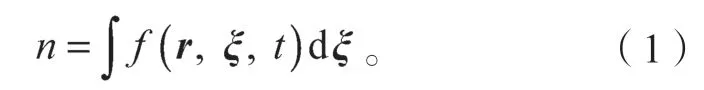
式中n为t时刻r处单位体积内的分子数，即密度数。设任意粒子在时间变量Δt内无碰撞，则分子的位置矢量由r变为r+Δr，而速度将由ξ变为ξ+aΔt，（式中a为加速度）即在时间变量Δt内无碰撞。到t+Δt时，原来t时刻在ΔrΔξ中气体分子f(r,ξ,t)ΔrΔξ将全部不增不减地转移到r+Δr，ξ+aΔt的ΔrΔξ中，则

此时有

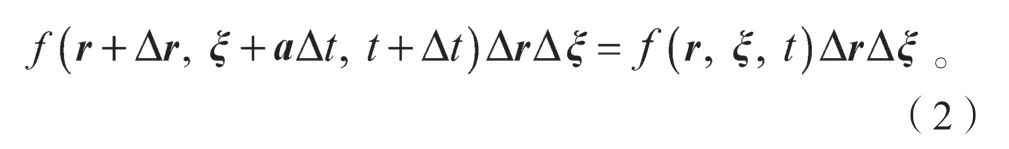
对式（2）左端进行Taylor 展开，两边同除以Δt，并令Δt→0，此时有

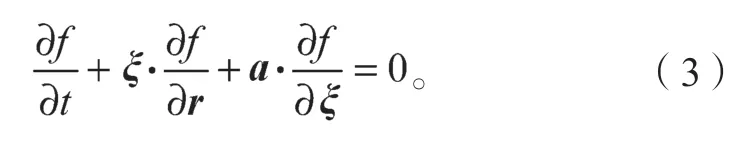
考虑碰撞变化量，则式（3）改为

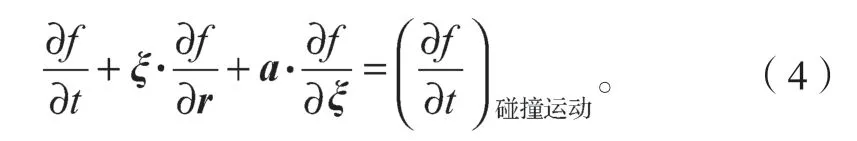
按照1954年 Bhatnagar、Gross 和 Krook 提出的BGK 近似理论[20]，经过系列推导，可将新的粒子分布函数表示为如下Boltzmann- BGK 方程：

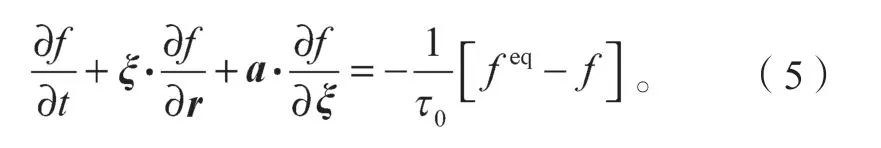
式中：τ0为松弛时间；f为一个计算域内单粒子的分布函数；feq为f的平衡态分布。

将式（5）进行速度离散、时间离散、空间离散处理。空间离散时，按当前最先进的空间离散模型D3Q27 展开[21]，平衡态分布函数写成下式：

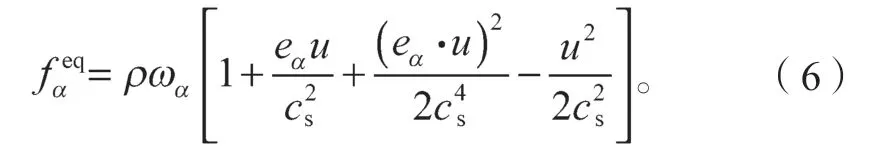
式中：ρ为密度；ωα为权系数；eα为离散速度；u为动力黏度；cs为格子声速。

图5所示为D3Q27 空间离散模型示意图。

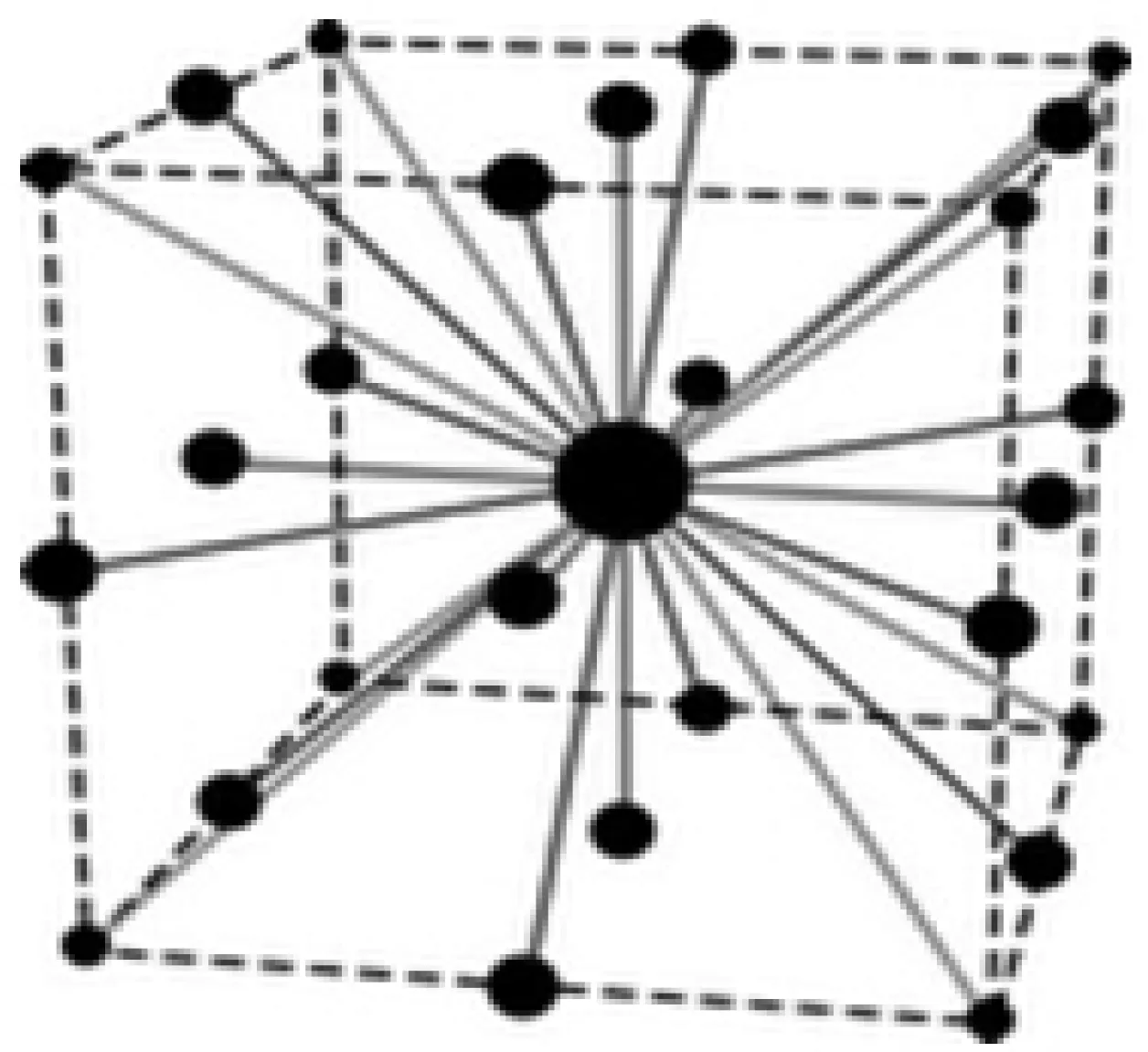
图5 D3Q27 空间离散模型示意图Fig.5 Schematic diagram of the discrete model of D3Q27

由图5 可知，该模型的空间离散是以插值节点粒子形式进行的，因此在形状复杂的三维复杂曲面的汽车空气动力学仿真研究中，具有很好的贴体性，避免了有限体积法中体网格畸变产生的计算误差；同时，自适应的粒子密度分布可以精确地表征车身表面的附面层，因而可以避免人为经验式的附面层划分引起的误差。

格子LBM 的计算过程较为简单，但是对于高雷诺数的求解，其稳定性和精确度存在一定的局限性。若直接开展高雷诺数的模拟计算，不仅需要非常细小的粒子尺度，大规模增加粒子数量，而且对于计算机硬件的要求较高，还会导致计算耗费的时间翻番。为解决这一矛盾，将N-S 方程中描述大尺度涡用的湍流模型，来描述小尺度运动的耗散作用，及其对大尺度运动的反馈作用，即提出了将Boltzmann 方程与大涡模拟相结合的LBM 方法，至于如何将LBM 还原为N-S 方程，详见文献[22]，该方法目前已具有很好的计算精度[23-24]。

对此，本文应用LBM 方法开展汽车气动升力的仿真研究。首先应用图4 中的简化模型开展汽车气动升力研究，并应用HD-2 风洞试验验证该方法仿真结果的准确性。

一般汽车外流场可视为不可压缩定常流场，图4中的简化模型，在车轮静止下，入口速度为30 m/s，常压出口，地面滑移速度为30 m/s，以消除地面效应，其余为静止壁面。采用8 颗Xeon E7-4809-v4CPU，DDR4 内存64 GB，硬盘接口类型为SATA/SAS 的计算平台，耗时113 h，所得LBM法轿车流场如图6所示，仿真实验测得轿车的气动阻力系数Cd为0.264 2，升力系数Cl为0.075 9。

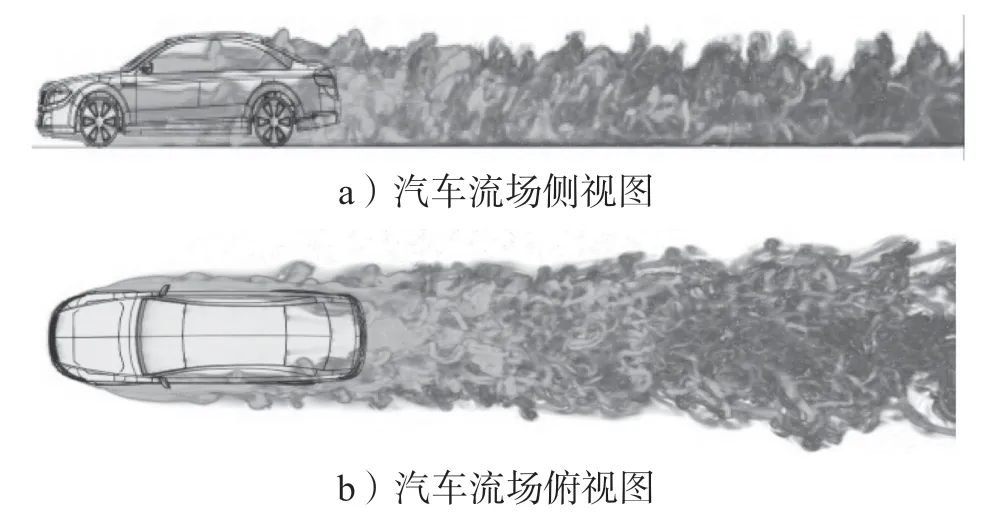
图6 LBM 法流场Fig.6 LBM flow field

3.2 风洞实验验证

将图4所示简化模型进行数控铣削加工，制作成如图7所示的HD-2 风洞实验模型。实验验证时的边界层风洞为如图8所示的HD-2 风洞。

图7 轿车的风洞实验模型Fig.7 Mode for the wind tunnel experiment of the vehicle

图8 HD-2 风洞Fig.8 HD-2 wind tunnel

图8所示HD-2 风洞的高速段长、宽、高分别为17.0,3.0,2.5 m，实验风速为0～58 m/s 连续可调。雷诺数约为1.3×106，阻塞比小于2.7%。测力装置采用六分力浮框式应变式天平，测量精度为0.2%，附面层采用抽吸法移除。

经过7 次实验后，测得图4所示简化车模的平均Cd为0.273 8，Cl为0.073 8。将仿真结果与实验结果进行对比，可知轿车模型的阻力系数误差、升力系数误差分别为3.50%和2.84%，这一结果说明，采用本方法求解汽车气动力具有较高的准确性。

3.3 原始车模气动升力特性

应用验证后的LBM 方法和仿真方案，研究如图4所示的原始轿车模型的气动升力特性。仿真方案与前面的相同，入口速度为30 m/s，同时车轮设置为旋转工况，转动角速度为366.8 rad/s（车轮直径为163.5 mm），结合前后轴分解方法[25]，可得轿车的气动阻力系数Cd为0.279 2，升力系数Cl为0.084 5，其中前轴升力系数Clf为0.039 2，后轴升力系数Clf为0.045 3。

由上述计算结果可知，该车总升力为向上的正升力，其前后两轴亦为向上的正升力，这对汽车高速行驶时的行驶操纵稳定性是不利的，有必要通过改变车身造型或添加附加装置来进一步优化其气动升力特性。由于该车属于两轮轿车，前轮为转向轮，根据前言中提到的优化目标，该车型应减小其气动升力，尤其是通过优化，形成前轴向下的负升力，以增强轿车转向时的抓地能力，进而提高汽车高速行驶时的安全稳定性能。

4 车辆底部改进的气动升力特性分析

在汽车车身设计后期，其造型已定型，不宜进行车身曲面的修改，考虑到工程的经济性与可行性，一般采取增加附加气动装置的方法来实现对气动力的控制，本研究选择将汽车前轴附近的底部区域进行封闭，封闭后的模型如图9所示。

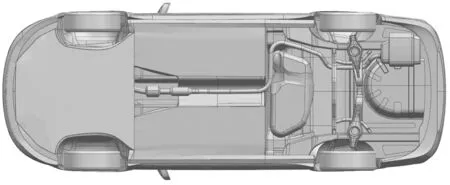
图9 封闭汽车底部后的模型示意图Fig.9 Schematic diagram after the closing of the bottom of the car

应用与上节相同的数值仿真方案，经计算，可得模型的车身上下表面压力云图，并将其与未封闭底部区域的轿车模型计算所得压力云图进行对比，结果如图10所示。

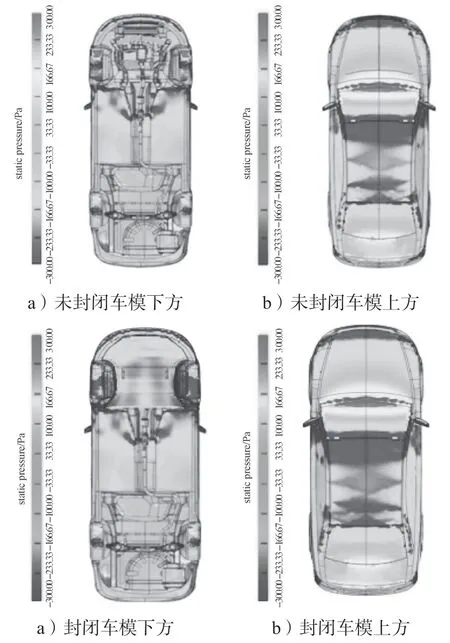
图10 车身上下压力云图对比Fig.10 Comparison of body pressure nephograms

由图10 可看出，将汽车前轴附近的底部区域封闭后，汽车底部前端区域的表面压力趋向负压的面积明显大于未封闭状态的，而上表面的压力未有明显的变化。这是由于车身底部封闭后，前轴附近区域的气流流量减少，导致上下表面压力差增大，最终导致前轴升力趋负。

监测轿车模型的气动力，可以得到封闭后其气动阻力系数Cd为0.267 2，升力系数Cl为0.053 5，其中前轴升力系数Clf为-0.036 9，后轴升力系数Clr为0.090 4。这一结果与压力分布分析结果一致。表明封闭汽车底部后，其气动升力系数降低了约36.7%，气动阻力系数降低了约4.3%，形成了前轴较小的负升力和后轴正升力，这有利于提高前轮转向轮地面附着力，也在一定程度上降低了后轴载荷，改善了车身的气动升力特性。

5 附加装置优化设计

5.1 前齿附加装置设计

由底部改进的气动升力特性检测结果可知，封闭了车身底部，可改善汽车的气动升力特性，使得总的气动升力系数和阻力系数降低，前轴形成很小的负升力系数、后轴形成较小的正升力系数。但这是车身在水平路面行驶时的状态，而在实际车辆高速行驶中，受路面高低起伏等因素的影响，会引起车身俯仰等姿态的变化。诸多研究表明，车身姿态变化引起的气动升力系数和阻力系数均按近似线性急剧增长，其原有稳定的气动升力特性将迅速恶化，表现出地面附着力降低，严重时会出现甩尾和侧倾趋势增强的现象，因而会增加驾驶员的心理恐慌和压力，提高误判、误操作的机率，从而成为高速行驶时产生交通事故的重要诱因。对此，为防止车身姿态发生俯仰时的车头上抬，本研究设计了抑制车头抬起时升力增大的前齿附加装置（简称前齿），如图11所示。

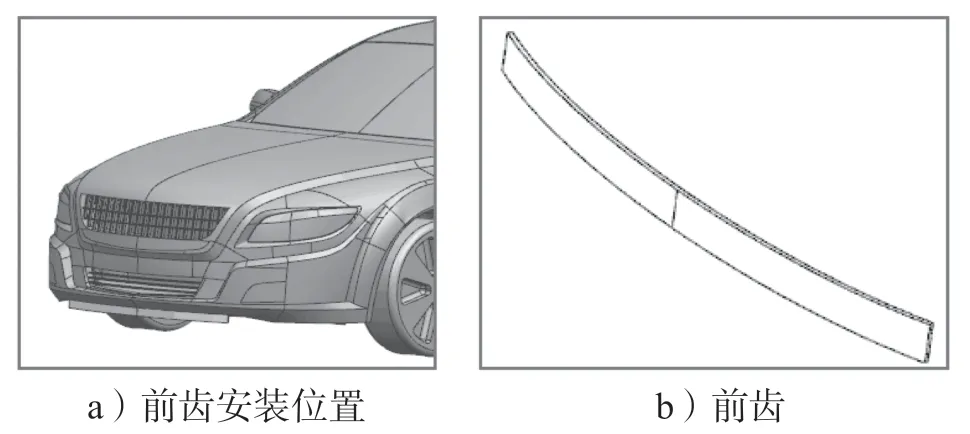
图11 前齿附加装置示意图Fig.11 Schematic diagram with an additional front teeth

如图11所示前齿附加装置结构，前齿紧贴汽车前唇底部边缘安装，并沿纵对称面对称布置。采用橡胶材料制作，在受到硬质障碍时，可挤压变形，因而不会降低车辆的通过性能。而在车辆高速行驶加速状态时，根据前文所述前轴实现负升力的作用机理，前齿可有效减小进入汽车底部的气流流量，以实现更负的前轴气动升力，让前轮贴紧地面，抑制车头的上抬趋势。

5.2 前齿优化数学模型

安装前齿的目的是通过增大车头底部的迎风面积，减小汽车底部的气流流量，最终实现更负的前轴升力。为实现这一目标，需要在车头有限的空间内，通过优化计算得出前齿的最优结构尺寸。

如图12所示，前齿附加装置具有弧长L和宽度H两个特征参数，故需要对这2 个参数进行寻优。

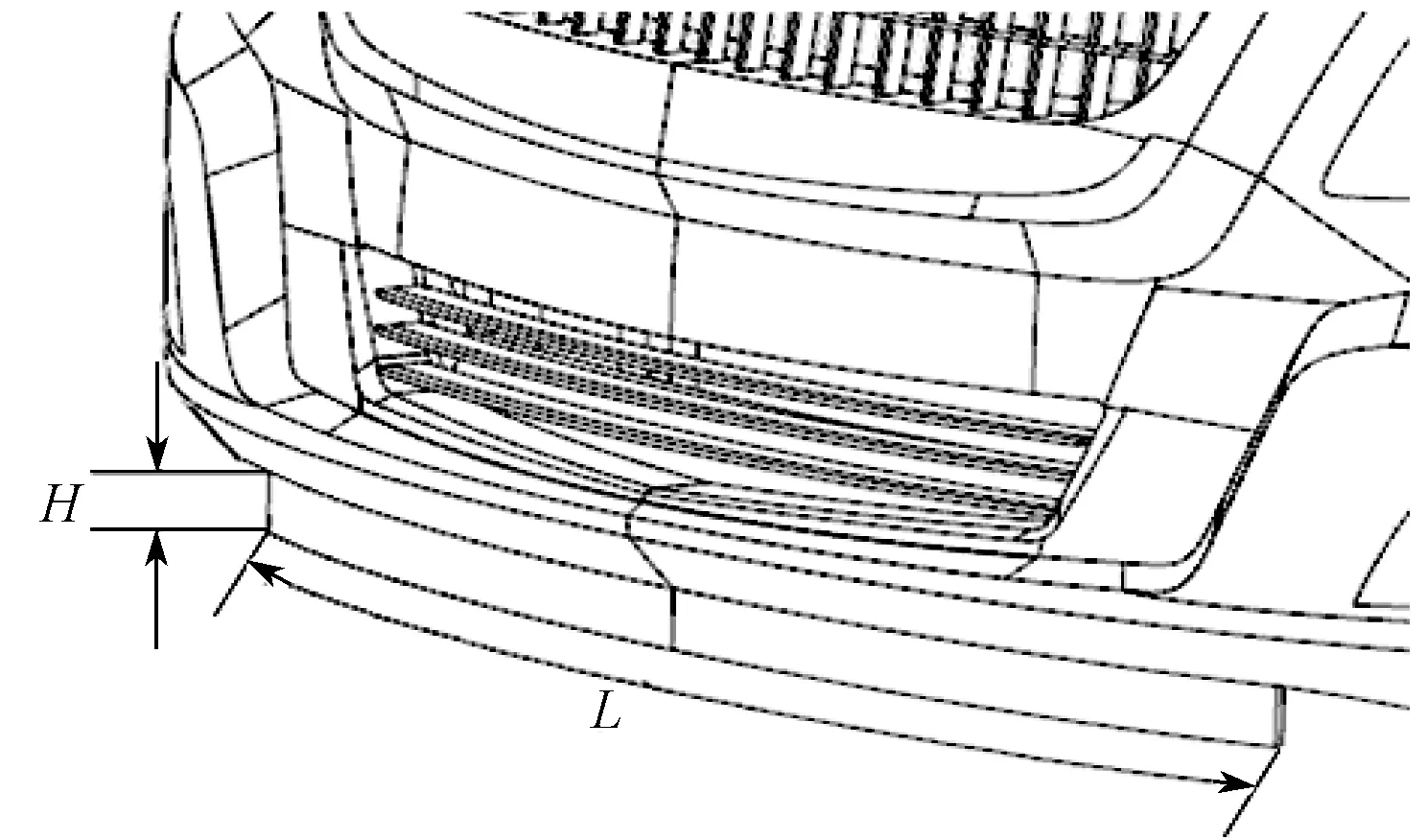
图12 前齿优化参数示意图Fig.12 Schematic diagram of front teeth optimization parametersd

前齿附加装置的结构不同，导致其流场不同，其所能达到的效果也不同。L和H两个参数的取值不同，将引起车身的气动阻力系数、升力系数、前后轴气动升力系数等不同。因此，需要通过控制弧长L和宽度H，使其在有限的空间范围内，获得前轴升力系数Clf最小，即最大负升力，并最终具有工程安装可行性。对此，建立如下工程优化问题的数学模型。

优化目标：Clfmin；

优化变量：L、H；

约束条件：0 mm＜L＜540 mm（区间为汽车前唇边缘轮廓弧长）；

0 mm＜H＜45 mm（最大宽度为汽车模型前唇下到地面间的距离）。

5.3 试验设计与近似模型

由于需要优化的变量较少，为保证设计样本的均匀性，使得响应更为精准，可选取优化拉丁超立方设计方法进行样本点的设计。为保证试验样本点均匀分布在约束变化的空间上，同时为减少计算量，综合考虑计算精确性和计算时间成本，基于优化拉丁超立方设计方法，共设计了9 组样本点，同时建立各样本点的几何数字模型，对图11所示的装有前齿的轿车精细模型，在车轮旋转条件下进行仿真试验，相关计算边界条件及设置的参数与前文相同。应用LBM 进行仿真计算，可获得各样本点的目标函数值，整理如表1所示。

由于LBM 方法的计算精度较高，而计算效率较低，表1 中所述变量不可能穷近或找到最优解，对此，通过构建近似模型的方法逼近最优解。近似模型的构建方法有多种，其中克里格方法（Kriging）是一种空间局部插值的近似模型构建方法，可在有限区域内对变量进行无偏差的最优估计。因本文的研究重点是气动升力，因此只对表1 中的L、H变量引起的前轴气动升力系数Clf的变化来构建Kriging 近似模型，并用相关性系数来评价近似模型的精度。

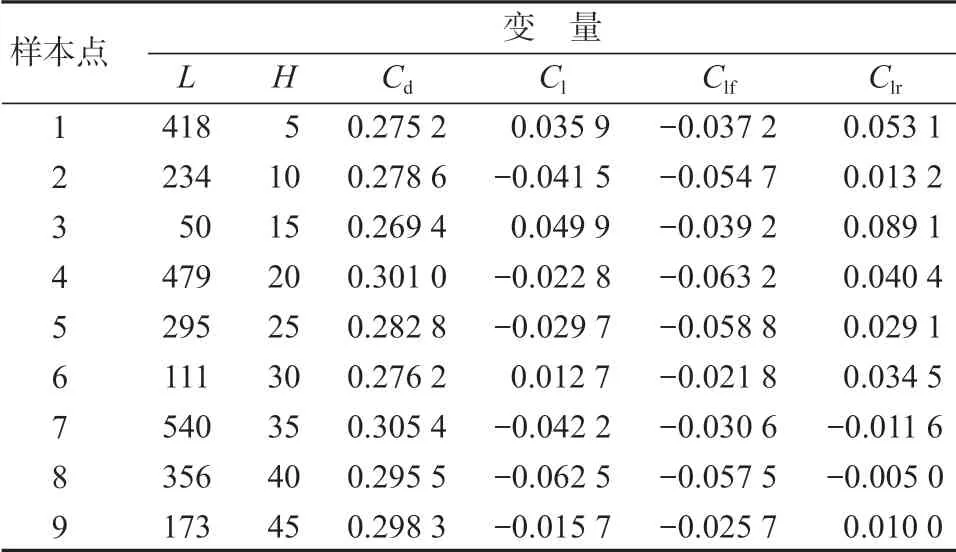
表1 试验设计样本点的目标函数值Table 1 Objective function values of test design samples

图13所示为Clf与L、H的相关性系数图。

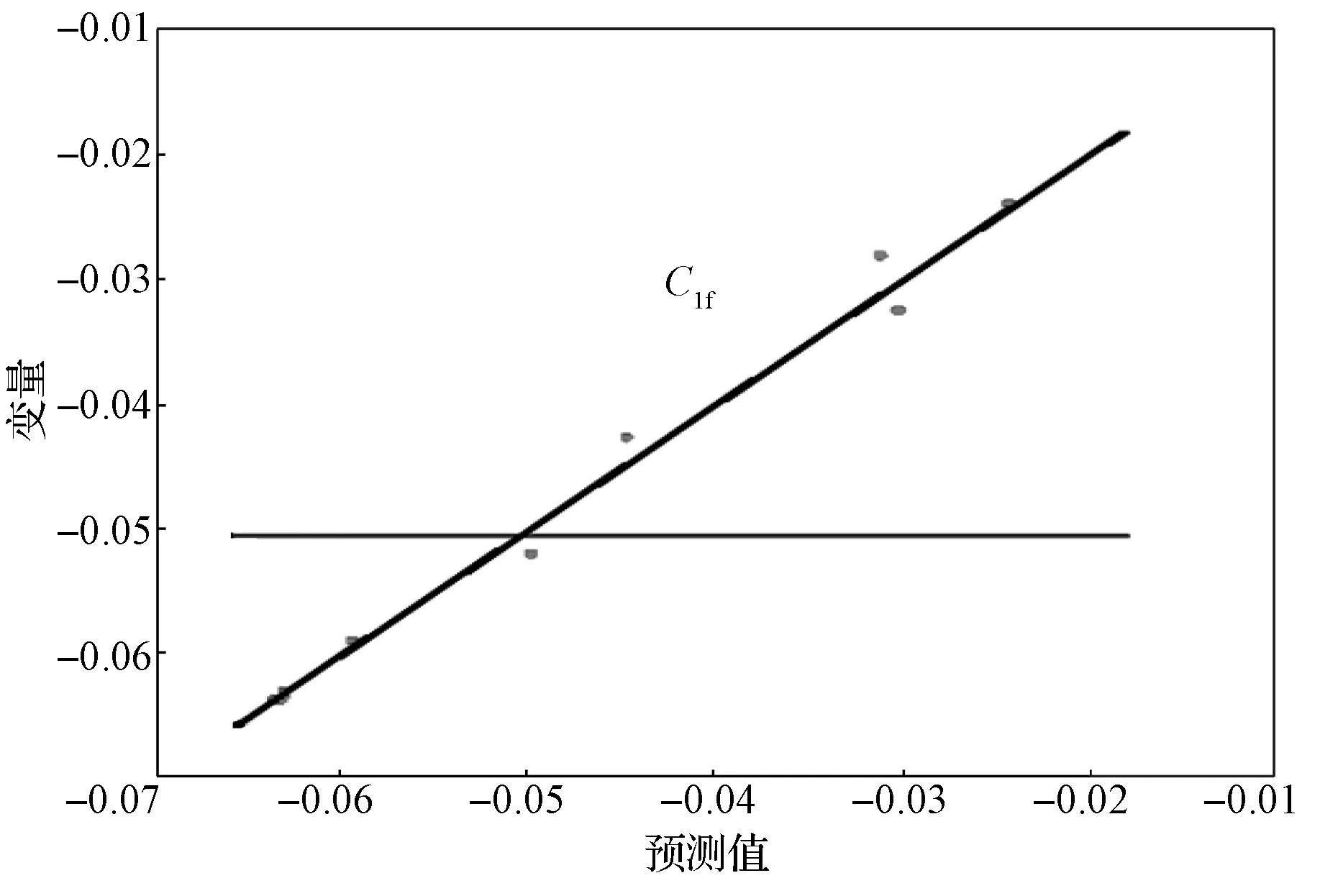
图13 Clf 与变量间的相关性系数曲线Fig.13 Correlation coefficient curve of Clf with the variables

由图13 可知，表1 中的样本均在近似模型曲线附近，经计算，可得误差分析函数的R2为0.975，这一结果表明图13 中的Kriging 近似模型曲线具有较高的可信度。

图14所示为Clf与L、H的主效应图，由图可知，L和H的变换均能引起Clf的变化，且存在极小值，因而可获得最优解。

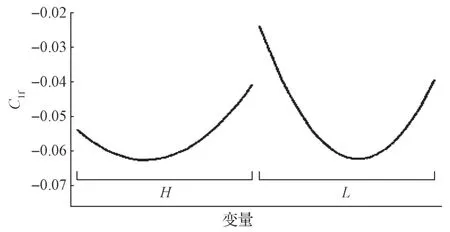
图14 Clf 与变量间的主效应图Fig.14 Main effect diagram for Clf with the variables

5.4 优化算法与结果分析验证

获得最负的前轴升力系数，是一个单目标双变量的寻优问题，根据对图12 和13 的分析，为增加样本的多样性，防止过早收敛，基于Isight 算法，采用多岛遗传算法进行优化计算，计算迭代5 000 步，最终可得最优L值和H值，分别为359.54 mm 和27.46 mm，此时，前轴最负的气动升力系数Clf为-0.063 6。

考虑到优化结果的工程可行性，对L和H在毫米级上取整，则L为360 mm，H为27 mm。按此尺寸，重新对前齿附加装置建立几何数字模型，并应用LBM 法进行仿真计算，以验证优化方法的可行性和结果的可靠性。

计算的边界条件、参数设置仿真方案等与前文所设置的相同。经计算，最终可以得到气动阻力系数Cd为0.305 3，升力系数Cl为-0.082 6，前轴升力系数Clf为-0.063 7，后轴升力系数Clr为-0.018 9，对比该Clf值与表1 中的Clf目标值，可知获得了最负的前轴升力。

图15所示为安装有前齿附加装置的车身上下表面的压力分布云图（前齿为局部放大图中黑色结构）。

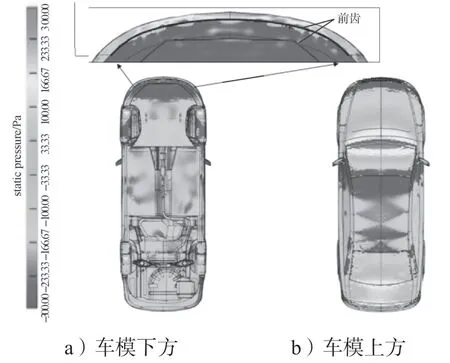
图15 安装前齿的车身表面压力云图Fig.15 Front tooth pressure nephogram

对比图10 和15 可知，安装前齿后的车身底部前端代表负压区域的面积（见图15），相比封闭汽车底部（见图10）处理的负压区域面积更大，且颜色更加深，表明车身上下表面的压差更大，进而导致前轴负升力更加趋向负值。这一结果证明了上述优化方法的可靠性，同时也说明安装前齿附加装置后，对前轴形成前轴负升力的有效性。