机械臂系统任务空间同步的自适应间歇控制

李 欣，马米花

（闽南师范大学数学与统计学院,福建漳州363000）

随着机械臂在日常生活中的广泛应用，它作为一种重要的动力学机械系统，根据需要建立控制程序，渐渐代替人类去完成更多高危险，超负载的任务作业，在工业生产和制造业中扮演着越来越重要的角色[1].在这些实际应用中，如何设计控制器，使机械臂系统能更加安全高效地工作，这一直是一个重要且有趣的研究方向.并且现在已有大量研究成果[2-4].但值得关注的是，在实际的操作中，机械臂末端执行器位置的准确运作需要在任务空间中[5]，我们也将同步控制的思想应用到这一方向上.

本文主要针对存在参数不确定性的网络机械臂系统，在机械臂系统的任务空间中设计一种间歇控制器使得机械臂末端执行器能够跟踪到固定的目标位置.该控制器的设置与现有的大多数机械臂控制成果不同，不用连续接收期望轨道信息而且考虑任务空间来取代关节空间.最后，应用例子仿真结果进一步验证了提出的间歇控制策略可以实现机械臂网络在任务空间对期望轨道的追踪.

1 机械臂系统模型及同步框架

考虑由N个不同智能体组成的网络，其中每个智能体的动力学行为用拉格朗日方程来描述：

性质1(反对称性)矩阵是反对称的，即对任意的

性质2(有界性)存在正常数，成立不等式和

性质3(参数线性化)对于任意的可微向量qi,x,y∈Rn，有其中θi∈R m是拉格朗日系统的物理参数集，Φi∈R n×m为动力学回归方程.

给定一个期望位置xd∈R n是固定点，设计耦合强度c(t)和控制器ui(t)(i= 1,2,…,N- 1,N)使得拉格朗日网络系统的跟踪误差̇ 历时一定时间之后趋于零,从而实现拉格朗日系统在自适应间歇控制下的同步问题.引入参考变量如下：

其中λ＞0.基于式(1) ，考虑如下受控机械臂网络：

其中ui(t)是待设计的自适应间歇控制器，c(t)＞0 表示任务空间上末端执行器位置的网络耦合强度，bij是邻接矩阵表示第i个智能体和第j个智能体之间在任务空间上的位置和速度信息交换，其网络拓扑结构用图GB=(V,ε,B)表示.图的拉普拉斯矩阵记为LB=[lij]∈R N×N.式(4)可写为：

2 自适应间歇控制

设计讨论式(5)的自适应间歇牵制方案.不失一般性，我们选择前l个节点（否则可以重新排列节点顺序）施加控制，从而将自适应间歇控制器ui(t)设计为：

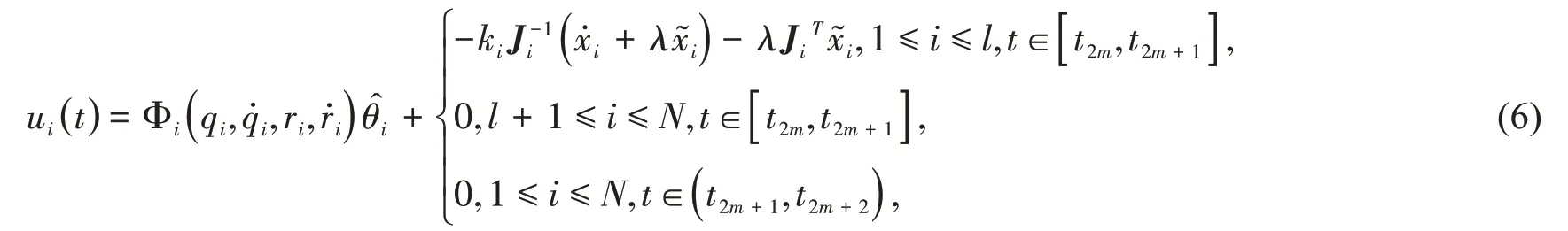
其中η是任意的正数为估计参数误差量.将网络耦合强度c(t)设计为c(t)=c，t2m≤t≤t2m+1；，其中c是待设计的正常数.将式(6)代入统式(5).当t∈[t2m,t2m+1]时，由式(5)得

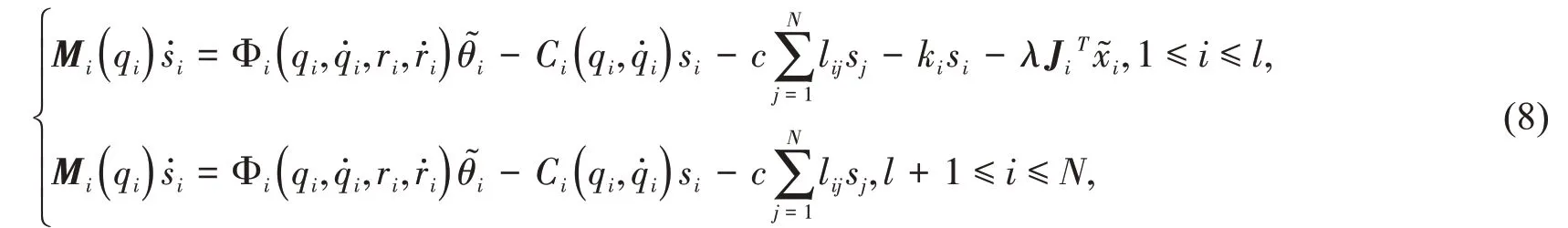
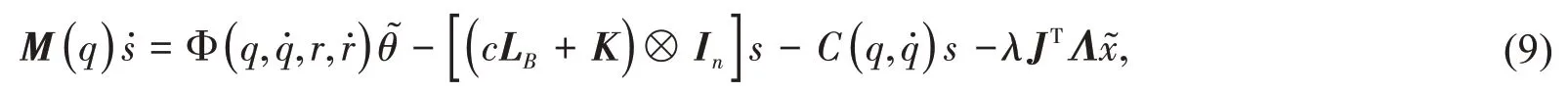
综合上述讨论，可以得到网络机械臂动力系统：

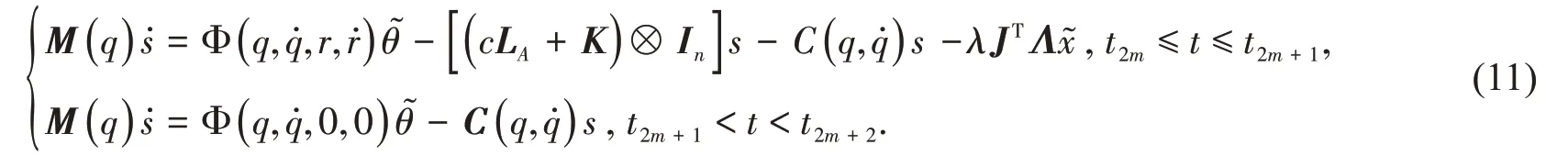
3 任务空间同步分析

在给出重要结论之前引入如下推广的Βarbalat引理.

引理1[2]假设且t0= 0是随κ严格递增的时间序列,函数满足：

定理1考虑有限的任务空间，其中雅可比矩阵为满秩，对于任务空间中给定期望的末端执行器位置xd，选取控制增益ki＞0(1,2,…,l)，λ＞0 和η＞0，那么含参数不确定的网络机械臂动力系统式(11)通过式(6)和式(7)使得系统末端执行器位置追踪到期望的位置，即达到跟踪同步，有当t→∞时

证明引入Lyapunov函数如下

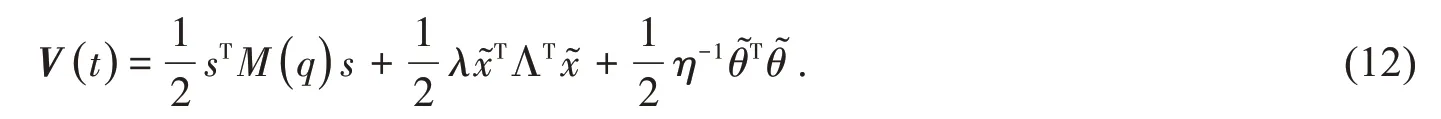
当t∈[t2m,t2m+1]时，V(t)沿着式(11)的第一个方程式求导得

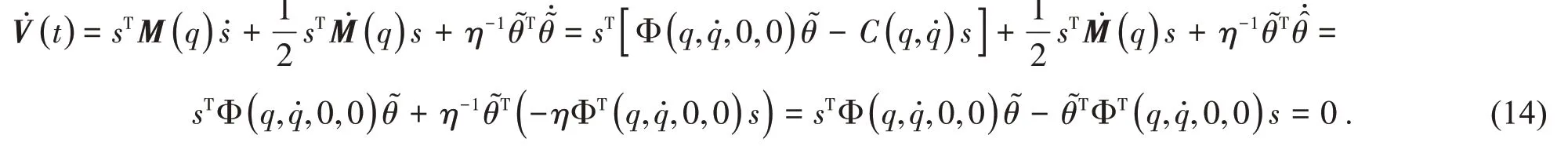
4 理论应用和模拟结果

考虑4 个双连杆机械臂的跟踪同步，其中双连杆机械臂的动力学行为可由拉格朗日系统Mi(qi)q̈i+Ci(qi,q̇i)q̇i+gi(qi)=τi来描述[2-4]，其中i= 1,2,3,4，qi=(qi1,qi2)T∈R2.两个连杆的质量记作mi1和mi2，惯量各记为Ii1、Ii2，长度各记作li1、li2，连接点到杆质心的长度各记作lic1、lic2.

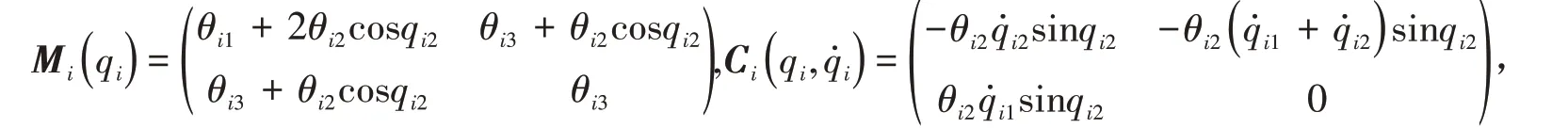
考虑由4 个双连杆机械臂组成网络拓扑结构如图1.这四个节点的度数差分别为2、0、1、-3. 在接下来的仿真中，假设第1 个和第3 个机械臂的物理参数为mi1= 2.0 kg，mi2= 1.8 kg，li1= 1.4 m，li2= 1.3 m，lic1= 0.75 m，lic2= 0.55 m，Ii1= mi1l2ic1/3，Ii2= mi2l2ic2/3，i= 1,3.而第2 个和第4 个机械臂的物理参数取为mi1= 1.8 kg，mi2= 1.98 kg，li1= 1.26 m，li2= 1.43 m，lic1= 0.71 m，lic2= 0.58 m，Ii1= 0.30 m，Ii2=0.22m，i=2,4.取非周期性间歇控制时间如下[0,0.6 ]⋃[1.15,1.8 ]⋃[2.2,2.8 ]⋃[3.35,4 ]⋃[4.4,5 ]⋃….期望的轨道目标取为xd=(2,-3)T.随后，我们考虑控制增益k1=10，k2=10，k3=10，k4=0，λ=10，η=6，耦合强度c= 6，取前3 个节点进行牵制控制.数值模拟结果如图2，机械臂系统末端执行器位置xi( )t可以追踪到目标位置xd.

图1 4个双连杆机械臂的网络拓扑图Fig.1 Network topology of four double link manipulators

图2 跟踪误差‖xi( t )- xd ‖(i = 1,2,3,4)Fig.2 Tracking error‖xi( t )- xd ‖(i = 1,2,3,4)