基于误差传递原理的水尺计重误差分析

朱景林, 朱金善

(大连海事大学 航海学院,辽宁 大连 116026)

1 引 言

水尺计重作为散货船运输中普遍采用的一种货物计重方法,它具有省时省力、低成本、高效率等优点,但在实际操作中存在一定的误差。出入境检验检疫机构规定水尺计重的允许误差为±0.5%[1]。因此,研究水尺计重过程中可能出现的各种误差并采用适当的方法消减误差,对提高水尺计重的精度显得尤为重要。已有的水尺计重误差方面的研究多基于工作实践,系统的理论分析较少,缺乏严谨的逻辑分析与论证。随着船舶大型化的发展,由于港口水深等因素的限制,很多散货船在锚地进行装卸作业,为防止不必要的水尺计重纠纷,保证船舶在锚泊状态下水尺计重结果的准确性显得尤为重要。由于锚链垂直分力对水尺计重精度的影响是一项系统误差,理应通过方法的改进予以消减。

对此,本文在误差传递原理的基础上,明确水尺计重过程中误差的传递过程,并采用适当的方法修正未被有效修正的系统误差,该研究可进一步提高水尺计重精度,确保计重结果更为精确,减少水尺计重过程中的货差,从而避免不必要的货物纠纷。

2 误差的概述

2.1 误差的分类

根据误差的性质差异,误差可分为系统误差、随机误差和粗大误差。系统误差在观测过程中,保持常数或以可预知的方式变化,应通过实验分析的方法,查明其变化规律及产生的原因,并在确定数值后在测量结果中予以修正;随机误差由许多不能掌握、不能控制、不能调节的微小因素构成,可通过多次观测求平均值的方法予以消减;粗大误差是明显超出规定条件下预期的误差,该误差较大,明显歪曲测量结果,要按照一定的判决准则剔除。

2.2 误差传递原理

测量结果的误差是测量方法各环节的所有误差因素共同作用的结果,这些误差因素通过一定的关系作用于测量结果。若对量Y用某种方法测得结果y,则按测量误差的定义,该数据的测量误差为:

δy=y-Y

(1)

设有如下测量方程

y=f(x1,x2,…,xn)

(2)

则间接观测结果的误差可写为:

δy=y-Y=f(x1,x2,…,xn)-f(X1,X2,…Xn)=

f(X1+δx1,X2+δx2,…,Xn+δxn)-

f(X1,X2,…,Xn)

(3)

式中:y为间接观测结果;x1,x2,…,xn分别为各直接观测值;X1,X2,…,Xn分别为相应量的真值;δx1,δx2,…,δxn分别为各观测量的测量误差。

为获得简单的误差关系式,将式(2)按泰勒级数展开,并略去二次以上的高次项,经过简化可得:

(4)

式(4)表明函数的误差是自变量误差的线性和。若把函数看作是间接测量的量,自变量看作是直接的测量结果,则间接量的误差应是直接测量数据误差的线性和。将该误差的这种线性叠加关系推广到一般的情形:

(5)

式中:δy为测量结果的误差;δx1,δx2,…,δxn为各原始误差;a1,a2,…,an始误差相应的系数;aiδxi为局部误差或分量误差。

式(5)表明,测量结果的总误差是测量的各原始数据误差综合作用的结果。这些结果按绝对误差讨论,这是误差传递关系的基本表达形式[2]。

3 水尺计重误差传递机理分析

3.1 水尺计重的步骤

1) 测定有关数据,即观测船舶六面吃水,测定港水密度,测定压载水数量及淡水存量,计算油舱燃油存量。

2) 根据所观测的船舶六面吃水,经吃水标志修正和拱垂变形修正求得最终平均吃水量dM3:

(6)

式中:LBP为船舶两柱间长;lF、lM、lA分别为首吃水点至首垂线的水平距离、中吃水标志至船中的水平距离、尾吃水点至尾垂线的水平距离,三者均可由吃水标志位置图量取;dF、dM、dA分别为船首、船中、船尾平均吃水。

3) 由最终平均吃水查取对应排水量。

4) 经式(7)所示纵倾修正和式(8)所示港水密度修正求得船舶实际排水量,然后分别用装(卸)货后的船舶实际排水量减去全船储备总量以及装(卸)货前的船舶实际排水量得出式(9)所示最终的船舶货物装卸量Ql和Qu[3]。

(7)

Δ=ρΔ1/1.025

(8)

(9)

3.2 水尺计重误差源分析

由3.1节可知,散货船水尺计重工作共需4步进行,而误差来源则集中在第1步和第3步,即测量误差和读图误差。在测量的各环节中,由于条件、设备以及环境等原因的限制,测量过程存在诸多误差。这些误差由不同因素导致,以致误差的性质和特征不同,可分为系统误差、随机误差和粗差。

本文主要讨论水尺计重过程中存在的系统误差,通过合理的方法修正尚未被修正的系统误差。

考虑到水尺计重过程中不同因素的限制,梳理出了存在的系统误差及修正方法如表1所示[4～12]。

表1 水尺计重中的系统误差源及修正方法Tab.1 System error source and correction method in draft survey

由表1可知,如吃水标志不在首尾垂线及船中,船舶中拱或中垂变形,船舶纵倾等系统误差源已被修正。而锚泊装卸时锚链的垂直分力造成的系统误差和靠泊装卸时缆绳的垂直分力造成的系统误差尚未被修正,因此理应通过合适的方法削减该误差,限于文章的篇幅,本文仅研究锚泊装卸时,锚链的垂直分力造成的系统误差的修正。

3.3 误差传递过程

在测得六面吃水后,经计算测得船舶排水量进而得到水尺计重的最终结果属于间接测量范畴。若把函数值看作是间接测量的量,自变量看作是直接的测量结果,则间接量的误差应是直接测量数据误差的线性和。

水尺计重误差传递集中在第2步和第4步,即利用公式计算和修正的过程中,求取最终平均吃水,查取初排水量,纵倾修正计算,港水密度修正计算以及装(卸)货量的计算等。

3.3.1 求取最终平均吃水时的误差传递

由式(6)可知最终平均吃水的函数式可表示为dM3=f(dF,dM,dA),3个变量对于结果的影响是独立的,各原始误差对测量结果的作用也是独立的,因此本次传递过程可以按照绝对误差传递关系进行推算,这是水尺计重误差的第1步传递。

3.3.2 查取初排水量时的误差传递

初排水量是根据dM3从载重表或静水力数值表中直接查出。在查取时,先查得与dM3邻近的整数吃水值对应的排水量作为基数,再将差额吃水乘以相应的TPC得出差额吨数,并与基数相加(或减)得出对应的初排水量。

因为dM3是由式(6)求得,本身含有误差,故与dM3邻近的整数吃水值和与实际值邻近的整数吃水值可能不同,因而对应的排水量基数可能不同。当整数吃水值不同时,相应的TPC也不同,且差额吃水不同,造成差额吨数可能不同;当整数吃水值相同时,即对应的排水量基数相同,但差额吃水不同,必然导致差额吨数的不同,进而影响初排水量的取值,这是水尺计重误差的第2步传递。

3.3.3 纵倾修正时的误差传递

3.3.4 港水密度修正时的误差传递

由式(8)可知港水密度修正公式是关于Δ1的一次函数,港水密度为实测已知量,而Δ1是根据式(7)求得,因此该过程亦存在误差传递,这是水尺计重误差的第4步传递。

3.3.5 计算装(卸)货量的误差传递

船舶装(卸)货前的排水量是未经纵倾修正的排水量,自身可能含有误差,因此在计算过程中会产生传递,影响最终结果,这是水尺计重误差的第5步传递。

4 锚链垂直分力计算

当船舶锚泊在有风、流的锚地时,为防止船舶漂移,锚链与船舶成某一角度连接到海底,此时,船舶会受到一个斜向下的拉力(锚链张力)。根据力的分解原理,该拉力在水平方向上的分力用于抵消风、流的荷载,使船舶在水平方向上的合力为零,此时船舶保持静止(对地)在水面,以便顺利装卸货物。而此时锚链在垂直方向上的分力会使船体下沉,导致观测到的船舶六面吃水增加。本文拟根据JTS144-1-2010《港口工程荷载规范》(《规范》)中风流荷载的计算公式,同时结合前人的研究成果选用较为精确的方法计算散货船的风流荷载,并结合力学原理,推算出散货船锚泊时的锚链垂直分力,该值可作为锚链垂直分力这一系统误差源的修正量。

4.1 船舶所受风压力以及水流力

在综合考虑影响船舶所受风压力和水流力的各种因素的基础上,从《规范》附录E中的公式计算风压力及水流力[13～17]。同时结合力的合成原理,建立船舶风流外力计算模型,如式(11)～式(15)所示,

(11)

(12)

Fxc=(Cxsc+Cxmc)ρV2B

(13)

(14)

(15)

式中:Fxw、Fyw分别为风压力的横向分力和纵向分力;Axw、Ayw分别为船舶横向和纵向受风面积,其大小与船舶总载重吨有关;Vx、Vy分别为横向和纵向风速分量,其大小与风速和风舷角有关;ζ1为风压不均匀折减系数,其大小与船长有关;ζ2为风压高度变化修正系数,其大小与船高和吃水有关;Fxc、Fyc分别为水流力的横向分力和纵向分力;Cxsc、Cxmc分别为水流对船首横向分力系数和船尾横向分力系数,其大小与锚地水深和吃水有关;Cyc为水流力纵向系数,其大小与船长、船宽、船高、流速和水温有关;ρ为海水的密度,一般取1.025 t/m3;V为水流速度;B为船舶吃水线以下的横向正投影面积,其大小与总载重吨有关;S为船舶吃水线以下的表面积,其大小与总载重吨、船长、船宽、船高和吃水有关;T0为风流外力的合力。

在实际应用的过程中,具体船型和船舶的实际装载情况决定了水平面上船体的受风面积,若缺乏相应的船舶资料,根据《规范》附录E,可确定散货船受风面积、风压不均匀折减系数ζ1、风压高度变化修正系数ζ2如表2～表4所示。

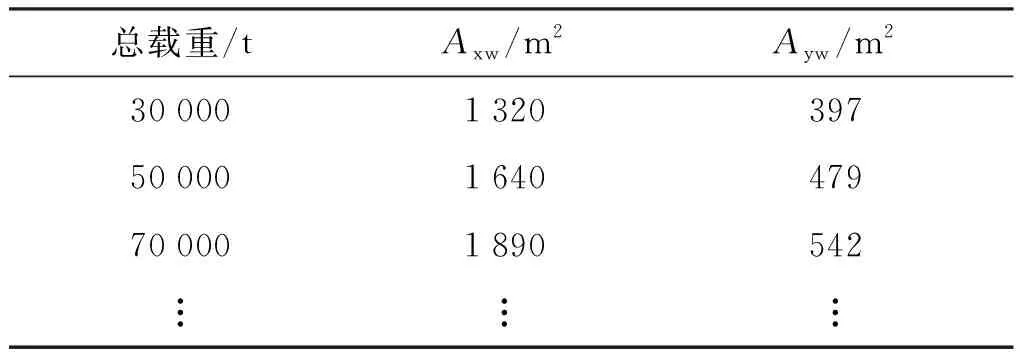
表2 散货船受风面积Tab.2 Wind farm surface area

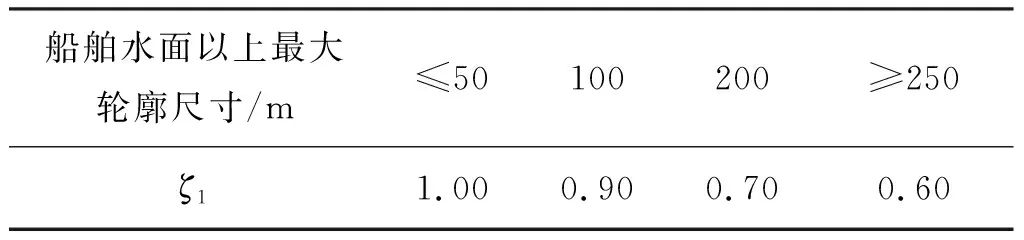
表3 风压不均匀折减系数ζ1Tab.3 Wind pressure unevenness reduction factor ζ1

表4 风压高低变化修正系数ζ2Tab.4 Wind pressure high and low change correction coefficient ζ2

根据《规范》附录F,可确定船舶首尾横向分力的系数如表5所示。

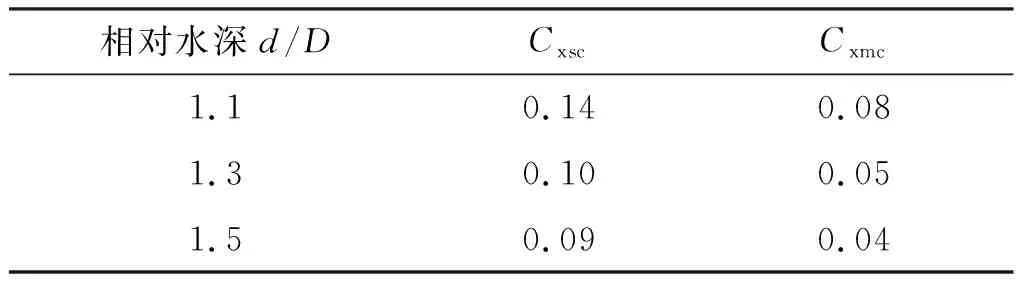
表5 船舶首尾水流力横向分力系数Tab.5 Horizontal flow coefficient of the first and last water flow of the ship

散货船吃水线以下的横向正投影面积B为:

lgB=0.484+0.612 logDw

(16)

式中Dw为船舶的载重量。

水流力纵向分力系数可按式(17)确定,

Cyc=0.046Re-0.134+b

(17)

式中:Re为水流对船舶作用的雷诺数;b为系数,散货船一般取0.006或0.009。

(18)

式中:L为船舶吃水线长度,m;ν为水的运动粘度,m2/s,可根据水温确定,详见表6所示。

表6 水的运动粘度Tab.6 Table of the movement viscosity coefficient of water

4.2 单锚泊船舶出链角度计算模型

单锚泊是指船舶在锚地抛一只锚进行锚泊的方式,与其它锚泊方式相比,具有操作简单,抛、起锚方便等优点,是运输船舶最常采用的锚泊方式[18]。但无论船舶在锚地采取何种方式锚泊,都须保证安全合适的出链长度,以使锚泊船受到足够的约束力来抵抗风、流等外力,从而做到安全锚泊[19]。以单锚泊为例,由于受到重力作用的影响,锚泊船的出链长度分为2个部分,如图1所示。图1中,s为悬链长度(锚链垂悬的部分)；l为锚链平卧在海底的部分,称为卧底链长；h0为锚链孔至海底的垂直距离；α为锚链的出链角度。船舶锚泊时,锚链处于弯曲状态,但随着风流的增大,其将越趋近为直线。故为方便计算,本文近似将悬链长度s按直线考虑。

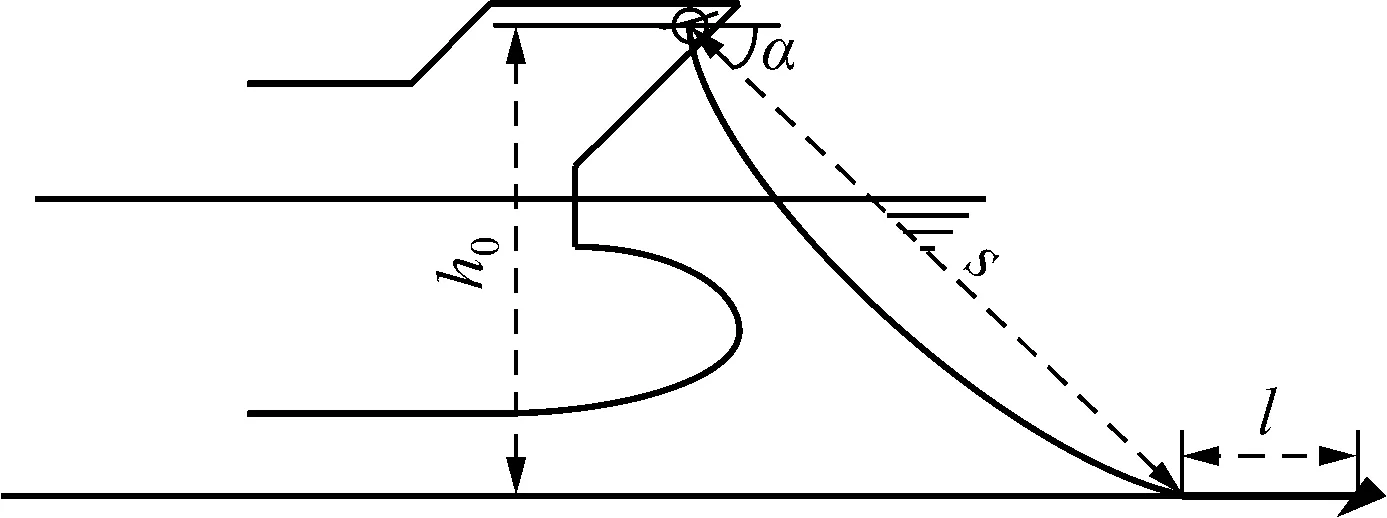
图1 单锚泊船舶示意图Fig.1 Schematic diagram of single anchored ship

根据单锚泊船舶实际锚泊状况、船舶所受风流外力情况以及在该锚泊状况下悬链长度的计算,建立锚链出链角度的计算模型:

(19)

式中:α为锚链的出链角度;h0为锚链孔至海底的垂直距离,其大小与锚链孔至船底的垂直距离、吃水和锚地水深有关;T0为风流外力的合力;Wc为单位链长锚链的重量。

4.3 锚链垂直分力计算模型

在锚泊系统中，由锚抓力和锚链抓力带来的抵抗风流外力的锚泊力是通过悬垂部分的锚链传递到锚链孔处作用在船体上，使船舶在水平方向上合力为零。因此，根据本文4.1和4.2节中有关风流外力和出链角度的计算模型，建立锚链垂直分力的计算模型：

(20)

式中:λc为锚链的抓力系数;l与出链长度有关。

式(20)可作为锚链垂直分力的计算模型,可通过求解船舶所受风流荷载及船舶锚泊状态求出锚链的垂直分力。

从式(9)可知,船舶装(卸)货量是装(卸)货前后2次计重差值得到,这2次计算时锚链和缆绳均在拉直的情况下,其垂直分力引入的系统误差通过式(9)可以消除,但是由于船舶水尺和载重量或静水力曲线表并非是线性关系,该系统误差仍然存在。故在进行水尺计重工作时,应分别在装(卸)货前后计算锚链垂直分力,以得到更为精确的计重结果。

4.4 算例

为了验证锚链的垂直分力对散货船水尺计重的影响,以在舟山港马峙锚地(海图水深15.4 m)锚泊的57000DWT散货船由空载(货物重量为0)装货至满载(理论货物重量为57 000 t)为例,计算装货后由锚链的垂直分力造成的货差及该货差占总体载货量的比重。为方便计算,风流、荷载单位均使用t,g取9.8 m/s2。船舶的主要参数见表7所示。

表7 船舶的主要参数及数据Tab.7 Main parameters and data sheets of the ship

由表2并运用插值法可得：Axw为1 727.5 m2,Ayw为501.05 m2,ζ1为0.73,ζ2为1.48,查阅港口风况资料,取风速为13 m/s,风舷角为45°。根据式(11)和式(12)可得作用于船舶上的风压力的横向分力Fxw为116.03 kN,纵向分力Fyw为22.44 kN。

在该锚地锚泊时,查阅海图可知相对水深约为1.2,分别取水流速度为2,4,6,8 kn(1 kn=1.852 km/h),流向角为10°,水的密度为1.025 t/m3,水温为16℃。由表5可知Cxsc为0.12,Cxmc为0.065,由式(11)可算出散货船吃水线以下的横向正投影面积B为2 480.82 m2,船舶吃水线以下的表面积S为9 452.21 m2。根据式(13)和式(14)可得水流对船首横向分力Fxsc、船尾横向分力Fxmc以及水流对船舶作用产生的水流力纵向分力Fyc。此时,由式(15)可得,锚链的水平约束力Fc,求得数据见表8。

表8 不同流速下的水流力及锚链水平约束力Tab.8 Water flow force and anchor chain horizontal binding force at different flow rates kN

已知锚链孔至海底高度h0为20.6 m,单位链长锚链重3.26 t，根据式(19)可得锚链的悬链长度s以及锚链的出链角度α,根据所求结果选择适当的出链长度。锚链的抓力系数λc取0.75,则根据式(20)可得锚链垂直分力F,求得数据如表9所示。

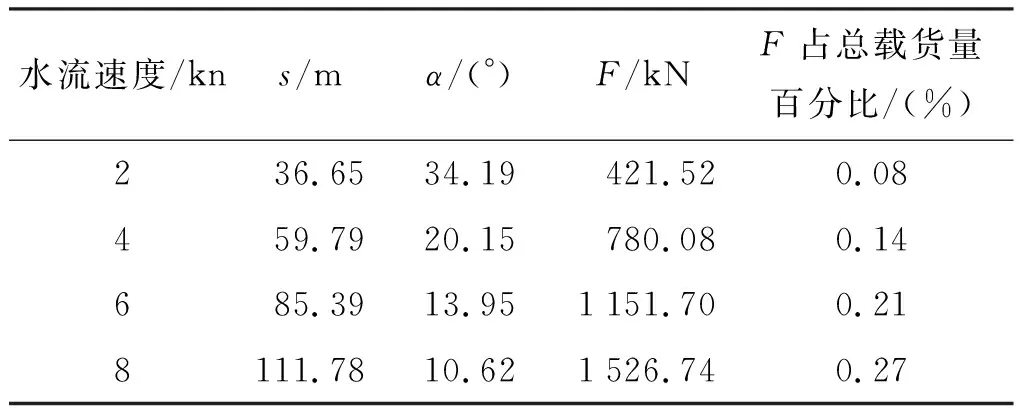
表9 不同流速下的锚链出链角度及垂直分力Tab.9 Angle and vertical component of the chain at different flow rates

结合上述结果经换算可知,在风速为13 m/s,流速分别为2 kn,4 kn,6 kn,8 kn时的锚链垂直分力,在不同流速下该力分别带来了43.00 t、79.60 t、117.52 t和155.79 t的货量误差,分别占总载货量的0.08%、0.14%、0.21%和0.27%。而水尺计重允许的误差范围为0.5%,因此应根据计算结果削减该误差对水尺计重精度的影响。

5 结 论

通过对水尺计重误差的梳理及其传递过程的分析,明确了锚链和缆绳的垂直分力这一系统误差尚未被有效修正。本文在现有的方法中选用较为精确的方法计算散货船的风流荷载;通过对船舶所受风压力和水流力的横向和纵向分力的分析,结合力学原理,以单锚泊船为例建立了单锚泊船所受锚链垂直分力的数学计算模型,可用于计算基于船舶风流荷载的锚链垂直分力;最后,以57000DWT散货船在舟山港锚地锚泊为例,在不同风流外力的作用下,得出了锚链的垂直分力计算结果。结果表明在风速为13 m/s,流速达到4 kn时,仅这一项误差就已达到了水尺计重允许误差的28%,因此理应对该误差进行削减。但该模型也存在一定的局限性:如实测船体受风面积较为困难,而《规范》中给出的受风面积的获取方法却只能计算出满载船舶的受风面积。因此后续研究中应找出更为方便、精确的方法计算船体所受风压力。