考虑区间弹性连接的结构动力学特性研究*
2021-06-26陈亦文张锦光
陈亦文,张锦光
(1.武汉大学后勤保障部,武汉 430070;2.武汉理工大学机电工程学院,武汉 430070)
0 引言
当前,工程实际中的结构系统如火箭、导弹、卫星、高铁、船舶等日趋复杂,复杂结构系统通常由不同形状的板、梁等结构构成主体结构,由大量机械连接(如螺栓、铆钉等)进行装配。然而这些机械连接并非“纯”刚性连接,而是刚度较大的弹性连接,为了提高结构系统的可靠性和环境适应性,连接刚度的影响不容忽视[1-2]。文献[3-4]对具有弹性连接结构的动力学特性进行了研究,文献采用6 自由度标量弹簧对连接刚度进行等效,然而这种方法忽视了连接刚度6 自由度间的耦合作用,等效精度不足。文献[5-6]指出,空间梁单元的刚度矩阵存在6自由度间的刚度耦合,可更为准确地描述机械连接刚度。此外,工程中的机械连接通常有许多参数(如几何尺寸、材料参数等)具有不确定性,这些不确定因素有可能导致结构的固有频率漂移,因此,在研究弹性连接的动力学特性时,应充分考虑不确定因素带来的影响[7-8]。
近年来,区间分析方法在处理区间结构动力学问题方面的应用日益增多,而在处理此类问题的过程中,区间分析方法的核心问题是有限元控制方程的求解[9]。目前用于求解区间方程组的常用方法为区间摄动法[10]以及组合求解法[11],然而,这两种方法均较难实现考察结构某一区间不确定参数对结构动力学特性影响的目的,IFM 的提出则可有效地解决这一问题。文献[12-15]基于IFM 对区间结构的振动特性以及动力响应开展了研究工作,并总结出了IFM 的基本思想和使用步骤,即:1)将结构的区间参数写成其区间中心值与区间因子乘积的形式;2)将区间结构的质量矩阵、阻尼矩阵和刚度矩阵分别写成确定性质量矩阵、阻尼矩阵和刚度矩阵与结构区间参数区间因子乘积的形式;3)将区间结构的固有频率、振型,以及动力响应等写为包含各区间参数区间因子显式的函数,并基于区间分析方法计算所关注对象的区间上下限和区间中心值。
此外,对于日益复杂的工程结构,其离散后的自由度往往是数以十万、百万计,因此,直接利用传统的有限元方法计算其动力学特性,对计算机的工作性能带来了严峻挑战。动态子结构方法是处理分析复杂结构动力学特性的高效方法,常用的动态子结构方法包括时域的CMS 和频域的FBSM。CMS 方法是一种高效计算理论模型耦合动力学问题的时域方法,目前已在商业软件中得到应用[16-17],但由于该方法对于处理试验模型的耦合问题存在限制,因此,FBSM 得到了越来越多的关注。FBSM 的发展经历了从最初的阻抗耦合方法到导纳耦合方法,再到后来可用于直接处理多个子结构间耦合问题的广义导纳耦合方法[18-20],直到形成现有可用于处理考虑弹性连接的多个子结构间耦合问题的FBSM[21-23],其计算精度和计算效率不断提高,适用范围也越来越宽,在工程实际中得到了广泛应用。
基于上述阐述,笔者利用具有区间弹性模量和比例阻尼系数的零质量空间梁单元,模拟复杂结构中的区间弹性连接,综合动态子结构方法和区间因子法,提出了计算考虑区间弹性连接结构动力学特性的高效时域和频域方法,即CMS-IFM 和FBSM-IFM,并通过数值仿真对两种方法进行了验证。相比传统的有限元方法计算动力学特性,该方法不再受计算机工作性能的限制,可大幅提高计算效率,为大规模的推广应用奠定了基础,可广泛应用于飞行器、航天器、船舶以及车辆等的连接结构中。
1 考虑弹性连接的结构固有频率
设整体结构是由P 和Q 两个子结构组成,且两个子结构间为n 个参数相同但相互独立的弹性连接(即pi~qi,i=1,2,…,n),则具有弹性连接的整体结构示意图如图1 所示。

图1 整体结构示意图
通常情况下,根据CMS 中子结构的划分原则,可将图1 所示的整体结构划分成P 和Q 两个子结构,二者的界面结点集分别为Pv和Qv,考虑到弹性连接刚度的影响,两个子结构界面节点自由度位移并不连续,无法直接利用CMS 对整体结构的动力学特性进行准确分析。为了解决这个问题,本研究将图1 所示整体结构划分成P、Q 和C 3 个子结构,其中C 为连接子结构,且令连接子结构C 只有界面结点,如下页图2 所示。连接子结构C 的划分,则可使界面位移协调条件得到满足。
待子结构划分完成后,根据CMS 的工作原理,首先按照内部结点自由度u 和界面结点自由度v 将主子结构P 和Q 的质量和刚度矩阵进行分块整理,即MP、KP和MQ、KQ,并在此基础上分别计算两个主子结构的假设模态集φP和φQ(由保留主模态和约束模态组成)[24]。

图2 子结构划分示意图
国内外学者在研究机械连接对整体结构动力学特性的影响时,通常忽略连接质量的影响,即令连接质量为零[22-23]。同时,上述提到可利用空间梁单元的刚度矩阵来等效弹性连接的刚度,因此,本研究利用零质量空间梁单元来对弹性连接进行等效。
空间梁单元的刚度矩阵Kb写为如下形式:

式中,Kb1为确定矩阵,其表达式参见文献[1],E 为弹性模量。
又由于连接子结构C 中的各个弹性连接相互独立,则根据式(2)可将连接子结构C 的刚度矩阵KC写为:

此外,由于空间梁单元只有界面结点自由度而无内部结点自由度,故弹性连接的假设模态集φC为:

基于上述分析结果,可获得整体结构的质量矩阵M、刚度矩阵K和模态矩阵分别如下形式:

设整体结构的位移列向量为X,即:
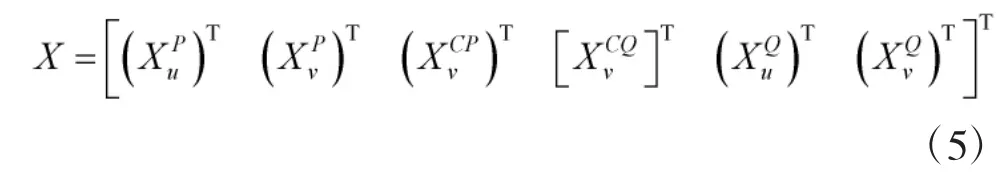
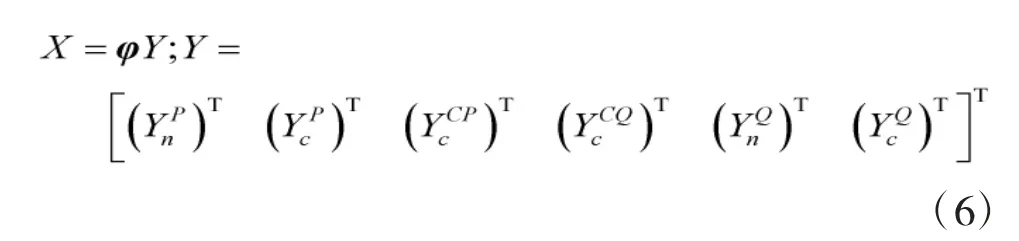
引入界面位移协调条件为:

式中,LP和LQ为坐标旋转变换矩阵。对式(4)~式(7)进行整理可得:

根据式(8)引入矩阵T对模态坐标Y 进行变换,如下所示:

式中,模态坐标Z 中各分块元素相互独立。与此同时,可得对应的模态参数矩阵分别为:
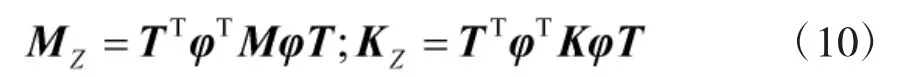
综上所述,基于CMS 建立的如图1 所示整体结构自由度缩减后的振动方程为:

则由瑞利商公式可得图1 所示整体结构的第i阶角频率ωi为:
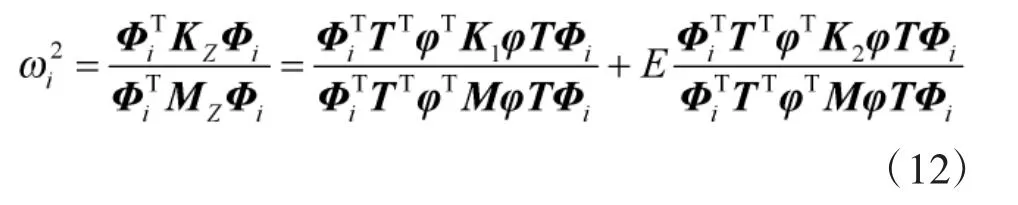
式中,Φi为式(11)所示振动方程的第i 阶模态矩阵,矩阵K1和K2均为确定矩阵,二者的表达式分别为:

2 考虑弹性连接的结构频响函数
考虑弹性连接的FBSM 是基于广义导纳方法推导获得,而在广义导纳方法的推导过程中要求把所有的子结构等效成一个子结构系统来进行处理,故由文献[20]可知,可利用图3 所示示意图对考虑弹性连接的FBSM 进行推导。
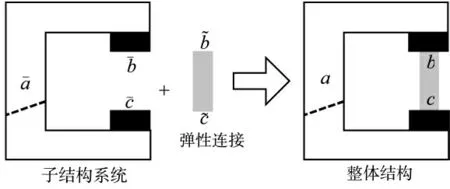
图3 考虑弹性连接的频域子结构方法的推导示意图
图3 中,顶标“-”和“~”为子结构系统和弹性连接,b 和c 为界面节点自由度,a 为内部节点自由度。据此可知,子结构系统的弹性连接的阻抗矩阵和频响函数矩阵为:

式中,x 和f 分别为响应和激励列向量,H 和Z 分别为频响函数和阻抗矩阵,H 为子结构系统的频响函数矩阵,ZC为弹性连接的阻抗矩阵。假设弹性连接的阻尼为瑞利阻尼,且考虑到MC=0,则可得ZC的表达式为:

式中,j 为虚数单位,β 为瑞利阻尼比例系数。
由于子结构综合前后其内部结点自由度未发生改变,则有:

引入考虑弹性连接的位移协调和力平衡条件如下:
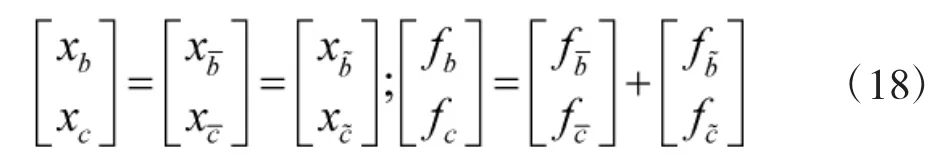
整理式(14)、式(17)和式(18)可得:

整理式(15)、式(17)和式(18)可得:

将式(20)代入式(19)并写成矩阵形式可得:
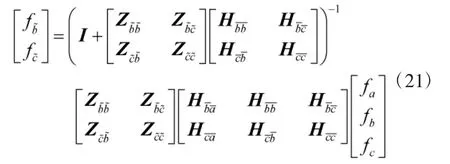
此时,将式(17)、式(18)和式(21)代入式(15),并进行整理即可获得考虑弹性连接整体结构的频响函数矩阵H:
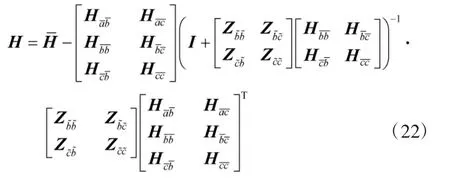
上述即为考虑弹性连接FBSM 的推导过程及结果。此外,文献[25-26]指出,若上式中的求逆矩阵为奇异矩阵,可利用奇异值分解方法对其进行处理,从而提高该方法的适用性。
3 考虑区间弹性连接的结构动力学特性
本研究将空间梁单元的弹性模量E 和比例阻尼系数β,设成区间参数以模拟弹性连接的区间不确定性。对区间参数的基本概念进行简单介绍,设G为区间参数,可写成如下形式:

式中,Gx和Gs分别表示区间参数G 的区间下限和上限。此时,根据IFM 可将区间参数G 写成其区间中心值Gc与区间因子Gi乘积的形式,即:

上式中,Gc和Gi的表达式分别为:

式中,δG 为区间参数G 的相对不确定量,其表达式为:

式中,ΔG 为区间参数G 的区间半径,其表达式为:

故由上述可得:

3.1 考虑区间弹性连接的结构固有频率
式(12)所示固有频率的表达式中,除弹性模量E 外,Φi也为区间参数,故可将Φi写成其区间中心值与区间因子乘积的形式,即:

将式(28)和式(29)代入式(12)并进行整理可得:

式中,ξi的表达式为:
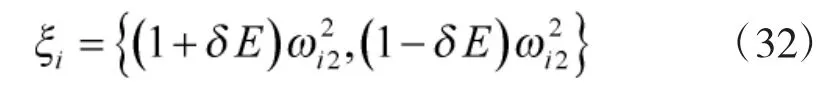
3.2 考虑区间弹性连接的结构频响函数
记e=1+jωβ,则e 也为区间参数,即可写为:

将式(2)、式(28)和式(33)代入式(16)并整理可得:
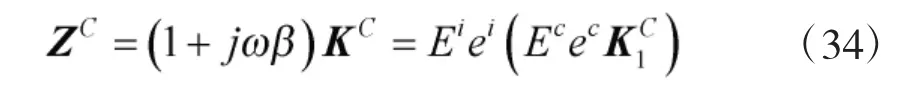
将式(34)代入式(22)并整理可得:
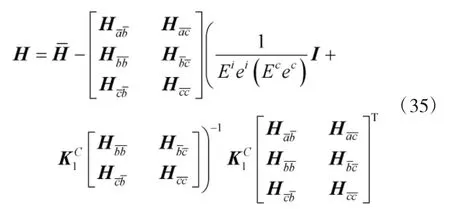
此时,根据区间分析方法,可得考虑区间弹性连接的结构频响函数幅值的区间下限和区间上限分别为:

式中,ξ 的表达式为:
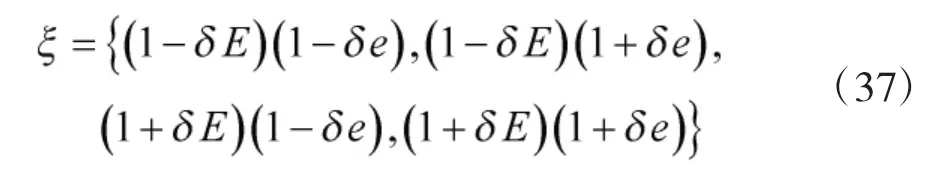
4 仿真验证
为了验证CMS-IFM 和FBSM-IFM,本研究设计了一个梁结构,如图4 所示。其中,矩形截面梁P 和Q 的材料参数和几何尺寸相同,阻尼均为瑞利比例阻尼,两根梁的参数均为确定参数;C 为两根参数相同的圆形截面梁,其密度设为0,弹性模量和瑞利阻尼比例系数为区间参数,用来模拟区间弹性连接。利用空间梁单元对梁结构进行单元划分,并定义单元属性[27-28],其中,表1 为连接子结构C 的单元属性,表2 为主子结构P 和Q 的单元属性。

图4 梁结构示意图
分别利用CMS-IFM 和FBSM-IFM 对梁结构的固有频率和指定结点频响函数幅值的区间下限和上限进行了计算,同时利用Monte-Carlo 模拟方法开展了相应计算。在利用CMS-IFM 计算时,保留子结构P 和Q 的前30 阶主模态参加模态综合;在利用FBSM-IFM 开展计算时,选用子结构P 和Q 的前30 阶模态进行各自频响函数矩阵的计算,计算方法参见文献[27]。在利用Monte-Carlo 模拟方法进行计算时,假设两个区间参数E 和β 在其分布区间内都呈均匀分布,然后生成5 000 个样本,并分别代入整体结构的有限元模型中进行计算(即共计算5 000次),最后从5 000 个计算结果中选取固有频率和频响函数的区间下限和上限。

表1 连接子结构C 的单元属性

表2 主子结构P 和Q 的单元属性
表3 给出了利用CMS-IFM 和Monte-Carlo 模拟方法对算例结构固有频率区间下限和上限计算结果的对比情况。图5 给出了利用FBSM-IFM 和Monte-Carlo 模拟方法,对算例结构中两个结点u 和v 之间3 个平动方向频响函数幅值区间下限和区间上限的计算结果对比情况。
表3 中,CIx、CIs和MCx、MCs分别为CMS-IFM和Monte-Carlo 模拟方法对固有频率计算结果的区间下限和上限,εx和εs分别为CMS-IFM 对固有频率区间下限和上限的相对计算误差。不难发现,CMS-IFM 对固有频率区间下限和上限的相对计算误差分别在±0.586 %和±0.628 %以内,表明CMS-IFM 在保证计算精度的前提下,可有效提升计算效率。
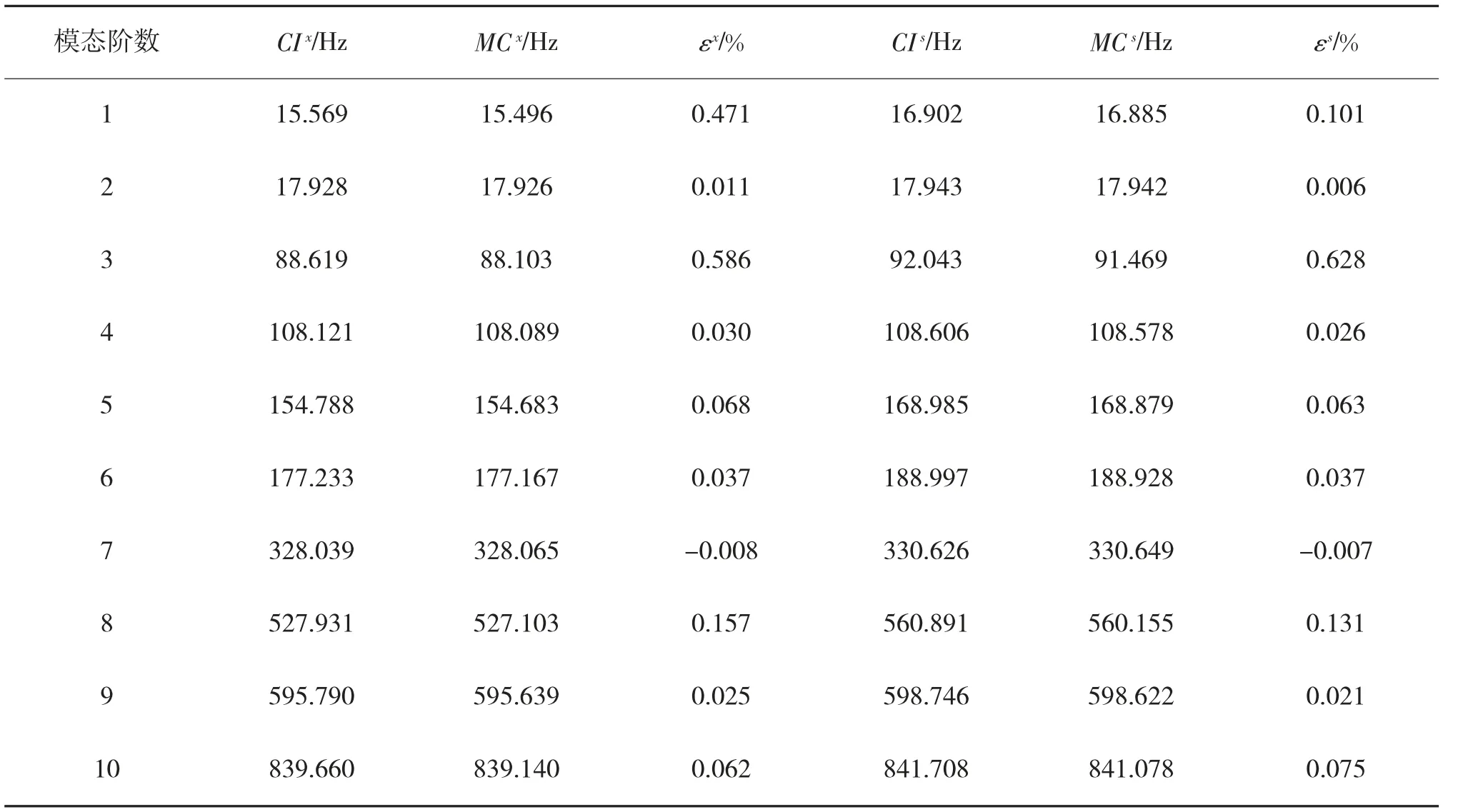
表3 CMS-IFM 和Monte-Carlo 模拟方法计算结果
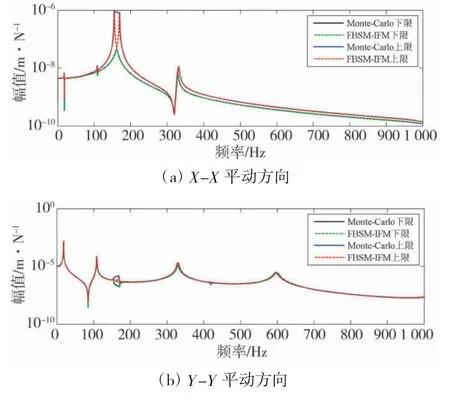

图5 不同平动方向两种方法计算结果的对比情况
由图5 可知,两种方法对图3 所示算例结构频响函数幅值区间下限和区间上限的计算结果吻合程度良好,验证了FBSM-IFM 的正确性。
5 结论
1)笔者利用具有区间弹性模量和比例阻尼系数的零质量空间梁单元模拟复杂结构中的区间弹性连接,基于CMS 和FBSM 对考虑弹性连接的结构固有频率和频响函数进行了推导,并结合IFM 提出了计算考虑区间弹性连接结构动力学特性的高效方法,即CMS-IFM 和FBSM-IFM。
2)该方法基于IFM 综合考虑弹性连接结构的区间不确定性,不仅可以单独考察某一区间不确定参数对结构动力学特性的影响,而且可以有效地规避区间参数,按照确定参数进行处理时可能得到矛盾的或很不合理的结果的问题。
3)算例仿真结果表明:与Monte-Carlo 模拟方法相比,CMS-IFM 和FBSM-IFM 在保证计算精度的同时,均可大幅提升计算效率,所得的结论具有较高的理论研究和工程应用价值。
