反舰导弹目标毁伤预测的贝叶斯推断模型研究

李 聪，关爱杰，陈 健，徐博奥

（解放军96901 部队，北京 100094）

0 引言

导弹反舰作战作为一种新兴的作战样式，可以有效起到反介入/区域拒止的战略战役效果，是一种典型的非对称打击手段。目标毁伤预测在导弹反舰作战中扮演着关键角色，它能定量刻画作战过程的各风险要素，指导如何以最小成本代价达成预定毁伤要求，是火力打击规划的重要一环。目标毁伤预测不同于目标毁伤评估，后者主要关注事后，评估目标在实际遭受打击后的物理或功能毁伤程度；而前者主要关注事前，即在给定打击武器型号、性能和数量的前提下，预测特定目标将会遭受的毁伤水平。目标毁伤预测研究对于作战辅助决策、作战运用研究和装备体系建设等问题具有重大的理论和现实意义。

目前，主要有两种技术方法可用于反舰导弹目标毁伤预测［1-5］：1）在系统级和机理级上，建立反舰导弹（包括弹体、战斗部、导引头等）和目标舰船（包括船体、动力系统、反导系统等）以及关于它们之间在探测、突防、干扰、毁伤等物理层面相互作用的细粒度行为模型，通过数学解析方法或仿真模拟方法获得目标毁伤预测结论；2）基于实弹打击靶船试验数据，以导弹特征、目标特征、环境特征等要素为自变量，以目标毁伤程度为因变量，通过传统的模式识别和机器学习算法（如线性回归、支持向量机、深度学习等），建立两者之间的线性或非线性函数关系，在新的作战想定下，即可直接利用此函数关系求出目标毁伤程度。

然而，这些方法都存在一定程度的局限性。第一种方法为确保结果可信，要求对作战实体及实体间相互作用进行细粒度建模，然而粒度越细，计算代价越高，且对于敌方舰船，通常难以获得建模所需的详细信息；第二种方法采用的模式识别和机器学习算法一般需要大量样本数据作为支撑，但鉴于反舰作战在军事上和政治上的敏感性与特殊性，难以在特定成本约束下收集大量试验数据，样本量不足以支撑模型的充分训练。

近年来，贝叶斯网络技术［6-7］在军事领域获得了广泛应用，如效能评估［8］、威胁分析［9，12］、智能决策［10］和目标识别［11］等。贝叶斯网络可以简洁定量地描述随机事件间的因果关联关系，并有效融合多源信息对潜在变量进行概率推断，能够处理作战过程中的大量不确定性因素，且由于其本质上是一种贝叶斯方法，在合理设置先验信息的前提下，不需要大量样本支撑模型训练，在使用成本上有显著优势，故本文采用贝叶斯网络技术进行建模研究。

1 贝叶斯推断模型的建立

本节基于贝叶斯网络技术，建立用于反舰导弹目标毁伤预测的贝叶斯推断模型。此模型是一种一体化的解决方案，不仅解决了给定发射弹量下的目标毁伤预测问题，还充分发挥贝叶斯方法的优势，通过微调若干模型变量的设定，附带解决了满足特定成本约束与预定毁伤概率条件下的发射弹量规划问题，但两者核心均建立在同样的概率化目标毁伤预测过程的基础上。

下面首先讨论样本数据的准备以及目标打击构设映射，其次给出模型的数学描述及贝叶斯网络形式，最后提出模型推断策略。本文模型的使用条件需基于同型号反舰导弹。

1.1 样本数据准备

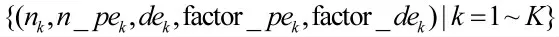
1.2 目标打击构设映射

此处定义目标打击构设为待打击舰船的大小、材质、航速和反导装置等特性在一次反舰作战中的设定。目标打击构设映射的目的是建立目标舰船与靶船基于各自的打击构设时，在反导能力和易损性上的定量对应关系。目标打击构设映射是模型进行目标毁伤预测的关键依据，因为除去反舰导弹本身的战术技术性能外，能决定毁伤效果的主要因素就是舰船的反导能力和易损性。这里，目标打击构设映射的建立需要计算目标反导能力映射因子和目标易损性映射因子。

首先，计算目标反导能力映射因子factor_pe，其衡量在各自的打击构设下，目标舰船相比靶船在反导能力上的倍数，计算时需要综合考虑软拦截（释放电磁或箔条干扰等）和硬拦截（使用拦截导弹或近防炮等）两种方式。这里定义factor_pe 为：

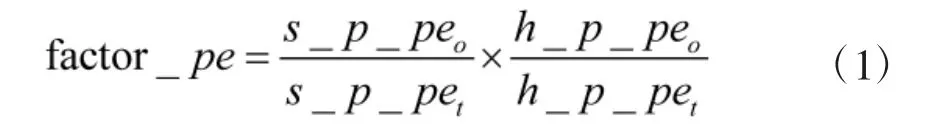
其中，s_p_peo和s_p_pet分别为在靶船和目标舰船的打击构设下，单枚导弹对软拦截方式的突防概率，h_p_peo和h_p_pet分别为在靶船和目标舰船的打击构设下，单枚导弹对硬拦截方式的突防概率。显然，factor_pe 值越大，目标舰船的反导能力越强，相应地，靶船的反导能力就越弱。

其次，计算目标易损性映射因子factor_de，其衡量在各自的打击构设下，目标舰船相比靶船在抗毁伤能力上的倍数，计算时需要综合考虑舰船的航速和材质因素。一般地，舰船航速越快，材料强度越高，就越难于毁伤。这里定义factor_de 为：

其中，vo和vt分别为靶船和目标舰船在各自打击构设下的逃逸航速，mo和mt分别为靶船和目标舰船在各自打击构设下的材料强度（单位：MPa）。显然，factor_de 值越大，目标舰船的抗毁伤能力越强，相应地，靶船的抗毁伤能力就越弱。

1.3 模型形式化描述

本文模型在概率语义层面描述了导弹反舰作战中的突防和毁伤等过程，包含3 个步骤：

第1 步，建立反舰导弹能力参数先验分布。具体地，需要建立反舰导弹总体能力ability、对目标舰船突防能力偏差pe_ability 和对目标舰船毁伤能力偏差de_ability 的先验分布。参数ability 表征反舰导弹在飞行、突防、毁伤等方面的综合性能水平，这是与具体打击目标无关的量。而参数pe_ability 和de_ability 是与具体打击目标相关的量，在模型中分别代表导弹打击目标舰船的能力相对导弹总体能力在突防和毁伤两方面的偏差量。反舰导弹能力参数先验分布及相关衍生参数的定义为：

第2 步，利用第1 步中的参数pp_pe 和pp_de建立目标舰船毁伤概率的产生过程，概率化表示如下：

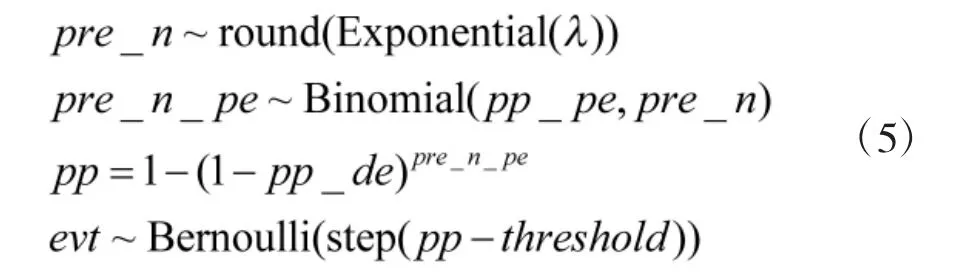
其中，Exponential、Binomial 和Bernoulli 分别代表指数分布、二项式分布和伯努利分布。round 函数为四舍五入取整函数，step 函数定义为：

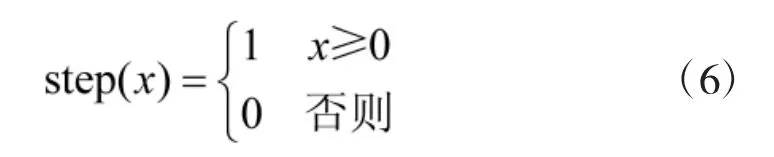
此外，pre_n 和pre_n_pe 分别是发射弹量和突防弹量，pp 是在有pre_n_pe 枚导弹突防情况下目标舰船的毁伤概率。pre_n 服从的指数分布刻画了发射成本，根据指数分布密度函数性质，发射弹量越多，对应概率密度越低，则成本越高，且分布参数越大，成本约束越严苛。evt 和threshold 用于发射弹量规划用途，分别代表事件发生标志和最低毁伤概率阈值，根据伯努利分布和step 函数的性质，可知当evt=1 时，必有pp≥threshold 事件发生，即evt=1 时必然满足目标毁伤概率不低于给定的阈值threshold。

第3 步，利用第1 步中的反舰导弹能力参数ability、pe_ability 和de_ability，以及靶船的目标打击构设映射因子factor_pe 和factor_de，建立K 次实弹打靶试验中突防和毁伤样本数据的概率产生过程，对任一打靶试验编号k（=1～K），概率化表示如下：

其中，tpe_abilityk和tde_abilityk分别为在第k 次打靶试验的打击构设下，单枚导弹打击靶船的突防能力偏差和毁伤能力偏差，它们映射自导弹打击目标舰船的突防能力偏差pe_ability 和毁伤能力偏差de_ability。易见，随着factor_pek或factor_dek的增大（或减小），tpe_abilityk或tde_abilityk也相应增大（或减小），以此达到了随着靶船的反导或抗毁伤能力的降低（或增强），导弹打击此靶船的突防或毁伤能力相应增强（或降低）的目的。参数p_ pek和p_dek分别代表单枚导弹打击靶船的突防概率和毁伤概率，nk、n_ pek和dek对应第k 次打靶的实采数据。pk是在有n_ pek枚导弹突防情况下靶船的毁伤概率。

下页图1 是本文建立的贝叶斯推断模型的贝叶斯网络形式，黑色圆点代表确定性变量，椭圆节点代表随机变量，其中，灰色背景节点对应打靶实采数据，实有向箭头表示变量间存在条件依赖关系，虚有向箭头表明变量的参数输入。

1.4 模型推断

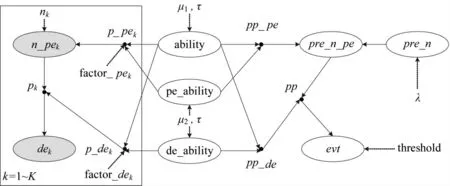
图1 模型的贝叶斯网络形式

模型推断的目的是在给定实弹打靶样本集时，计算模型中所关注的变量的分布，本质上这是贝叶斯后验推断过程［13］。在进行目标毁伤预测时，关注的是给定发射弹量下的目标毁伤概率，这时固定式（5）中的发射弹量pre_n，求出毁伤概率pp 的后验分布。不过，由于变量pp 的精确后验分布形式较为复杂，难以求出闭合形式解，故对模型使用Gibbs 抽样方法进行后验推断，用足量的抽样样本来逼近真实后验分布。进一步地，作为模型的附加功能，在进行发射弹量规划时，发射弹量pre_n 不再固定，而是作为一个随机变量，此时关注的是给定最低毁伤概率阈值下pre_n 的后验分布，需依据作战需求设置式（5）中的发射成本分布参数和最低毁伤概率阈值threshold，并设定evt=1，求出发射弹量pre_n 的后验分布，计算时同样使用Gibbs 抽样方法。

2 实验分析

2.1 模型运行设置

模型概率语义使用贝叶斯建模工具OpenBUGS编程实现，Gibbs 后验抽样样本数设为100 000。现假设进行了6 次导弹反舰打靶试验，且已知目标舰船的目标打击构设，收集到表1 的样本数据。在模型的目标毁伤预测模式下，实验选取不同的发射弹量pre_n，考查目标毁伤概率的分布和变化情况。在模型的发射弹量规划模式下，实验选取不同的指数分布参数和阈值threshold，考查最优发射弹量的变化情况。所有实验中统一设置模型先验参数和分别为1、0 和0.05。

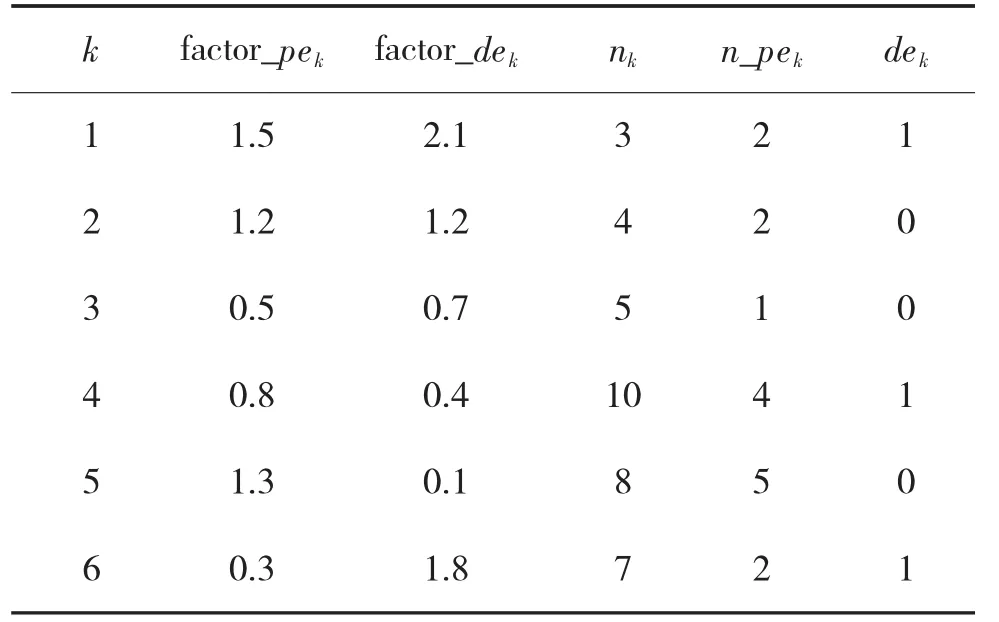
表1 实弹打靶样本数据

2.2 结果分析

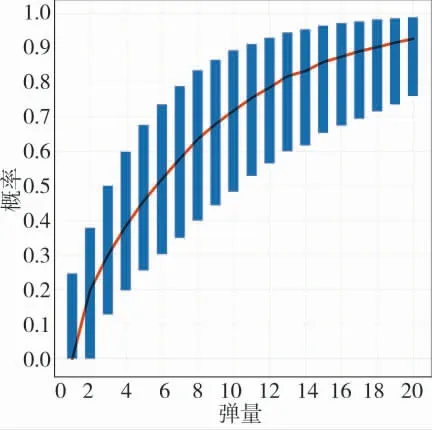
图2 不同发射弹量下的目标毁伤概率

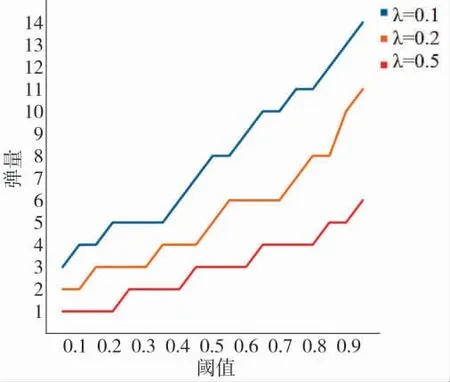
图3 不同毁伤概率阈值下的最优发射弹量

图2 为目标毁伤预测模式下发射弹量与毁伤概率的数量关系。图中的折线连接了每个发射弹量下目标毁伤概率后验分布样本的中位数（即50%分位点），且每个细长矩形的上下边沿分别为对应弹量下目标毁伤概率后验分布样本的75 %分位点（Q3）和25%分位点（Q1），所以矩形的长度代表四分位距（IQR），表征了后验分布样本的分散程度。从图中易见，随着发射弹量的增加，目标毁伤概率总体呈增加趋势，这是符合实际经验的。同时，IQR 总体呈现先增加后减少的趋势。在实际应用中，后验分布样本的中位数可作为目标毁伤概率估计值，但同时也要参考对应的IQR，IQR 越小，目标毁伤概率估计值越准确。不过需强调，图2 并不表示一种严格的函数关系，而且这里也未考虑导弹的发射成本，故不能从图中由毁伤概率反推最优发射弹量，仅可用于辅助考查给定发射弹量时目标毁伤概率的总体分布状况。

3 结论

本文提出了一种新的导弹反舰作战目标毁伤预测模型，此模型在建立目标舰船与靶船的目标打击构设映射的基础上，使用贝叶斯网络技术，定量描述了导弹打击靶船与目标舰船的突防及毁伤等数据的概率产生过程，并以少量的实弹打靶数据为基本依据，可一并对目标毁伤概率与最优发射弹量进行贝叶斯后验推断。此模型为导弹反舰作战的火力打击规划提供了新的思路与技术。未来的工作将致力于研究模型的变分推断方法。