IBAS-LMBP 神经网络算法在图像压缩中的应用*

王海军，金 涛，门克内木乐

（1.鄂尔多斯应用技术学院数学与计算机工程系，内蒙古 鄂尔多斯 017000；2.鄂尔多斯应用技术学院信息工程系，内蒙古 鄂尔多斯 017000）

0 引言

随着成像技术在军事、安防、地质、农业和医学等领域的广泛应用，大量高清图像随之产生，要快速传输和存储这些图像，就必须对图像信息进行有效的压缩处理。目前，常用的压缩方法主要有霍特林变换技术、离散余弦变换技术和小波变换技术。其中霍特林变换技术拥有如去相关性强、变换后能量集中程度高和可进行最优稀疏表示等优点，但由于运算量过大，且无快速算法，在实际工程中应用很少［1］。离散余弦变换技术具有实现的压缩率高、计算复杂度低、且实现较容易的优点，但是其方块效应破坏了子图像的相关性［2］。小波变换技术可以有效消除图像数据空间冗余，计算量也不大，但是小波变换只能进行方向上的变换，不能反映图像的结构和边缘特征,对于实现较大压缩比时图像质量下降明显［3］。基于此众多学者开始探索新的建模简单、易实现高压缩比、计算复杂度低的算法。神经网络具有极强的非线性处理能力和自适应能力，且建模简单，自然而然也成为图像压缩研究领域关注的重点，其中尤其以误差反向传播（Back Propagation，BP）神经网络图像压缩研究最为活跃［4-6］。但BP 神经网络采用的是梯度下降算法，存在对初始权阈值敏感易陷入局部极小值、收敛速度慢等问题［7］。

为了克服这些问题，常采用莱文伯格·马夸德（Levenberg Marquard，LM）BP 算法建模，相比梯度下降算法，LMBP 算法可以有效改善梯度下降算法收敛速度慢的问题［8］。但LMBP 算法是基于梯度下降算法的改进，因此，也存在初始权阈值敏感易陷入局部极小值问题。天牛须算法（Beetle Antennae Search，BAS）是2017 年由Xiang Y J.等人提出的一种新型的仿生算法［9］，已有研究表明，BAS 算法与遗传算法、粒子群算法等仿生算法一样，可以有效改善BP 神经网络对初始权阈值敏感、易陷入局部极小值问题［10］，但是BAS 算法在多维非线性优化问题求解时存在局部收敛问题，因此，本研究中通过分析BAS 算法的特点后，通过引入惯性权值，更新衰减系数，限定解位移区间构建改进天牛须搜索算法（Improved Beetle Antennae Search，IBAS），并将其与LMBP 算法结合建立IBAS-LMBP 算法模型。实验结果证明，与GA-LMBP、PSO-LMBP 及BAS-LMBP 算法模型相比，基于IBAS-LMBP 算法的图像压缩模型运行效率更高。

1 IBAS-LMBP 算法设计

1.1 训练算法选择

BP 神经网络寻优过程实质是求出所求问题的最小误差对应的解，其数学描述如式（1）所示：

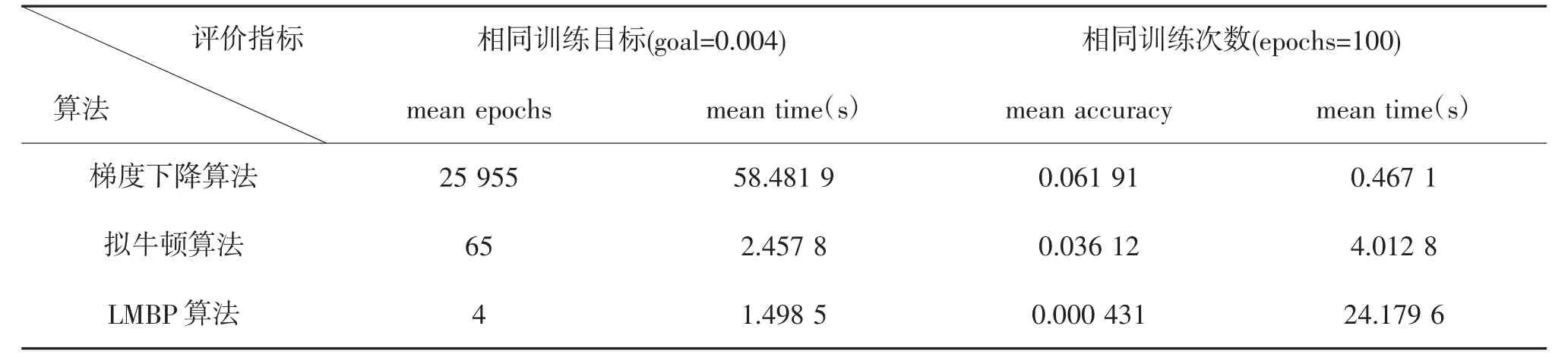
表1 基于不同训练算法的BP 模型性能比较

1.2 BAS 算法基本原理

BAS 算法是一种以天牛触须搜索食物行为衍生而来的一种仿生学算法，该算法基本原理是：天牛在觅食时，并不知道目标在哪里，它通过触须感知食物气味，根据气味浓度来确定搜寻目标位置。如一侧触须收到的气味浓度强于另一侧，下一步天牛就向气味浓度高的区域行进，在新位置继续判断气味浓度，如此反复，直到搜寻到气味浓度达最大值，即认为天牛已找到目标位置［13］。

根据以上仿生原理，采用以下3 条规则来抽象出如图1 所示的搜索算法中的简化天牛模型：

规则1：以天牛质心位置代表天牛位置，其触须位于质心左右两侧且距离相等；

规则2：天牛每步行进距离与左右触须间的距离比是固定常数；

规则3：在天牛每次到达新位置时，头的朝向是随机的。

图1 简化天牛模型

依据以上简化模型，则对于一个极小值优化问题，设优化函数为f（·），天牛须算法计算步骤如下：

Step 1 建立天牛须朝向的随机向量并将其表示为单位向量，如式（4）所示：

式中，rands（·）表示随机［0，1］之间的函数，q 表示搜索空间维度。

Step 2 确定天牛左右触须的位置。

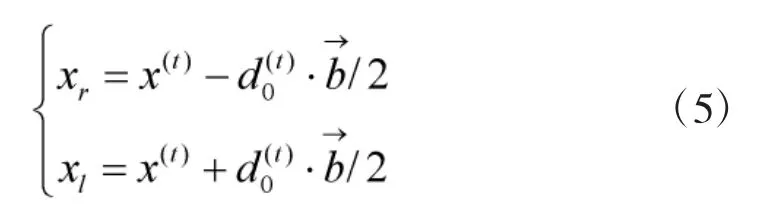
式中，xl表示左触须向量，xr表示右触须向量，x（t）表示在第t 次迭代时的质心位置，d（t）表示第t 次迭代时两须之间距离。

Step 4 对于步长step 和触须间距d0的计算，目前使用较多的是变步长和动态间距计算［11］，如式（8）、式（9）所示。

式中，δ 为步长的衰减系数，c 为间距系数。

Step 5 判断是否符合迭代结束条件，符合结束迭代，不符合重复Step 1～Step 4 直到符合条件。

与GA 和PSO 算法对比，BAS 算法只需要一只天牛，运算量小，运算速度快，但是在解决多维非线性优化时也存在易陷入局部最优问题，基于此设计如下IBAS 改进策略。

1.3 IBAS 改进策略

为了增加BAS 算法中天牛的寻优能力，对BAS算法作了如下几步的改进：

1）惯性权值的引入——算法初始阶段，较大的惯性权值可以使天牛扩大搜索范围，避免陷入局部最优，在算法运行后期，天牛接近最优解，此时较小的惯性权值可是天牛在当前最优解附近搜索接近最优解。参照PSO 算法，惯性权值的设计如式（10）所示。同时通过引入符合函数sign（·），将式（6）和式（7）两种情况合并，此时天牛质心计算公式变为如式（11）所示：

式中，φmin为初始惯性值，φmax为迭代至Tmax时的惯性值，φ（t）为第t 次迭代的惯性值。

2）衰减系数的计算——步长衰减系数δ 用来控制天牛的区域搜索能力，初期其取值应尽可能大，使天牛可以快速向食物移动，在后期放慢搜索进程，与惯性因子一起完成对步长移动的二次调节。在本文中对δ 采用式（12）所示的计算公式，此时天牛步长公式由式（8）变为式（13）：

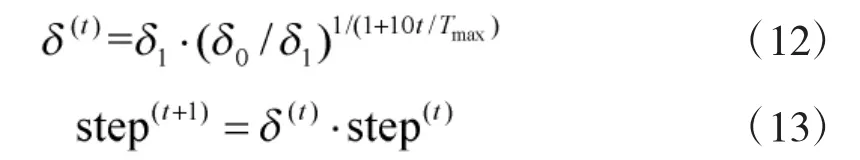
式中，δ1、δ0为步长调节系数，δ（t）为t次迭代的衰减系数。

1.4 IBAS-LMBP 算法步骤设计

IBAS 优化LMBP 神经网络的核心思想是：在IBAS 算法运行中，将IBAS 算法的欲寻优变量（天牛的初始位置）设置为神经网络的初始权阈值组合，在IBAS 算法运行过程中仅以适应度函数作为评估天牛行进的标准，在本文中以食物散发的气味浓度即训练样本均方误差作为IBAS 算法所求适应度函数，如式（14）所示。IBAS 算法通过左右触须不断探测食物气味浓度调整行进方向的过程，就是调整LMBP 神经网络权阈值的过程，直到最终算法停止运行，具体实现步骤如下所示：

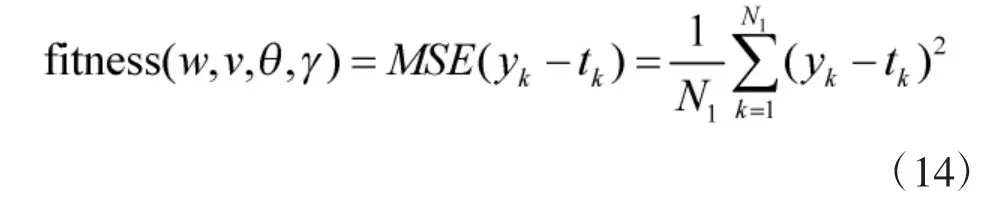
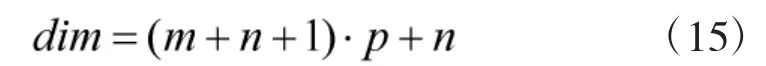
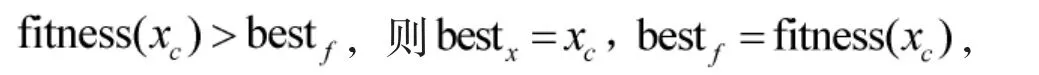
Step 3 迭代停止判断——判断当前适应度函数值是否达到设定精度（bestf＜0.001）或迭代进行到最大次数（Tmax＞100），如果满足条件则Step 4，否则，返回Step 2 继续迭代。

Step 4 最优解生成——在满足迭代停止条件时，bestx中的解即为BAS 算法训练得到的BP 模型初始最优权阈值组合，将上述最优解带入BP 神经网络中采用LMBP 算法进行二次训练，直到达到BP模型训练精度，形成图像压缩模型。

2 压缩模型设计

2.1 输入输出变量设计

图2 图像分块示意图

根据以上所述基于分块思想的图像划分方式，如果将一个128×128 像素图像，采用4×4 子像素块进行划分，此时BP 网络输入就可由128 降为16，网络结构大为简化，网络复杂度降低，从而为采用BP 神经网络进行有效图像压缩提供可行性和便利性。同时由于BP 神经网络激活函数tansig 和purelin 对输入数据比较敏感，因此，对分块后的数据采用式（16）进行归一化处理。式中，pmax和pmin为待处理图像数据的灰度域值，qmax和qmin为变换域值，pc为待处理的像素灰度值，qa为处理后的像素点值。

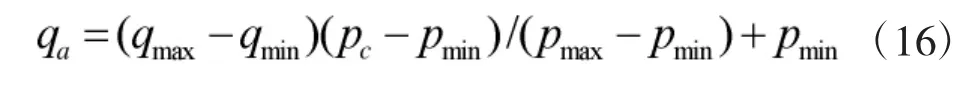
2.2 基本结构设计

在采用BP 神经网络进行图像压缩时，基本思想是把一组输入模式通过少量隐含层结点映射到一组输出模式，输出模式尽可能与输入模式相等。当隐含层结点数少于输入层结点时，就意味着隐含层能有效地表现输入模式，并将其传送到输出层。映射过程包含压缩编码和解码重建两个阶段，其中输入层与隐含层的变换看作图像的压缩编码阶段；而隐含层与输出层的变换看作图像解码重建阶段［12］。基于这一基本思想得到BP 模型输入层与输出层结点数相等，即inputnum=outputnum。在图像压缩时，BP 神经网络用于图像编码的压缩比K与输入层结点数inputnum 和隐含层结点数hiddennum 有关，其具体计算公式如式（17）所示［13］，图3为压缩比K=2 时采用的BP 模型基本结构。

K=inputnum/hiddennum（17）

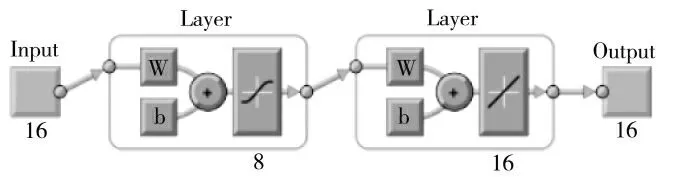
图3 压缩比为K=2 时的BP 模型基本结构

3 实验分析

为了验证本文提出的IBAS-LMBP 算法在图像压缩研究中的有效性，采用GA-LMBP、PSO-LMBP、BAS-LMBP 及IBAS-LMBP 算法建立图像压缩模型，并用峰值信噪比（PSNR）对模型重建图像评价。采用128 pixel×128 pixel Lena 图像作为训练样本，128 pixel×128 pixel Cameraman 图像作为测试样本，128 pixel×128 pixel Brain 图像作为验证样本。图4～图6 为采用各种算法对压缩比K=2 的模型进行图像重建的结果，从图像直观地看出，各种算法的重建图像效果差别不明显，主观看几种算法重建效果都不错。

图4 各种算法的Lena 重建图

图5 各种算法的Cameraman 重建图

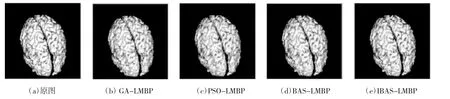
图6 各种算法的Brain 重建图

下页表2 和表3 分别给出了压缩比K=2 和K=4 时的PSNR 对比结果。可以看出，在压缩比K=2即模型结构为16-8-16 时，由于BP 模型权阈值参数数量较多，因此，随机数较多，此时无论是对训练图像Lena 还是测试图像Cameraman 及Brain，经过IBAS-LMBP 训练的模型PSNR 值明显好于GA-LMBP、PSO-LMBP 和BAS-LMBP。而在压缩比K=4 即模型结构变为16-4-16 时，BP 模型权阈值参数大幅度减少，模型的隐含层结点数也相应减少了，此时BAS-LMBP 算法运行的效率就不能保证都好于GA-LMBP 算法和PSO-LMBP 算法，而本文提出的IBAS-LMBP 算法依然是4 种算法中重建图像PSNR 最高的，因此，不论是在哪种结构模型下，IBAS-LMBP 算法都是运行效率最高的。在对仿生算法进行比较时，除了比较压缩算法重建效果，考虑算法性能时有必要进一步考查其运行时间，表4 给出了基于不同仿生算法进行权阈值初级寻优的时间，可以直观地看出，IBAS 算法无论是在哪种压缩比下，其运行时间都和BAS 相当，比GA 算法和PSO 算法明显快得多。

表2 K=2 时基于不同算法的压缩模型重建图像PSNR 评价（单位：dB）

表3 K=4 时基于不同算法的压缩模型重建图像PSNR 评价（单位：dB）

表4 4 种仿生算法运行时间对比（单位：s）

4 结论

本文在对BAS 算法运行整理流程进行分析后，为有效克服BAS 算法在对多维非线性优化问题求解时存在的易陷入局部极小值问题，通过引入自适应惯性权值，对衰减系数重新设计，同时设定天牛位置的取值即问题求解空间上、下限建立了IBAS算法，并构建IBAS-LMBP 算法图像压缩模型，利用IBAS 算法对BP 模型进行权阈值初次寻优，然后利用LMBP 算法对得到的初级结果进行二次寻优。最终的实验表明，本文的设计是成功的，IBAS 算法对LMBP 算法模型的优化效果明显好于GA 算法、PSO算法和BAS 算法，最终建立的压缩模型在保证高精度的同时还兼顾了速度。同时也进一步拓宽了仿生算法的应用范围，为研究神经网络图像压缩提供了一种新的思路。