基于确定性拥挤的多模态郊狼优化算法*

陈丹妮，赵剑冬，高 静

(1.广东技术师范大学计算机科学学院，广东 广州 510665；2.广东恒电信息科技股份有限公司，广东 广州 510630)

1 引言

多模态优化问题[1]是指优化的问题存在多个局部或者全局最优解，它普遍存在于我们的生活中，例如图像分割、机械设计和电力系统规划等。目前，群智能优化算法是解决多模态优化问题较为流行的一类方法。遗传算法GA (Genetic Algorithm)[2]、模拟退火SA (Simulated Annealing)算法[3]、粒子群优化PSO (Partical Swarm Optimization) 算法[4]、蚁群优化ACO (Ant Colony Optimization) 算法[5]、萤火虫算法FA (Firefly Algorithm)[6]、布谷鸟搜索CS (Cuckoo Search) 算法[7]、蝙蝠算法BA (Bat Algorithm)[8]、灰狼优化GWO (Grey Wolf Optimizer) 算法[9]、多元宇宙优化MVO (Multi-Verse Optimizer)算法[10]等群智能优化算法均是模拟自然界的现象规律或者生物种群的社会生活而提出的。Salcedo-Sanz[11]通过对大量群智能优化算法的研究，发现优化算法想要取得良好表现的基础是在勘探和探索之间取得平衡。而上述算法在优化过程中较少关注勘探和探索两者间的平衡，这可能限制了它们在多模态问题上的寻优能力。为了弥补上述不足，学者们提出了不少改进方法[12 - 16]，包括混合算法、环拓扑、局部信息和小生境技术等。

Pierezan等[17]受郊狼对生存环境的适应性及其社会结构的启发，在2018年提出了郊狼优化算法COA (Coyote Optimization Algorithm)，该算法为在优化过程中平衡探索和勘探提供了新的机制。郊狼优化算法能有效地处理具有边界约束的连续变量全局优化问题。然而，在现实世界中很多优化问题是多模态的，为了找到多模态问题的全局最优解，要求算法具有跳出局部最优的能力。在多模态情景下，郊狼优化算法的收敛精度和稳定性需要进一步提高。在此基础上，受到小生境技术对其他群优化算法的应用效果启发，本文提出了一种基于确定性拥挤的多模态郊狼优化算法DCCOA(Deterministic Crowding Coyote Optimization Algorithm)，旨在提高算法的收敛精度和稳定性。

本文的其余部分组织如下：第2节主要介绍郊狼优化算法和小生境技术的相关工作； 第3节详细介绍本文提出的基于确定性拥挤的多模态郊狼优化算法；第4节对实验结果进行理论分析；第5节给出结论和未来的研究工作。

2 相关工作

2.1 郊狼优化算法

COA算法将郊狼的生存环境状况视为优化问题的变量，将郊狼对环境的适应能力作为优化目标。郊狼根据郊狼群组内的信息共享和不同郊狼群组间的信息交流更新自身对社会状况的认知，各个郊狼群组经过多代郊狼的出生、交流、成长和死亡的更新迭代之后，整个郊狼群中环境适应能力最强的郊狼将被作为优化问题的最优解。COA算法与GWO算法不同的是：GWO算法关注狼群的社会等级和捕猎过程，而COA算法则将关注点聚焦在郊狼之间的交流和社会结构方面。

在国外，Güvenç等[18]将COA算法应用于风力发电的经济调度问题上，结果表明郊狼优化算法比遗传算法和粒子群优化算法具有更低的燃料消耗和更好的性能。此外，Qais等[19]使用COA算法建立了高精度的三极管光伏模型。与此同时，Pierezan等[20]将文化算法的一些概念引入COA中，提出了文化郊狼优化算法，并将该算法应用于重型燃气轮机的运行。上述研究都将COA算法应用于各种不同的实际问题。在国内，张新明等[21]提出嵌入全局引导和相互作用的郊狼优化算法，提升了COA算法的全局搜索能力，并应用于医学图像增强中的参数优化问题。此外，张新明等[22]还提出强化最优和最差狼的郊狼优化算法，通过引入全局最优郊狼引导操作，并且在最优郊狼的成长过程中嵌入一种随机扰动，提升了算法的全局寻优能力。与现有的群智能优化算法相比，COA算法具有过程简单、需要设定的参数较少等优点。但是，面对多模态优化问题时，COA算法的全局寻优能力不足，收敛精度和稳定性还有待提高。

2.2 小生境技术

1995年，Mahfoud[23]首次提出小生境技术，旨在促进遗传算法形成并维持稳定的亚群体。目前，小生境技术[24 - 26]主要包括适应度共享、物种形成、拥挤和清除等方法。其中，适应度共享、物种形成和清除方法都需要设置小生境参数，而且这些参数的设置需要先验知识。 拥挤方法是最早也是最简单的小生境技术之一，包括原始拥挤OC (Original Crowding)方法[24]、确定性拥挤DC (Deterministic Crowding)方法[23]和概率拥挤PC (Probabilistic Crowding)方法[27]。 其中，确定性拥挤方法因为不需要任何小生境参数，而更受欢迎。确定性拥挤DC方法随机选择2个个体作为父代(P1和P2)，随后生成2个新生子代(C1和C2)。在子代替换父代之前，DC方法综合考虑子代与父代彼此之间的距离和适应度。因此，本文将确定性拥挤方法引入COA算法中。

Thomsen[28]在差分算法DE(Differential Evolution)中分别使用了适应度共享方法(SharingDE算法)和确定性拥挤方法(CrowdingDE算法),实验结果表明，CrowdingDE算法具有更好的稳定性和收敛速度。为了解决多模态问题，Majumdar等[29]在入侵杂草优化算法中引入了拥挤技术，结果表明该算法比其他标准多模态优化算法具有更优的收敛精度。除上述文献之外，还有许多群智能优化算法[30 - 33]使用DC方法来提高算法的收敛精度，跳出局部最优，保持多样性等。郊狼优化算法也属于群智能优化算法。为此，本文提出了一种基于确定性拥挤的多模态郊狼优化算法(DCCOA)，旨在提升算法在多模态问题中的全局寻优能力。

3 多模态郊狼优化算法

基于COA算法，DCCOA算法有3个核心的改进部分：(1)新的郊狼进化机制；(2)新的郊狼群组文化趋势计算方法；(3)郊狼更新社会状况认知的新方法。DCCOA算法的流程如图1所示。

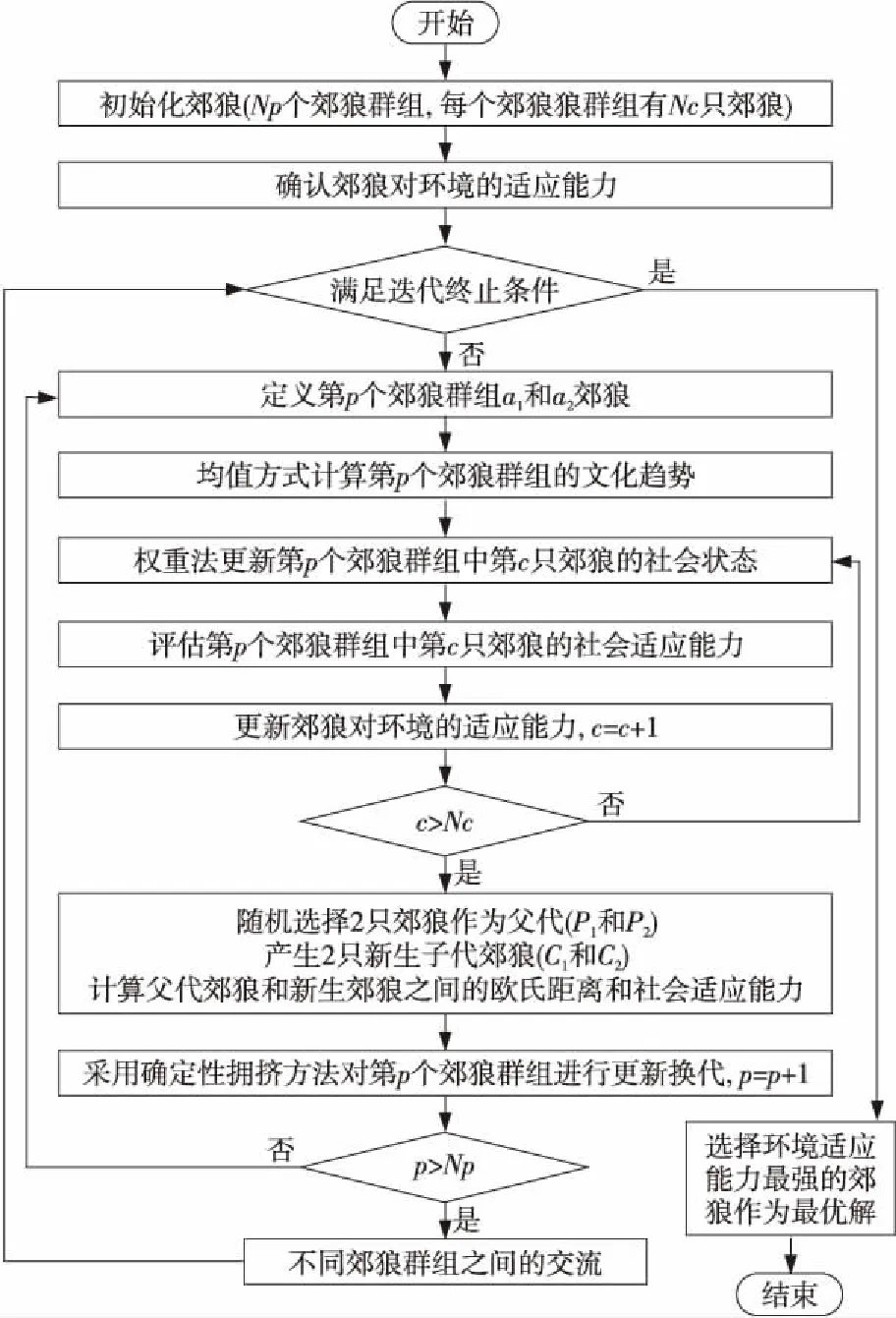
Figure 1 Overall of DCCOA

3.1 新的郊狼进化机制

在COA算法中，每代中每个郊狼群组只产生一只新生郊狼，而且这只新生郊狼能否存活取决于该郊狼群组中其他郊狼对环境的适应能力是否低于该新生郊狼。 然而，DCCOA算法采用确定性拥挤方法改进郊狼的进化机制。具体的步骤如下所示：

(1)从每个郊狼群组随机选择2只郊狼作为父代，记为P1和P2。

(2)在P1和P2郊狼和生活环境的影响下，产生2只新生郊狼作为子代，记为C1和C2。

(3)计算P1、P2、C1和C2郊狼对环境的适应能力，记为f(P1)、f(P2)、f(C1)和f(C2)。

(4)根据式(1)计算父代和子代郊狼之间的欧氏距离，记为EdP1C1、EdP1C2、EdP2C1和EdP2C2。

(5)根据父代郊狼和子代郊狼的适应能力和欧氏距离，采用确定性拥挤方法更新郊狼群组。

D维空间中，第b只郊狼的位置是Xb=(xb1，xb2，…,xbD)T，第d只郊狼的位置是Xd=(xd1，xd2，…,xdD)T，那么第b只郊狼和第d只郊狼之间的欧氏距离[34]为：

Edbd=‖Xb-Xd‖,b,d∈N

(1)

在新的郊狼进化机制内，只有在竞争的子代郊狼具有更好的环境适应能力情况下，它才能代替父代郊狼。 确定性拥挤方法是郊狼进化机制中的一个重要过程，它不仅保证了适应环境能力较强的新生郊狼得到存活，还确保了距离更接近的父代郊狼被存活的新生郊狼取代，以此来提升算法在多模态问题中的全局寻优能力。

3.2 新的郊狼群组文化趋势计算方法

除了提出新的郊狼进化机制，DCCOA算法还改进了郊狼群组文化趋势的计算方法。COA算法把每个郊狼群组中所有郊狼对环境适应能力的中位数作为该郊狼群组的文化趋势。 虽然中位数有着不容易受到极端值影响的优点，但它并不能全面地反映总体情况。算术平均值是由总体数据计算得出的，它具有优良的数学性质，是实际应用中使用最广泛的趋势测量方法。本文考虑到在郊狼群体生活中，每只郊狼都会对其群组的文化趋势有所影响，因此定义郊狼群的文化趋势计算方法如式(2)所示：

(2)

3.3 郊狼更新社会状况认知的新方法

对于郊狼这个物种而言，每个郊狼群组中通常有2只阿尔法郊狼(α)，然而COA算法在每个郊狼群中只定义了1只阿尔法郊狼。为了更真实地模拟郊狼物种的社会生活，DCCOA算法在每个郊狼群组中定义了2只阿尔法郊狼(α1和α2)，它们是在每个郊狼群组中对环境适应能力最强的2只郊狼。考虑到最小化问题，在t时刻第p个郊狼群的α1和α2定义如式(3)和式(4)所示：

(3)

(4)

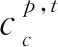
(5)

其中，ω1和ω2分别表示阿尔法郊狼α1和α2在其郊狼群组中对δ1的影响权重。经过多次调参实验测试，ω1和ω2的值设为0.8和0.2时效果最优。

此外，COA算法在更新郊狼对社会状况的认知时，设定阿尔法郊狼的影响(δ1)和郊狼群组文化趋势的影响(δ2)是随机的。然而，在郊狼种群的社会生活中，这两者的影响权重并非随机数。一般来说，阿尔法郊狼是每个郊狼群组中的强者，它们在郊狼更新对社会状况的认知过程中有着较大的影响，而郊狼群组的文化趋势影响则是潜移默化的，因此，在本文算法中，郊狼更新社会状况认知的方式如式(6)所示：

(6)

其中，λ1和λ2分别表示δ1和δ2的影响权重。经过多次实验测试，λ1和λ2的值设置为0.7和0.05时效果最佳。这也意味着在郊狼更新对社会状况认知时，相比郊狼群组的文化趋势影响，阿尔法狼有着更大的影响权重。

4 实验对比

4.1 实验设置与基准函数

为了评估本文提出的DCCOA算法的性能，将其与COA、PSO、GA、FA、CS、BA和MVO算法进行不同决策变量维数的多次实验对比。其中根据文献[17]将DCCOA和COA的参数Np和Nc分别设置为20和5，即郊狼总数为100。其他算法直接使用相应文献设定的参数。实验选择了8个典型的基准函数，具体如表1所示。为了验证算法在多模态问题中的全局寻优能力，8个基准函数包含2个单峰函数(F1和F2)和6个多峰函数(F3～F8),其中函数表达式中的n表示决策变量维数。

Table 1 List of benchmark functions used in the experiment

在上述基准函数上，8个算法分别在10维、50维和100维这3个不同决策变量维数上各独立进行50次实验。其中，当决策变量的维数为10维、50维和100维时，各算法的迭代次数分别为1 000次、2 000次和3 000次。实验的硬件环境为：Intel(R) Core(TM) i5-4210U CPU @ 1.70 GHz,4 GB内存。软件环境为：64位的Windows 10，Python 3.7.0。

实验采用最小值、最大值、均值和方差这4个指标来衡量算法的性能。其中最小值和最大值分别代表在50次实验中各算法能够找到函数全局最优解的最好表现和最差表现；均值代表50次实验中各算法的平均表现；方差代表各算法在实验中的稳定性。

4.2 性能评估与理论分析

表2汇总了在不同决策变量维数下，8个算法在基准函数上的收敛精度和稳定性的统计结果，其中，对最佳结果进行加粗显示。实验结果表明，在3个不同的决策变量维数上，DCCOA算法在多个基准函数上的性能均优于COA算法的。DCCOA算法表现出更好的收敛精度和更强的稳定性，最优表现时将收敛精度和稳定性提高了4个数量级。

从收敛精度的角度来看，总体上，在多模态函数上DCCOA算法的表现更佳，在单模态函数上FA、CS和PSO算法的表现较优。对于F1函数，当决策变量维数为10时，DCCOA算法的收敛效果是最好的，这是因为在较低维数下，将平均值作为文化趋势更有效地体现了每个郊狼群组中所有郊狼对社会状况的认知对该郊狼群组的文化趋势都有所贡献。但是，随着维数的上升，它的性能有所下降，此时，FA算法和CS算法的表现更胜一筹。这是由于布谷鸟搜索算法采用了随机游走的莱维飞行操作和萤火虫采用了相对亮度的引领操作，这让它们在高维数的连续单模态曲面有更好的收敛精度。对于F2函数，PSO算法的表现较佳，这是因为粒子群体在寻优过程中会将历史最优位置进行记忆并传达给其他粒子，这让其在单模态函数上具有较大的优势。这一优势也让PSO算法在低维数的多模态F6函数上具有良好的表现。对于F3～F8函数，DCCOA算法展示出了很好的收敛效果，尤其在高度多模态F5和F7函数上以及搜索难度较大的F8函数上，它的收敛精度优于其他几个算法。这是因为小生境技术的引入，进一步促进算法在寻优过程中平衡勘探和探索，从而提升算法跳出局部最优的能力。同时，更新郊狼对社会状况认知的新方法更真实地模拟了郊狼的种群生活，也有利于更好地寻找全局最优解。

从稳定性的角度来看，CS算法在单模态F1函数上展示出了较强的稳定性。这是因为布谷鸟算法在光滑曲面上通过不断随机行走可以逐步接近全局最优解。在单模态F2函数上PSO算法具有较佳的稳定性。这是因为粒子在优化过程中充分利用自身信息和群体信息，在求解单模态问题时具有优异特性。对于多模态F3～F8函数，DCCOA算法表现出较强的稳定性，这是由于新的郊狼进化机制采用了确定性拥挤方法，它不仅保证了适应环境能力较强的新生郊狼的存活，而且还确保离新生郊狼较近的父代郊狼被替代，有利于维持郊狼的多样性，提升算法在多模态问题上的稳定性。同时，新的更新郊狼对社会状况认知的方法采用权重法和定义2只阿尔法郊狼，这都更符合郊狼的真实种群生活，对算法稳定性的提升有所贡献。此外，FA算法在F4函数上也展现了较好的稳定性，这是由于在更新萤火虫时同时考虑了确定性因素和随机因素。

从收敛曲线的角度来看，整体上，BA算法和PSO算法最容易陷入问题的局部最优解，与此同时，BA有着更快的收敛速度；DCCOA算法和COA算法的表现相对稳定。在单模态函数上，8个算法在较低决策变量维数的表现没有太大的差异，但是随着维数的上升，PSO算法的性能有明显下降。在多模态函数上，PSO算法跳出局部最优的能力较差，这是因为它在寻优过程的勘探和探索之间没有取得平衡。BA算法虽然展示出了较快的收敛速度，但是它同样容易陷入问题的局部最优解。相比COA算法，DCCOA算法在大多数情况下展示出稍快的收敛趋势和较优的收敛精度。这是因为新的郊狼进化机制采用了确定性拥挤方法，它有利于进一步促进算法在勘探和探索之间的平衡，从而提升算法在多模态问题中的全局寻优性能。

5 结束语

为了解决多模态优化问题，本文提出了一种基于确定性拥挤的多模态郊狼优化算法(DCCOA)。该算法对COA算法做了3方面的改进，具体包括新的郊狼进化机制、新的郊狼群组文化趋势计算方法和郊狼更新对社会状况认知的新方法。为了评价DCCOA的性能，将其与COA、PSO、GA、FA、CS、BA和MVO算法在多个基准函数上进行实验。实验结果表明，相比COA算法，本文算法展示出更高的收敛精度、更快的收敛速度和更强的稳定性。本文证明了将确定性拥挤方法应用到郊狼优化算法上可进一步提升算法在勘探和探索之间的平衡能力，从而提升算法在多模态情况下的全局寻优能力。这是因为在更新郊狼群时，距离相近并且对环境适应能力较差的郊狼被淘汰。然而，本文还存在许多局限性，其中之一就是算法的计算时间相对较长。因此，在之后的工作中，将打算用平行策略进行搜索，以缩短算法寻优时间。

Table 2 Experimental results of eight algorithms on benchmark functions

续表