基于时态边缘算子的时间序列自主分段表示法*
2021-06-25殷炜宏王若愚段倩倩李国强
殷炜宏,王若愚,段倩倩,李国强
(1.上海工程技术大学电子电气工程学院,上海 201620 ;2.上海交通大学软件学院,上海 200240)
1 引言
近年来,数据量日益增长,数据中隐藏着许多有价值的信息,需要通过数据挖掘[1]来探究数据中隐含的有用信息。那么,在数据挖掘领域中,时间序列则是数据挖掘的一个热门研究领域[2]。时间序列作为一种特殊的大数据,普遍存在于金融、医疗、农业、气象、科学观测和工程等各个领域。若将原始数据直接用于时间序列的数据挖掘任务[3]中,则会导致过多的噪声被引入,使得实验结果往往较差,影响最终的度量精度。
因此,许多研究者提出了时间序列的表示方法,为后续的相似性搜索[4,5]工作做了很好的铺垫。现阶段,时间序列表示方法主要有4种[6]:频域表示法(离散傅里叶变换DFT(Discrete Fourier Transform)[7]和离散小波变换DWT (Discrete Wavelet Transform)[8])、奇异值分解SVD(Singular Value Decomposition)表示法[9]、符号近似聚合SAX(Symbolic Aggregate Approximation)表示法[10]和分段线性表示法PLR(Piecewise Linear Representation)[11]。
很多应用领域更关注时间序列在某个时间段的变化模式和规律,而不是单点特征。例如在医疗领域中,心电时间序列[12]在同一周期内会有不同的波段特征,如P波、PR间期、QRS波群、ST段等,这些波段间期有着各自的序列趋势特征,若从单点特征看是很难看出其属于哪个波段,而通过时序的表示方法能很清楚地看出每个波段的趋势特征,能更准确判断出该波形属于哪类波段,进一步确诊病人的心脏疾病。
在上述时序表示方法中,时间序列的分段线性表示方法简单直观且数据压缩效率高。该方法能够找到原序列上的某些特征点,并利用点与点之间一系列连续、首尾连接的直线段来近似表示时间序列,是一种数据降维和降噪的常见时序表示方法。因此,该方法得到了众多研究者的重视。
然而,寻找一种合适的分段线性表示方法并非易事。近年来,研究人员已经提出了一系列分段算法。目前,分段线性表示方法主要有2种,一种是由Keogh等[13]提出的采用拟合误差的方法进行分段表示,其主要思想是使得原始序列与拟合序列之间的残差平方和最小。而孙志伟等[14]提出的分段算法也是首先考虑拟合误差,并针对优先级较高的分段进行预分段,同时在分段时考虑最大、最小值点,从而提高了固定点分段效率。尽管这种自底向上的算法分段效果好,但时间复杂度较高,且不支持在线分段。另一种表示方法则是考虑全局约束值和寻找重要点。如文献[15]提出的基于重要趋势点的分段线性算法,即若一个待测点的特征值在局部区间内与区间端点特征值的比值超过某个阈值,则认定该点为重要点;廖俊等[16]根据序列的特征首先找出重要趋势转折点,即趋势变化明显的点,进而通过某种规则删除相对不重要的点;陈帅飞等[17]提出了一种根据序列中极值点和变化幅度比较大的点来得到关键点的分段线性算法;而肖辉等[18]提出的基于时态边缘算子的时间序列分段线性表示法,则是根据时间序列的特征设计出一种时态边缘算子,并最终得到时间序列的边缘点。这种自顶向下的算法尽管在一定程度上提高了分段精度,但用户参数不易确定,且对整体考虑不足。
针对上述问题,本文提出一种以时态边缘算子TEO(Temporal Edge Operator)为基础的自主分段线性表示方法APLR_TEO(Autonomous Piecewise Linear Representation based on Temporal Edge Operator),该方法不仅精度高,在参数的设定上较为简单,有良好的适应性和稳定性,且时间复杂度不高,时间序列测试数据集经过表示后的可视化效果也不错,能准确刻画出时间序列的主要趋势特征。首先根据边缘极值点的度量方法得到边缘极值点序列,再通过一种自主分段线性启发式规则得到最终的关键点序列。该方法对分段点数的划分更精确,从而使得压缩率的调节更为灵活。同时,也能更精准地反映时间序列曲线的总体特征,大幅度提高了分段效率,拟合效果也更好。
2 相关定义
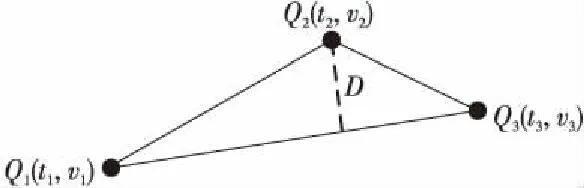
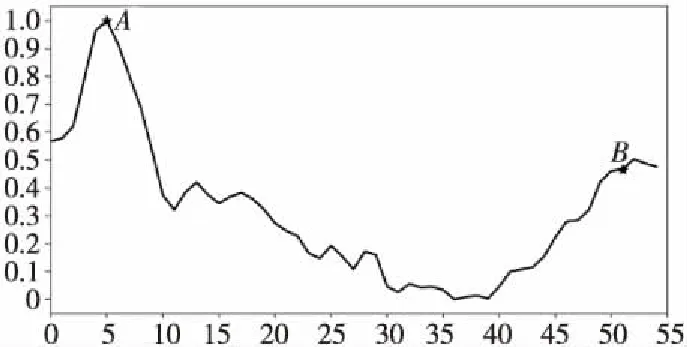
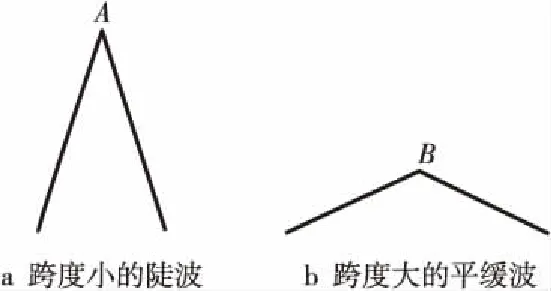
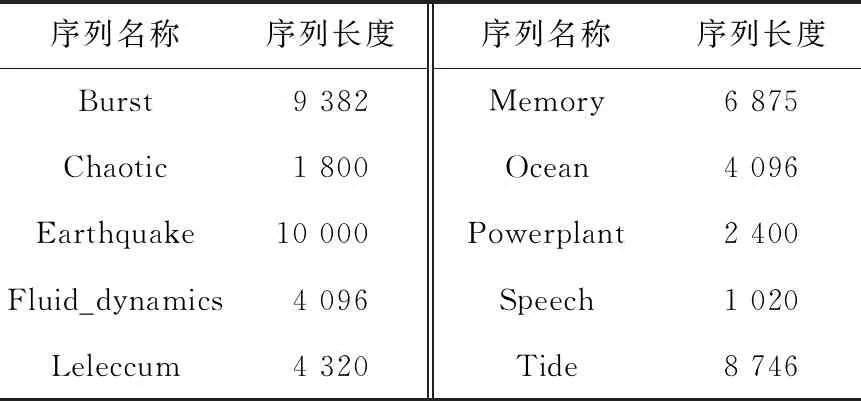
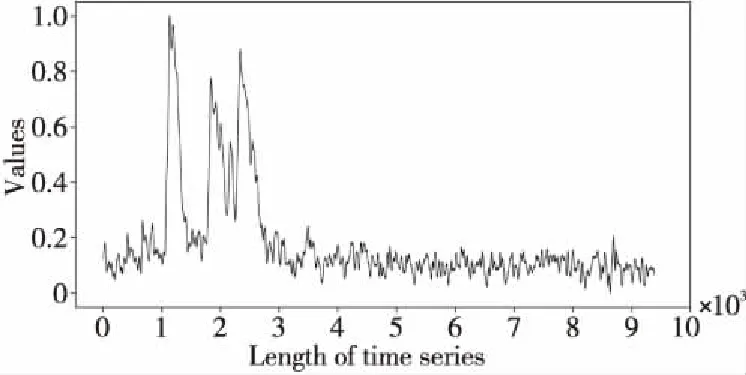
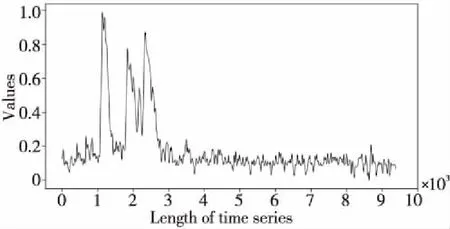
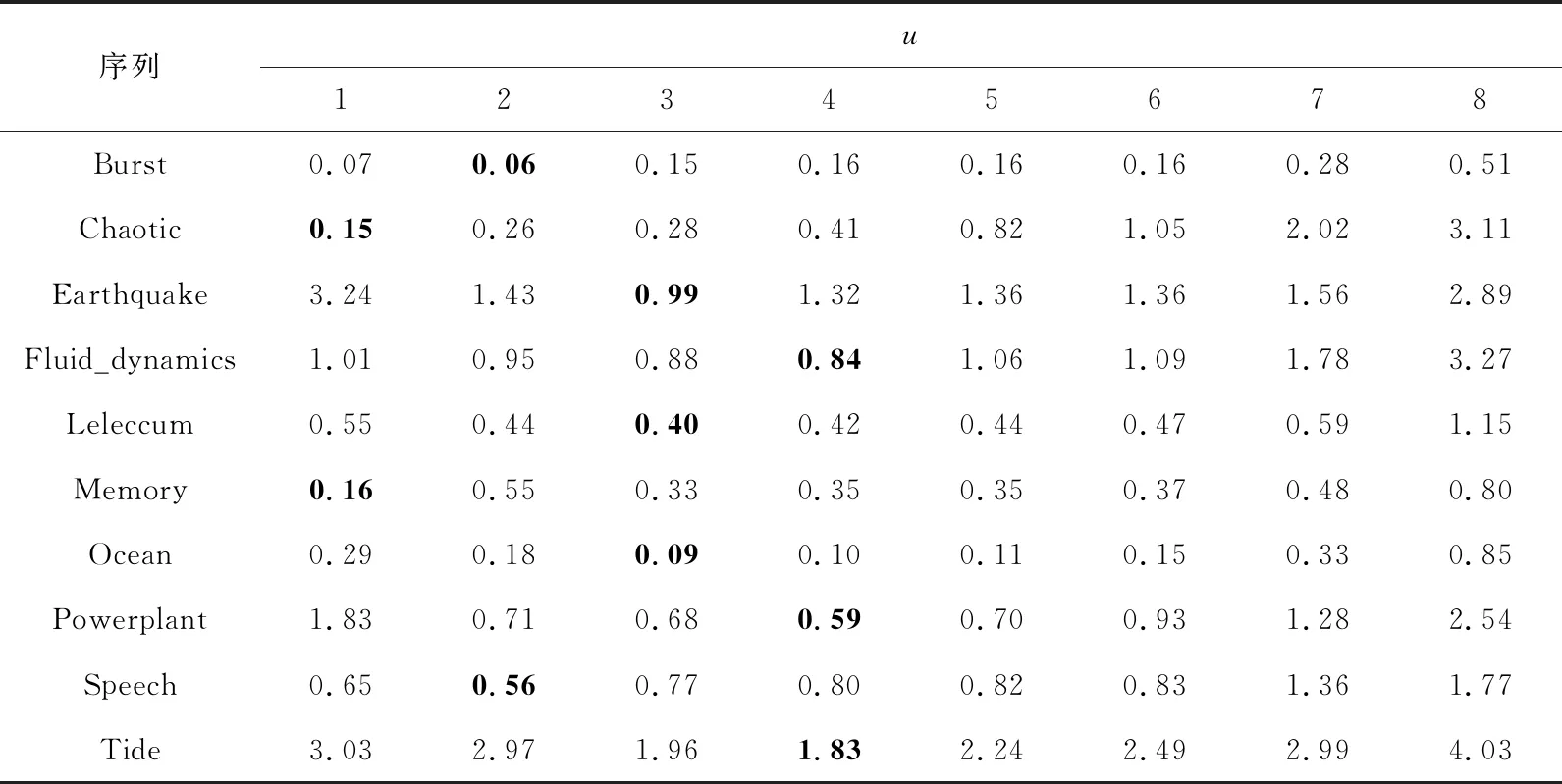
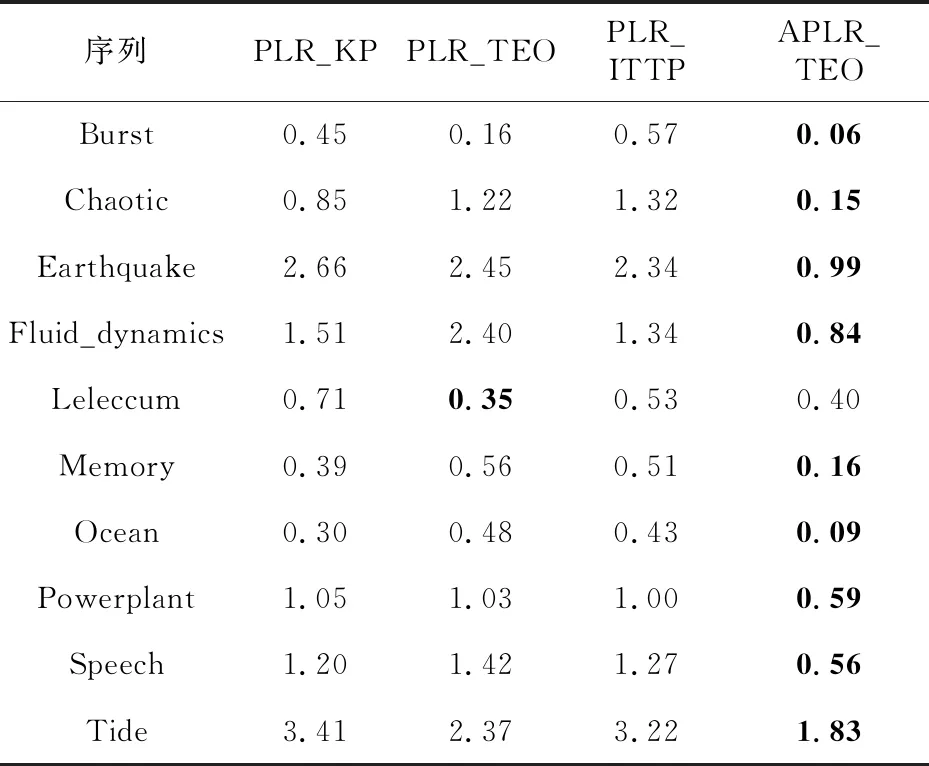
定义1(时间序列) 时间序列是一组由连续时间变量和对应的特征值组成的有序集合。从时间序列的角度来看,每个数据单元可以被抽象成一个二元组(t,v),t为时间变量,v为特征值变量。定义时间序列X={x1=(t1,v1),x2=(t2,v2),…,xn=(tn,vn)},满足ti X={x1,x2,…,xn} (1) 定义2(时间序列的分段线性表示) 设时间序列X={x1,x2,…,xn},分段点的集合记为X′={x′1,x′2,…,x′m},其中x′2=x1,x′m=xn,且m XL={f1(x′1,x′2),f2(x′2,x′3),…,fm-1(x′m-1,x′m)} (2) 其中,fm-1(x′m-1,x′m)表示在[x′m-1,x′m]上用于拟合时间序列的线性函数。 定义3(压缩率) 设原始时间序列X={x1,x2,…,xn},分段点的集合为X′={x′1,x′2,…,x′m},那么该时间序列的压缩率记为: (3) (4) 拟合误差是检验拟合时间序列和原始时间序列差异度的一个重要指标。在相同压缩率下,一个序列的拟合误差越大,那么拟合效果越差;反之,则拟合效果越好。这也是间接判断分段线性方法好坏的一个标准。 定义5(一维卷积) 与数字信号不同,本文采用的卷积计算是基于数字图像处理领域。众所周知,近几年图像处理成了热门的研究领域,二维卷积在该领域用处甚广,其原理是利用卷积核(卷积模板)在图像上滑动,将图像点上的像素灰度值与对应的卷积核上的数值相乘,然后将所有相乘后的值相加作为卷积核中间像素对应的图像上像素的灰度值,并最终滑动完所有图像卷积的过程,实质为矩阵与矩阵之间的卷积计算。而一维卷积原理与二维卷积相同,常用于序列模型和自然语言处理等领域,对于2个一维序列的卷积计算定义为: T*S=E (5) 其中,T∈Rn×1为时间序列,S∈Rn×1为与时间序列做卷积的边缘算子,而E∈Rn×1为本文所需的与时间序列等长的输出序列,*表示卷积运算符。 定义6(趋势转折距离) 设时间序列X={x1,x2,…,xn},在进行分段任务前,我们需要计算出当前点与其前后点之间的趋势偏转距离[19],如图1所示。 Figure 1 Trend deflection distance 图1中的Q1,Q2,Q3为在边缘极值点序列中的某邻域内的3个点,这3个点正好构成几何三角形,图1中垂直虚线段D的长度d就是趋势转折距离,定义为: (6) 其中,Q2(t2,v2)为待检测点。趋势转折距离d越大,这个点越重要。 APLR_TEO是一种自主分段线性表示方法。将时态边缘算子与原始时间序列进行卷积得到潜在边缘点序列,再通过过滤规则得到最终的关键点序列,并连接这些关键点之间的直线段序列来表示出原始时间序列。该方法主要分为2个部分:第1部分是基于时态边缘算子的边缘极值点度量方法的设计;第2部分是利用边缘极值点的自主分段线性方法,并得到关键点序列。 边缘算子[20]常用于检测图像的灰度级变化很快的点的集合(即图像的边缘),利用边缘邻近梯度值变化规律检测边缘。本文根据边缘算子的特征,设计出了符合时间序列特点的时态边缘算子,采用该算子来检测时序的边缘,并根据相应的关联规则从中提取出若干个边缘点,最后通过分段方法得到最终的分段序列点。在时间序列中,若一个序列点为边缘点,那么在其邻域内,位于该点左右两端的时间序列将呈现不同的变化趋势。在图2所示的时间序列中,序列点A左侧呈现上升趋势,右侧呈现下降趋势;而点B左侧呈现平缓趋势,右侧呈现上升趋势。因此,本文定义A,B为边缘点。这种左右邻域都有不同变化趋势的点,可称之为时间序列的边缘点[21,22]。 Figure 2 Edge points of a time series 本文将以时态边缘算子为基础,对分段线性算法进行改进,设计出一种基于时态边缘算子的自主分段线性表示方法APLR_TEO。 给定时间序列X={x1,x2,…,xn},定义时态边缘算子为: TEO(t,u)={w(i)×(xt+i-xi)|i= -u,…,-2,-1,0,1,2,…,u} (7) 该算子设计的基本思路是根据该点左右邻域相对该点变化幅度的影响来判断该点的重要程度,其中w(i)为计算边缘算子TEO的权重,定义为: w(i)=abs(i) (8) 即越靠近检测窗口中心的点权重越低,即只考虑该点邻域对当前点的变化幅度影响,u是检测窗口长度,由用户自己设定,实验表明,当u取1,2,3,4时,实验效果最好。可以针对数据集特征来选择合适的窗口进行边缘算子设计,该算子具有较强的适应性和灵活性。 根据定义5将TEO与时间序列做一维卷积计算: TEO(t,u)*X(t)=E(t) (9) 其中,TEO(t,u)是根据在线卷积计算时间序列点得到的相应的时态边缘算子,X(t)为当前卷积的序列点,E(t)为输出的边缘强度序列。 由于时序关联性强的特点,相邻点的边缘幅度相近,若用这些边缘点进行线性分段,无法准确刻画时序的主要特征。下面将给出一种边缘点的度量方法。 经过TEO卷积计算得到的对应的边缘强度序列记为E={e1,e2,…,en}。若X={x1,x2,…,xn}满足以下条件之一: (1)ei>ei-1且ei≥ei+1,或ei≥ei-1且ei>ei+1,其中1 (2)ei 点ei即为相应的边缘强度极值序列点,由此可找出与之对应的时间序列边缘极值点xi,并将这些边缘极值点放入边缘极值点序列集合Q={q1,q2,…,qm}中,最终,就可以得到边缘极值点序列Q={q1,q2,…,qm},其中m 设时间序列X={x1,x2,…,xn},其输出的关键点序列为{xi1,xi2,…,xik},其中1≤i1≤i2<… (10) 其中,L(xik-1,xik)表示在区间[ik-1,ik]上连接相邻关键点的线性函数,式(10)也可简化为L′={L(xi1,xi2),L(xi2,xi3),…,L(xik-1,xik)}。 由于时间序列具有不稳定性和相关联性的特点,本文提出了APLR _TEO方法,通过提取边缘极值点并进一步经过自主分段线性表示的关联规则来选择合适的关键点表示时间序列的整体特征。 自主分段线性方法实现过程:设时间序列为X={x1,x2,…,xn},通过3.2节的度量方法得到边缘极值点序列为Q={q1,q2,…,qm}。再从边缘极值点序列中筛选出关键点序列Kpts,默认将首尾点q1和qm加入到关键点序列,在计算趋势转折距离的过程中,默认将最后一个点qm作为图1的Q3,将第1个关键点q1初始化为图1的Q1。初始化累积分段转折距离sum_d=0和分段内的最大转折距离max_d=0,并根据压缩率设定累积分段阈值ε。遍历边缘极值点序列,得到序列中每个点的趋势转折距离dk,同时计算累积转折距离sum_d=d1+d2+…+dk,其中dk是从q2开始计算的趋势转折距离,k≤m-2。判断dk是否大于最大转折距离max_d,若max_d 基于边缘极值点度量的自主分段线性方法伪代码如下所示: 输入:时间序列X={x1,x2,…,xn},参数u,ε。 输出:关键点序列Kpts。 步骤1初始化时间序列X; 步骤2构造边缘极值点序列Q,默认将X中的首尾点加入到Q中: fori=1 ton 计算序列X与TEO卷积后的边缘强度序列Eepts: Eepts←X(i)*TEO(i,u);E_index←i; endfor forj=1 tom 根据边缘极值点的关联规则找出与E对应的边缘极值点序列: Q←X(E_index[j]); endfor returnQ 步骤3构造关键点序列Kpts: fori=1 tom 计算Q中每个点的分段趋势转折距离di; sum_d+=di; max_d←di; max_index←i;//max_index为索引列表 if(sum_d>ε) iIndex←max_d.index(max(max_d)); Kpts← (max_index[iIndex],Eepts[max_index[iIndex]]); endif endfor returnKpts (1)APLR_TEO方法只需设定2个参数,分别是边缘算子卷积窗口大小u和累积分段阈值ε。其中,参数u将通过第4节实验说明其容易确定,在针对不同数据集时,灵活性和适应性很强;而参数ε则是根据压缩率大小上下浮动的,其变化范围小,也不难确定。本文方法与文献[17]中所提及的PLR_KP(Piecewise Linear Representation based on Key Points)方法的3个阈值参数C,P,R相比,需要设定的参数更少,参数的大小更容易确定。 (2)APLR_TEO方法综合考虑了拟合误差大小与时间跨度问题。PLR_ITTP(Piecewise Linear Representation based on Important Trend Transition Points)方法[16]对于分段的约束条件只是针对前一重要点和后一趋势转折点形成的线段距离大则拥有优先分段权这一局部约束,忽略了序列的全局特征,则会造成图3a 这种时间跨度小而波形陡的情况,即点A的趋势转折距离更大。出于降低拟合误差考虑,这种分段方式往往会造成更大的拟合误差。相比较而言,图3b中B点的趋势转折距离小,时间跨度大,最终的拟合误差也较小,更能准确反映波形趋势特征。利用这一特征,APLR_TEO解决了PLR_ITTP方法未考虑时间跨度这一全局性的问题,在计算趋势转折距离的同时,累加分段距离,并根据累积分段阈值来判断是否结束该局部分段,从而达到精确地整体分段,降低整个序列拟合误差的目的。 Figure 3 Time span of trend turning points (3)APLR_TEO方法对时间序列进行了2次扫描选取关键点,其时间复杂度为O(n),n是时间序列长度。总体来说,计算成本不高比较容易实现。 为了验证APLR_TEO方法的有效性,本文在一系列标准时间序列数据集上进行时间序列的拟合误差度量,分别比较在相同压缩率和不同压缩率下几种分段线性方法的拟合效果。 实验数据集采用Keogh等[13]提供的公开数据集KData。KData数据集包括了来自不同应用领域的数据集,被广大时间序列研究者们采用。本文从KData中选取了研究者们常用的10个序列进行方法的对比评估,选取的序列如表1所示。 Table 1 Description of KData dataset 为了验证APLR_TEO的性能,将本文方法与廖俊等[16]提出的基于极值点的分段线性方法PLR_ITTP、陈帅飞等[17]提出的一种基于关键点的时间序列线性表示方法PLR_KP和肖辉等[18]提出的基于时态边缘算子的时间序列分段线性表示方法PLR_TEO这3种不同的分段线性方法进行对比。 本文提出基于时态边缘算子的自主分段表示方法APLR_TEO,将时态边缘算子与时间序列做卷积得到边缘极值点,并根据一种自主的线性分段方法得到最终的关键点序列。方法需要输入2个参数,参数u表示进行卷积的时态边缘算子窗口大小,参数ε为累积分段阈值。由于时间序列来自不同领域,彼此的特征值取值范围有一定差距,为了便于对比实验,在采用线性分段方法之前首先对时间序列做规范化处理,将序列特征值规范化到[0,1],其规范化公式如式(11)所示: (11) 实验运行在2.5 GHz CPU,8 GB内存Windows系统的Python 3.5.1环境下,在运行前样本都已按规范化处理。本文选取了KData中的10个序列进行拟合误差对比实验。 以Burst序列为例,该原始序列长度为9 382,原始序列如图4所示 ,在压缩率为80%时采用APLR_TEO方法表示得到的拟合序列如图5所示,可以明显看出该方法能很好地刻画出序列的总体趋势和特征。 Figure 4 Original Burst sequence (9 382 sections) 接下来,为确定时态边缘算子窗口大小,在KData数据集上进行APLR_TEO方法的性能评估。表2是在压缩率为80%,u∈{1≤u≤8|u∈N}的条件下,u取不同值时,APLR_TEO的拟合误差,其中加粗数据即为拟合误差最小值。从表2可以看出,在测试的10条序列中,有2条序列在u=1时拟合误差最小;有2条序列在u=2时拟合误差最小;有3条序列在u=3时取得最小拟合误差;有3条序列在u=4时取得最小拟合误差。当u≥5时,拟合误差值呈上升趋势,且u取值越大,拟合误差的增长幅度也越大。因此,在实际的运算过程中取1≤u≤4,在APLR_TEO方法中增加一个记录环节,即用一个for(u=1;u<5;u++)循环,来记录当u取何值使得方法的拟合误差最小。 Figure 5 Fitting Burst sequence (1 876 sections) 在统一压缩率为80%的条件下,比较PLR_ITTP、PLR_KP、PLR_TEO、APLR_TEO这4个方法在10个通用序列上的拟合误差,实验结果如表3所示。从表3中可以看出,当压缩率为80%时,APLR_TEO方法在其中的9个序列上的拟合误差都是最小,方法的整体表现优异。这10个序列都是维数在1 000维以上的高维序列,也从侧面反映了APLR_TEO方法在高维数据集上所表现出的良好性能。如在Earthquake超高维序列上,APLR_TEO与其他3种方法的拟合误差对比的差值更明显,即APLR_TEO方法在高维数据集上的适用性更好。同时,这10个序列分别来自不同领域,本文算法在不同领域时间序列上都表现得十分出色,可见方法本身的适应性也很强。 Table 2 Fitting error of APLR_TEO representation Table 3 Comparison of fitting errors when compression rate is 80% 以Ocean数据集为例,比较PLR_ITTP、PLR_KP、PLR_TEO、APLR_TEO这4种方法在不同压缩率下的拟合误差,结果如图6所示。随着压缩率的增大,即分段数减少,拟合误差随之增加。而压缩率越高,拟合误差的上升幅度越大。在不同压缩率下,APLR_TEO方法的拟合误差明显小于PLR_ITTP、PLR_KP和PLR_TEO这3种方法的。 Figure 6 Comparison of fitting errors under different compression rates 本文将时态边缘算子(TEO)引入时间序列的分段线性中,提出一种基于时态边缘算子的时间序列自主线性分段表示方法。该方法利用时态边缘算子与时间序列做卷积,得到边缘极值点;再根据邻域内的趋势转折距离来得到关键点。该分段算法很好地利用了邻域内变化明显的点,通过累计趋势转折距离的判断机制实现了自主线性分段。 在一系列KData数据集上进行了拟合效果评估,实验结果表明,本文方法有较强的适应性和稳定性,且对噪声不敏感,能有效地压缩时间序列。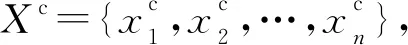
3 时态边缘算子的自主分段方法
3.1 时序边缘算子和边缘点
3.2 边缘极值点度量
3.3 自主分段线性方法
3.4 方法分析
4 实验与分析
4.1 数据集描述
4.2 实验方法
4.3 实验结果与分析

5 结束语
