基于改进型柯西变异灰狼优化算法训练的多层感知器*
2021-06-25王栎桥张达敏王依柔
王栎桥,张达敏,樊 英,徐 航,王依柔
(贵州大学大数据与信息工程学院,贵州 贵阳 550025)
1 引言
神经网络NN(Neural Network)是智能计算领域最伟大的发明之一,它模仿了人类大脑的神经元并主要用于解决分类问题和进行数据预测。1943年,神经网络的概念被首次提出。从此,神经网络得到迅速发展,不同类型的神经网络相继被提出,多层感知器神经网络MLP NN(MultiLayer Perceptron NN)是该领域最著名的分类器之一,已经有广泛的研究应用。一般来说MLP分为2大类:有监督的和无监督的[1]。训练器负责训练MLP。多年来,反向传播技术及其变体[2]在MLP神经网络训练中发挥着重要作用。然而,基于梯度下降及其变种的方法存在收敛速度慢、易陷入局部极小值、对初始参数[3]的依赖性强等缺点。因此,群智能算法是高维问题中最适用的训练器之一,因为它具有随机性,可以有效地避免局部最优。另一方面,单解算法和多解算法是随机方法的2大类。在高维问题[4]中,多解算法相比较单解算法可以防止训练器陷入局部最优。有大量著名的多解群智能算法被用来训练神经网络[5 - 11],尽管各种群智能算法之间存在差异,但是,群智能算法都是将解空间内的寻优过程划分为探索和开发2个阶段。在很多情况下,由于群智能算法的随机性,开发和搜索2个阶段之间没有明确的界限[12],2个阶段之间的不平衡使得算法陷入局部最优[13]。这些基于群智能的随机优化算法在很大程度上降低了陷入局部最优的概率,但它们在收敛速度和收敛精度方面仍然不尽人意[14]。
灰狼优化GWO(Grey Wolf Optimizer)算法是以最优个体(α狼)引导的算法,其带领狼群进行局部探索。在训练MLP的过程中GWO算法使用的线性递减收敛函数导致全局探索能力不足而不能得到最优解。针对这一缺点,为了平衡算法的局部开发和全局探索能力[15],本文使用余弦收敛函数代替线性递减收敛函数;同时,在训练MLP模型时,其解空间的极值可能分布在临近的位置,本文引入柯西变异算子有效提升算法的局部开发能力和抵抗陷入局部最优的能力。为了提升算法的鲁棒性,本文尝试将柯西变异算子和余弦收敛因子引入到GWO中,对其位置更新方程进行改进,并将改进型柯西变异灰狼优化IGWO(Improved Cauchy variant Grey Wolf Optimizer)算法作为MLP的学习算法对其进行训练。数值实验结果表明,IGWO算法作为MLP的训练器时能明显提升分类准确率,并有较好的鲁棒性。相对于其他常见的智能算法其训练时长也有所缩短。
2 灰狼优化算法
灰狼优化算法是通过对狼群的种群层次结构、捕食过程、围捕及攻击行为进行分析研究,建立的过程简单、参数设置较少的快速智能算法模型[16]。灰狼优化算法通过对种群中的个体的适应度值降序排列,将排列第1的定义为α狼,即头狼,将领导狼群的动作。第2的定义为β狼,第3的定义为δ狼,它们将协助α狼,剩余的为ω狼。所以,假设在M维的空间中,共计N匹狼组成的狼群,将其所在的位置记为X,第i匹狼所在的位置表示为Xi=(xi1,xi2,…,xim,…,xiM)。
灰狼优化算法模拟了灰狼的包围策略,提出了模拟灰狼包围行为的搜索方程。其行动方式可以描述为:
A=2ar1-a
(1)
C=2r2
(2)
a=2-t/tmax
(3)
Di=|C·Xp(t)-X(t)|
(4)
Xi(t+1)=Xp(t)-ADi
(5)
式(1)~式(5)描述的为围猎过程,其中A和C是系数向量;r1和r2是[0,1]的随机向量;tmax是最大迭代次数;a为从2线性递减至0的收敛因子。Xp(t)表示猎物的位置向量;Xi是狼群中i狼的位置。
狼群狩猎过程可以被描述为:
(6)
(7)
(8)
式(6) ~式(8)中,Xi(t)代表狼群中各ω狼的当前位置,Xi(t+1)为狩猎行为后的位置。Xα(t)、Xβ(t)和Xδ(t)分别代表当前时刻α狼、β狼和δ狼的位置,C1、C2和C3是(0,1)的随机数,A1、A2和A3是系数向量。
3 改进型柯西变异灰狼优化(IGWO)算法
3.1 余弦收敛函数
收敛因子a影响狼的全局搜索能力和局部搜索能力。不同的a(t)的减速率对应不同的算法搜索性能。在灰狼优化算法中收敛因子a线性递减,随着迭代次数的增加,收敛速度由慢变快,这能平衡算法全局探索和局部开发[17]。在训练MLP时,本文引用一种基于余弦的收敛因子公式,如式(9)所示。
a(t)=2×cos((t/tmax)*(π/2))
(9)
其中,a(t)是第t代收敛因子,tmax是最大迭代次数。
使用余弦收敛因子代替常规线性收敛因子,能够保证有一个大的收敛因子,有利于全局探索;相反,一个小的收敛因子则有利于局部开发。使用余弦收敛因子能平衡GWO算法全局探索和局部开发能力。
3.2 引入柯西变异算子
灰狼优化算法容易早熟,陷入局部最优,因此本文在算法中引入了柯西变异算子。根据柯西分布的特点,柯西变异因子是对潜在最优灰狼个体的局部区域进行搜索,在一定的潜在最优解范围内产生随机扰动,增强了算法的局部搜索能力,并测试了其最优位置[18]。柯西异变基于柯西概率密度函数,如式(10)所示:
(10)
其中,x0是位置参数,γ是一个大于0的随机变量,x是一个实数。本文中取x0=0,γ=1,其为标准柯西分布。通过分析其概率密度函数,可知其没有特定的均值和方差,但众数和中值都等于位置参数,即x0。其分布函数如式(11)所示:
(11)
柯西分布和正态分布相比较,柯西分布的整体分布更加均匀,对称轴的最大值相对于高斯分布较为平缓,而2边曲线所对应的拖尾概率较大。这样的分布特点,使柯西分布具有较大的散布特性。本文将会加入的扰动公式如式(12)和式(13)所示:
Xibset(t)=Xi(t)+Xi(t)*G(x)
(12)

(13)
其中,f(Xi(t))表示i狼在第t次迭代时的适应度值。通过局部扰动,引导算法跳出局部最优。
3.3 自适应位置更新公式
本文引用了一种自适应调整策略,将适应度值的倒数作为更新公式的权重系数[19],这样增加了3匹头狼的位置优势,使适应度值高于种群平均适应度值的狼的位置更新趋向最优解,提高算法的收敛速度。所以,用式(14)代替式(8)作为狼群位置更新公式。
(14)
其中,f(Xi(t))代表i狼在第t代时的适应度值,fα、fβ和fδ分别表示第t代时α、β和δ3匹头狼的适应度值。favg代表第t代种群中所有狼的适应度平均值。
3.4 IGWO的算法实现
综上所述,本文提出的IGWO算法实现过程如算法1所示。
算法1基于改进型柯西变异的灰狼优化算法IGWO
Step1算法参数初始化,灰狼种群规模N;最大迭代次数tmax;变量空间维度M;空间变量的上界和下界ub和lb。
Step2初始化种群。
Step3令迭代次数t=1。
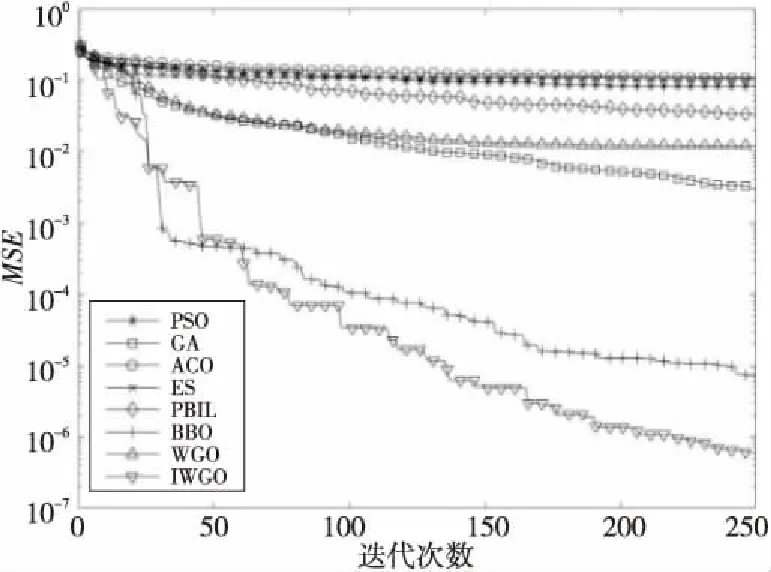
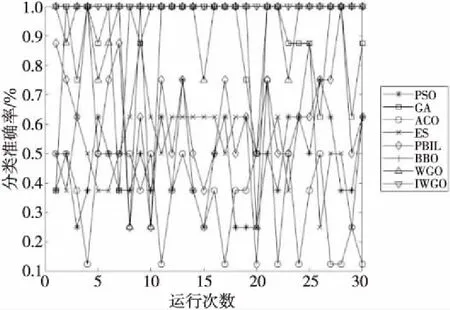
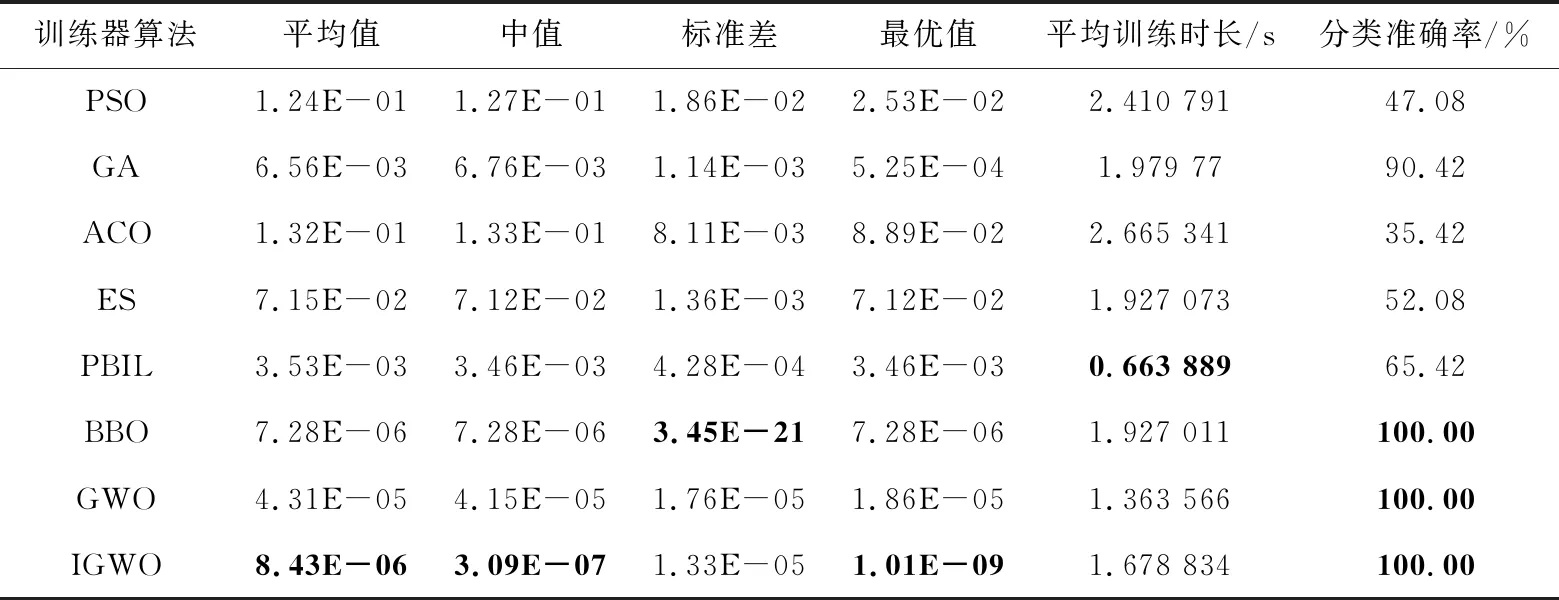
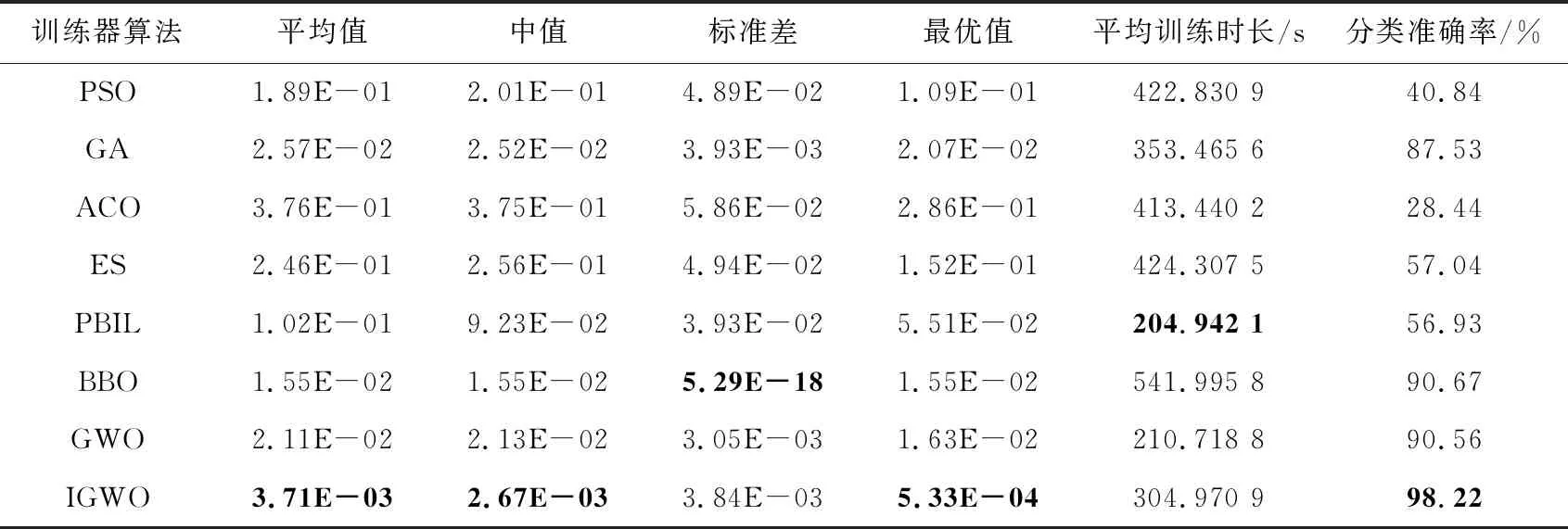
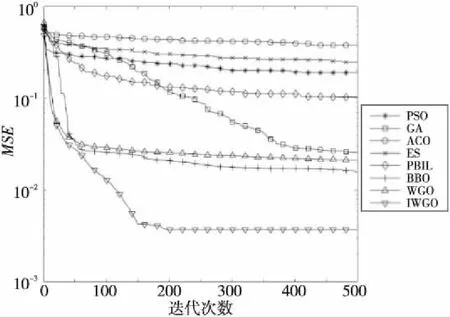
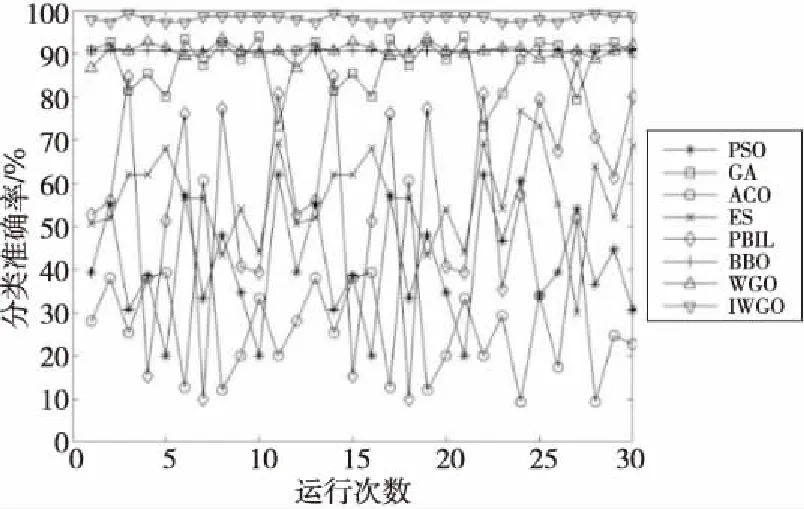
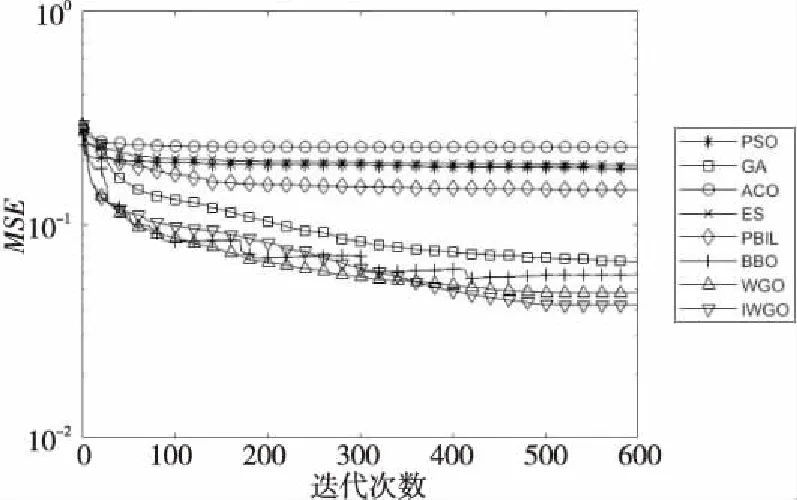
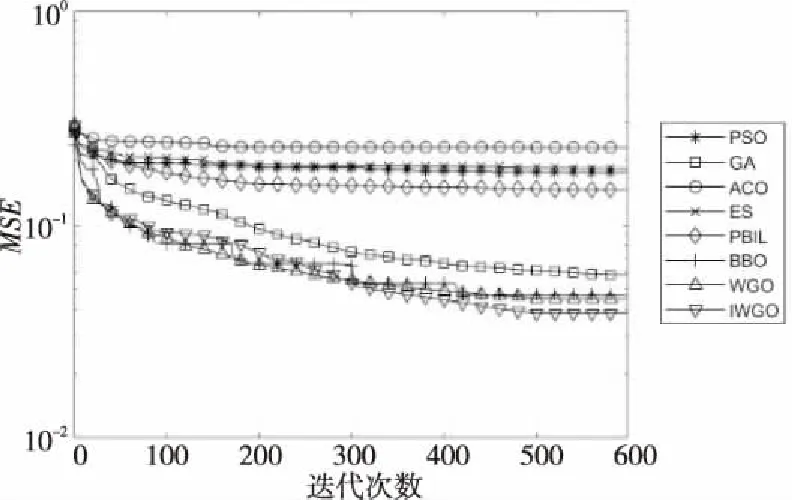
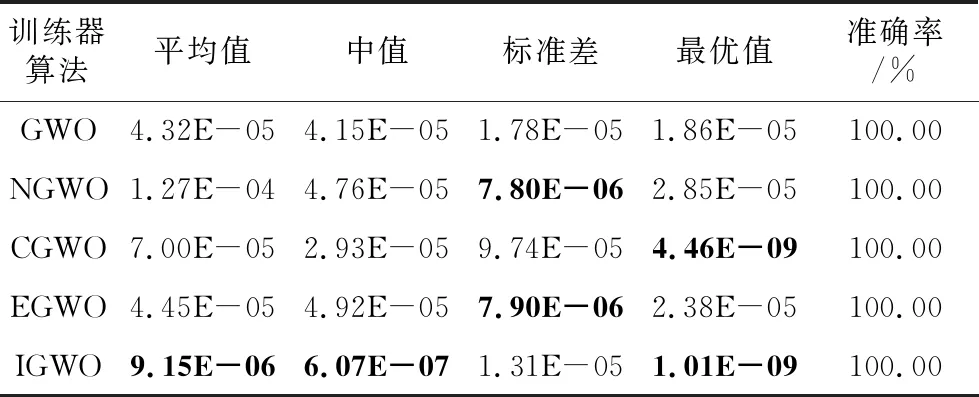
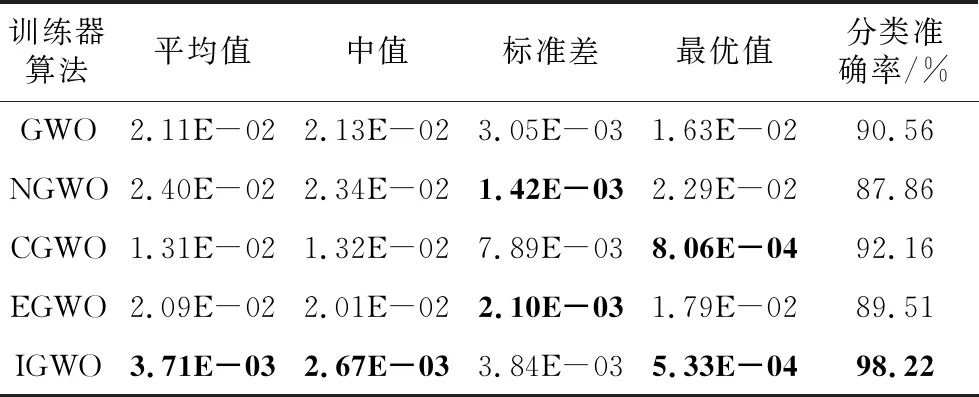
Step4当t Step5计算狼群中适应度值{f(Xi),i=1,2,…,N}, 其中适应度值最高的个体为α狼,β狼与δ狼。 Step6利用式(9)更新收敛因子a(t)。 Step7利用式(6),式(7)和式(14)更新当前迭代次数中各狼的位置。 Step8计算当前迭代次数中各狼的适应度值{f(Xi(t)),i=1,2,…,N}。 Step9找出位置更新后的α狼,β狼与δ狼。 Step10根据式(14)更新狼群,令t=t+1。 Step11若达到最大迭代次数,则结束;否则跳转Step 4。 利用IGWO算法训练多层感知器的流程如图1所示。 Figure 1 MLP trained by IGWO algorithm 对于多层感知器MLP,由于数据空间样本多为高维空间,多模式,同时也有可能存在数据被噪声干扰,有冗余数据和数据丢失的情况。训练MLP的主要目的是更新权重和偏置,这是一个极具挑战性的优化问题。本文使用智能优化算法优化MLP的训练[20],将各个节点的权重和偏置编码为输入向量V,如式(15)所示: V={W,θ}={w1,1,w1,2,…,wn,n,θ1,θ2,…,θn} (15) 其中,wi,j表示为节点i和节点j相连的权重。θj表示节点j的偏置,n为节点总数。为了检验算法训练MLP的效果,定义以下变量: 定义1(均方差MSE(Mean Square Error)) 通过将样本的数据输入MLP的输入层,将MLP的输出数据与目标结果比较,若输出数据与目标结果越接近,则训练效果越好,反之训练效果越差。MSE定义如式(16)所示: (16) 定义2(训练器分类准确率CA(Classification Accuracies)) 这是衡量算法分类器性能的重要指标,在不同的问题中,也可能被称为“精度”或“准确率”。其定义如式(17)所示: (17) 其中,Si代表着样本中待分类的假设集合S中第i个属性的个数。Ti表示数据集中正确分类的样本个数。 (1)实验问题设置。 为了测试本文IGWO算法训练MLP的性能,选择了3个分类问题进行测试,分别为:3位奇偶校验问题(XOR)、鸢尾花分类问题(Iris)和心脏病UCI问题HD UCI(Heart Disease UCI)。对于多层感知器的网络结构设置,隐藏层节点数为2k+1,其中k为数据集的特征个数。对于XOR问题、Iris问题,多层感知器的结构为3-7-1、4-9-3;对于HD问题,使用22-45-1和22-16-1结构的MLP作为训练对象。XOR问题设置的目的是讨论简单结构MLP中智能算法作为训练器的性能;Iris问题设置的目的是测试对于输出层有多个节点的情况智能算法的性能;HD问题设置的目的是当面对节点数量较大的MLP时测试智能算法训练器的性能表现。因此,对于4种不同结构的多层感知器智能算法种群规模分别设置为50,200,200,200。最大迭代次数分别为250,500,650,650。 (2)对比算法参数设置。 同时作为对比,本文选择了PSO (Particle Swarm Optimization)[5]、GA (Genetic Algorithm)[6,7]、ACO (Ant Colony Optimization)[8,9]、PBIL (Population-Based Incremental Learning)[10]、ES (Evolutionary Strategy)、BBO (Biogeography-Based Optimization)[11]和GWO[16]算法作为MLP的训练器对3个不同的研究问题进行实验。根据大量参考文献选取经验值,在训练中各个算法的参数设置如下: 对于PSO,c1和c2的值设置为2,r1和r2为0~1的随机数,ω从0.9线性递减到0.4,初始粒子速度在0~1随机生成。 对于BBO算法,最大迁入率为1,最大迁出率为1,变异概率为0.005,迁移概率取值为0~1,步长为2。 对于ACO算法,信息素值为10-6,信息素常数为20,探索常数为1,全局信息素衰减率为0.9,局部信息素衰减率为0.5,信息素敏感度α=1,信息素敏感度β=5。 对于GA算法,单点交叉,交叉概率为1,初始变异概率为0.01。 对于PBIL算法,学习率r0=0.05,变异概率为0.5,变异速率为0.1,最大变异率V0=0.4,学习速率调整时系统熵的阈值ε=10-6。 对于ES算法,每次新一代产生后代的数量为10,保留至下一代的精英数量为2,突变成功概率为0.005,进化步长σ=1。 3位奇偶校验问题是一个著名的非线性标准测试问题。本文把3位奇偶校验问题的MLP结构设置为3-7-1,即3个输入,7个隐藏层节点和1个输出层节点,并分别对8种算法进行30次独立实验,选取的统计参数有:平均值、中值、标准差和最好值,统计结果如表1所示,平均收敛趋势和分类准确率如图2和图3所示。 由图2可以看出,ACO、ES、PSO、PBIL和GA算法的收敛速度远不及其余3个算法的。BBO和GWO算法的收敛精度逊色于IGWO算法。但是,通过表2可以看出,在达到相同分类准确率的情况下,IGWO算法的平均训练时长比BBO算法的短。图3是各个智能算法作为MLP的训练器,进行30次独立运算的MES的收敛曲线。通过表2可知,IGWO在平均值、中值和最优值上都是最佳的。 虽然在标准差上能看出BBO算法具有较好的鲁棒性,但是收敛精度不如IGWO的,由表1可知各个算法实际所用时长,其中PBIL算法所用时间最短,但是其分类准确率只有65.42%。同时具有较好鲁棒性的BBO算法训练所消耗的时间也是最长的。IGWO算法在更短时间内得到了更好的收敛精度,分类准确率达到100%。与GWO算法相比,IGWO的寻优性能得到了很大的提高,达到了性能改善的目的。 Figure 2 MSE convergence curve of each algorithm for XOR problem Figure 3 Classification accuracy of each algorithm for XOR problem Table 1 MSE and classification accuracy of intelligent algorithms for XOR problem Table 2 MSE and classification accuracy of intelligent algorithms running independently 30 times for Iris problem 鸢尾花问题数据集有150个训练样本,共4个基本特征。本文选择MLP的结构为4-9-3来对该问题进行分类。其统计结果如表2所示,平均收敛趋势和分类准确率如图4和图5所示。 Figure 4 MSE convergence curve of each algorithm for Iris problem Figure 5 Classification accuracy of each algorithm for Iris problem 由表2可知,对于Iris问题,从8种算法独立运行30次的结果来看,IGWO的平均值、中值和最优值都比其余7种算法的好,这表明了在处理多输出节点的MLP问题时,IGWO算法的收敛精度都高于其他7个算法的,同时在MLP的测试样本分类准确率上IGWO也要高于其他算法。同时,IGWO与GWO具有相近的标准差,表明IGWO算法继承了GWO算法的强鲁棒性,且比ACO、ES、PSO、PBIL和GA算法的鲁棒性要好。虽然IGWO的标准差不如GWO和BBO的,排名第3。从训练时长看,BBO算法消耗的时间远远多于IGWO算法的。由图4和图5 8种算法对Iris分类问题的分类收敛曲线可知,ACO、ES、PSO、PBIL和GA算法的收敛速度和收敛精度较差,BBO和GWO算法的收敛精度相近,IGWO收敛精度最高。而BBO的稳定性好于GWO和IGWO的。从图5中可以看出,虽然IGWO的鲁棒性与GWO相近,不如BBO算法,但IGWO拥有更快的收敛速度,IGWO的收敛精度和鲁棒性远高于ACO、ES、PSO、PBIL和GA算法的。这充分验证了IGWO算法的强鲁棒性、分类可靠性和高效性。 心脏病问题HD UCI来自克利夫兰数据库,是迄今为止ML(Machine Learning)研究人员使用的唯一数据库。这个数据库包含76个属性。使用2种不同结构的MLP作为训练对象,22-16-1结构MLP是一种收敛形的结构,其隐藏层个数为输入层与输出层节点数总和的2/3。22-45-1结构MLP选择的是常规的隐藏层节点数,其选取节点数为2k+1,k为数据集的特征个数。 使用8种不同的智能算法训练结构为22-16-1的MLP处理HD分类问题,其统计结果如表3所示,平均收敛趋势和分类准确率如图6和图7所示;训练结构为22-45-1的MLP处理HD分类问题的统计结果如表4所示,平均收敛趋势和分类准确率如图8和图9所示所示。 由表3和表4可以看出,在HD分类问题中,22-16-1结构MLP的MSE和分类准确率不如22-45-1结构的,虽然其较少的节点数降低了智能算法探索的解空间维度,使算法的训练时长缩短了,但是其训练后的MSE和分类准确率不如22-45-1结构的MLP。22-16-1结构的MLP不能完全区别特征,导致训练后的MSE和分类准确率不如22-45-1结构的MLP。 Figure 6 MSE convergence curve of MLP with 22-16-1 structure training by each algorithm for HD problem Figure 7 Classification accuracy of MLP with 22-16-1 structure training by each algorithm for HD problem Figure 8 MSE convergence curve of MLP with 22-45-1 structure training by each algorithm for HD problem Figure 9 Classification accuracy of MLP with 22-45-1 structure training by each algorithm for HD problem Table 3 MSE and classification accuracy of MLP with 22-16-1 structure training by each algorithm for HD problem Table 4 MSE and classification accuracy of MLP with 22-45-1 structure training by each algorithm for HD problem 从8种算法训练的22-16-1结构MLP处理HD问题独立运行30次的统计结果来看,IGWO的平均值、中值和最优值都比其余7种算法的好,这些都表明了在处理大量关联节点的MLP问题时IGWO算法的收敛精度高于其他7个算法的,同时在MLP的测试样本分类准确率上IGWO也要高于其他算法的。BBO算法在标准差上的表现体现出其鲁棒性良好,但是由表4可知,在训练耗时上其表现不如GWO和IGWO算法的,在分类准确率上其不如GWO的。IGWO的标准差低于GWO的,其稳定性更高。 由图6~图9中8种算法训练22-16-1结构MLP处理HD分类问题的MSE收敛曲线可知,ACO算法的收敛速度和收敛精度最差,然后依次为GA、PSO、ES和PBIL算法。同时BBO算法和GWO算法的收敛精度不如IGWO算法的。 以上统计结果表明,IGWO算法训练22-45-1结构的MLP处理HD问题性能较好。IGWO算法的寻优性能和训练速度得到了很大的提高,达到了性能改善的目的。 表5和表6分别展示了GWO算法及其各个改进算法训练多层感知器,处理XOR分类问题和Iris分类问题独立运行30次后的MSE、分类准确率的平均值。表5中,GWO算法及其改进算法训练MLP处理XOR问题的最大迭代次数为200次,选择200作为最大迭代次数是因为此时分类准确率已经达到100%,前文中最大迭代次数为250次是为了对比其他智能算法。表7展示了GWO算法及其改进算法训练22-16-1结构MLP处理HD分类问题独立运行30次后的MSE和分类准确率的平均值。表8展示了GWO算法及其改进算法训练22-45-1结构MLP处理HD分类问题独立运行30次后的MSE和分类准确率的平均值。 其中,NGWO是将GWO算法的线性收敛因子替换为余弦收敛因子,如式(9)所示。CGWO是在GWO算法中增加了柯西变异算子式(13)。EGWO是将GWO算法的位置更新公式替换为式(14)。IGWO是将余弦收敛因子、柯西变异算子和位置更新公式替换都加入GWO算法中。 Table 5 MSE and classification accuracy of GWO and its improved algorithms running independently 30 times for XOR problem Table 6 MSE and classification accuracy of GWO and its improved algorithms running independently 30 times for Iris problem Table 7 MSE and classification accuracy of MLPwith 22-16-1 structure trained by GWO and its improved algorithms for HD problem Table 8 MSE and classification accuracy of MLP with 22-45-1 structure trained by GWO and its improved algorithms for HD problem 通过表5可知,GWO及其改进算法训练多层感知器处理XOR分类问题的分类准确率已经达到100%。从MSE的角度看,加入柯西变异算子可以提升局部探索能力,得到的最优值更小;标准差也反映了单独加入柯西变异算子会使算法鲁棒性降低;为了保证鲁棒性,同时加入余弦收敛因子和位置更新公式(式(14)),可以从多次训练的标准差看出使用位置更新公式(式(14))和余弦收敛因子可以提升鲁棒性。通过表6可知,GWO及其改进算法训练多层感知器处理Iris分类问题的准确率均在90%以上。从MSE的角度看,Iris分类问题相较于XOR问题使用的MLP的节点数较多,对于训练算法而言其解空间维度更高。可以看出解空间维度提升以后,柯西变异算子提升局部探索的能力依然有效,能找到更优的最优值,但是通过标准差可以看出,加入柯西变异算子对鲁棒性存在影响。从标准差看,加入余弦收敛因子和使用位置更新公式(式(14))可以提升算法鲁棒性。改进后的IGWO算法训练多层感知器处理Iris分类问题能在保证鲁棒性的同时提升准确率和降低MSE。通过表7和表8可知,GWO及其改进算法训练不同结构的训练多层感知器处理HD分类问题时,22-16-1结构MLP在同样训练后的表现不如22-45-1结构MLP,是因为收敛形的MLP结构不能完全区分特征。为了处理HD分类问题,2种MLP的节点数量有大幅提升,对于训练算法而言其解空间维度更高。从MSE的最优值可以看出,处理高维解空间时,柯西变异算子提升局部探索的能力依然有效。从30次独立运算的标准差可以看出,使用余弦收敛因子和更新公式(式(14))处理高维解空间能提升算法鲁棒性。IGWO算法训练大量节点的多层感知器处理HD分类问题时能在保证鲁棒性的同时提升分类准确率和降低MSE。 使用启发式算法作为MLP的训练器是一个可行的方向,本文算法在GWO算法基础上加入柯西变异算子提升算法跳出局部最优的能力,加入余弦收敛因子平衡局部开发和全局探索能力,并通过位置更新公式(式(14))提升算法收敛速度,缩短训练时间。然后选取3个不同MLP结构的分类问题:XOR问题、Iris分类问题和HD分类问题进行实验,用于评估改进灰狼优化算法的优化性能和鲁棒性。实验结果表明,与几个经典智能算法相比,本文IGWO算法训练的MLP,在分类准确率和收敛精度方面具有更好的性能,同时具有较好的鲁棒性。虽然BBO算法的稳定性很高,是最好的,但是其收敛结果不如IGWO算法的。并且在训练器所用时间上,IGWO算法作为训练器时,其并不会因为节点数的增加而导致训练时间大幅增加。同时,面对高维解空间时柯西变异算子对局部探索能力的提升依然有效,余弦因子和更新公式(式(14))保证了算法鲁棒性,结合了这些改进的IGWO算法是一个优秀的MLP训练器。
4 基于柯西变异灰狼优化算法训练的多层感知器

5 实验结果和讨论
5.1 测试问题及实验设置
5.2 XOR问题
5.3 Iris问题
5.4 HD问题


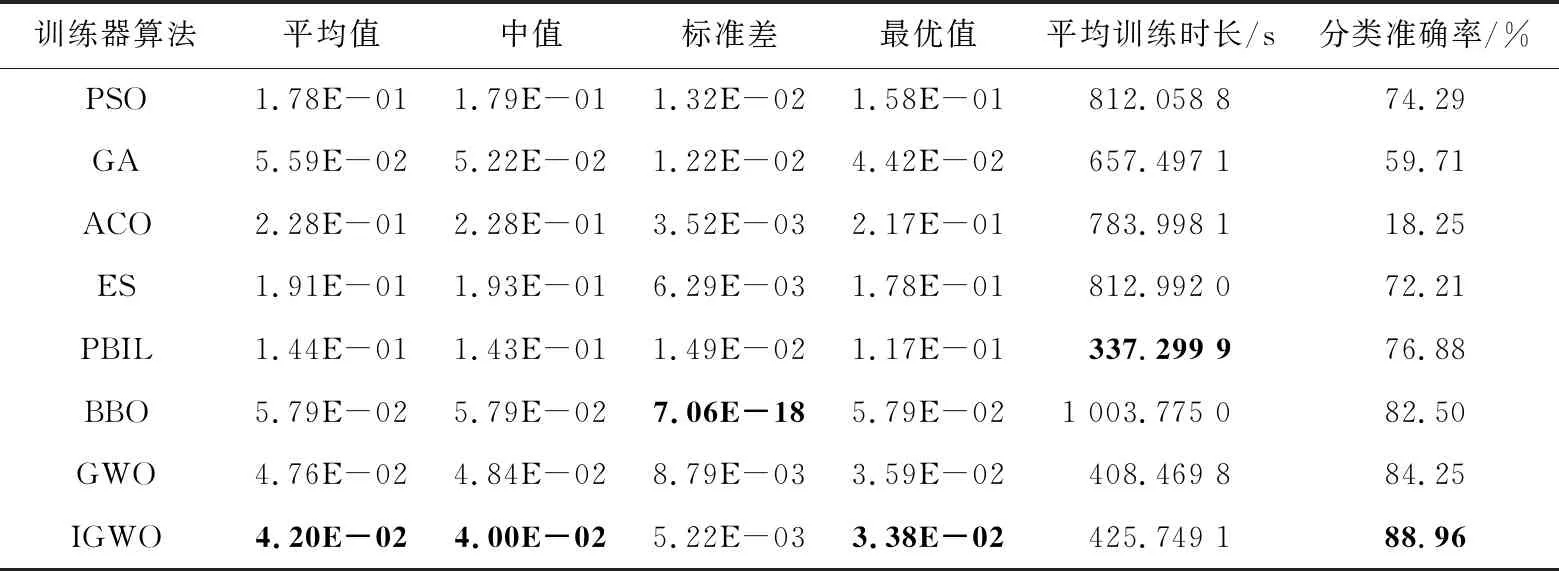

5.5 IGWO算子性能分析


6 结束语
