k最近邻流序列算法对异常流检测的优化研究*

刘 云，王梓宇

(昆明理工大学信息工程与自动化学院，云南 昆明 650500)

1 引言

时空数据包含了与时空维度有关的信息[1]，时空异常检测是时空数据挖掘的一个研究方向[2,3]。随着网络和传感器的普及，时空数据呈现指数级增长，数据流在城市交通数据中较为常见。异常的流值由现实中的某些情况(如过饱和条件[4]和交通拥堵[5])引发，为了发现这些异常值所代表的异常行为，检测城市交通数据中的异常流受到广泛关注[6]。

目前研究人员已经提出了一些用于城市交通流数据的异常检测方法，根据研究内容不同这些方法可以分为统计方法、基于相似度的方法和基于频繁模式挖掘的方法。统计方法使用统计模型(如高斯聚合模型[7]、狄利克雷过程混合模型[8])或诸如主成分分析[9]、随机梯度下降[10]等技术假设正常流遵循某种常规统计过程，而偏离该统计机制的流则视为异常。基于相似度的方法使用距离度量和邻域计算方法或者经典的异常值检测方法[11]来检测异常值。通常情况下，正常的流假定构建密集区域而异常流假定构建低密度区域。基于频繁模式挖掘的方法通过使用诸如Apriori[12]或FP-growth[13]之类的技术来发现异常值之间的关联关系。

相较于检测单个的异常流，检测异常流分布是另一个重要的研究方向[1]。由于基于相似度的方法不考虑流数据之间的相关性而仅适用于检测单个异常流，因此，统计方法是检测异常流分布的一种常用方法。Ngan等人[14]使用一个狄利克雷过程混合模型DPMM(Dirichlet Process Mixture Model)来推导城市交通流数据中的异常值。首先将所有流值的集合F={f1,f2,…,f|F|}映射到一个n维协方差信号描述符中，其中第i个对象由流值{fi,…,fi+n-1}定义，随后通过主成分分析将得到的维度缩小为二维，最后用一个塌陷吉布斯采样器检测流数据中的异常值。由于塌陷吉布斯采样器在大规模数据上的低效率和输出不稳定，使用DPMM的算法(以下称为DPMM算法)有一定的局限性。Ye等人[15]提出了一种称为同时估计流量矩阵并检测异常SETMADA(Simultaneously Estimate Traffic Matrix And Detect Anomaly)的容错流量矩阵估计算法。首先利用流量矩阵的先验低秩属性和时间特性，将流量矩阵异常估计公式转化为一个先验信息引导矩阵完成PigMaC(Prior information guided Matrix Completion)问题，通过采用多块交替方向乘子法ADMM(Alternating Direction Method of Multipliers)以及随机近端梯度下降法来解决该问题，从而实现流量矩阵的异常估计。该算法在估计缺失值时需要考虑很多先验信息，然而在许多领域中先验参数模型是未知的，因此该算法的应用场景有一定的局限性。

为了提高从流序列中检测异常流分布的速度和精度，本文提出了k最近邻流序列算法kNNFS(kNearest Neighbor for Flow Sequence)。算法首先确定每个位置处需要测定的时间区间并计算每个时间区间内的单个流观测值；随后每个时间区间的流分布概率FDP(Flow Distribution Probability)库通过计算单个流的观测频率构建得到；最后使用KL散度计算新的流分布概率与其k最近邻之间的距离，由阈值判定该流分布概率是否异常，如距离值小于阈值则更新入历史流分布概率库，否则作为异常的流分布提取出来。仿真结果表明，与DPMM算法和SETMADA算法相比，kNNFS算法在精度和运行时间方面均有优化提升。

2 模型

城市特定位置处的交通流通过计算一个时间区间内的对象(汽车、出租车和公共汽车等)数量得到[16,17]。交通流数据通常基于某一特定位置在时间区间内表现出某种特定的分布，因此，区别于从交通流的时间序列中检测某一时间区间内的单个异常流，从流序列中检测出的异常流分布更能代表对某段时间区间内总体交通行为产生影响的异常情况。

为了从大规模的城市交通数据中准确快速检测出异常流分布，本文构建了流分布概率这一模型。把流分布概率视为对流及其概率的序列，流值为某个位置处确定时间区间内的对象数，通过构建流分布概率库并使用异常值检测方法计算流分布概率之间的距离。在面对大规模的城市交通数据时，相较检测单个异常流的方法，对流分布概率进行异常检测能极大减少算法的运行时间。同时，通过把检测到的非异常的流分布概率更新入历史流数据库可以不断提高算法的检测精度。k最近邻流序列检测算法框架如图1所示，包括如下2个部分：

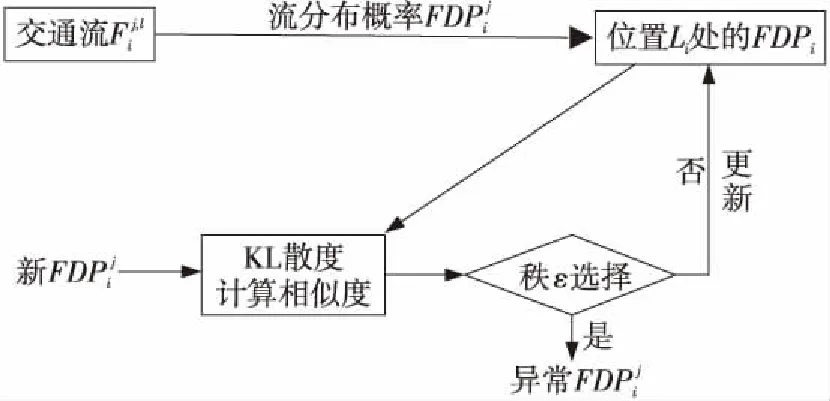
Figure 1 Framework for flow sequences detection algorithm

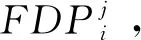
(2)异常值的检测：独立使用历史流分布概率从流式传输的新的流分布中检测异常值。如果新数据不是异常数据，将其更新入历史流分布概率库中，否则将其提取出以待进一步分析。

3 kNNFS算法

3.1 算法推导

算法输入为时空交通流TF，包含时间、位置和交通流值等信息。基于交通流中的位置信息把TF依据位置划分为不同位置处交通流的集合TF={TF1,…,TFn}，上述所有n个位置由位置集合L={L1,…,Ln}表示，TFi是与对应位置Li相关的交通流信息。

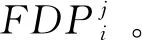
(1)

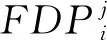
(l-1))),(Tj-1+(TFOi×l))]}

(2)

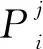
(3)

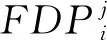
(4)

(5)

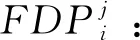
(6)

将得到的所有时间区间的流分布概率组成集合，从而构成位置Li处的流分布概率库FDPi：

(7)

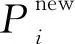
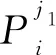
(8)

(9)

(10)

最后，用KL散度计算这2个流分布概率之间的距离相似度，如式(11)所示：

(11)

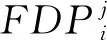
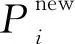
算法1kNNFS算法

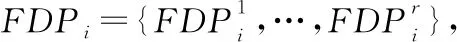
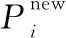
1forj=1 tordo

3endfor

4d←kNN(dist);

5ifd≤εthen

6Anomaly←false

7else

8Anomaly←true

9endif

10returnAnomaly

3.2 算法分析

算法1的理论复杂度分为FDP构建复杂度和异常值检测复杂度2部分：

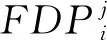
因此，本文所提算法的理论复杂度为：

(12)

其中n为位置Li的数量。

4 仿真分析

4.1 评价指标

为评估kNNFS算法的精度和运行时间，本文在1个中小型交通数据集和1个大型交通数据集上把该算法与其他基准算法进行仿真对比分析。首先在中小型交通数据集上分析比较kNNFS算法、SETMADA算法和DPMM算法检测到异常值的百分比，通过百分比的大小初步说明kNNFS算法的可行性与精度；随后在大型交通数据集上分析比较kNNFS算法与基准算法SETMADA和DPMM的精度和运行时间。本文使用F值来对3种算法进行精度对比分析：

(13)

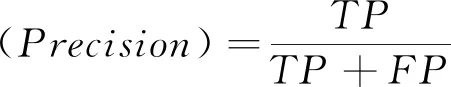
(14)

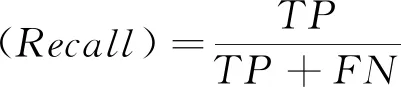
(15)

其中，TP表示正确判属异常流的数量，FP表示错误判属异常流的数量，FN表示错误判定为非异常流的数量。

4.2 数据集

其他类似算法所采用的标准数据集一致，本文依据1个中小型数据集和1个大型数据集来评估算法的性能。第1个中小型数据集是于2017年1月1日至2017年9月30日间在丹麦欧登塞市的7个位置处观测到的真实交通流[20]，数据集概要如表1所示。数据包括在特定位置处检测的车辆的位置、日期时间和速度等信息。位置由经纬度表示；日期时间由汽车经过指定位置的年、月、日、时、分、秒表示，格式为YYYY-MM-DD hh:mm:ss；速度以km/h计算。

第2个大型数据集是在2009年的2个月时间内于中国北京的同一位置处观测到的9亿多个真实城市交通流数据[21]。观测到每台车辆的重要信息包括日期和时间，由汽车经过指定位置的年、月、日、时、分、秒表示，格式为YYYY-MM-DD hh:mm:ss。

Table 1 Feature description of the dataset from Odense Denmark

4.3 欧登塞市数据的仿真结果

从图2中可以看出，在丹麦欧登塞市的7个位置处,kNNFS算法、SETMADA算法和DPMM算法检测到的异常值的百分比均高于70%。在非密集型位置L1、L2、L3和L4处,kNNFS算法和SETMADA算法以及DPMM算法检测到的异常值的百分比均在75%附近；在密集型位置L5、L6和L7处，可以看出kNNFS算法检测到的异常值的百分比在85%附近，明显高于SETMADA算法和DPMM算法的。

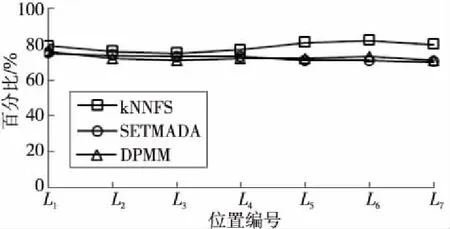
Figure 2 Percentage of detected outliers at different locations

可见，kNNFS算法、SETMADA算法和DPMM算法均适用于在中小型交通数据集中检测异常值。对于非密集型位置，kNNFS算法的精度与SETMADA算法和DPMM算法的相当；对于密集型位置，kNNFS算法的精度较SETMADA算法和DPMM算法有明显提升。上述提升得益于kNNFS算法采用的KL散度距离更适用于计算分布之间的相似度，同时本文提出的算法把新的非异常FDP更新入历史FDP库，有利于提高检测异常值的精度，并且在数据较密集(数据集规模较大)时这种提升效果更为明显。

4.4 北京市数据的仿真结果

从图3中可以看出，在大型交通数据集上仿真时，随着流量值从4亿逐渐增加至9亿，kNNFS算法的F值逐渐升高，而SETMADA算法和DPMM算法的F值逐渐降低。同时，不论流量值为4亿～9亿间的何值，除取值4亿时3种算法的F值均近似于0.8以外，其余取值时kNNFS算法的F值都明显高于SETMADA算法和DPMM算法的。其中，当流量值为最大9亿时,kNNFS算法的F值高于0.9，明显优于SETMADA算法和DPMM算法的0.7附近的水平。

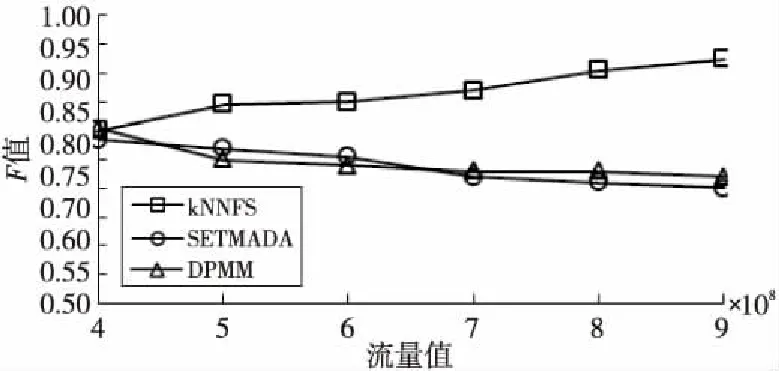
Figure 3 F-measure on different numbers of flow data

可见，当流量值大于4亿时，kNNFS算法的精度明显高于SETMADA算法和DPMM算法的。上述差异的原因在于，随着大型交通数据集中流量值逐渐增大，算法计算的样本数量逐渐增多，由于kNNFS算法将新的非异常FDP更新入历史FDP库，其精度会逐渐升高，而SETMADA算法和DPMM算法由于计算量过于巨大，其精度反而逐渐降低。

从图4中可以看出，在大型交通数据集上仿真时，随着流量值从4亿逐渐增加至9亿，3种算法的运行时间都逐渐增加。不论流量值为4亿～9亿间的何值，kNNFS算法的运行时间都明显少于SETMADA算法和DPMM算法的。其中，当流量值为4亿时，kNNFS算法的运行时间在1 500 s附近，明显低于SETMADA算法的1 800 s附近以及DPMM算法的2 000 s附近的水平；当流量值为9亿时，kNNFS算法的运行时间在2 000 s附近，明显低于SETMADA算法的2 500 s附近以及DPMM算法的3 000 s附近的水平。

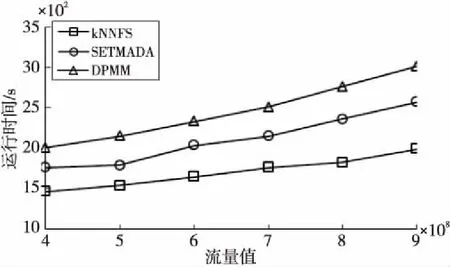
Figure 4 Runtime on different number of flow data

可见，在大型交通数据集上,kNNFS算法由于使用了FDP库，其运算速度明显优于SETMADA算法和DPMM算法的。进一步分析得出，当流量值从4亿增加至9亿时，流量增加了1.25倍，kNNFS算法的运行时间增加了33%，而SETMADA算法运行时间增加了39%,DPMM算法运行时间增加了50%。因此，随着流量值逐渐增加，kNNFS算法运行时间的增加幅度也要小于SETMADA算法和DPMM算法的。

5 结束语

为了提高检测流序列中的异常流分布的速度和精度，本文提出了k最近邻流序列算法(kNNFS)。划分时间区间后为每个位置测定每个时间区间内的单个流观测值，通过计算单个流的观测次数和频率构建流分布概率(FDP)库，随后由KL散度计算新输入的流分布概率与其k最近邻之间的距离，最后由阈值判定新的流分布概率是否异常，距离值小于阈值则更新入历史流分布概率库，否则为异常值。仿真结果表明，kNNFS算法在精度和运行时间方面均有优化提升。由于使用了k最近邻，算法对邻域数量和挖掘阈值敏感，为这2个参数选择合适的值对算法的精度至关重要。下一步工作的主要方向是消除参数使用的估计偏差来提高算法的检测性能。