一种改进的OSID的图像匹配算法*

陈雪松，雷 嫚，毕 波，唐锦萍

(1.东北石油大学电气信息工程学院，黑龙江 大庆 163318；2.东北石油大学数学与统计学院，黑龙江 大庆 163318;3.海南医学院公共卫生学院，海南 海口 571101;4.黑龙江大学数据科学与技术学院，黑龙江 哈尔滨 150080)

1 引言

尽管 SIFT(Scale Invariant Feature Transform)算法的关键点检测器及描述符[1 - 4]已有十几年的历史，在很多基于视觉特性的应用中，包括对象识别[1]、图像拼接[5]和图像映射[6]等，都非常成功，但它也伴随着大量的计算负担，尤其是对于实时系统而言，例如视觉测定器或者低功耗设备手机等，因此需要找到计算成本较低的替代方案。而且随着科学技术的进步，数据处理的需求也日益增加，对算法的复杂性和鲁棒性要求也越来越高，对于低复杂度、低存储空间的特征描述算法的需求也越来越迫切。所以，研究人员已经开始对高维浮点型描述子进行降维处理。

于是二进制位串描述子就产生了，它和实值描述子最大的不同就是，不是采用欧氏距离作为度量距离，而是采用汉明距离，其优点就是计算量比欧氏距离的小。

2013年，Wang等[7]采用一种新的快速鲁棒不变特征FRIF (Fast Robust Invariant Feature)进行特征检测和描述。其基本思想是利用快速逼近的Log检测器来选择尺度不变的关键点，并结合局部模式和模式间信息来构造独特的二进制描述符。2014年，Xu等[8]提出了区域不变量的序数和空间信息OSRI(Ordinal and Spatial Information of Regional Invariants)算法，该算法将特征点的局部邻域扩展到多层范围，并对每层邻域按像素强度值和梯度方向顺序划分为多层子区域；按圆形区域中的像素强度值或者梯度方向值将划分范围进行多次旋转(移位)，构建多组层的子区域集合；最后通过子区域中多种不变特征的比较结果形成二进制描述向量。2016年，谭跃生等[9]针对传统局部特征提取算法在提取特征点时效率不高,生成描述子需要计算主方向等问题,结合SURF(Speeded-Up Robust Features)算法和RGT(Radial Gra- dient Transform)[10],在精度损失尽可能小的情况下提高局部不变特征提取速度,提出一种改进的加速径向SURF算法AR-SURF。实验结果表明,AR-SURF算法节省了时空损耗,提升了定位速度,提取效果更好,更加适合海量图像处理。2018年，于达[11]对目前常用的局部不变特征匹配算法进行研究,分析比较各算法的旋转不变性、尺度不变性、定位精度和匹配效率。利用Grab Cut算法对识别出的目标物体进行图像分割,针对图像分割过程中需要人机交互的问题,将特征匹配算法与图像分割算法连接起来,提高算法的自动化程度。其次,在完成目标物体图像分割的基础上,基于图像矩计算出目标的质心,利用极线约束提高质心匹配效率。2019年，赵爱罡等[12]提出了一种基于两层策略的特征点匹配方法。首先根据特征点响应的阈值对实时图和参考图分别提取一级特征点和二级特征点,然后依据二级特征点到一级特征点的距离使二级特征点隶属于距离最近的一级特征点,由此达到对二级特征点进行分组的目的。仿真实验结果表明,特征点匹配速度大幅提升。

本文提出的特征建立在最近开发的一种基于旋转的快速提取特征的描述子ORB (Oriented FAST and Rotated BRIEF)[13,14]特征检测和序数空间强度分布OSID(Ordinal Spatial Intensity Distribution)[15]描述子上。由于它们的优良性能和低成本，这2种技术都是有吸引力的。本文讨论了SIFT技术和OSID的几个局限性，其中最明显的是匹配时间成本高。

2 序数空间强度分布

OSID的特征描述子的主要思想是在亮度逐渐增加的情况下，局部块像素强度的相对顺序保持不变或稳定。OSID是通过对二维直方图进行栅格化来构造的，在序数空间和空间强度中对像素分组(或组合)。在序数空间中对像素进行绑定，可以确保特征不受复杂亮度变化的影响，同时在空间上绑定像素可以捕获图像块的结构信息：如果特征是从像素的朴素直方图中获得的，就会丢失。为了提取特征及其描述子，通过预处理步骤和特征检测步骤对特征点进行定位。

2.1 预处理与特征检测

在计算特征之前，目标图像和配准图像需要用高斯滤波器进行平滑处理，以达到消除噪声的目的，因为像素强度的相对顺序可能对噪声很敏感。所以，要为特征点划分局部区域， 具体过程为：对于每个检测到的特征点，提取大小为d*d的局部块，其中d的典型选择为41，但它可能随图像分辨率和尺度的变化而变化。

2.2 序号和空间标号

对于序数分布，块中的像素被分组到n个箱子中，每个箱子中的像素都具有相似的像素强度。与具有n个箱子的常规直方图不同，每个箱子表示顺序范围，而不是原始像素强度的范围，因为原始像素可能由于帧的变化导致像素值发生改变。像素被标记为它们所属的箱号。在空间分布中，d*d图像块中的像素基于n个扇形空间细分来标记。将像素分配给子图像块是预先计算的，以节省计算时间。

2.3 二维直方图和栅格化

为每个局部块创建一个二维直方图，其中，直方图中的x轴表示按相对顺序编码的像素强度，y轴表示空间分布。在二维直方图中，位置(x,y)处的数值表示在y细分区域中像素点的个数，像素点的排序为x。

二维直方图中的每一行都是一维直方图，它表示像素在给定子块的序号空间中的分布情况。它是一个n维向量，每个维表示有多少像素具有序号空间标签。二维直方图中的每一列表示相似强度的像素在子块中的分布情况。

在为每个图像块构造了有序空间的二维直方图之后，需要对图像中每个图像块构造的直方图进行栅格化处理，形成一个n*m维向量作为d*d块的描述符。栅格化的起始库和方向(或顺序)可以是任意的，但是需要预先定义。最后，根据块中的像素个数对特征向量进行归一化处理，消除特征向量对描述符的影响。因此，图像块的大小可能因特征点的不同而不同。OSID描述符的具体步骤如图1所示。

Figure 1 Workflow of OSID descriptor

3 改进的OSID算法

本节首先介绍改进OSID精度的方法，对OSID描述子进行改进，OSID描述符构建的过程中，根据关键点信息(像素强度)区域的密集程度设置m的值，并对描述子的表现形式进行转换，将直方图描述子转换为二进制描述子，提高算法运行速度。

3.1 对OSID描述子的改进

OSID将强度顺序信息编码为描述符，然后对局部图像块中不同子区域的强度顺序的直方图进行计算。这是OSID描述符的基本思想。简单地说，它既捕获了局部图像块中像素的序数分布，又捕获了像素的空间分布，并使用它们的联合分布作为特征描述符。具体来说，在特征点周围取一个41*41大小的图像块，将图像块分成16个等大的扇形，再对每个扇形内的像素进行排序，并放入8个箱子中(0～32，32～64，…,223～255)，每个特征点生成16*8的直方图子描述子，将每个特征点的子描述子连接构成OSID描述子。然后，在特征点41*41图像块范围内，可能存在其他特征点，为更好地表达多个特征点的图像块信息，本文提出将m(扇形个数)自适应，在保证图像信息的前提下节省储存空间并提高算法计算速度。

快速检测特征点算法FAST(Features from Accelerated Segment Test)[16,17]的提出者Rosten等将FAST的原理表述为：若某像素与其周围邻域内足够多的像素点相差较大，则该像素可能是角点。ORB描述子的特征提取是由FAST算法改进的，称为oFAST(FAST Keypoint Orientation)[9]，即在使用FAST提取出特征点之后，给其定义一个特征点方向，以此来实现特征点的旋转不变性。本文使用ORB算法检测特征点，再对特征点构建描述子；在构建描述子的过程中，一个特征点的图像块里有多个特征点，则这个图像块中有多个像素点与其周围邻域内足够多的像素点相差较大，本文认为此特征点的局部图像块信息较为丰富，因此考虑将此局部图像块进行更细化的处理，增加扇形个数m，以更好地表达该区域图像块的信息。

OSID描述符构建的过程中，图像块的扇形个数m的选择是固定的，因此本文尝试将扇形个数的值自适应，对特征点个数大于1的区域的m设置得更大，以保证图像块的信息被更好地表达，对特征点个数小于或等于1的区域的m设置得更小，在保证图像信息能够被表达的前提下节省储存空间并提高算法速度。具体步骤：当某个特征点的41*41图像块内除它本身外另有1～2个特征点时，将扇形个数设置为18；当某个特征点的41*41图像块内除它本身外另有3～4个特征点时，将扇形个数设置为20；当某个特征点的41*41图像块内除它本身外另有5个以上特征点时，将扇形个数设置为22。

3.2 对OSID匹配效果的改进

OSID最后生成的描述子是直方图描述子。对每个特征点局部块都创建一个二维直方图，其中，直方图中的x轴按照像素强度的相对顺序编码像素强度分布，y轴编码空间分布。在为每个图像块构造了有序空间的二维直方图之后，对直方图进行栅格化，形成一个n*m维向量作为d*d块的描述符。然后，根据块中的像素个数对特征向量进行归一化处理，消除特征向量对描述符的影响。因此，图像块的大小可能因特征点的不同而不同。

由于目标图像和配准图像中的每一个特征点都会生成一个直方图描述子，因此在图像匹配的过程中，目标图像中的任一直方图描述子都需要与配准图像中的所有直方图描述子进行欧氏距离的计算，将欧氏距离数值最小的直方图描述子对应的特征点判定为匹配特征点，因此计算复杂度高，运算时间长。二进制描述符比传统描述符(即浮点向量描述符)所需的存储空间要小得多。同时，计算用于评估二进制描述符之间的相似度的汉明距离比计算浮点向量描述符之间的欧氏距离快得多。因此，二进制描述符正在成为需要实时处理或内存资源有限的应用程序的流行解决方案。

在此，本文将直方图描述子编码为二进制描述子，当生成改进OSID的直方图描述子后，首先比较直方图中直方条的数值 ：(1)当前直方条数值大于或等于后一个直方条数值时记为1，否则记为0；(2)直方图最后一个直方条的数值与第一个直方条的数值进行比较，以保证描述子转换后的二进制描述符维度与直方图维度相同。这样，每个特征点的局部图像块描述子就编码成了二进制描述子，最后用汉明距离匹配特征点。

4 实验

4.1 数据集

本文在标准数据集[18]上与多个著名的描述符进行性能比较，该数据集包含具有不同几何和光度转换的真实图像(例如，视点变化、图像模糊、JPEG压缩)，本文对参考图像(第1幅图像)与相比变化较大的第4幅图像，以及变化最大的第6幅图像进行对比(对像素强度进行归一化，使其最大值为1)。

4.2 实验结果

实验平台和环境为CPU 1.8 GHz，内存4 GB，Windows 7系统，Python 3.7.6，将本文算法与OSID算法、SIFT算法、SURF算法[19,20]、BRISK(Binary Robust Invariant Scalable Keypoints)算法[21 - 23]、改进ORB算法[24]和FAST算法在准确率和运行时间上进行对比。在每个数据集上给出3个算法的匹配连线图，分别是改进OSID算法、除改进OSID算法外准确率最高的算法和除改进OSID算法外准确率最低的算法。

(1)视点更改。改进OSID描述符在wall数据集上进行了视点更改测试,结果如表1和表2所示。表1和表2为7种算法准确率和运行时间的对比，其中找到的特征点数包含2个数值，分别是目标图像中的特征点数和配准图像中的特征点数。

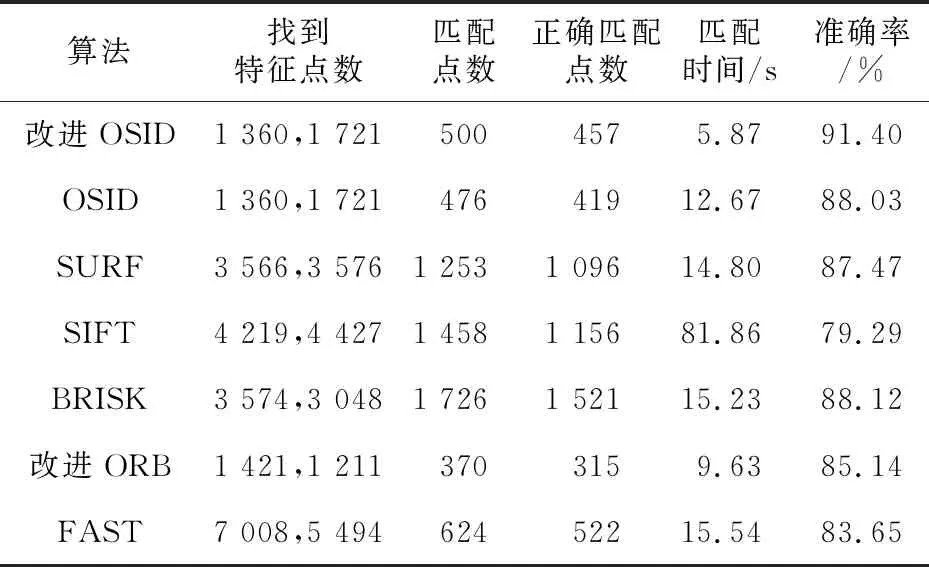
Table 1 Comparison of matching performance between the first and fourth images on wall dataset

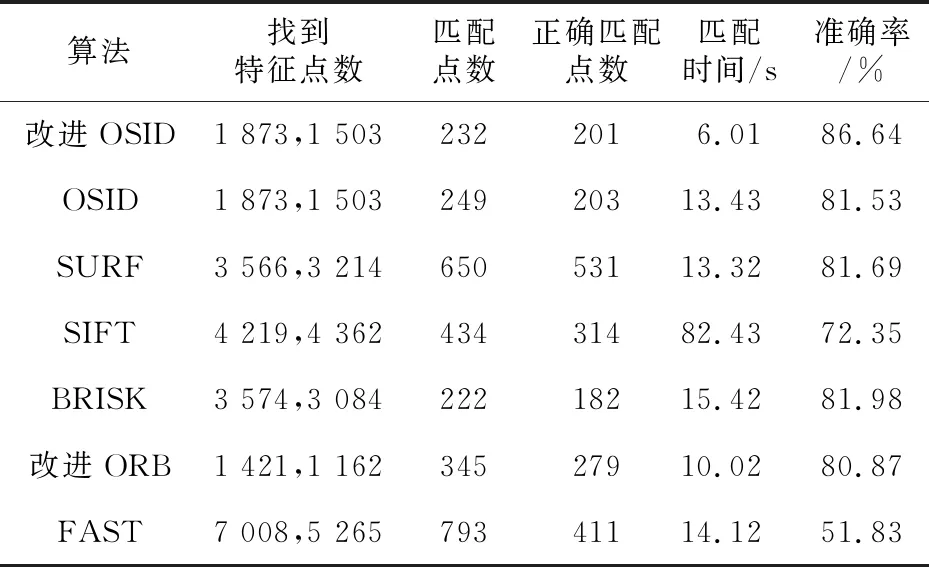
Table 2 Comparison of matching performance between the first and sixth images in the wall dataset

由表1可以看出，由于改进OSID算法的特征点检测部分与原算法一样，所以二者找到的特征点数一样，原算法准确率只有88.03%，运行时间为12.67 s。FAST算法找到的特征点数最多，但错误匹配点数量也最多，正确匹配率为83.65%，SIFT、SURF和BRISK算法找到的特征点数次之，改进ORB算法找到的特征点数较少，运行速度相对于SURF、BRISK和FAST算法较快。但是，改进后OSID算法找到的特征点数最少，误匹配数量也最少，准确率为91.40%，运行时间为5.87 s。比SURF、BRISK、FAST和改进ORB等算法快5 s以上，比SIFT快70多秒。BRISK算法匹配点数最多，准确率为88.12%。由表2可以看出，在严重的视点变化时本文算法与对比算法的正确匹配率都有所下降，尤其是FAST算法，准确率只有51.83%，6种对比算法的表现也有所下降，但本文算法依然表现良好，准确率为86.64%，运行时间为6.01 s。可以看到，本文改进的描述子不管是在适当数量的视点变化时还是在严重的视点变化时表现得都很好。

由图2～图4可以直观地看出，在wall数据集的第1幅与第4幅图像匹配性能对比中，本文改进后的OSID算法匹配效果最好，BRISK算法次之，SIFT算法的匹配连线混乱，准确率最低。而由图5～图7观察到，在wall数据集的第1幅与第6幅图像匹配性能对比中，视角变化很大，本文改进后的OSID算法匹配效果虽然准确率有所下降，但依然是表现最好的，BRISK算法依旧次之，而FAST算法的匹配连线混乱，准确率最低。

Figure 2 Line matching diagram of the first and fourth images in wall dataset using improved OSID algorithm

Figure 3 Line matching diagram of the first and fourth images in wall dataset using BRISK algorithm

Figure 4 Line matching diagram of the first and fourth images in wall dataset using SIFT algorithm

Figure 5 Line matching diagram of the first and sixth images in wall dataset using improved OSID algorithm

Figure 6 Line matching diagram of the first and sixth images in wall dataset using BRISK algorithm

Figure 7 Line matching diagram of the first and sixth images in wall dataset using FAST algorithm

(2)图像模糊。本文也在bikes数据集的模糊图像上进行了描述符测试，结果如表3和表4所示，FAST、SIFT、SURF和BRISK等算法找到的特征点数都较多，但错误匹配点数量也较多，且在图像模糊程度高时，SIFT、BRISK和改进ORB算法的表现也有所下降。原算法匹配点数和改进OSID的差不多，但是准确率低于改进OSID算法的。改进后的OSID算法在图像模糊程度较高时准确率虽然也有所下降，但总体表现良好。可以观察到，虽然改进OSID算法不是为了解决图像模糊问题而提出的， 但是它也表现得比其他描述子优异。

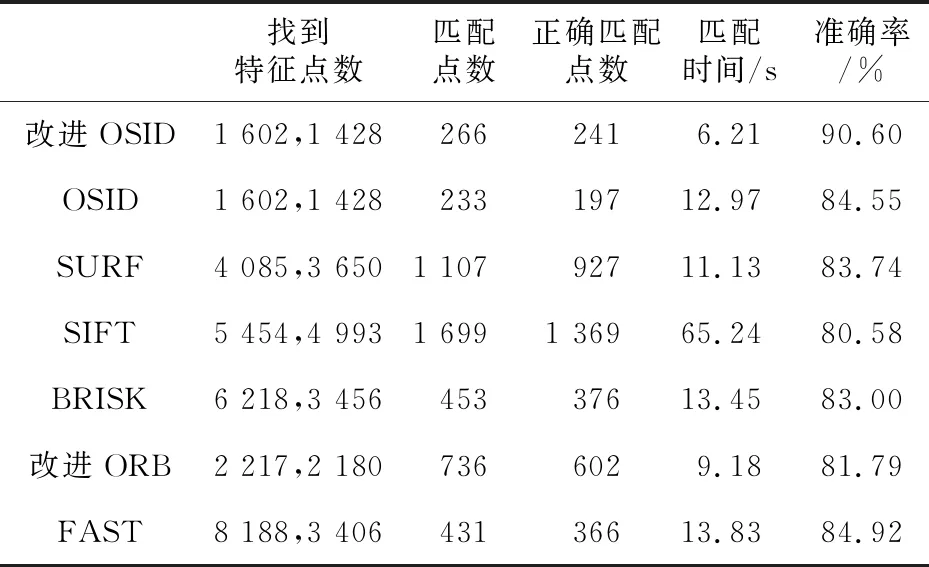
Table 3 Comparison of matching performance between the first and the fourth images on bikes dataset

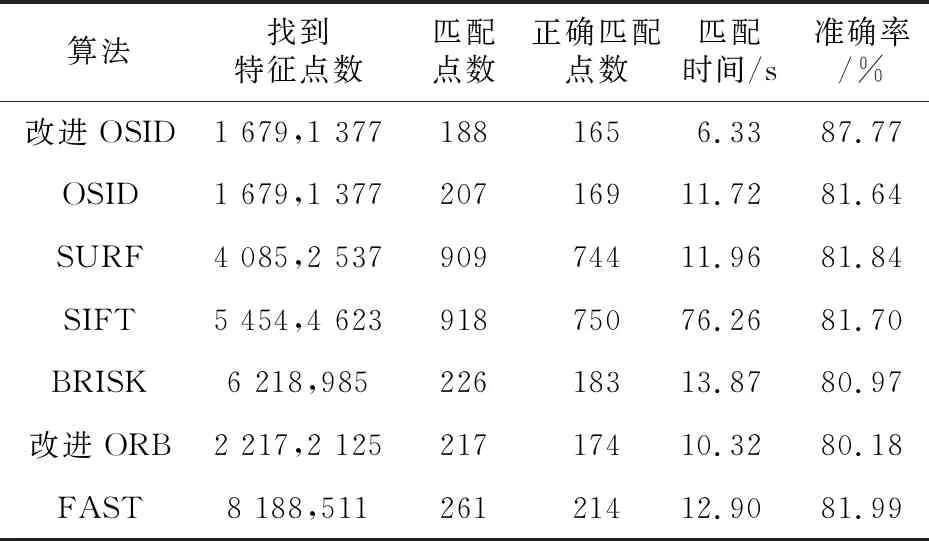
Table 4 Comparison of matching performance between the first and the sixth images on bikes dataset

由图8～图10可以直观地看出，在bikes数据集的第1幅与第4幅图像匹配性能对比中，本文改进后的OSID算法匹配效果明显良好，FAST算法居于第2，SIFT算法匹配效果最差。而由图11～图13观察到，在bikes数据集的第1幅与第6幅图像匹配性能对比中，模糊程度较高，本文改进后的OSID算法匹配效果依然表现良好，FAST算法依旧次之，而BRISK算法的匹配连线杂乱，准确率最低。

Figure 8 Line matching diagram of the first and fourth images in bikes dataset using improved OSID algorithm

Figure 9 Line matching diagram of the first and fourth images in bikes dataset using FAST algorithm

Figure 10 Line matching diagram of the first and fourth images in bikes dataset using SIFT algorithm

Figure 11 Line matching diagram of the first and sixth images in bikes dataset using improved OSID algorithm

Figure 12 Line matching diagram of the first and sixth images in bikes dataset using FAST algorithm

Figure 13 Line matching diagram of the first and sixth images in bikes dataset using BRISK algorithm

(3)JPEG压缩。本文也在不同级别的JPEG压缩下使用UBC数据集测试了描述符，结果如表5和表6所示。可以观察出，在不同压缩级别下SIFT算法都表现较好，准确率分别为88.12%和84.37%，但运行时间较慢，而改进后OSID描述子无论在何种压缩级别下运行时间都最快，且在JPEG压缩级别适中的情况下表现最好，在JPEG压缩级别较高的情况下表现良好。

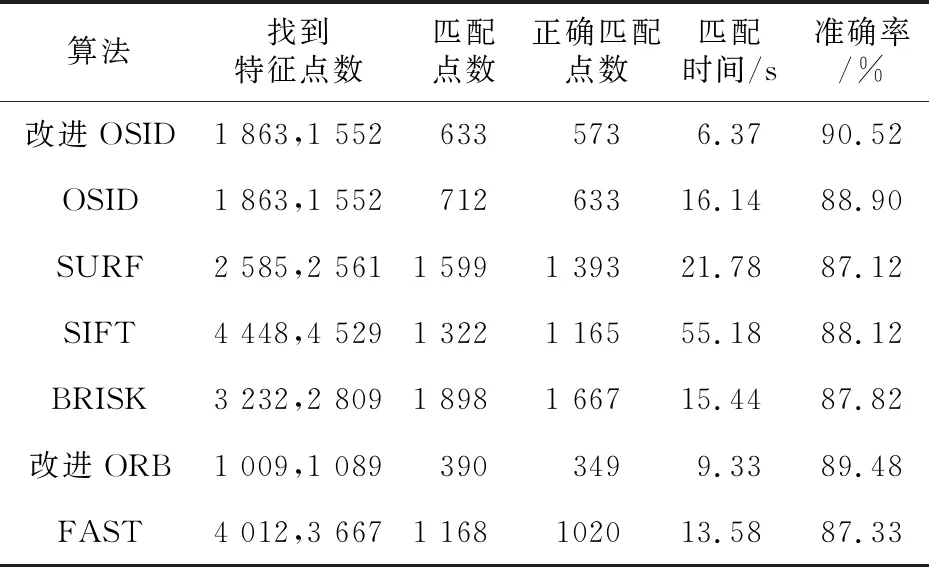
Table 5 Comparison of matching performance between the first and fourth images on UBC dataset

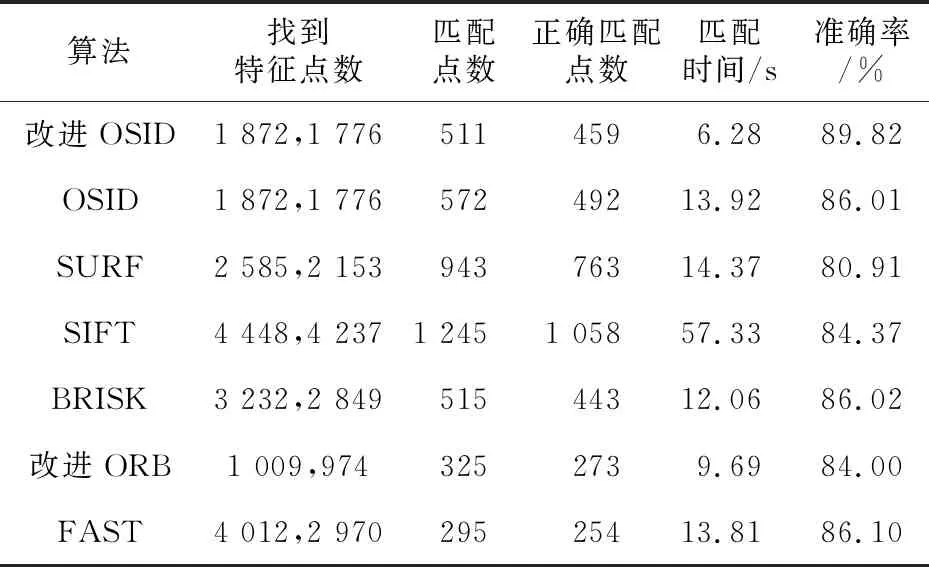
Table 6 Comparison of matching performance between the first and sixth images on UBC dataset

由图14～图16可以直观地看出，在UBC数据集的第1幅与第4幅图像匹配性能对比中，本文改进后的OSID算法匹配效果最优，改进ORB算法次之，SURF算法匹配效果最差。而由图17～图19观察到，在UBC数据集的第1幅与第6幅图像匹配性能对比中，本文改进后的OSID算法和对比算法的准确率都有所下降，但改进OSID算法依然表现良好，FAST算法次之，而SURF算法的匹配连线杂而乱，准确率最低。

Figure 14 Line matching diagram of the first and fourth images in UBC dataset using improved OSID algorithm

Figure 15 Line matching diagram of the first and fourth images in UBC dataset using improved ORB algorithm

Figure 16 Line matching diagram of the first and fourth images in UBC dataset using SURF algorithm

Figure 17 Line matching diagram of the first and sixth images in UBC dataset using improved OSID algorithm

Figure 18 Line matching diagram of the first and sixth images in UBC dataset using FAST algorithm

Figure 19 Line matching diagram of the first and sixth images in UBC dataset using SURF algorithm

5 结束语

针对OSID算法同一个图像块多个特征点、实时性较差的问题，本文提出了一种基于局部二进制模式的快速匹配算法。该算法采用改进的局部二进制模式对ORB特征进行描述，并对构建描述子的扇形个数采用自适应的方法，丰富描述子所包含的信息，提高了算法的准确率。实验表明，本文算法计算复杂度低、鲁棒性好，并且该描述子在复杂视点变化、图像模糊等情况下的特征匹配是非常有效的。下一步将着重考虑对特征点检测的速度与精度进行研究，以进一步提高图像匹配算法性能。