基于ARM SVE的光滑粒子流体动力学SIMD加速方法*
2021-06-25范小康夏泽宇龙思凡杨灿群
范小康,夏泽宇,龙思凡,杨灿群
(国防科技大学计算机学院,湖南 长沙 410073)
1 引言
数值模拟技术是工程应用和科学研究的一个重要手段。与实验手段相比,数值模拟成本低,并且可以模拟很多难以开展实验或无法开展实验的情况,因而受到越来越多研究人员的青睐。光滑粒子流体动力学SPH(Smoothed Particle Hydrodynamics)[1 - 3]方法是一种无网格的粒子方法,近年来逐渐成为数值模拟技术领域的一个研究热点。
传统的数值模拟技术以网格作为基础,将实际问题转化为数学描述的离散形式,即物理控制方程组,然后采用计算机求解。比较具有代表性的方法包括有限差分法FDM(Finite Differential Method)[4]、有限体积法FVM(Finite Volume Method)[5]和有限元法FEM(Finite Element Method)[6],已经在计算流体力学CFD(Computational Fluid Dynamics)和计算固体力学CSM(Computational Solid Mechanics)中取得了广泛应用。传统基于网格的方法存在着固有的缺陷,复杂几何形状的网格构造是一个难点,此外,基于网格的方法也难以处理大变形问题。
近年来,无网格方法受到了越来越多的重视。无网格方法的主要思想是通过使用一系列任意分布的节点或者粒子来求解具有各种各样边界条件的积分方程或偏微分方程组。无网格方法的优点在于免去了网格生成的麻烦,并且避免了网格扭曲与网格重构的问题。SPH是一种无网格的拉格朗日粒子方法,该方法的基本思想是将连续的流体(或固体)用相互作用的质点组来描述,各个质点上承载各种物理量,包括质量、位置坐标、速度等,通过求解质点组的动力学方程和跟踪每个质点的运动轨道,求得整个系统的力学行为。SPH方法的粒子特性使得其在处理大变形、运动物质表面以及自由表面等问题时优势明显,已被诸多商用软件采用。
作为一种粒子方法,SPH方法在每一个迭代步都需要计算大量的粒子间相互作用,如何提高SPH方法的计算效率是目前的研究难点,也具有非常大的实际意义。针对SPH方法的计算效率问题,国内外也开展了大量的研究工作[7 - 11]。作为一种显式求解的粒子方法,SPH天然地适合采用并行结构求解,目前已涌现出大量基于分布式存储的高性能计算平台、共享存储结构的并行SPH计算方法,有效地提高了SPH方法的计算效率,使得SPH可处理的问题规模越来越大。然而,以上方法研究的都是SPH方法中的进程级或线程级并行,却鲜有工作探索SPH方法中的数据级并行。
近年来ARM面向高性能计算推出了可伸缩矢量扩展SVE(Scalable Vector Extension)[12]。SVE并不是ARM NEON的简单扩展,而是基于ARM AArch64架构的下一代SIMD指令集。与NEON相比,SVE可以获得超过7倍的加速比,极大地提升了性能[12]。SVE允许硬件设计师根据应用需求定义向量寄存器宽度,最大可支持2 048位的向量宽度。SVE支持VLA(Vector Length Agnostic)编程方式,编程人员或编译器无需在程序中指定向量宽度,程序被编译成SVE指令后,可在不同向量宽度的CPU上兼容运行,而无需针对不同向量宽度的CPU重新编译。SVE在高性能计算领域拥有非常好的应用前景,比如日本的下一代超级计算机富岳[13,14]就采用了SVE。
SVE引入了一些新的架构特点,包括:(1)可变向量长度:SVE提供32个向量寄存器,向量寄存器长度为128的整数倍,最低128位,最高可支持2 048位;(2)每通道预测(Per-Lane Predication):SVE提供16个预测寄存器(Predicate Register),预测寄存器每一位控制向量寄存器的一个字节,通过预测寄存器中每一位的有效状态来控制向量寄存器中对应元素是否参与运算;(3)聚集取和分散存(Gather-Load,Scatter Store):支持非连续存储数据的高效访问。
SVE提供了比传统SIMD架构更长的向量寄存器,具备更强的计算能力,在SVE上运行的程序理论上可获得更高的性能。本文基于SVE提出了一种SPH的SIMD向量优化方法,利用SVE对SPH方法的关键部分粒子间相互作用的计算开展向量化并行,探索SPH的数据级并行。实验结果表明,采用SVE可以获得粒子间相互作用计算的显著性能提升。
2 背景介绍
SVE是ARM在AArch64架构基础上针对高性能应用所推出的SIMD扩展指令集。ARM为SVE定义了32个向量寄存器和16个预测寄存器。向量寄存器的宽度是128的整数倍,范围从128位~2 048位。预测寄存器的每一位(bit)对应向量寄存器的一个字节(byte),通过不同位的有效性控制向量寄存器中不同元素是否参与向量操作,预测寄存器可以看作是一个控制向量运算的掩码。ARM为SVE引入了VLA编程方式,对于循环的向量化可以实现与处理器向量寄存器宽度无关的控制。
2.1 每通道预测
图1通过一条向量化融合乘加指令(fmla)简要说明基于预测寄存器的向量操作。指令fmla的操作是把向量寄存器z1与z2中的数据相乘,乘积与向量寄存器z0中的数据相加,最后将结果写入向量寄存器z0中。向量寄存器的后缀·d表示寄存器中存放的是双精度浮点(double)类型的操作数。预测寄存器p0/m为合并模式,表示若预测寄存器该有效位无效,则目标寄存器对应通道数据保持原值。3个向量寄存器z0,z1和z2 中参与运算的元素由预测寄存器p0对应的位控制,若对应的位为TRUE(1),则向量寄存器中对应的元素参与运算,如A[7]、A[5]、A[3]、A[1],反之若预测寄存器中对应的位为FALSE(0),则向量寄存器中对应的元素不参与运算,如A[6]、A[4]、A[2]、A[0]。
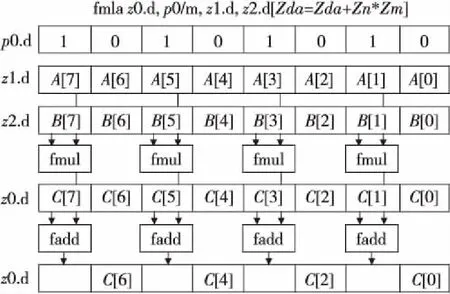
Figure 1 SIMD operation based on predicate register
2.2 VLA
以DAXPY运算为例简要说明VLA编程方式。基于VLA的DAXPY运算代码如下所示:
1 //-------------------------------------------------------------
2 // voiddaxpy(int64_tn,doubleda,double *dx,double *dy) {
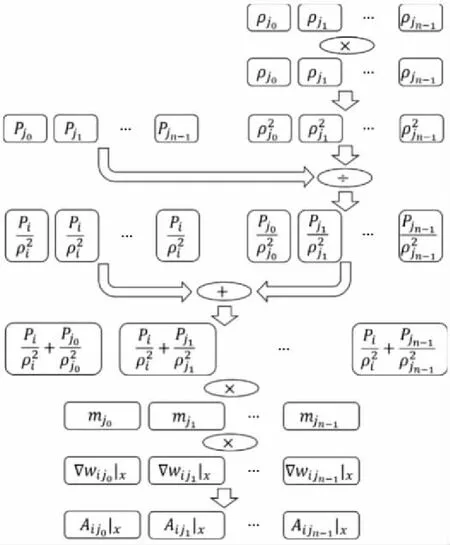
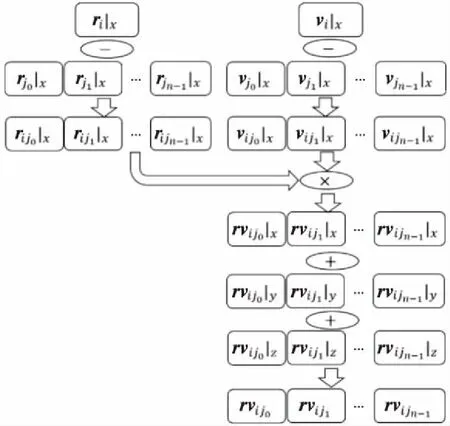
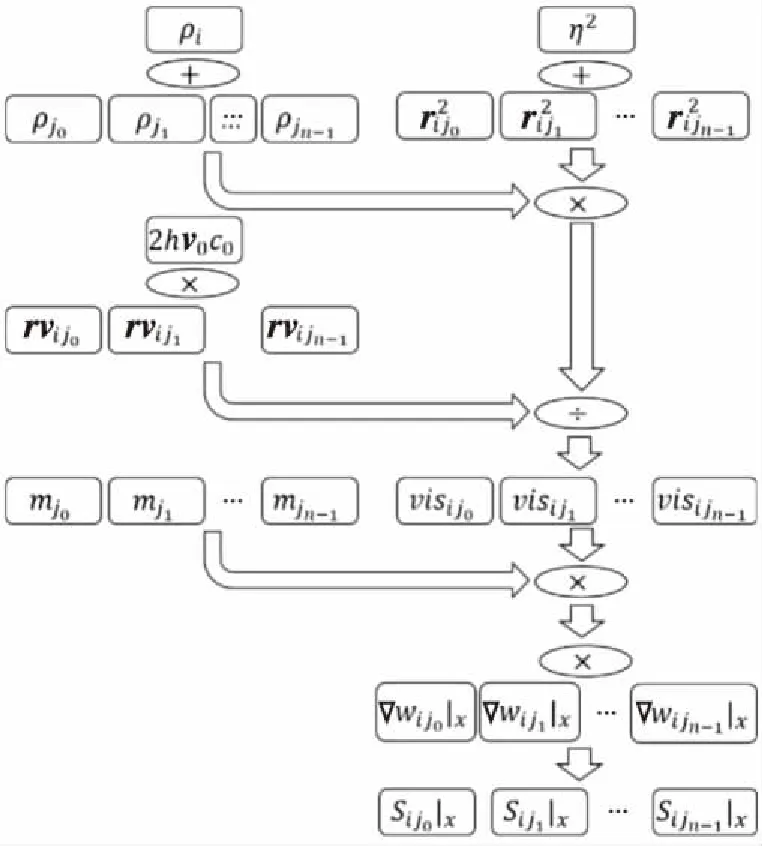
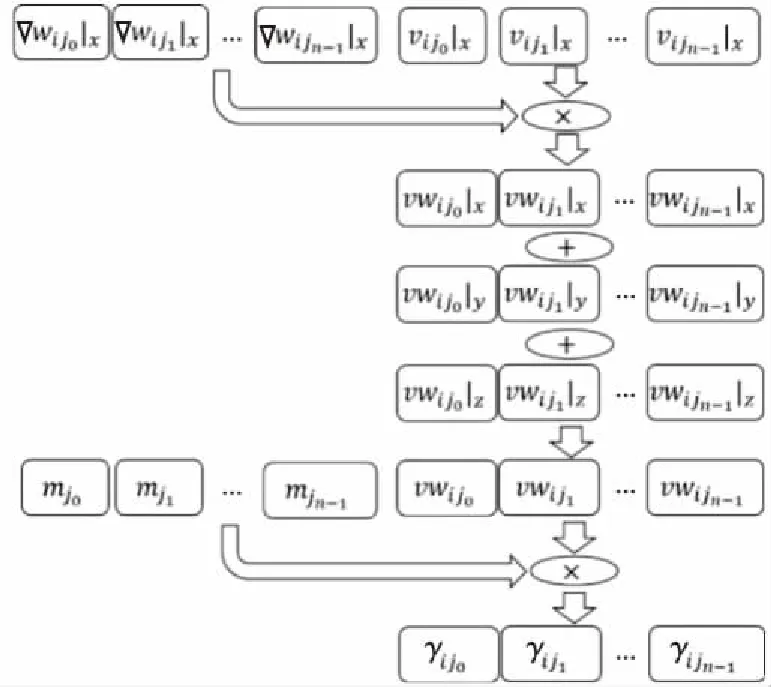
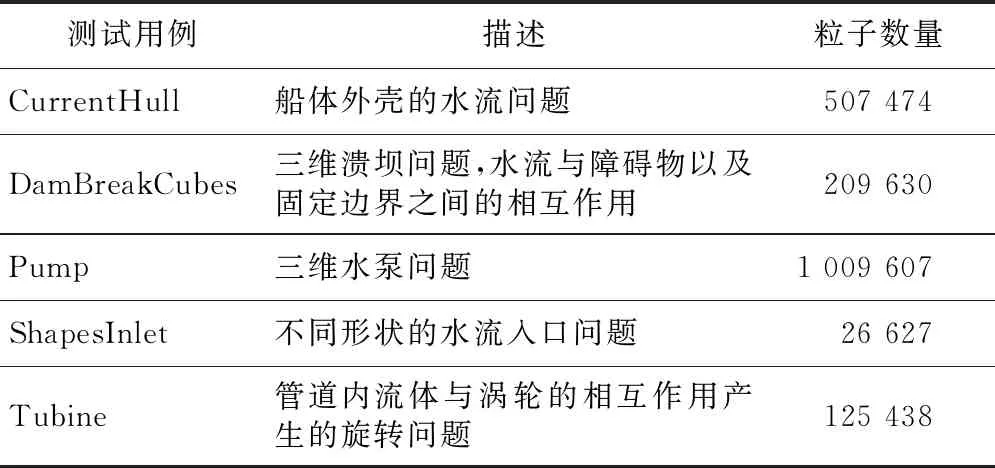
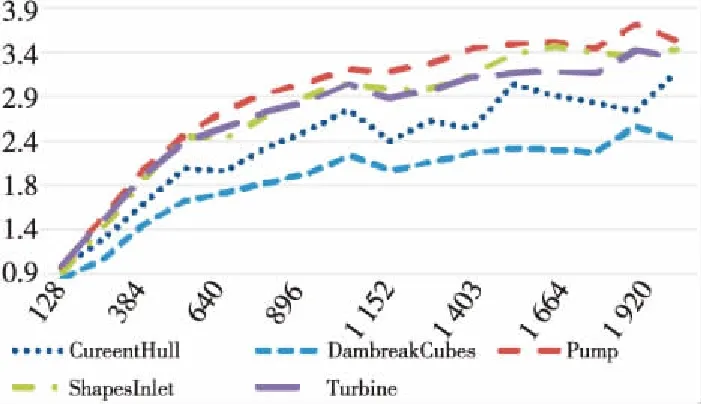
3 // for (int64_ti=0;i 4 //dy[i]=dx[i] *da+dy[i]; 5 // } 6 // } 7 //------------------------------------------------------------- 8 //x0=n,x1=&dy[0],x2=&dx[0],d0=da 9 daxpy: 10 movx3,0//x3=i=0 11 movz0.d,d0//z0=broadcast(da) 12whileltp0.d,xzr,x0//p0=while(0 13 ·L5: 14 ld1dz1.d,p0/z,[x1,x3,lsl 3]//p0?:z1=dy[i] 15 ld1dz2.d,p0/z,[x2,x3,lsl 3]//p0?:z2=dx[i] 16 fmadz1.d,p0/m,z0.d,z2.d/*p0?:z1 +=dx[i]*da*/ 17 st1dz1.d,p0,[x2,x3,lsl 3]//p0?:dy[i]=z1 18 incdx3//i+=(VL/64) 19whileltp0.d,x3,x0//p0=while(i++ 20 b.any.L5// more to do? 21ret 代码中第2~6行显示的是DAXPY运算的源代码,第9~21行显示的是经过编译之后生成的含有SVE指令的汇编代码。记处理器的向量寄存器宽度为VL,1次向量操作最多可处理的数据个数为VL/64。第10行和第11行初始化寄存器x3和z0。第12行的“whilelt”指令对预测寄存器p0初始化,分别对比0,1,…,j,…,VL/64-1和n的大小并为p0的对应位赋值,即p0[j]=j SPH将计算域内的连续介质离散成一系列具有质量、速度和能量的“粒子”,粒子的物理量通过对其支持域内其他粒子进行插值近似,并将函数导数转化为一个核函数的导数,从而实现对Navier-Stokes方程组的离散。粒子随着流体流动并与邻近的粒子产生交互。SPH方法的计算过程被分解成一系列时间步,每一个时间步更新粒子的物理信息,其中最重要的计算过程是粒子间相互作用的计算。粒子间相互作用计算的串行算法如算法1所示。 算法1SPH粒子间相互作用计算串行算法 Procedure ParticlesInteractionSerial Begin 1 // 记P为所有粒子的集合 2foreachp∈Pdo 3q←NeighborCellParticles(p); 4for(i=0;i 5d=distance(p,q[i]); 6if(d 7interact(p,q[i]); 8endfor 9endforeach end 对于计算域P中的任意一个粒子p,首先通过函数NeighborCellParticles获取该粒子邻近单元中所有粒子的列表q,对于列表q中的任意一个粒子q[j],根据p与q[j]的距离d判断q[j]是否在粒子p的支持域内部。若粒子q[j]在粒子p的支持域内(d 函数interact通过如式(1)~式(3)所示的动量方程、连续性方程和状态方程计算粒子间相互作用。 动量方程、连续性方程和状态方程如式(1)~式(3)所示: (1) (2) (3) 在粒子间相互作用计算的串行算法中,内层循环的每一次迭代都需要判断2个粒子之间的距离是否小于支持域的半径,即循环内存在条件分支。条件分支是传统SIMD优化方法的一个难点,而SVE所提供的预测寄存器则能够以类似掩码的形式很好地处理条件分支。 算法2描述了SPH粒子间相互作用计算的SVE向量化算法框架。 算法2SPH粒子间相互作用计算SVE向量化算法 Procedure ParticlesInteractionSVE Begin 1 // 记P为所有粒子的集合 2foreachp∈Pdo 3q←NeighborCellParticles(p); 4for(i=0;i 5pd0=svwhilelt(i,len(q)); 6vq[0:n-1]=ld(pd0,q[i]); 7vd[0:n-1]=distance(pd0,p,vq[0:n-1]); 8pd1=svcmplt(pd0,vd,h); 9interactSVE(pd1,p,vq[0:n-1]); 10endfor 11endforeach end 如第4行所示,循环的每一次迭代最多处理n个粒子,n的计算方法为向量寄存器的宽度除以单个数据的大小(假如向量寄存器宽度为128位,数据类型为双精度浮点,即一个数据的大小为64位,则n=128/64=2)。第5行通过循环控制变量j和列表q的长度len(q)构造预测寄存器pd0,预测寄存器pd0包含n个元素,pd0[k]=(j+k) 观察粒子间相互作用计算的3个方程,动量方程和连续性方程均涉及大量的求和运算,占据了粒子间相互作用的绝大部分计算时间,而且2个方程中存在大量的数据级并行,因此,下面将重点描述如何采用SVE对动量方程和连续性方程进行向量化。以下的向量化并行计算均在预测寄存器的控制下进行。 动量方程是关于粒子速度矢量vk的方程,包含x,y,z3个方向的分量,各对应一个方程,如式(4)~式(6)所示: (4) (5) (6) Figure 2 SIMD calculation of 动量方程右侧的第2部分比第1部分更为复杂,将分3步描述第2部分的向量化计算方法。首先在图3中描述了rij·vij的计算过程,其中,rij·vij=rij|x×vij|x+rij|y×vij|y+rij|z×vij|z,图3中记rvij=rij·vij。注意图3中(rvij0|x,rvij1|y,…,rvijn-1|y),(rvij0|z,rvij1|z,…,rvijn-1|z)与(rvij0|x,rvij1|x,…,rvijn-1|x)的计算过程类似,故省去。在图3中,ri|x和vi|x通过标量取获得,(rj0|x,rj1|x,…,rjn-1|x)和(vj0|x,vj1|x,…,vjn-1|x)通过向量取获得,图3中的计算全部为向量运算。 Figure 3 SIMD calculation of rij·vij Figure 4 SIMD calculation of 记: Figure 5 SIMD calculation of Figure 6 SIMD calculation of wij 本节对本文所提出的向量化方法的加速效果进行评估。本文采用5个测试用例,分单精度和双精度2种模式,对比了从128位~2 048位共16种向量寄存器宽度情况下粒子间相互作用向量化算法对串行算法的加速比,得到了单精度和双精度2种模式下最高3.71倍和4.92倍的加速比。 (1)模拟器。本文采用了ARM指令模拟器ARMIE(ARM Instruction Emulator)对SVE指令开展模拟。ARMIE是ARM公司为了方便相关从业人员进行SVE指令的研究而推出的一个模拟器,ARMIE可以通过选项“-msve-vector-bits”指定模拟的向量寄存器宽度,支持从128位~2 048位共16种不同的向量寄存器宽度。受模拟器运行速度的限制,对测试用例完整计算过程的模拟难以在有限时间内完成,因此后续实验针对每一个测试用例选取了计算过程中的部分时间迭代开展模拟。 (2)软硬件平台。ARMIE需要运行在支持ARM AArch64指令集的硬件平台上。实验所采用的是一个FT-2000+/64[15]的CPU,包含64个核,64 GB主存,实验使用的编译器为GCC-10.1.0,为了生成SVE指令,给编译器提供的编译选项为“-O2-march=armv8-a+sve”。 (3)SPH软件平台。本文选择开源SPH项目DualSPHysics[16]作为本实验的软件平台。DualSPHysics由西班牙维戈大学和英国曼彻斯特大学共同开发,采用C++语言编写,适用于剧烈运动或重力场和液体的建模场景。本文对DualSPHysics项目中计算粒子间相互作用的部分进行了向量优化,粒子间相互作用的计算占据了DualSPHysics计算过程的大部分时间。对于粒子间相互作用的加速可以显著提高整个软件的性能。 (4)测试用例。实验采用5个测试用例来验证向量化的加速效果,对测试用例的简要描述以及测试用例的规模(粒子数量)如表1所示。 对于上述5个测试用例,本文采用了2种不同的精度模式:单精度和双精度,对比了从128位~2 048位16种不同向量寄存器宽度的情况下,粒子间相互作用计算部分,经过SVE向量化之后对比非向量化的加速比。 Table 1 Description of the testcases 单精度和双精度2种不同模式下的加速比如图7和图8所示。可以看出双精度模式下的加速比要高于单精度模式下的加速比。单精度模式和双精度模式下的最高加速比来自于测试用例Pump,分别为3.71倍和4.92倍。加速效果与ARM针对其他Benchmark所给出的最高加速比存在差距的原因主要包括2个方面:一方面是因为粒子间相互作用的计算仍然存在串行计算部分,并不是所有的计算都可以通过向量化并行计算,比如由于粒子的位置发生了变化,需要更新粒子所在单元的信息;另外一方面,在算法2的SVE向量化算法中,第4行所遍历的粒子均需在第7行计算其与粒子的距离,只有距离小于支持域半径的粒子才会参与后续的向量运算,向量寄存器并没有被填满,这也是SVE的特点之一。 Figure 7 Speedup in single precision mode Figure 8 Speedup in double precision mode 为了验证SVE向量化算法的正确性,本文以测试用例DamBreakCubes为例,对比了非向量化算法的渲染结果与SVE向量化算法的粒子分布,结果如图9和图10所示。通过对比可以发现,经过SVE向量化加速之后的粒子分布与原始结果的渲染图一致,表明本文所提出的SVE向量化方法是正确的。 Figure 9 Rendering effect of the testcase DamBreakCubes using serial algorithm Figure 10 Particle distribution of the testcase CamBreakCubes using SVE algorithm 本文基于ARM SVE扩展指令集对光滑粒子流体动力学(SPH)开展了SIMD优化,对SPH计算过程中的粒子间相互作用计算进行了向量化并行,在单精度模式下取得了最高3.71倍的加速比,双精度模式下取得了4.92倍的加速比。下一步将开展大规模SPH计算在SVE硬件平台上的加速效果研究。3 SVE向量化优化方法
3.1 SPH粒子间相互作用向量化并行计算框架
3.2 动量方程向量化

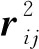
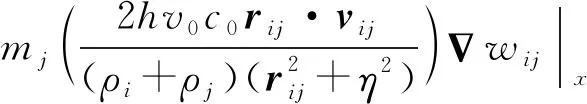
3.3 连续性方程向量化
4 实验结果


5 结束语
