基于设计结构矩阵的航天项目解耦方法研究——以载人航天工程项目Z为例

■ 章朝奔 张善从

1.中国科学院大学经管学院 北京 100190

2.中国科学院空间应用工程与技术中心 北京 100094

0 引言

近年来,我国对航天项目研制需求迫切，型号研制呈井喷式发展,高密度发射将常态化。多型号研制与高密度发射对航天项目进度有很强的刚性要求,传统的型号研制管理模式已不能满足当下快速发展的需要。[1]就目前多数承接航天工程项目单位的实际状况而言,项目进度严重滞后，成本远超预估的现象频繁发生，产生此类问题的根源就在于缺乏有效的管理方法。项目管理人员在制定项目进度计划时，因不能较好识别和处理好任务间耦合情况,使得任务在执行过程中存在大量的反馈返工现象,严重影响研制效率。[2]因此研究新的管理方法来为降低航天项目总体耦合度成为迫切要解决的问题。

设计结构矩阵（Design Structure Matrix,DSM）作为项目管理任务排序的数字建模方法，具有较强的表达任务关系，提供直观分析的优点，在国内外部分项目管理领域里得到的应用。Rosnani Ginting 等[3]指出设计结构矩阵具有直观表述项目任务关系，方便项目管理里人员进行优化的特点。麻省理工大学的Eppinger Steven D,Browning Tyson R[4]对设计结构矩阵的概念及应用场景开展了论述，设计结构矩阵能够较好运用于产品开发进度优化。Toufik Boudouh 等[5]通过文献综述，提出利用设计结构矩阵对项目任务重新排序可以有效减少任务反馈的数量。李艳[6]通过研究设计结构矩阵成功对产品开发的进度进行改善。杨青等[7]进一步证实了设计结构矩阵在复杂研发项目建模与优化研究的可行性。杨宝森等[8]基于设计结构矩阵建立了关系模型，迭代模型，重叠模型，上下游约束，层次模型五种模型用以描述项目任务关系。辛君捷[9]利用设计结构矩阵对航空武器装备复杂研制过程的耦合度较高的任务进行识别，提出对应的改进措施减少高耦合度任务对项目进度的影响。罗新星[10]首次在软件开发项目上使用设计机构矩阵优化项目流程，进一步拓宽了设计结构矩阵应用场景。陈庭贵,琚春华[11]提出将反馈数量较大任务转为流程上游任务，实现任务信息传递由反馈转为前馈，降低了流程反馈带来的迭代返工次数的项目任务解耦方法。

从上述的研究可知，学者们对耦合度的计算与降低耦合度的研究相对较少。有关研究所提出的任务反馈数量最少的优化方法实际效果与理论效果存在一定的差距。本文基于设计结构矩阵，构建项目耦合度函数，提出一种利用遗传算法寻找较少的任务反馈和任务耦合的排序来降低项目总体耦合度的方法，并与任务反馈数量最少的解耦方法做出比较。

1 项目管理任务关系优化方法

1.1 任务关系建模

Donald Steward在1981年引入设计结构矩阵来分析信息流，它是一个n阶方阵，用于显示矩阵中的各个元素的交互关系，有利于对复杂项目进行可视化分析。[12]

制定项目流程首先需对项目进行分解，将项目拆分为一个个独立的，可操作的任务，该过程被称作项目任务分解。[13]在项目任务层面,项目管理人员对项目内任务的关系进行判断，建立设计结构矩阵，确定任务间的信息前馈反馈关系。

若将某项目分解为n 项子任务(t1,t2,···,tn)，其子项目构成n阶设计结构矩阵Aij方阵：

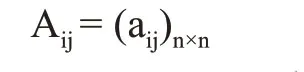
在设计结构矩阵中，aij=1 定义任务间发生了信息传递。若i ＞j 表示矩阵下三角区任务i 对任务j 产生信息前馈；若i ＜j 表示矩阵上三角区任务i对任务j产生信息反馈。[14]项目中任务信息反馈往往造成局部的迭代返工现象，若i 与j 相差值较大，表明任务信息反馈传递距离较远，需要迭代返工的任务数量较多。

通过设计结构矩阵，可将项目任务间存在的串行、并行以及耦合3种任务关系转化为矩阵形式。[15]相较项目流程图，设计结构矩阵能够更加直观表现任务繁多复杂、耦合度高的项目。项目任务关系与设计结构矩阵赋值对应关系见表1。

表1 任务关系转化为设计结构矩阵

将任务关系通过设计结构矩阵表达后，对反馈数量较多的任务执行顺序进行调整，降低项目总体耦合度[16]调整项目所分解的任务的顺序，如图1(a)所示，任务F 不依赖其他任务的输入，只有对任务C 与任务E 的反馈。将任务F的顺序从末位调至首位，图1(c)为调整任务F后的设计结构矩阵，矩阵上三角的非零数减少，项目表现为任务F对任务C与任务E的反馈转为前馈。

图1 设计结构矩阵任务调序

1.2 项目任务优化

一般地，为了避免过多任务反馈所带来的进度风险，需经过多次任务顺序调换，使得设计结构矩阵满足式(1)中任务反馈总数Fb值最低的条件[17]。

Fb值反应了项目任务反馈总数，单以项目任务反馈总数进行流程寻优，可能获得多个对应的项目任务排序不同解，其所对应的项目任务关系不同，部分排序存在任务反馈总数低但任务反馈回路跨度较大的排序，大反馈回路任务无法避免路径上多项任务迭代返工的传递，降低了项目解耦优化效果。

结合项目管理实际，在任务反馈总数较少但任务反馈跨度较大的情况下，项目依然存着较大数量的任务迭代返工情况，项目任务耦合程度不仅与任务总反馈数相关，更与任务反馈的前序任务与任务反馈任务数量之比及任务反馈跨度相关[18]，构建式（2）任务耦合程度函数Fc：

当项目任务量较大，n 项任务需要进行n!比对，无法通过简单的任务调序与手动计算获得最优解为了使得设计结构矩阵更具实用性，通过引入智能算法对设计结构矩阵的排序最优值进行求解，以获得项目总体任务最低耦合度的最优任务排序。

2 智能寻优算法

遗传算法（Genetic Algorithm,GA）[19]是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，不需要确定的规则就能自动获取和指导优化的搜索空间，自适应地调整搜索方向。遗传算法以一种群体中的所有个体为对象，并利用随机化技术指导对一个被编码的参数空间进行高效搜索。

遗传算法基本实现流程如图2所示：

图2 遗传算法基本流程

因此，利用遗传算法可将排序寻优问题转化为获得满足适应度函数最大值的种群，其种群染色体对应设计结构矩阵任务排序即为项目任务最优排序。

2.1 染色体交叉变异原则

采用任务编码方式，在一个具有n项任务的项目中，可通过任务关系建模，获得n阶设计结构矩阵，将任务由1至n非重复构成n位染色体，通过初始种群生成随机顺序染色体，经过遗传选择交叉变异生成子群的方式来进行改变任务顺序的项目总体任务耦合度计算，交叉变异规则如图3所示。每一类子群所携带染色体对应一种设计结构矩阵任务排序，对子代种群进行交叉变异处理替换父群中低适应度的个体，使得每代种群的适应度不低于上一代种群，直至获得最高适应度的子群。[20]

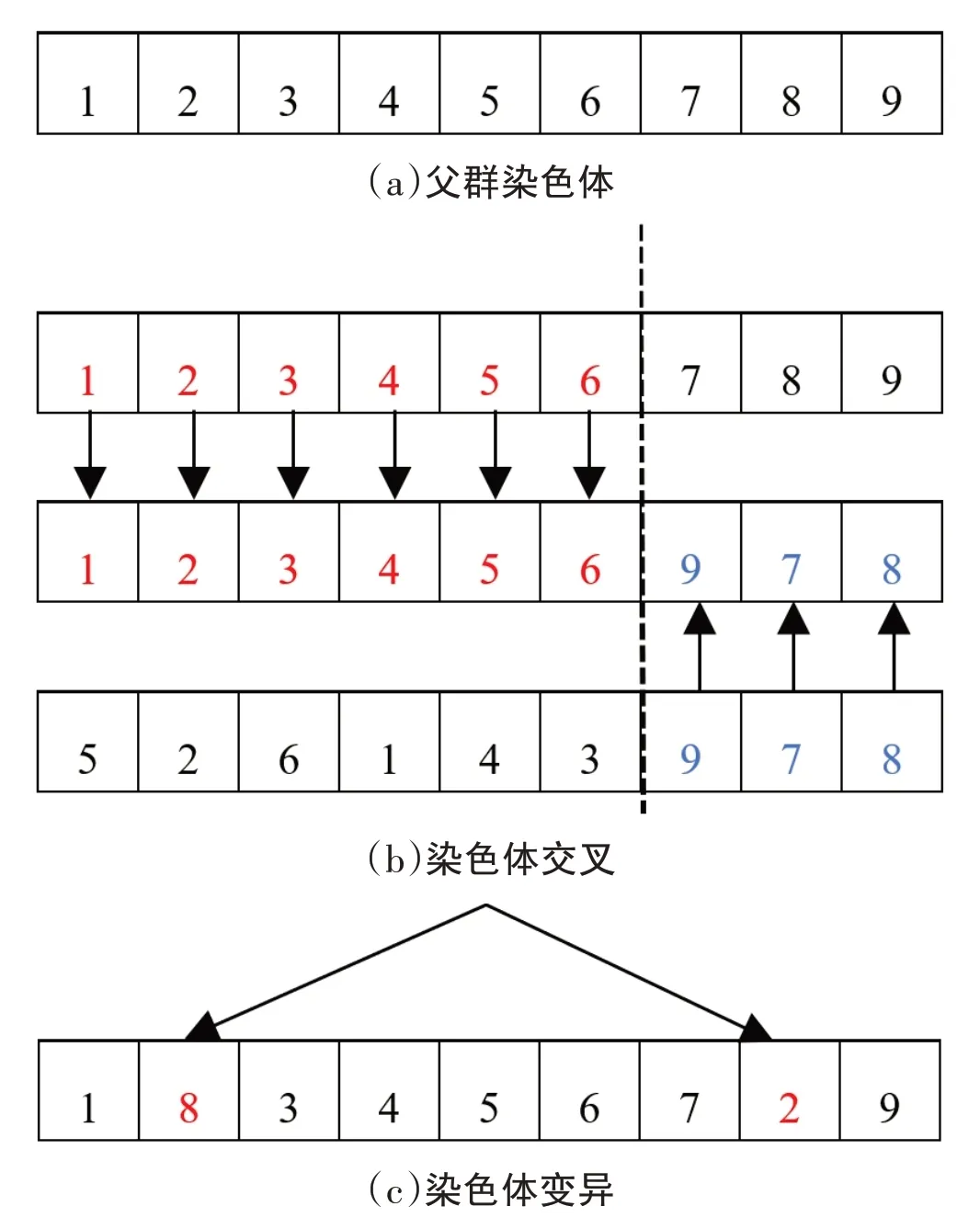
图3 染色体交叉、变异规则

子代染色体交叉与变异需满足如下规则：父群适应度函数值较大者，可以保持较为完整的染色体长度。染色体变异概率视种群染色体长度而定。

2.2 适应度函数构建

遗传算法适应度是种群对环境的适应程度的表现，适应度函数值越大，表现为种群对环境适应度越高，在设计结构矩阵任务排序中，表现其排序任务间耦合度较低。

将设计结构矩阵的行i与列j作为变量，通过遗传算法进行寻优，求得最优任务安排计划。定义适应度函数Fs：1

其适应度函数表现形状为，个体染色体序列所对应的项目任务总体耦合度较大，其适应度函数值较小，通过遗传算法寻优适应度函数值最大者即为项目任务总体耦合最小者。

2.3 遗传算子选择方法与遗传算法终结

算子选择策略为轮盘赌选择策略，即子群将染色体传入下代种群的概率为该子群的适应度呈正比，适应度大的个体将染色体传入下代，以实现整个种群的适应度保持优化。

算子交叉规则为适应度比值法，如式(4)R 值表示子群保留父群染色体比例为父群1 与父群2 的各自适应度与二者适应度总和之比，适应度高的父群获得染色体保留比例高，当父群1 与父群2 保留的染色体上的数发生重复时，对保留染色体比例少的父群从前至后检索未重复数字补足染色体。

算子变异规则为随机点交换，若染色体长度为n时，随机选择i,j两点且i ＜j ＜n。i，j为染色体第i位与第j位基因值，将二者位置对调后视作染色体变异，以概率Cm值对染色体进行变异作为子群，替换被淘汰的适应度较低的个体。

算法终结策略为适应度函数值达到最大保持多无变化或者子群代数已经达到所设置的最大值位置。

3 应用实例研究

本文以载人航天工程Z项目为实证研究案例。项目描述：该项目为试验载荷提供满足非牛顿引力实验项目要求的超高微重力环境水平，加速度计为实验传输重力参数；工程电子学设计保证有效载荷供电与元器件运行环境，避免电磁干扰带来的数据记录影响；结构热工艺设计确保有效载荷在执行空间任务时面对复杂的空间环境有着较好的适应性；工装设计保证产品运输损坏，涉及较多产品接口匹配问题；地检设备模拟各项零部件，测试系统接口统一性；结构件为该装置提供机械支撑；六性设计确保该装置在空间环境下正常工作；核心部组件设计确保其功能实现。承研项目重要性高。

Z项目主要由8个任务构成如图4所示，项目具体的所含任务为加速度计设计、工程电子学设计、工装设计、结构热工艺设计、地检设备设计、结构件设计、六性详细设计、核心部组件设计。为了通过设计结构矩阵表达任务间关系，将项目Z的8项任务由A至H编号。

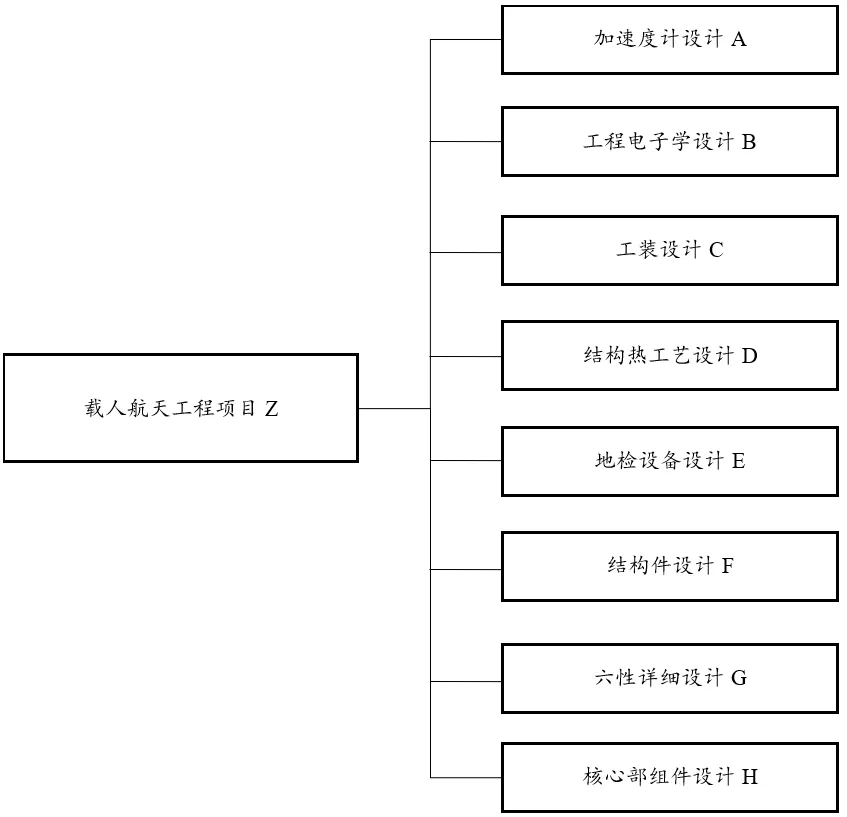
图4 载人航天工程项目Z任务分解

选择该项目的原因如下：代表性。Z 项目严格按照载人航天工程项目顶层规范执行，其项目管理模式，项目研制流程编制具有载人航天工程项目的代表性，该项目优化所得的结论也适用于其他系统载人航天项目；典型性。Z项目包含六性设计、工装设计、电子学设计以及地检设计，与各承研单位项目有着较多近似任务。该项目包含良好的实验环境，方便获取更优良的项目数据，可作为载人航天工程项目管理方法应用实践的典型代表。

3.1 初始设计结构矩阵

项目管理人员通过专家调查法结合德尔菲法，充分了解项目任务之间的前馈与反馈关系后，用摩尔值表达任务间的串行、并行及耦合关系，获得载人航天工程项目Z初始任务设计结构矩阵。载人航天工程项目Z设计结构矩阵如图5所示。

图5 项目Z初始设计结构矩阵

在项目Z中，任务G六性详细设计，需要给工程电子学设计，工装设计，结构热工艺设计、地检设计进行提供详细参数与接口标准；同时工装设计，结构热工艺设计需要来自工程电子学设计的信息输入。整个项目流程中，矩阵上三角任务反馈总数为9，且存在着3 个超过总任务数量半数的大反馈回路与3个多任务反馈回路。由此可见，项目Z 初始设计结构所表示的项目流程耦合度较高。

3.2 遗传算法寻优

在该项目中，8 个任务共存在40320 种任务排序可能。通过python 编程，导入图5 项目Z 初始设计结构矩阵，结合遗传算法对设计结构矩阵任务排序进行寻优，具体参数设计如下，群体规模T 为100，种群交叉概率0.7，种群变异概率0.3，终结条件为进化200代数。

适应度是个体对环境的适应程度的表现，适应度函数值越大，表现为个体对环境适应度越高，在设计结构矩阵任务排序中，其表现形式为排序任务间耦合度较低。将8项任务生成初始种群后，进行遗传选择，交叉与变异，交叉方式为式(4)值，比对适应度函数式(3)大小，进化200代后种群后输出优化后设计结构矩阵。

经过遗传算法寻优后得图6 任务排序的设计结构矩阵。

图6 优化设计结构矩阵

优化后的设计结构输出任务顺序为六性详细设计、加速度计设计、结构热工艺设计、工程电子学设计、结构件设计、核心部组件设计、工装设计、地检设备设计。设计结构矩阵右上方的反馈任务数量减少，只存在AD 两项耦合任务，项目整体任务耦合度较低。

项目任务实际来看，六性详细设计任务靠后往往会导致构热工艺设计、工程电子学设计及工装设计、地检设备返工，提前制定详细六性设计可以有效避免四项任务的返工，减少任务间信息协调时间。加速度计设计需要接收来自结构热工艺设计及工程电子学设计的反馈，加速度计设计与结构热工艺设计及工程电子学设计任务间涉及接口匹配问题与电子学参数问题，在实际工作中可以将结构热工艺设计及工程电子学设计两项任务并行执行，并保证两项任务能及时给加速度计设计的信息反馈，避免产生工程短线。

3.3 项目任务优化效果计算

执行遗传算法获得最终项目设计结构矩阵，需要对项目任务优化效果进行对比计算。为比较最少任务反馈数优化与最低耦合度优化效果，对该项目做最少任务反馈数优化的设计结构矩阵如图7所示。

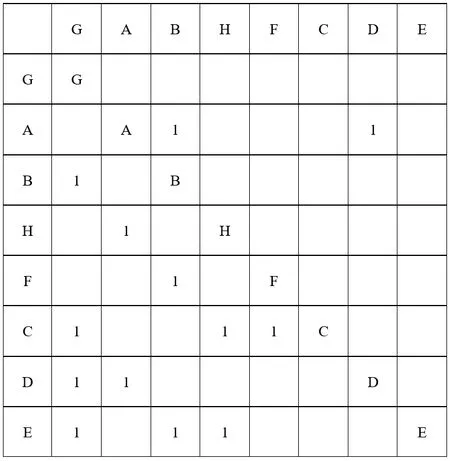
图7 最少任务反馈数优化

根据式1与式2，可以分别计算出最少任务反馈数排序与最低耦合度任务排序载人航天工程项目Z任务优化前后的任务反馈总数与任务总体耦合度，表2 为项目设计结构矩阵优化前后对比数据。

表2 项目设计结构矩阵优化前后对比

载人航天工程项目Z的初始设计结构矩阵通过遗传算法寻优后，其输出结果的矩阵中任务反馈总数降低了7，任务反馈总数为优化前的0.22。任务耦合度值比优化前减少了92.2%，项目中大任务反馈回路消失，多任务反馈回路，多任务耦合优化为任务间数量较多的大反馈回路变为数量为1 和任务跨度为1 的小回路。相较最少任务反馈数排序，项目任务耦合度得到进一步降低，从而有效地避免了频繁的任务反馈和任务耦合导致任务重复而造成项目进度滞后的问题。

4 结论

本文针对航天工程项目复杂，内部迭代繁多，任务耦合严重，现行项目管理方法难以直观表达项目任务关系，对项目任务进行解耦优化的问题，提出如下解决方法：

（1）利用设计结构矩阵将任务流程通过矩阵表达，矩阵上三角区反映项目任务总体反馈情况，项目管理人员可通过设计结构矩阵对反馈数量较多的任务进行识别。

（2）改进项目任务排序寻优目标函数，构建基于反馈长度与反馈影响程度的项目任务耦合度评价函数对原有设计结构矩阵排序存在的上三角的任务反馈数量多，项目任务耦合度较高的问题进行优化。

（3）通过遗传算法解决设计结构矩阵任务流程排序寻优计算问题。构建寻求项目总体任务耦合度最低的目标函数，结合载人航天工程项目Z 案例实证。结果表明，求解输出后的设计结构矩阵任务反馈的大回路反馈数明显减少，项目任务总体耦合度得到了降低，避免了工程短线发生。