基于子空间划分和自我表示学习的高光谱波段选择
2021-06-24汪国强
王 鑫, 汪国强
(黑龙江大学 电子工程学院, 哈尔滨 150080)
0 引 言
高光谱图像(Hyperspectral image, HSI)通过大而窄的电磁波波段获取感兴趣目标的信息。与-RGB图像相比,这些波段能够提供更加丰富的光谱和图像信息,可以更好地描述目标的光谱特征,提高检测和识别能力。因此,它被广泛应用于各种研究领域,如海洋勘探、军事目标探测、林业、医学影像处理和生产质量检验等[1]。这些波段为相关图像处理提供了更多的信息,但也带来了一些障碍,根据高光谱成像特征,相邻光谱波段之间存在较高的相关性。高维HSI数据处理不仅增加了时间复杂度和空间复杂度,而且会出现维数休斯现象,导致分类性能的恶化[2]。同时,高光谱数据的高维性使得数据的传输、存储和处理面临着一系列困难。因此,降维技术成为HSI分析中一个备受关注的问题。
降维技术通常可以分为特征提取和特征选择(波段选择)两类。特征提取是根据一定的准则将高维空间数据映射到低维空间,提取新的特征子集来表示原始的高光谱数据。典型的方法有主成分分析(Principal component analysis, PCA)[3]、线性判别分析(Linear discriminant analysis, LDA)和独立成分分析(Independent component analysis, ICA)。但通过空间变换,会改变原始高光谱数据的物理意义,丢失一些关键信息。而特征选择也称为波段选择,是从原始光谱波段集合中选择波段子集,可以最大化数据分析的性能。波段选择方法可能只需要一个选定的光谱波段子集来进行后续数据分析。与特征提取方法相比,波段选择能够更好地保存物理信息,对原始数据具有更好的解释和表达能力。
根据标记样本是否被利用,波段选择可以分为监督、半监督和无监督方法。监督和半监督方法在很大程度上依赖于监督信息来识别相关波段。这些方法由于标签信息允许评估类的可分离性,最终只选择具有强识别性信息的波段。显然,这些方法更加以分类为导向,有利于取得更好的分类性能。然而,由于HSI数据总是难以标记,这两种方法在应用中并不十分实用。无监督方法只需要通过一些评价准则函数从高光谱波段中选择一个子集,不需要使用标记样本。常用的判定标准有方差、信噪比、熵、k阶统计量和欧氏距离等[4]。基于该策略,现有的无监督波段选择方法主要可以分为基于排序、搜索、聚类、稀疏、嵌入学习和混合模式的方法。这些波段选择方法虽然都能取得令人满意的分类结果,但在分类过程中存在两个固有的缺点。一方面,大部分只考虑波段之间的相关性,忽略了所选取波段的信息量,并不符合波段选择的原则[5]。另一方面,对于某一波段,在一定范围内与相邻波段的相关性较强,与更远波段的相关性较低。因此,可以得出不同波长范围的不连续波段不能分组成簇进行波段选择的结论。
大数据分析的一个可行方案是将大数据集拆分为多个较小的数据集,使用合适的算法或模型依次对每个小数据集进行处理。这些场景要求波段选择模型能够处理来自不同时间的不完整波段的动态数据,捕捉这些数据之间的某种一致性[6]。针对以上问题,可将高光谱图像立方体划分为若干子立方体,并在子立方体中选择信息波段。本文采用了一种自适应子空间划分策略来划分立方体,通过自表示学习逐一处理子立方体,采用记忆向量来处理缺失波段,可指导后续的波段选择。
1 算法描述
首先,采用自适应子空间策略对高光谱图像立方体进行划分,基本思想是有序地处理高光谱波段,然后自适应地将具有相似光谱特征的波段划分为一个子立方体。再采用自表示学习算法去处理子立方体,在处理完所有子立方体以后,采用记忆向量q进行波段选择。
1.1 自适应子空间划分策略
考虑到相邻波段的相关性高于非相邻波段,采用自适应子空间划分策略对高光谱图像进行立方体分割,可以使用聚类算法来实现空间划分。但是,如果直接采用聚类算法,会导致更大的时间复杂度。为了更快地分割高光谱图像立方体,该方法采用了粗精细策略,主要有两个步骤:
(1) 粗子空间划分
设X∈RW×H×L表示高光谱像立方体,其中L为总的波段数,W和H分别为每个波段的宽度和高度。波段选择的目的之一是减少计算时间。因此,为了更快地实现聚类算法,将高光谱图像立方体按照选择的波段数等宽分成有限的子立方体,每个子立方Pi的带数定义为:
(1)
式中K为所波段的数目。这种方法是一个初始划分,可以得到子立方体Pi∈RW×H×X。
(2) 细子空间划分
为了准确表示每个子立方体Pi的光谱波段,提出了一种细子空间划分方法来获得新的子立方体。其中,每个空间波段的矩阵被拉伸成一维向量:
X=[x1,x2,…,xL]
(2)
式中xi∈RW×H×1,xi是第i个波段的拉伸向量。
根据拉伸的波段向量,利用欧几里得距离构造第i个波段和第j个波段之间的相似矩阵为:
(3)
在聚类算法中,常利用类内和类间距离来分析问题。具体来说,通过最大化类间距离与类内距离之比来获得最终的聚类结果。对于已分割的高光谱图像立方体,利用这一思想对该立方体进行了精确的分割。由于两个相距很远的子立方体之间的相关性很小,故只考虑两个相邻子立方体Pi和Pi+1之间的关系。因此,给出目标函数的一般形式为:
(4)
式中:Dinter和Dintra分别为类间距离和类内距离;t为划分点。
在类间距离的计算中,选择最大距离作为衡量两个类间关系的标准,它被定义为:
Dinter=max|Dij|
(5)
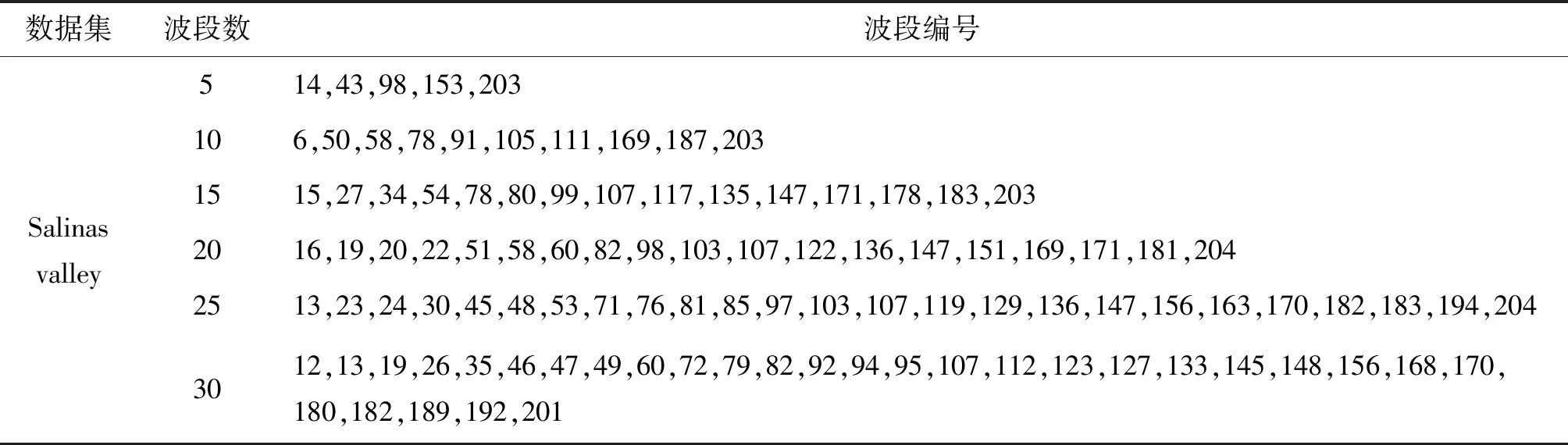
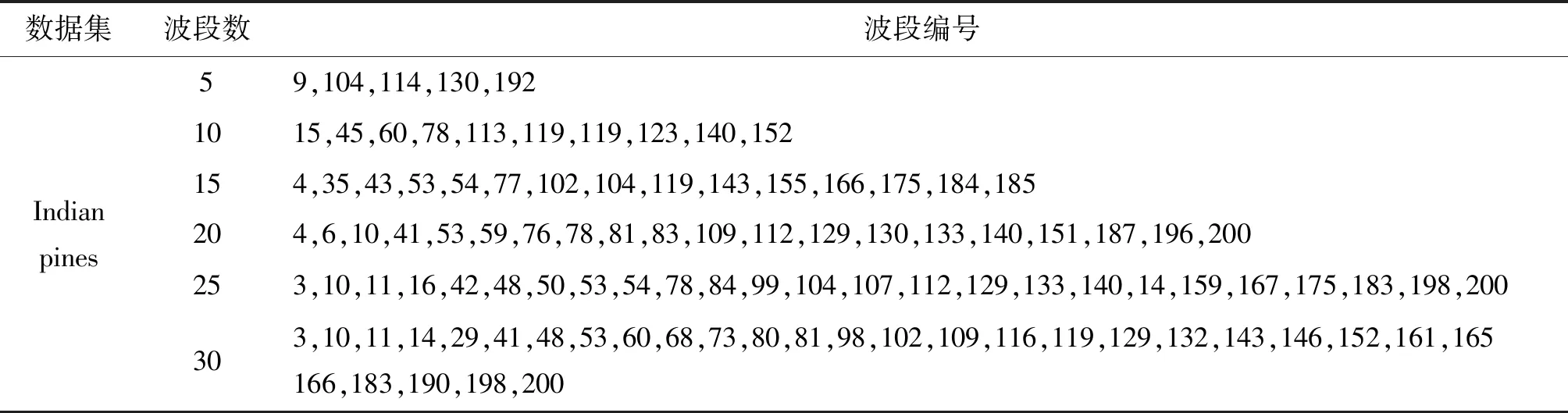
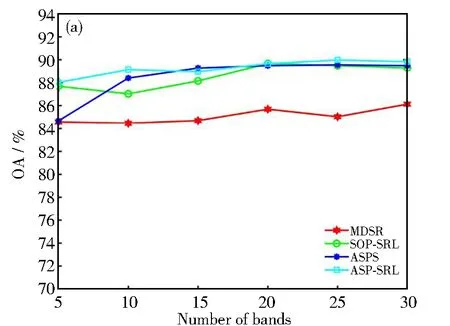
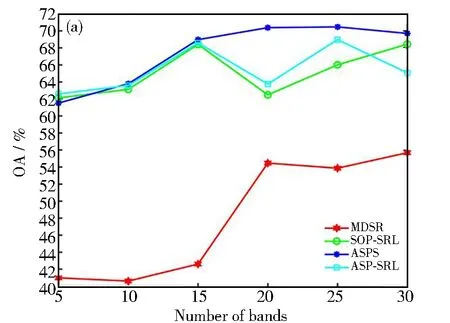
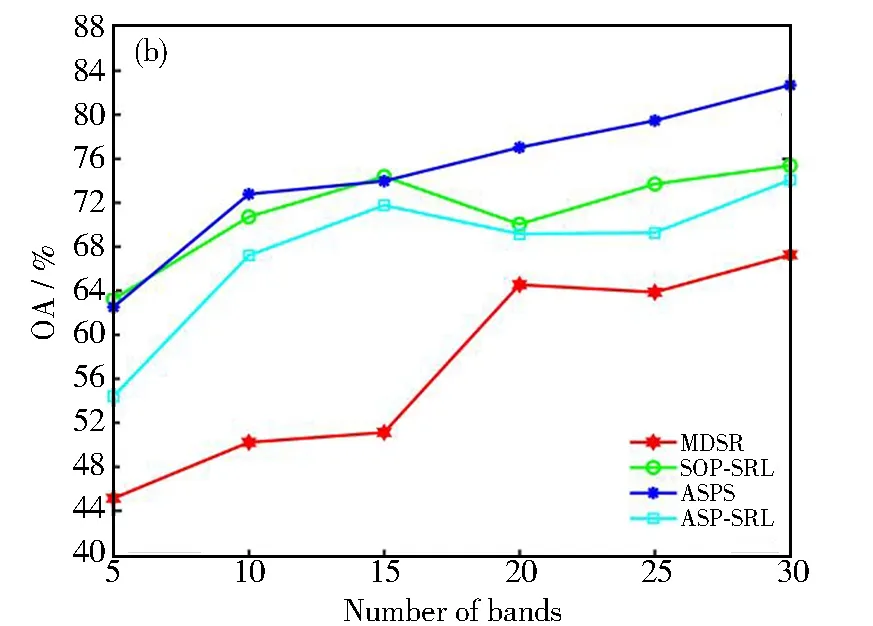
式中1≤i Dintra=U1+U2 (6) 式中: (7) (8) 由上述方程得到第一个精确划分点,而不是原来的划分点。因此,利用之前的划分点,以同样的方式更新初始点t,得到最终的分割点,如图1所示。示例将高光谱图像立方体(8个波段)划分为4个子立方体。在虚线内,深色区域表示仅考虑这些相邻的波段来更新当前的分割点。这种划分方法可以使得到的子立方体之间的相关性降低,有效地避免选择冗余波段,符合波段选择原则。 图1 自适应子空间划分原理示意图 由于冗余波段的自表示性质,对于给定的样本矩阵X,SRL将每个波段表示为其他波段(包括自己)的线性组合,建模如下: XT=XTW+E (9) 式中:变量W∈Rb×b和E∈Rn×b分别表示系数矩阵和残差矩阵;b表示样本总的波段数;n表示总的样本数。矩阵E的第i行表示训练样本Xi的重构误差。为了避免在模型(9)中获得平凡解(即W=I和E=0),必须对W进行正则化。因此,SRL的正式定义为: (10) 在式(10)中,第一项是一个损失函数,如最小二乘或平方损失函数,以最小化重构误差。第二项是一个正则化项,是为了避免平凡解和指导波段的选择,低秩约束和行稀疏约束是两种常见的正则化项。通过交叉验证确定的正参数τ用于实现第一项和第二项之间的平衡。 波段选择可以使用损失函数和正则项的各种组合来实现。与平方损失函数相比,最小平方损失函数对异常值具有鲁棒性。此外,当增加主要波段之间关系的低秩约束时,有必要进行额外的聚类,这增加了计算复杂性,并使相应的波段选择模型陷入困境。因此,具有由最小二乘损失函数和行稀疏约束组成的自动波段选择的鲁棒自表示模型为: (11) ‖W‖2,1理论上可以使矩阵W的某些行的值变为零。‖Wi‖2=0表示在重建过程中第i个波段被舍弃了。相反,‖Wi‖2的值越大,意味着选择第i个波段的可能性就越大。因此,‖Wi‖2可以被认为是第i波段的分数。在求解变量W之后,自表示模型选择得分较高的波段。式(11)可以用收敛的迭代加权算法来求解[7]。 1.2.1 记忆向量 基于这样的一个假设,即波段的重要性是连续的,如果一个波段是重要的,那么它在不同时间的样本矩阵中也是同等重要的。为了方便起见,假设记忆向量q在一次处理样本之前记录了大量的历史波段。因此,使用一个记忆向量q∈Rb来记录所有波段的分数。元素的值越大,选择相应波段的概率越大。当一个样本矩阵Xt∈Rbt×nt在t时刻具有不完全波段时,首先,从对应于Xt的可用波段的记忆向量q中得到子向量qt∈Rbt。然后,利用行稀疏约束的SRL来获得Xt对应的系数矩阵Wt。随后,使用矩阵Wt来更新记忆向量q中Xt的可用波段的分数。当在时间t+1的样本矩阵Xt+1可用时,重复以上过程。最后,所有可用的样本矩阵扫描一次后,用q向量进行波段选择。 基于上述波段重要性连续的假设,使用一种正则化项来利用历史信息优化矩阵Wt为: (12) (13) 式中:τ1和τ2是正参数,用来保持第一项和第二项之间的平衡;Vt是取决于重构误差的权重向量;r是用于调整权重分布的参数。 采用矩阵Wt行的l2范数来更新向量q中对应于Xt可用波段的元素的值。这样,在记忆向量中记录了样本矩阵Xt所反映的波段的分数。当t+1时刻的样本矩阵Xt+1可用时,重用更新后的记忆向量的式(13)。根据q的元素以降序对所有波段进行排序,选择排名靠前的波段。 为验证本文方法的可行性与有效性,与基于可扩展单程自表示学习高光谱波段选择(SOP-SRL)[8]、基于自适应子空间划分策略的高光谱波段选择(ASPS)[9]和基于多字典稀疏表示的高光谱图像无监督波段选择(Multi-dictionary sparse representation,MDSR)[10]进行了对比。 实验环境为第十代智能英特尔六核处理器,主频2.60 Hz,内存16 GB,开发环境为Matlab R 2016 a。实验数据为萨利纳斯山谷(Salinas valley)、帕维亚大学(Pavia university)和印第安农场(Indian pines)三个公开的高光谱遥感影像数据集。三组数据所对应的地物类型及数目如表1所示。 (1) 萨利纳斯山谷数据。该数据共有512×217个像素,以3.7 m的空间分辨率拍摄于美国加利福尼亚的萨利纳斯山谷。显示了不同种类的植被,对应于16类地物。原始数据包含224个波段,但是由于大气吸收或噪声污染,删除了20个波段,剩余204个波段。 (2) 帕维亚大学数据。该数据的波长范围为0.43~0.86 μm,空间分辨率为1.3 m,共有610×340个像素点,共包含9类地物。该数据集共包含115个波段,删除了12个噪声波段,最后剩余103个波段。 (3) 印第安农场数据。此高光谱数据是在1992年,采用AVIRIS传感器拍摄的印第安纳州西北部农业区影像,像素大小为145×145,共220个波段,包括16类地物类别。去除吸水严重和低信噪比的20个波段,最后剩余200个波段。 表1 三个数据集地物类别及数目表 采用K近邻(K-nearest neighbor,KNN)、(Support vector machine)SVM分类进行实验。KNN是机器学习中最简单的分类器,它根据K个相似训练数据的类别确定样本类别。通过交叉验证来选取最优的K值,因此,最终选定K值为5。SVM分类器采用RBF核。另外,考虑到分类器是被监督的,因此,从每个类别中随机抽取10%的样本作为训练集,其余90%的样品用于测试集。为了减少随机选取10%样本的影响,算法运行10次以获得平均结果。因为所选取波段的数目未知,所以本次实验在5~30个波段内进行试验,以此验证波段数对分类精度的影响。对于分类的结果采用总体准确率(Overall accuracy, OA)、平均准确率(Average accuracy, AA)和Kappa系数作为高光谱图像分类评价指标。OA和Kappa值越大,说明图像分类效果越好,AA是评价小类别分类结果好坏的常用指标。 首先,对萨利纳斯山谷数据和帕维亚大学数据进行了子空间划分,于每个子空间内各选择一个波段,获得相关性较低的波段组合,假如选择5个子空间,那么他们分别为(1~38)、(39~62)、(63~104)、(105~202)和(203~204)。从这5个子空间中按照前面方法各取出一个相关性低且信息量大的波段进行组合,然后送入到分类器中进行分类。不同波段数在三个数据集上的分类性能指标如图2所示,为了更好地对数据进行分类,对比了KNN和SVM分类性能。在每个数据集上选择波段的编号如表2~表4所示,可以看出,不同波段数对分类结果性能的影响,本文提出的方法在OA、AA和Kappa上面取得了比较满意的结果。当选择的波段数较小时,算法的精度不稳定,当超过20个波段时,算法的精度已趋于稳定。由图可知,SVM分类器的性能是远远优于KNN分类器的。相同条件下,SVM分类器的OA、AA和Kappa三个评价指标比KNN分类器更好。在Salinas valley数据上,最大相差的数值分别为2.81、2.24和3.45。在Pavia University数据集上,三个指标最大相差数值分别为5.89、6.51和8.18。在Indian pines数据集上,三个数值为12.19、18.05和14.2。由此可知,用SVM进行高光谱图像分类会比KNN具有更好的准确率。 表2 Salinas valley数据集选择的波段编号 表3 Pavia University数据集选择的波段编号 表4 Indian pines数据集选择的波段编号 为了更好地验证本方法的有效性与优越性,采用KNN和SVM作为分类器,并与MDSR、SOP-SRL和ASPS三种最新的算法进行实验对比,实验结果如图3、图4和图5所示。由图3可知,对于Salinas valley数据集,本算法在KNN分类器上OA系数一直高于其他算法。通过选择的不同的波段数,本算法在波段数很少的情况下就表现出了优秀的分类性能。本算法在选择5个波段的情况下,在Salinas valley和Pavia University数据集上的OA分别为88.02%和83.96%,此时的指标已经超过了MDSR、SOP-SRL和ASPS。但是随着波段数的不断增加,当波段增加到15个时性能不再出现明显的增长,这可能和子立方体包含的波段数越来越少导致当前波段无法得到更有利的信息进行判断和更新,说明了本方法在低维情况下更有效。在SVM分类器上,本算法在15个波段以前一直处于优势,随着波段数的不断增加,准确率也在持续上升。虽然后期的准确率不如SOP-SRL算法,但是此曲线相对平缓,并未出现较大的波段,此时本算法趋于稳定。由图4可知,对于Pavia University数据集,无论是在KNN分类器还是SVM分类器上,本算法的OA表现一直是高于其他算法的,这一点更加说明了本算法的优越性。与SOP-SRL和MDSR算法相比,本算法稳定性更好。对于Indian pines数据集,当波段数较少时,本算法在KNN分类器上的表现比其他算法好。而在SVM分类器上,ASPS和SOP-SRL具有更好的分类性能。MDSR算法分类的准确率明显不如其他几种算法,且该算法的稳定性也不如其他几种算法好。综上所述,本算法的综合表现是优于其他算法的,具有更好的稳健性,即使是在小样本的情况下也能有很好的表现。 图3 Salinas valley分类结果图:(a) KNN;(b) SVM 图4 Pavia University分类结果图:(a) KNN;(b) SVM 图5 Indian pines分类结果图:(a) KNN;(b) SVM 为了验证本算法的有效性与优越性,以15波段为例,分别对三个数据集的地物进行分类,分类结果如表5、表6、图6和图7所示。由表5可以看到,本算法的OA指数在Salinas valley和Pavia University数据集上都高于其他算法,相比于MDSR算法,分别提高了4.05%和5.09%。在Indian pines数据集上,本算法Kappa指标比MDSR高出9.29%。对于Salinas valley和Pavia University数据集,与SOP-SRL和ASPS算法相比,本文的AA和Kappa两个指标都存在一定优势。而对于SVM分类器的分类结果,如表6所示,在Salinas valley和Pavia University数据集上,本文算法相比于其他几种算法的OA 、AA和Kappa三个评价指标都是明显处于优势的,尽管在Indian pines数据集上的表现不是那么乐观,但是它相比于MDSR算法,优势依然很明显,这也充分说明了本算法的优越性。由图6和图7可以看出,本算法在Salinas valley和Pavia University数据集上分类的效果也明显好于其他算法,很少出现错分和漏分的现象,这与表格中的数据正好吻合。但是在Indian pines数据集上,本算法与其他对比分类的结果都不太理想,原因可能在于Indian pines数据所包含的地物种类繁多,且提供的样本数少。 表5 三个数据集上不同方法的分类结果(KNN) 表6 三个数据集上不同方法的分类结果(SVM) 提出了一种基于子空间划分和自我表示学习的高光谱波段选择方法,最大限度地利用类间距离与类内距离之比,将高光谱图像立方体分割为多个子立方体。采用自表示学习算法处理子立方体,采用记忆向量q进行波段选择,具有记忆功能的向量可以反映历史数据中的波段质量,以保持不同时间的数据之间的一致性,并指导后续的波段选择。通过在三个公开数据集上进行实验室对比分析,所提方法在OA、AA和Kappa三个指标上都具有很好的表现,从而验证了所提出的波段选择方法的可行性与有效性。
1.2 自我表示学习
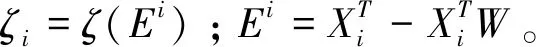
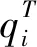
2 实验与分析
2.1 实验环境和数据

2.2 实验设置
2.3 实验结果分析











3 结 论
