不确定环境下交通网络应急预防护优化研究
2021-06-24陈学伟秦进周颖靓
陈学伟,秦进,周颖靓
(中南大学 交通运输工程学院,湖南 长沙 410075)
近年来,我国各类自然灾害频发,对社会和经济发展造成了严重破坏。由于灾害具有突发性,在目前条件下还很难对其进行控制和预防,因此如何保障灾后救援和疏散等活动[1],成为当前灾害应急管理研究中的热点问题之一。交通网络是灾后救援中发挥着巨大的作用[2]。但是其基础设施在受灾区域内也会受到损毁。从减灾和防灾角度出发,有必要在灾前对交通基础设施进行养护和加固,以提高其抗毁能力和保证灾后的服务能力。近年来,专家学者就交通网络的应急预防护问题开展了广泛的探讨。CHU 等[3]提出两阶段随机模型,最大限度提高公路网络的连通可靠性。LIU等[4]研究多条公路桥梁运输系统的鲁棒性和弹性,确保在未来的地震损失降至最小。YAN等[5]在预算有限的条件下,加强对中国铁路系统的投资,来最小化地震灾害造成的系统服务损失。YÜCEL等[6]提出灾前投资决策来加强网络的路段结构,通过降低路段受损概率来提高灾后网络可达性。在国内外相关研究中,都是将路段加固状态定义为0−1 变量,即仅考虑加固和不加固2 种状态。但是在实际工作中,根据相关工程作业标准,路段的养护是可以按照不同等级进行不同程度的加固[7],相应的其在灾害中的受损情况也并不一致。本文结合实际工程标准,研究不确定环境下的交通网络应急预防护优化决策方案。
1 问题分析
为了有效应对自然灾害给交通网络所带来的不确定风险,需要考虑在灾害发生前,选择对交通网络进行养护加固等预防护方案,以应对各种灾害情景,此即不确定环境下交通网络应急预防护优化问题。灾前养护和灾后维修通常需要大量的经济成本。极度严重的灾害通常发生的概率极低,将交通网络的所有路段养护加固到可以承受此类灾害的程度,会导致无法承受的支出。加之养护预算有限,如何合理分配有限的预算从而使交通网络的预防护效果最大化是该领域的关键问题。
为提高交通网络在灾害中的抗毁能力,更有效地保证其灾后的运输服务质量,考虑在灾前对路段等关键基础设施进行养护加固等预防护方案。交通网络应急预防护优化决策方案的关键目标是确定有限预算下交通网络各路段的养护等级。根据《公路养护技术规范》[8]对养护工程的规定,本文将养护等级分为0~4 共5 级,分别对应不养护、小修、中修、大修和改建5级养护工程。同时考虑了预算成本、网络连通性、旅行时间、通行能力等因素,从数学角度最小化灾前养护加固成本和灾后修复费用期望成本。通过优化分析确定最优养护方案,可以保证以最小的成本费用取得最大的防护效果,对灾后的救援、疏散及恢复有重大的意义。
2 模型构建
2.1 问题假设
为方便模型建立,可作如下合理假设:
1)假设灾害情景的发生概率是已知的;2)假设不受灾害影响的路段集合是已知的,该集合中的路段不需要进行养护加固。受灾害影响的路段集合则需要考虑在灾前进行养护加固;3)假设在受灾害影响的路段集合中,未养护的路段在灾害下毁坏,不能通行;已养护的路段在灾害下受损,路段连通但通行能力下降;4)假设灾害发生后交通网络的出行需求较灾前发生变化;5)假设灾后的人员疏散和救援工作是有序组织和开展的。
2.2 变量定义
G(N,A):交通网络;N:交通网络中的节点集合;A:交通网络中的路段集合,A=A1∪A2;A1:不受灾害影响的路段集合;A2:受灾害影响的路段集合;W:交通网络中所有OD对集合;Ω:所有可能灾害情景的集合;ω:交通网络可能面临的灾害情景,ω∈Ω;Pω:灾害情景ω发生的概率,xa:路段a上的流量,a∈A;ca:路段a上的通行能力,a∈A;:路段a的自由流阻抗,a∈A;ta(xa,ca):路 段a的交通阻抗,a∈A;qij:OD对[i,j]间的交通需求量,[i,j]∈N;Kij:OD对[i,j]间的有效路径集,[i,j]∈N;:OD对[i,j]间的路径k(k∈Kij)的流量,[i,j]∈N;σa:路段a的单位长度养护成本,a∈A;τa:路段a的单位长度修复成本,a∈A;la:路段a的长度,a∈A;ε:交通网络应急预防护的预算上限;T0:灾害发生前的交通网络总阻抗;Aω:灾害情景ω下的有效路径集,ω∈Ω;Tω:灾害情景ω下的交通网络总阻抗,其中ω∈Ω。
决策变量和状态变量定义如下。
ωa:灾害ω发生时路段a未受到影响,则为1,反之为0。
ya:路段a预防护决策变量,即对路段a的养护等级。

n:0−4的5类养护等级,分别对应不养护、小修、中修、大修和改建5级养护工程。
ya:若a∈A2,则ya等于n,若a∈A1,则ya等于0。
θa(ω):路段a在灾害情景ω下损坏的概率。其中,ϕa(ω)表示已经改建(ya=4)的路段a在灾害情景ω下损坏的概率,ξa(ω)表示未经养护(ya=0)的路段a在灾害情景ω下损坏的概率。
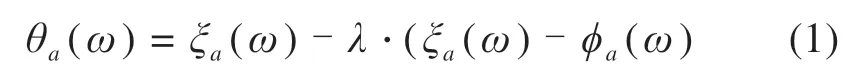
λ:以ya为自变量的分段函数。

表1 λ关于ya的分段函数Table 1 λ piecewise function with respect toya
根据路段a在灾害情景ω下的风险状态ωa和其预养护决策ya,确定灾后路段a的连通状态π(ωa,ya):
π(ωa,ya):路段a在灾后仍保持连通,则为1(∀a∈A1或∀a∈A2,ya≠0);反之,则为0,处于非连通状态(∀a∈A2)。
β:经过5级养护工程后的路段a(∀a∈A2)在灾害情景ω下的受损程度,可根据先验经验得出[9]。
C(ωa,ya):根据路段a在灾害情景ω下的风险状态ωa和其预防护决策变量ya,可以确定路段a的灾后通行能力[10]。当灾害情景ω发生时,若路段a不受灾害影响(∀a∈A1),其灾后通行能力仍为ca。若路段a受灾害影响(∀a∈A2),此时路段a的受损程度为β,其灾后通行能力降为ca⋅(1-β)。
2.3 优化模型
针对研究问题,建立交通网络应急预防护双层规划模型,其中上层模型为交通网络应急预防护决策模型,下层模型由各灾害情景下具有不同网络结构的交通均衡配流模型构成。优化决策将总成本最小化作为优化目标。
由此,交通网络应急预防护双层规划模型可以描述如下。
上层交通网络应急预防护决策模型:
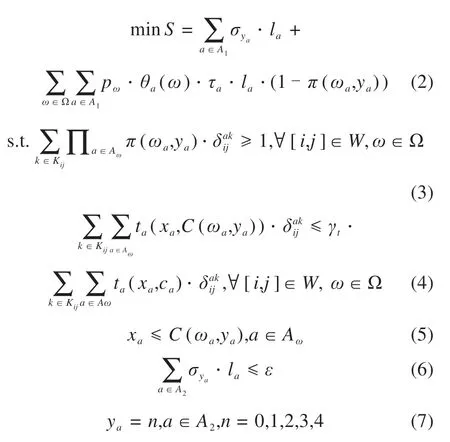
式(2)总成本包含灾前养护加固成本和灾后修复期望费用。式(3)确保至少存在一条路径k中的所有路段a的灾后连通状态π(ωa,ya)=1。式(4)确保任意OD对[i,j]的应急旅行时间与正常旅行时间的比值不超过时间可靠性系数γt。式(5)路段a的流量不超过该路段的灾后通行能力。式(6)满足养护预算约束。式(7)为养护等级。
下层交通均衡配流模型:

上层模型的优化目标是最小化交通网络的灾前养护加固成本和灾后修复期望费用,同时考虑预算约束、网络连通性约束、旅行时间可靠性约束、路段通行能力约束和决策变量的取值约束。灾害情景集合为Ω,即交通网络可能面临|Ω|种灾害情景,可能具有|Ω|种灾后网络结构。为满足|Ω|个灾后固定需求,下层交通均衡配流模型用来描述灾区人员的避险路径选择行为。μω是灾害情景ω下出行需求矩阵影响因子。系统将略去拥挤效应,路段上的阻抗不随流量变化,司机将选择一对节点之间的最小阻抗路径。因此下层模型可以使用“全有全无”算法进行求解。该模型上下层的联系在于上层模型中各路段的阻抗由下层模型求得。由此,上层的交通网络应急预防护决策模型和下层的交通均衡配流模型共同构成交通网络应急预防护决策优化双层规划模型。
3 算法求解
本问题属于NP 难问题,难以用精确算法和商业软件进行求解。本文研究基于Frank-Wolfe 的模拟退火算法(Simulated Annealing,SA)来设计本问题的求解方法。SA 算法具有使用灵活、描述方便、容易实现及计算效率高等特点,故选择SA 算法对上层交通网络应急预防护决策模型进行求解。选择Frank−Wolfe 算法对下层交通均衡配流模型进行求解[11]。SA 算法的关键是邻域构造。本研究采用变换1条路段的养护等级的方法进行邻域构造,图1和图2描述了上述领域操作。
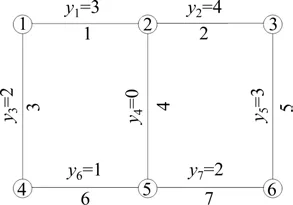
图1 当前解YFig.1 Current solutionY

图2 邻域解Y1Fig.2 Neighborhood solutionY1
求解上层模型的SA算法[12]的详细步骤如下。
Step 1:设置参数初始值。设置初始温度t0,温度下降比例为a,终止温度tf,同一温度下迭代限制次数L,初始迭代次数l=1。利用Frank−Wolfe 算法[19]对初始交通网络进行平衡配流,得到各路段阻抗ta(xa,ca)。
Step 2:确定当前解和目标函数S0。生成初始解-Y;获得灾害情景下的交通网络,数量为|Ω|,得到各路段连通状态和通行能力。利用下层模型进行平衡配流,得到各路段阻抗ta(xa,C(ωa,ya))和流量xa;判断的可行性。若满足上层模型约束条件,令当前解并计算上层模型初始目标函数S0;否则,重复Step 2。
Step 3:构造邻域解根据给定的邻域构造方法,得到当前解的一个邻域解确定预防护后各灾害情景下的|Ω|个交通网络,利用下层模型进行均衡配流,得到各灾害情境下各路段的阻抗和流量;判断的可行性。若满足约束条件,转Step 4;否则,重复Step 3。
Step 4:计算邻域解的目标函数值S1。根据所得可行邻域解,计算上层模型的目标函数S1。
Step 5:根据Metropolis 准则判断是否接受邻域解为当前解。计算ΔS1-S0。若ΔS0≤0,则接受邻域解为当前解,令,S0=S1。若ΔS0 >0,较劣解的接受概率为p(⋅)=exp(-ΔS/ti),从区间(0,1)随机产生一个数值γ,若γ Step 6:同一温度进行迭代。令l=l+1。若l≥L,转Step 7;否则返回Step 3。 Step 7:降温。根据降温规则,将当前温度值调整为ti+1=a⋅ti。 Step 8:判断收敛性。若当前温度ti+1 某灾害风险地区的交通网络如图3所示,该网络共有20 个节点,31 条路段,路段双向均有交通流。路段编号和节点编号如图,括号内的数值分别表示该路段的长度、通行能力和自由流阻抗,格式为 图3 算例交通网络Fig.3 Example transportation network 交通网络节点OD对间的出行需求是非对称的,具体数值如表2所示。 表2 5级养护工程后灾害下路段的受损情况Table 2 Damage situation of road section after disaster after the fifth-level maintenance project 表4~5 表示各灾害情景下,灾害发生的概率及路段的损坏情况,μω是灾害情景ω下出行需求矩阵影响因子。“1”表示未养护路段在灾害中未受损,反之则用“0”表示。 表3 OD出行需求Table 3 OD travel requirements 表4 各灾害发生概率及1~10号路段损坏情况Table 4 Probability of various disasters and damage of No.1~10 road sections 表5 各灾害发生概率及11~20号路段损坏情况Table 5 Probability of various disasters and damage of No.11~20 road sections 网络中路段阻抗的计算,采用通用的BRP 函数,其中k1,k2为常数,一般取k1=0.15,k2=4.0。设置交通网络应急预防护的预算上限ε=5 500,时间可靠性系数γt取0.8。同时设置模拟退火算法的初始温度t0=1 000,降温系数a=0.9,同温度迭代限制次数L=100,算法终止温度tf=0.01,较劣解p的接受概率取0.65。本文设计基于模拟退火算法和Frank-Wolfe 算法的求解方法,运用MATLAB 软件对模型进行计算。可以得到灾前路段养护加固成本和灾后修复费用的期望成本为S=4 819.73。算例结果如表8所示。 表6 各灾害发生概率及21~31号路段损坏情况Table 6 Probability of various disasters and damage of No.21~31 road section 表7 单位长度路段不同养护等级养护加固费用和维修费用Table 7 Maintenance and reinforcement costs and maintenance costs of different levels per unit length of road section 表8 算例结果Table 8 Calculation results 求解的最优应急预防护方案为: 分析该方案是否满足资金约束条件限制。灾前养护加固成本为3 002.6,小于路段养护加固预算上限5 500,故该方案满足资金约束条件。 分析该方案是否满足连通性约束条件限制。因OD对数较多,一一验证不太现实,故选取其中3 对进行分析。如9 所示,OD对(2,10),(13,17)和(19,20)间均存在至少一条连通路径,故满足连通性约束。 分析该方案是否满足通行能力约束。以灾害情景ω1为例,路段流量和路段通行能力的比值关系如图4所示。图例中,交通流起点的节点编号小于终点的节点编号,该路段称为正向路段,反之称为反向路段。当路段完全损毁,即不连通时,该路段无法通行,通行能力降为0,该路段的流量为0,满足约束。如图4 所示,路段流量和路段通行能力的比值均小于1,满足通行能力约束。 图4 灾害情景ω1下各路段的x/cFig.4 Various road sectionsx/cunder the disaster scenario ω1 分析该方案是否满足旅行时间可靠性约束。由假设可知,司机将选择一对节点之间的最小阻抗路径。选取OD对(17,13)和(19,20)进行分析,如表9所示。 表9 连通性约束Table 9 Connectivity constraints 当路段完全损毁,即不连通时,该路段无法通行,路段旅行时间为∞,但该路段一定不处于连接OD对的路径上,故为0,满足约束。OD对(17,13)和(19,20)间灾后最小阻抗路径的旅行时间与灾前最小阻抗路径的旅行时间的比值均小于0.8,满足旅行时间可靠性约束。 表10 旅行时间可靠性约束Table 10 Travel time reliability constraints 1) 针对交通网络应急预防护问题,提出交通网络预防护双层规划模型,设计基于Frank-Wolfe的模拟退火算法进行求解,以某受灾区域为例进行分析,优化结果良好,具有较好的运算效率和收敛性。提出的方法为决策者提供理论依据。算例分析表明,养护后的交通网络在灾害下的抗毁能力大为提高。同一灾害情景下,灾后网络连通性、路段通行能力和旅行时间可靠性等指标与未经养护的交通网络相比,其性能更为突出。 2)当前既有研究仅将路段考虑加固和不加固2种状态。但现实生活中,受到养护成本等一系列因素的限制,对交通网络的每一路段进行最高程度的加固并不现实。本文提出将养护等级细分为0~4 共5 级,分别对应5 级养护工程,增加了模型的现实可行性,为养护优化方案提供了更多的可能性。4 算例分析
4.1 算例简述
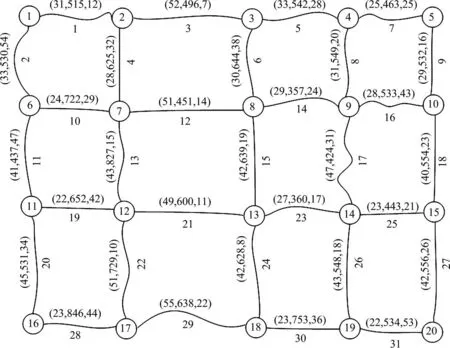




4.2 算例结果及分析






5 结论
