基于可变模糊集理论的铁路隧道塌方风险评价
2021-06-24王婧靳春玲贡力张鑫
王婧,靳春玲,贡力,张鑫
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
我国铁路隧道建设正不断向着更大规模、更高标准的方向发展,复杂的地质条件以及施工新技术的应用等都会造成隧道施工各类风险因素的增加。塌方事故作为铁路隧道建设中最常见、最具代表性的风险之一,其对隧道施工过程有着十分重要的影响,隧道塌方不仅会使隧道施工更加困难,而且还可能影响到工程设备的正常运行以及施工人员的生命安全,造成工程经济损失和不良的社会影响。因此,对铁路隧道塌方风险进行评价研究,对保障隧道施工进度及施工安全具有重要意义。在我国隧道塌方风险研究中,袁永才等[1]结合我国近300 例隧道塌方案例建立了隧道塌方风险评价指标体系,运用突变理论对红岩寺隧道塌方风险进行了评估,并提出了相应的隧道塌方治理方案;徐海清等[2]建立了一种可预测隧道塌方时间的尖点突变失稳预测模型,并结合实际案例对软岩隧道围岩塌方风险进行了预测研究,预测结果与实际基本一致;王秋生等[3]以黄陵—韩城—侯马铁路如意隧道为依托,分析了隧道塌方的影响因素,提出了隧道塌方的处置措施,并通过数值模拟对塌方处置效果进行了评价;孟超等[4]运用SVM 模型分析了铁路隧道塌方事故中常见的18个风险因素的关系,通过计算各风险因素信息熵得出地下水渗流、特殊不良地质、开挖方式是影响隧道塌方的主要因素。以上研究为铁路隧道塌方风险的研究提供了重要的研究方法和研究成果,但其中仍存在部分问题亟需进一步研究,如传统权重分配方法对评价指标权重分配的合理性、评价模型对评价目标的适用性等。铁路隧道塌方风险评价是一个多指标、多级别的综合评价问题。基于铁路隧道塌方风险因素的复杂性、模糊性以及不确定性,本文选用可变模糊集理论,建立了可变换模型参数的隧道塌方风险可变模糊集理论模型,并结合博弈论组合赋权法优化赋权,弥补了单一主观赋权或客观赋权的不足。运用工程实例验证了评价模型的可行性,并对风险评价结果进行了分析。可变模糊集理论模型具有理论严谨,精度较高的优点,通过模型参数的变换,大大提高了铁路隧道塌方风险评价结果的可靠度,相较于传统评价模型,可变模糊集理论模型评价结果精度更高,工程适用性良好,能够为铁路隧道塌方风险评价提供新的参考。
1 风险评价指标体系与等级划分标准
1.1 铁路隧道塌方风险评价指标体系
在铁路隧道施工过程中,影响隧道塌方的风险因素较为复杂,各影响因素之间存在一定的关联性和模糊性。为便于准确选取隧道塌方风险评价指标,本文通过既有研究成果[5−8]及相关标准,综合考虑指标的影响力、代表性以及可量化性等,从铁路隧道工程地质、勘察设计、施工技术与管理水平3个主要影响方面出发,构建了包括工程地质4 个2 级指标、勘察设计4 个2 级指标、施工技术与管理2 个2 级指标共10 个2 级评价指标的铁路隧道塌方风险评价指标体系。其中,地质勘察深度、施工对围岩的扰动、施工技术水平、施工管理水平4 个2 级指标属于定性指标,其余6 个2 级指标为定量指标,隧道塌方风险评价指标体系如图1所示。
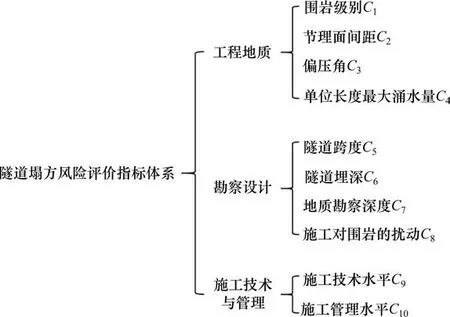
图1 铁路隧道塌方风险评价指标体系Fig.1 Risk evaluation index system of railway tunnel collapse
1) 在工程地质影响因素中,围岩级别对隧道塌方有着直接影响,一般来说,围岩级别越低,塌方风险越大;岩体中部分节理发育较深,具有明显的方向性与规律性,对地下水及隧道施工影响显著,节理面间距越小,岩石破碎程度越大,塌方风险越高;隧道洞口浅埋段常因地形情况而产生偏压,对围岩稳定性产生影响,一般情况下,山体倾角越大,塌方风险越高;地下水能溶蚀岩体结构面的胶结物及充填物,降低岩体强度,从而降低围岩稳定性,地下水越发育,隧道塌方风险越高,本文以单位长度最大涌水量来表示地下水情况。
2) 在勘察设计影响因素中,隧道开挖跨度与塌方风险成正比,开挖跨度越大,隧道开挖的应力扰动区内节理组数越多,岩体破碎程度越大,围岩稳定性降低;隧道埋深与塌方风险成反比,隧道埋深越浅,隧道开挖中越难以形成相对稳定的自然拱,围岩自稳能力差,容易产生大变形;地质勘察情况影响着隧道设计参数的选择,地质勘察越详细深入,隧道设计参数选取就越合理,塌方风险就越低;施工对围岩的扰动是一项不可避免的风险因素,围岩扰动范围越小,隧道塌方风险就越低。
3) 在施工技术与管理影响因素中,施工技术水平和施工管理水平均属于人为因素,施工的合理性与规范性对隧道塌方具有直接影响,施工技术水平与施工管理水平越高,隧道塌方风险越小。
1.2 铁路隧道塌方风险评价等级划分标准
根据常规风险评价等级划分标准、隧道塌方特征及相关文献[9−11]将隧道塌方风险等级划分为4 级,依次为低风险(1 级)、中风险(2 级)、高风险(3 级)、极高风险(4 级)。其中低风险表示风险可被忽略,按照预定施工方案进行施工即可;中风险表示风险在预期范围内,可通过一定手段进行风险的规避与处理;高风险表示风险超出预期,需要加以重视,应检查施工过程的规范性,重新设计风险应对方案;极高风险表示风险有极高的可能性会发生,应立即停止施工并进行风险专题论证,设计合理方案进行整改,以避免塌方事故的发生。
隧道塌方风险评价指标等级的划分依据相关行业标准以及既有研究成果[1−4],在结合铁路隧道工程概况下进行划分,得到最终的铁路隧道塌方风险评价指标分级标准如表1所示。

表1 铁路隧道塌方风险评价指标分级标准Table 1 Classification standard of risk assessment index for railway tunnel collapse
2 可变模糊评价模型
2.1 博弈论组合赋权法
权重分配的合理性对风险评价结果至关重要,本文兼顾权重分配的主观性与客观性,分别应用改进的G2 法和改进的CRITIC 法进行主、客观赋权,结合博弈论组合赋权法优化赋权,根据优化得到的指标综合权重在可变模糊评价模型中对隧道塌方风险进行综合评价。
2.1.1 改进G2法
G2 法的核心思想是依据评价指标间的重要程度之比来判断指标的权重值[12]。为减少专家个人因素对指标权重的影响,本文应用指标基尼系数之比代替专家意见判定的指标重要度之比,具体计算步骤如下:
1)对指标样本数据排序,计算各指标xi的基尼系数Gi。
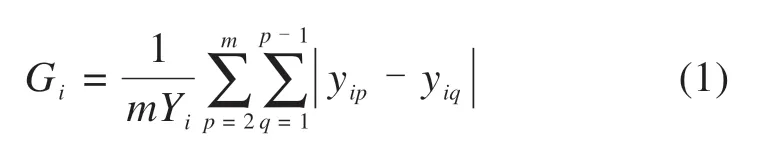
其中:m表示样本数目;yip,yiq为指标xi对应的第p,q个样本值,Yi表示指标xi样本数据之和。
2)从指标集X={xi}(i=1,2,…,n)中选取最不重要指标xt,计算各指标对xt的相对重要程度ri:

其中:Gt表示最不重要指标xt的基尼系数。
3)计算各评价指标xi的主观权重:

2.1.2 改进CRITIC法
CRITIC 法是一种通过指标的对比强度和冲突性确定指标权重的客观赋权方法。为更好地反映评价指标间的关系,本文采用标准差系数代替传统计算中的标准差来表示指标对比强度,同时对传统计算中指标相关系数取绝对值来表示指标冲突性[12]。改进的CRITIC法计算步骤如下:
1) 对指标样本数据运用极差法进行标准化处理。
2)计算指标xi所含信息量Ci:

3)计算评价指标xi客观权重:

2.1.3 博弈论组合赋权法
通过博弈论组合赋权,可以避免单一权重分配方法的片面性,提高权重分配的合理性与准确性,同时兼顾主观与客观赋权各自的优势,使评价指标权重分配达到主客观统一[13]。其详细步骤如下:
1) 设L种权重方法线性组合的综合权重向量Wz为:
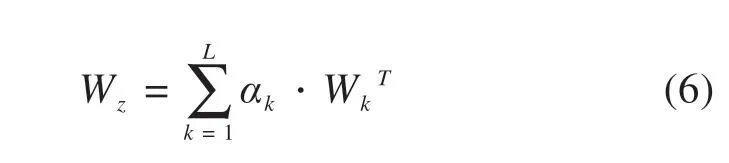
其中:αk为组合系数,Wk=(wki)(k=1,2,…,L,i=1,2,…,n)为各权重方法权重。
2)优化组合系数αk得到对策模型如式(7)所示,其转化为最优一阶导数的条件如式(8)所示:

3)结合式(8)计算得(αk)(k=1,2,…,L),对其归一化处理如下:

4)计算评价指标xi最优综合权重:

2.2 可变模糊评价法
可变模糊集理论是陈守煜教授在2009 年提出的,该理论基于模糊水文水资源学提出,目前已经在众多领域进行应用,具有广阔的应用前景[14−16]。本文基于该理论对铁路隧道塌方风险进行评价,详细计算步骤如下[15]:
1)设有m个评价样本,n个评价指标组成的样本特征值矩阵X=(xij)(i=1,2,…,n;j=1,2,…,m),样本评价等级h=1,2,…,s,则有指标标准值区间矩阵为

2)确定区间[aih,bih]中相对隶属度等于1 的点值矩阵M=(Mih):
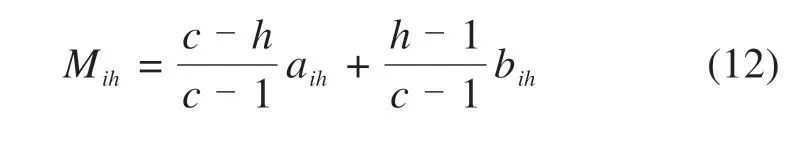
3)根据待评样本j指标i的特征值xij与级别h指标i的Mih值进行比较,指标分布区域示意图如图2所示,若xij落在Mih的左侧,其相对隶属函数计算如式(13)所示,若xij落在Mih的右侧,相对隶属函数计算如式(14)所示:

图2 指标分布区域示意图Fig.2 Schematic diagram of indicator distribution area
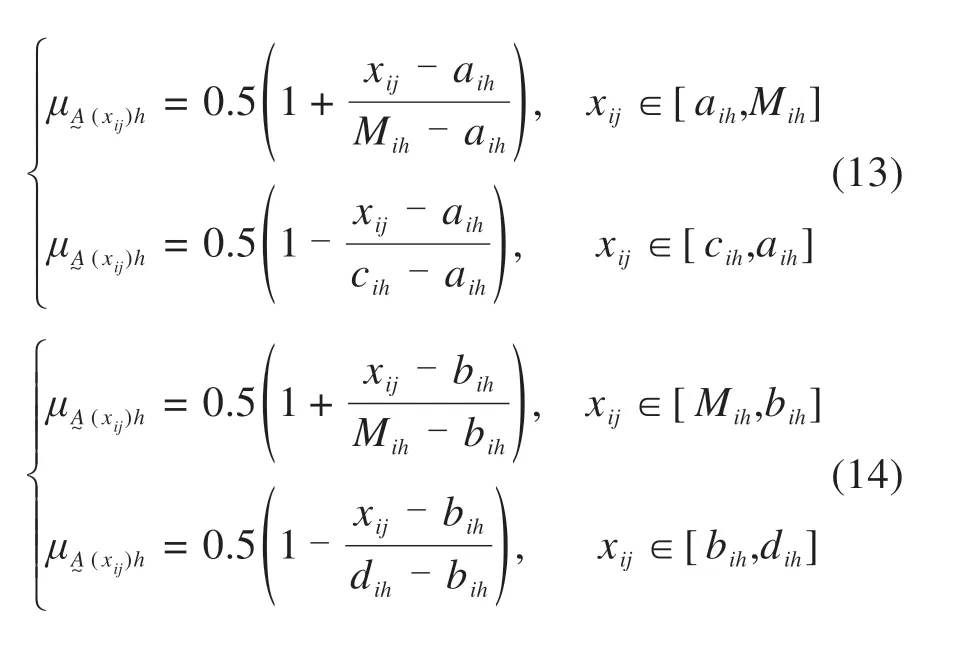

式中:ωi为指标权重;α为准则参数;v为距离参数;α,v通常有以下4种组合:
当α=1,v=1 时,该公式变为模糊评价模型;当α=1,v=2 时,该公式变为TOPSIS 理想点模型;当α=2,v=1 时,该公式变为神经元激励函数模型;当α=2,v=2 时,该公式变为模糊优选评价模型。由此构成一个4种组合的可变模糊集。
5)归一化处理后的综合相对隶属度:

6)计算样本j的级别特征值向量Hj,根据Hj及其平均值对样本进行综合评价:

2.3 可变模糊评价模型
结合上述理论,得到铁路隧道塌方风险评价流程如图3所示。本文首先通过分析铁路隧道塌方风险因素建立了铁路隧道塌方风险评价指标体系,然后运用改进的G2 法和CRITIC 法对指标进行主客观赋权,结合博弈论组合赋权法优化赋权得到指标综合权重,最后,应用4种模型参数组合下的可变模糊评价法综合判断铁路隧道塌方风险等级。
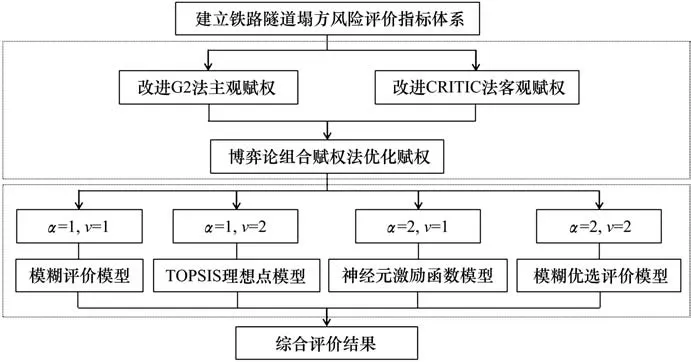
图3 铁路隧道塌方风险评价流程图Fig.3 Flow chart of risk assessment of railway tunnel collapse
3 实例分析
3.1 工程概况
岩山隧道位于湖南省怀化市麻阳县兰村乡境内,起讫里程为DK204+341.54~DK206+316.5,隧道全长1 974.46 m,隧道洞内设单面坡,最大埋深约105 m。隧道地貌类型为丘陵地貌,地势起伏较大,丘间呈“V”或“U”字型的狭长沟谷较多,且沟谷内多发育溪流,丘坡表层覆盖有粉质黏土,植被较为茂密,坡体局部较陡峭,自然坡度为15°~37°。海拔标高为185~290 m。
3.2 权重计算
本文根据岩山隧道地质说明、设计说明以及地质超前预报,选取隧道主要5个区段作为评价样本,得到各样本评价指标实际数据如表2所示。

表2 样本评价指标实际数据Table 2 Actual data of sample evaluation indicators
结合以上数据,运用基尼系数改进后的G2 法计算评价指标主观权重,运用标准差系数改进的CRITIC 法计算评价指标客观权重,最后运用博弈论组合赋权法优化综合赋权,得到岩山隧道塌方风险评价指标综合权重,各评价指标权重计算结果如表3所示。
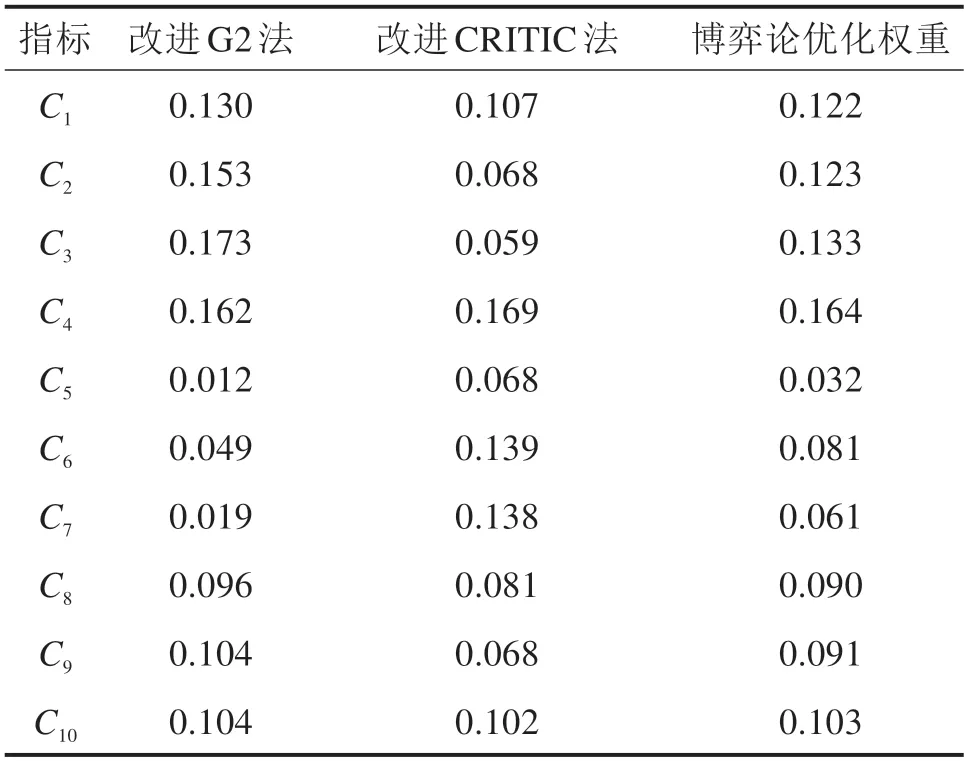
表3 铁路隧道风险评价指标权重Table 3 Index weight of railway tunnel risk assessment
3.3 可变模糊评价法计算
结合前文计算结果,以岩山隧道进口段为例,运用可变模糊评价法对隧道塌方风险等级进行评价,详细计算过程如下所示(其余各区段样本计算方法相同,在此不一一列出)。
1)结合表2样本评价指标实际数据,得到待测样本特征值矩阵如下:
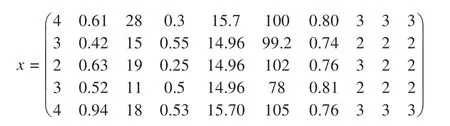
2)根据表1评价指标分级标准,可得隧道塌方风险评价指标标准值区间矩阵为:

根据式(12),计算Mih值得到隶属度为1的点值矩阵,判断指标数据xij落在Mih值的左端还是右端,结合式(13)和式(14),计算样本指标对评价级别的相对隶属度,归一化处理后得到的归一化隶属度矩阵为:

4) 应用式(15),结合博弈论优化综合权重值,求得α 和v4 种参数组合下样本j对级别h的综合相对隶属度,再结合式(16)~(17)求得级别特征值H,如表4所示。
5)根据表4 可计算得4 种模型参数组合下级别特征值平均值为Hˉ=2.695,即隧道进口段塌方风险等级偏向于3 级,说明隧道塌方风险处于高等风险,同理可得该隧道其余区段评价结果,如表5所示。

表4 4种模型参数组合下综合相对隶属度Table 4 Comprehensive relative membership under the com‐ bination of four model parameters
根据表5 评价结果可知,岩山隧道洞身DK204+450~DK204+715 段风险等级偏向于2 级,属于中等风险;DK205+580~DK205+670 段风险等级基本为2 级,属于中等风险;DK206+000~DK206+220 段风险等级偏向于2 级,属于中等风险;隧道出口段风险等级偏向于3级,属于高等风险。根据岩山隧道工程实际情况,隧道进出口段地质复杂,塌方影响因素多,风险较大,隧道洞身DK205+580~DK205+670 段地质情况较为简单,塌方风险较其他段低,DK205+580~DK205+670,DK206+000~DK206+220 段地质情况属于中等复杂,存在一定的塌方风险,因此可判断该风险评价结果合理。

表5 隧道塌方风险评价结果Table 5 Tunnel collapse risk evaluation result table
4 结论
1) 结合隧道工程施工情况,针对铁路隧道施工中的塌方问题,从工程地质、勘察设计、施工技术与管理3 个主要方面进行塌方风险因素分析,综合考虑评价指标的影响力、代表性及可量化性,建立铁路隧道塌方风险评价10 个2 级指标,构成了一套完整的铁路隧道塌方风险评价指标体系。
2) 基于改进的G2 法和CRITIC 法对评价指标进行主、客观赋权,运用博弈论理论对主、客观权重进行优化,避免了单一权重分配方法的片面性和绝对性,同时也兼顾了权重分配的合理性与准确性,使得权重分配达到最优。
3) 通过建立铁路隧道塌方风险评价的可变模糊集理论模型,结合岩山隧道进行实例分析,得到岩山隧道各区段塌方风险评价级别在2 级和3 级之间,隧道整体风险为中等风险至高等风险,风险级别在可控的风险范围内,评价结果与隧道实际情况一致,说明该模型具有一定的准确性与适用性,可在隧道塌方风险评价中进行应用与推广。
