研究状态机制转换下带有食饵避难响应的随机Leslie-Gower捕食模型

焦 媛，靳海娟，张秀锋

（长治学院数学系，山西长治 046011）

生态学和生物数学在人口预测、保护珍稀物种、生物资源的开发与利用方面有很重要的研究价值，而生物种群中最常见的捕食系统因此也具有普遍的存在性和重要性。最常用的两个物种的Leslie-Gower捕食模型：

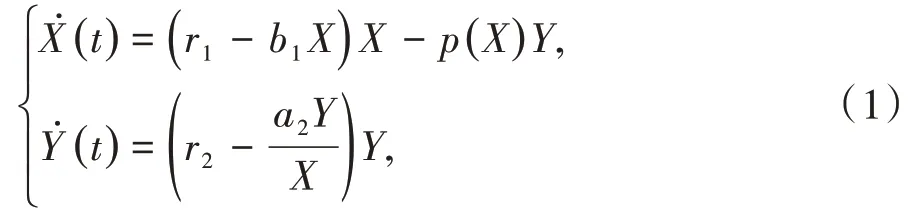
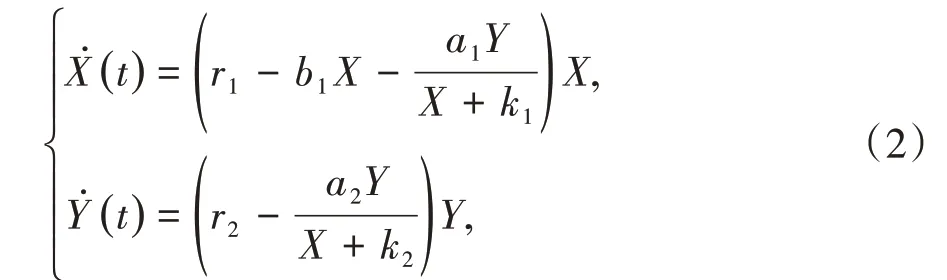
再通过加入环境或人为对被捕食者的保护mx来拓展模型(2),改进的模型为：

考虑到环境中的随机波动的影响，在系统(3)的每一个方程中都引入高斯白噪声来模拟环境影响[1-3],再假设环境的波动主要体现在捕食者和被捕食者的物种数量增长率的波动,，这里的均表示相互独立的布朗噪声,α 和β代表的是各物种增长率受到的白噪声的强度,接着对应于确定性模型系统(3),则随机系统有以下形式：

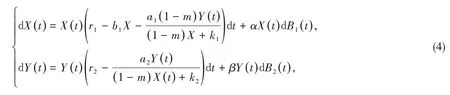
由于系统受到环境或自然界中会出现状态机制发生巨大变化的情形。例如：地震、环境骤变、极端天气等造成的影响，所以仍需进一步的研究。要考虑状态机制的转变导致物种结构的改变,引入马尔可夫链,设γ(t)，t ≥0 是在概率空间中的一个右连续的马尔可夫链,在一个有限的状态空间S={1,2,…,N} 中取值的以及它的发生器Γ=(ξij)N×N则有以下

假设马尔可夫链γ(·)是独立于布朗运动B(·)。也可以任意修改初始值γ(0)=i0∈S，所以可以得到对于任意的马尔可夫链是固定的。众所周知,几乎所有γ(·)的样本路径都是一个右连续的阶梯函数,在区间R:=[0,∞)的任何有限的子区间内都是有有限个样本跳跃。

由系统(5) 描述的捕食模型的活动机制可以解释为如下方程。假设最初的值为γ(0)=i ∈M，那么模型(5)满足

一直到γ(t)跳转到另一个状态才会改变。当跳转到新的状态称之为j ∈M之后,模型将变为

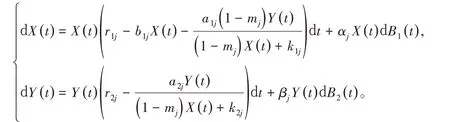
运用伊藤公式和解随机微分方程的方法,来证明随机系统的全局正解的存在性和唯一性以及物种数量的有界性；再利用马尔可夫链的遍历理论和鞅的强大数定律研究以及证明其物种的灭绝性和持久性。

1 全局正解的存在性和唯一性

定理1给定初值(X(0),Y(0))∈,系统(4) 在t ≥0上有唯一解(X(t),Y(t)),在上的概率为1。

证明在系统(4)中,引入新的变量U(t)=ln X(t)和W(t)=ln Y(t)并且应用伊藤公式,得到如下转换系统：

系统具有初始值为U(0)=ln X(0)，W(0)=ln Y(0)。显然地，式(6)的系数满足局部的利普希兹条件；因此，方程存在一个唯一的局部解(U(t),W(t))t ∈[0,τe)，这里的τe代表的是数量激增时间[4]，最后得到X(t)=eU(t)，Y(t)=eW(t)是系统(4)基于正初始条件下的唯一的局部解。只需要证明得τe=∞即可。

通过随机方程的比较定理[3],可以得到当时t ∈[0,τe)时X(t)≤φ(t)，Y(t)≤ψ(t)。

假设有τe＜∞,那么则就有存在一个T ＞0 有不等式P(τe＜T)＞0 成立而且令ω ∈(τe＜T)。从文献[3]中的定理A2,有

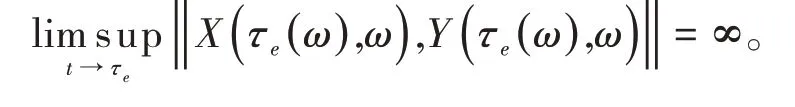
因此

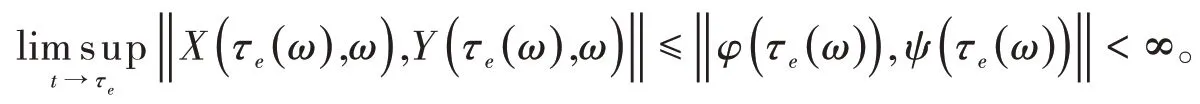
这个与已知的条件是矛盾的,所以有τe=∞。

2 有界性

定理2给任意初值(X(0),Y(0))∈，系统(4)的解X(t),Y(t)，均有以下性质：

(i)对于任意给定的正常数p,有

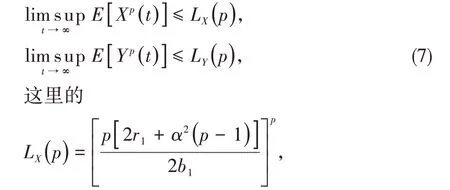
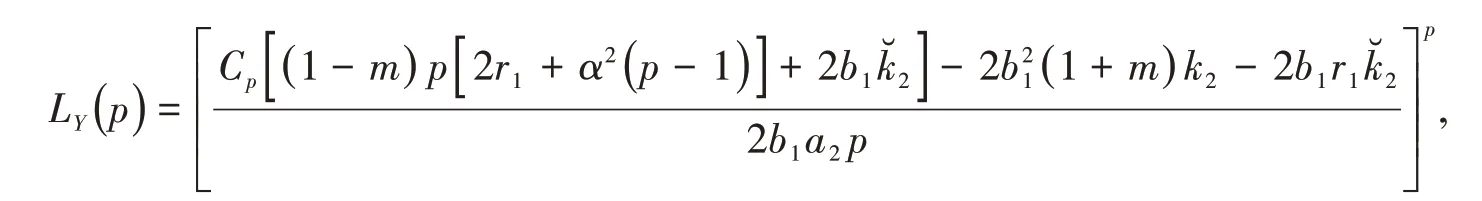
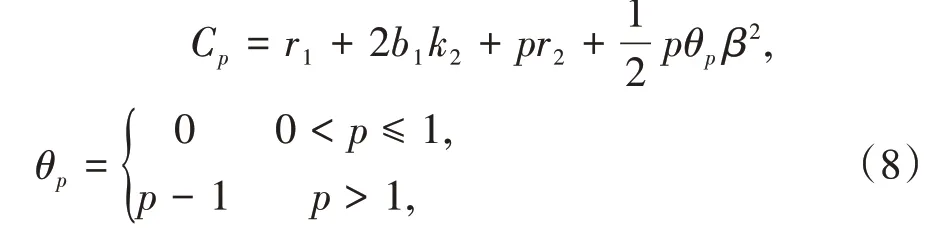
(ii)如果对于任意的ε ＞0,对于任何的初始数据(X(0),Y(0))∈均存在一个常数,且有

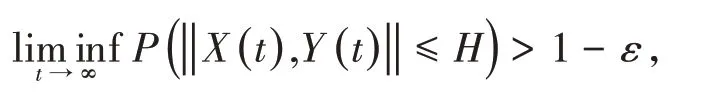
系统(4)的解则称为随机有界的。

证明(i)由于伊藤公式,可以得到

接着对方程的两边做积分有

再利用随机积分[5-6]的性质,可得

考虑不等式(9),可以得到

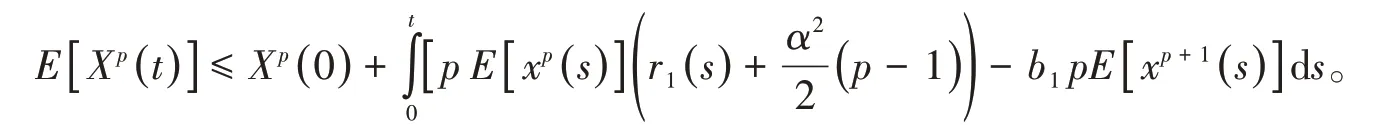
关于t的导数为

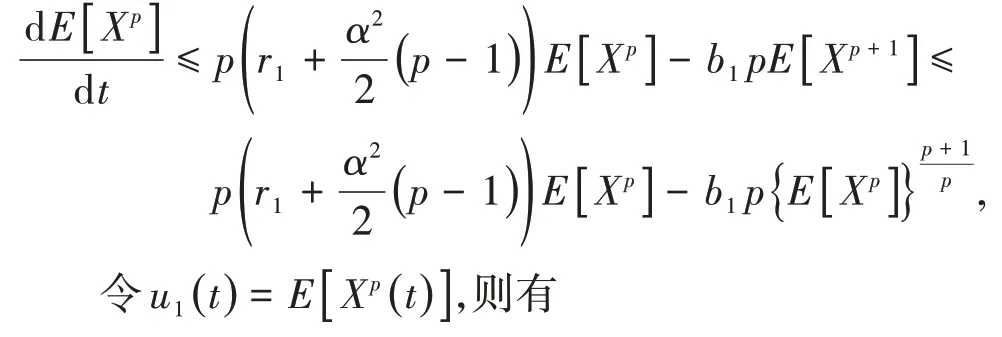
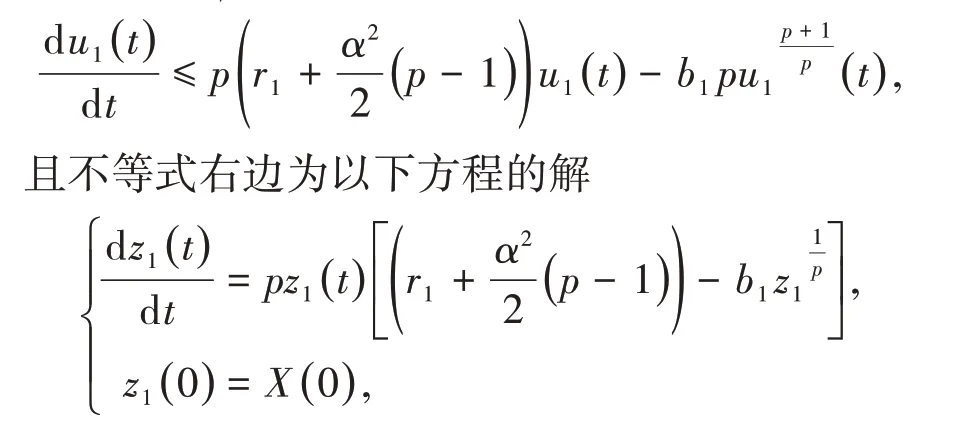
由伊藤公式,可以得到

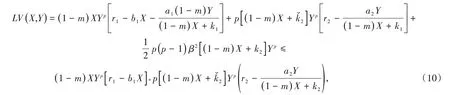
重新排列方程(10),可以得到

这里的Cp在式(8)中被定义以及

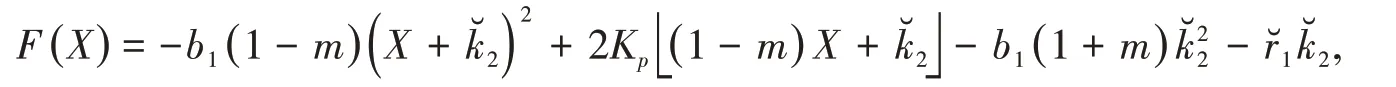
因为有

3 灭绝性和持久性

关于加入马尔可夫链系统(5)的性质,当状态机制发生转变系统是否具有稳定性。

定理3(i)若＜0,在捕食者灭绝的情况下,被捕食者的数量短期内呈指数级增长依概率收敛于1,即为

证明(i)由于伊藤公式,我们化简系统(5)的第一个方程得

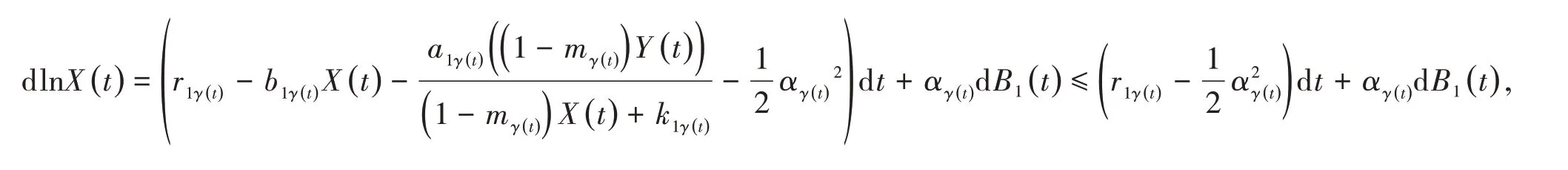
对上式两边做积分,可以得到

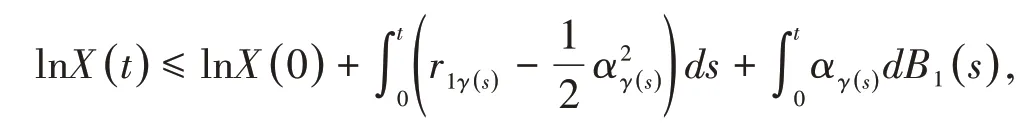
再通过马尔可夫链的遍历理论以及鞅的强大数定律,可以分别得到以下等式

(ii)类似于(i)的证明，运用伊藤公式化简系统(5)的第二个方程，得到关于ln Y(t)的等式。

证明得余下部分与(i)的证明相似故省略。

4 结语

主要研究了在随机扰动和状态转变下,带有食饵避难响应的Leslie-Gower 捕食系统.分别研究并证明系统的全局正解的存在唯一性以及物种数量的有界性,表明此系统是符合生物生态学的,具有可研究性.证明物种的灭绝性和持久性,表明在环境扰动和状态突变的情况下,只要物种保持在一定数量状态,那么最终一定会趋于稳定。