降阶型热波方程解的存在性和唯一性

金雪莲，张思佳

（1.辽宁工业大学 理学院，辽宁 锦州 121001；2.渤海大学 理学院，辽宁 锦州 121013）

在日常的生活生产中，系统的稳定性一直是研究的热点问题，在理论和实际问题中都扮演着重要的角色。由于在最优控制的数值计算问题中，经常要应用系统的一致指数稳定性，因此学者们对于系统是否稳定，以及不稳定的系统采用什么方法才能达到稳定等问题进行深入研究。在过去的几十年中，波方程的一致指数稳定性得到了广泛研究，本文不但解决了波方程的这个问题，而且将一些相关的结果推广到热波耦合系统中。

本文讨论了具有边界观测和同位控制的热波耦合系统的一致指数稳定性，首先对具有动态边界阻尼的热波耦合方程通过引入合适的中间变量，对其时间变量和空间变量进行降阶处理，写成与其等价的抽象微分方程的形式，接下来，在Hibert 空间上介绍了连续系统的状态空间以及定义在其上的内积和与其对应的能量空间,然后通过算子半群理论证明降阶后的方程的解存在性和唯一性,为后续引入Lyapunov 函数证明连续及离散系统的一致指数稳定性提供必要的前提和理论基础。

1 将热波方程降阶

本文研究的是如式(1)所示具有动态边界阻尼的一维热波方程，(y0,y1)是初始状态，w∈Rn是控制器 的状态，A∈Rn×n是常数矩阵，b,c∈Rn是列向量，d是正常数，y(t,x)表示弦在x∈(0,1)，t≥ 0时的位置。

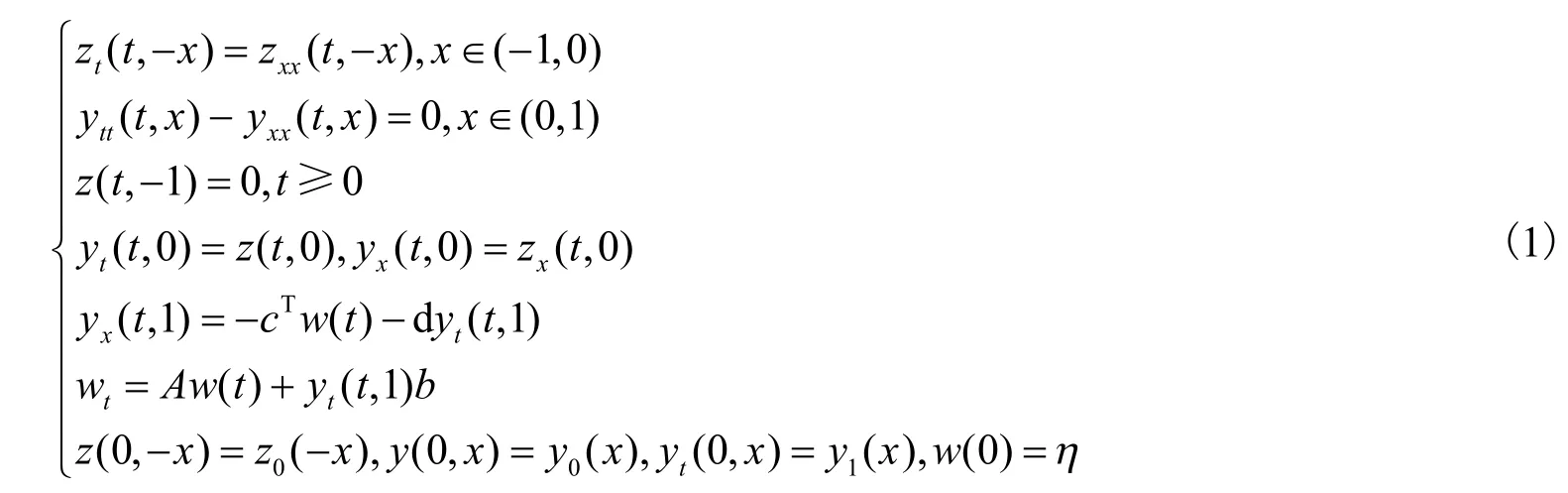
设系统(1)的能量

现将系统(1)进行降阶处理，引入两个中间变量：u(t,x)=yx(t,x)，v(t,x)=yt(t,x)，进而得到与系统 (1)等价的降阶形式，即

设系统(3)的状态空间为：H=L2(0,1)×L2(0,1)×L2(0,1)×Rn，H具有的内积如式(4)所示。

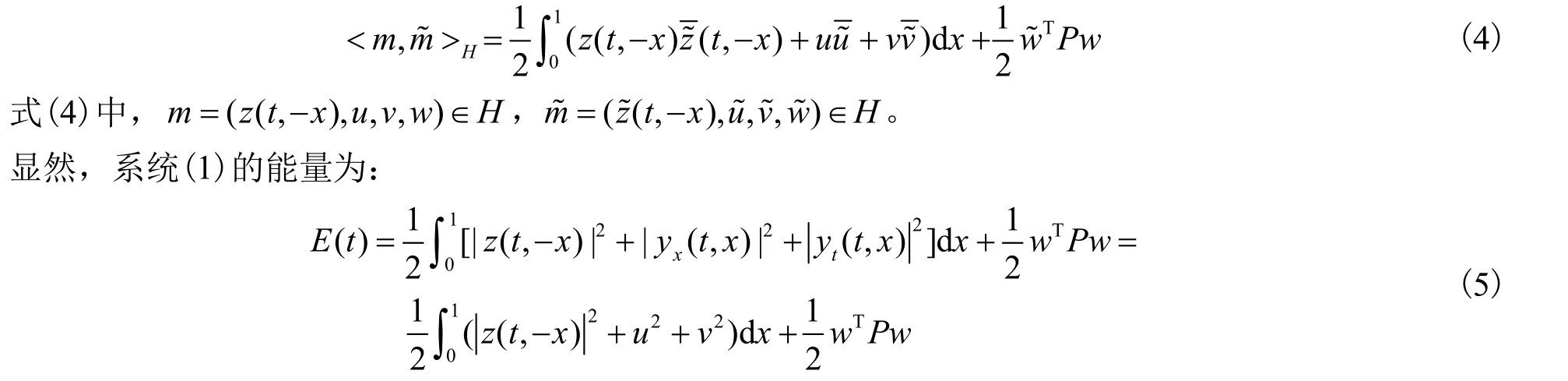
2 降阶后方程解的唯一性

本文结果依赖于如下假设[1]：

(1)矩阵A的所有特征值有负实部；

(2)),(bA是可控的且),(Ac是可观的；

(3)存在另一常数γ≥ 0使得d≥γ且d+RecT(isI-A)＞γ。

在这几个假设下，系统(1)的传递函数g(s)=d+cT(sI-A)-1b是正的实数。

由Meyer-Kalman-Yakubovich 引理[2]可知，Q∈Rn×n是任意的对称正定矩阵，一定存在对称的正定矩 阵P∈Rn×n,向量q∈Rn,Δ 为大于0 的常数，满足：

将系统(3)写成抽象微分方程的形式：

火草布虽然有一定的经济价值，但现阶段未完全挖掘出来，也并未带来实际的经济效益，导致年轻人不愿意去学习这门传统手工艺，大量年轻人外出务工，造成传承人断层现象。要使火草布获得一定的经济效益就必须使其进入市场，在如今整个市场的大环境下，必须使产品具有独特的品牌特色，依靠专业服务和质量管理，形成系列化和品牌化的经营模式。

定义1[3](耗散算子)：若线性算子A:D(A)⊂X→X对任意的x∈D(A)有：Re＜Ax,x＞≤ 0,则算子A被称为耗散算子。

定义2空间H=L2(0,1)×L2(0,1)×L2(0,1)×Rn,其内积：

定义3[4]设X、Y是线性赋范空间，X*、Y*分别是X与Y的共轭空间，算子T∈B(X,Y)，算子T*:Y*→X*称为T的共轭算子，是指对任意的x∈X*、y∈Y*，有(Tx,y*)=(x,T*y*)。

引理1[3]若A是Hilbert 空间上的线性稠定闭算子，则A是X上的收缩半群(T(t))t≥0的无穷小生成元的充要条件为:A和A*是耗散算子。

引理2[5]若A是C0半群(T(t))t≥0的无穷小生成元，那么对任意的x0∈D(A)，映射t|→T(t)x0是抽象微分方程

的唯一解。

定理降阶热波方程

存在唯一解。

证明

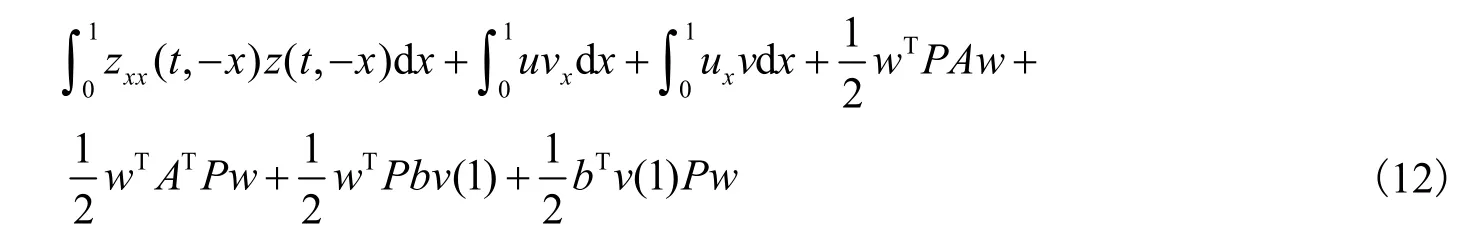
其中，由分部积分法：

将式(6)～(8)代入式(9)得：

根据定义1 得B是耗散算子。

由此可得：

所以算子B在H上生成的半群是收缩的0C半群。进而得出由算子B生成的半群)(tT是收缩半群。由 引理2 得系统(3)的唯一解可以由0)(XtT给出。并有系统(3)能量的导数：

证毕。

3 结束语

首先对具有动态边界阻尼的热波方程采用降阶处理，接下来，在Hibert 空间上介绍了连续系统的状态空间以及定义在其上的内积,然后通过算子半群理论证明降阶后的方程的解存在唯一性,为后续验证连续系统的一致指数稳定性和离散系统的一致指数稳定性提供必要的前提和理论基础。