基于纯相位加密的彩码加密系统研究

刘媛倩，陈林飞

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

随着时代的发展，信息安全成为重要的研究领域，图像加密是其中重要的组成部分。1995年，Refregier等[1]提出双随机相位编码技术后，光学图像加密得到广泛关注，大量的光学图像加密方法被提出，例如，Situ等[2]将双随机相位编码技术应用在菲涅尔域，Alfalouand等[3]提出利用双随机相位编码技术实现图像加密的多路复用，Sui等[4]提出一种应用分数傅里叶变换和干涉原理实现图像加密的方法，解决了干涉加密方法中存在的轮廓问题，Lim等[5]提出一种通过控制振幅和相位制作全息彩色印刷的方法，Jin等[6]提出一种对全息图进行编码的方法，Scheuer等[7]提出一种光学全息安全标签的制作方法。纯相位加密系统使用光的相位信息对图像进行编码，该方法将图像信息转换为光的相位信息，使用一个随机相位板对其进行加密[8-9]。但光学加密方法很容易将噪声引入图像，为此，文献[10-11]使用二维码作为光学加密的输入图像，消除了加密过程中产生的噪声。近年来，二维码也被广泛用于光学图像的加密[12-13]。彩码与二维码类似，是一种条码技术产品，但彩码具有更鲜艳的色彩，例如，ColorZip Media研发的ColorCode具有4种颜色[14]，微软公司开发的一种大容量彩色条形码(High Capacity Color Barcode, HCCB)具有更多的颜色，可以容纳更多的信息。基于此，本文提出一种将相位加密与彩码原理相结合的光学图像加密方法。

1 理论分析

1.1 彩码的生成规则

彩码的生成规则与二维码类似，二维码中搭载的信息由一串二进制数表示，体现在二维码中，是黑白两色的方块，黑色代表“1”，白色代表“0”。而彩码则有多种颜色，文献[14]提出的彩码生成规则中，黄色代表二进制值“00”，绿色代表“01”，红色代表“10”，黑色代表“11”。微软公司提出的HCCB颜色范围则扩展到16色。在本文提出的方法中，彩码颜色与数值对应如表1所示。

图像在计算机中可以转换为由“0”和“1”表示的二进制数据，本文将原始图像的二进制文件信息依据表1生成彩码，然后将彩码用于图像加密。原始图像的恢复是通过读取彩码中的信息生成1个二进制文件完成，该二进制文件为图片文件，修改该文件后缀名即可得到恢复图像。实际上，这种转换也可看作是一种加密方式，需要知道彩码颜色相对应的信息才能正确读取彩码的信息。采用本文方法生成的彩码图片及原始图片如图1所示。

表1 彩码颜色与数值对应表

图1 原始图片与生成的彩码

1.2 Arnold变换

利用Arnold变换可以对图像中的像素点进行置乱，以达到加密的效果。Arnold变换的公式为：

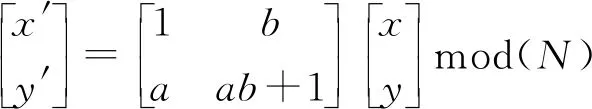
(1)

式中，a，b，N为正整数，当图像的长与宽相等时，N为图像的宽，mod表示取模运算，x，y，x′，y′分别为像素点置乱前后的坐标。将彩码作为Arnold变换的对象时，x，y，x′，y′分别为彩码各个色块的坐标，从而达到使Arnold变换对彩码信息进行置乱加密的效果，密钥是置乱次数。

1.3 纯相位光学图像加密

纯相位光学图像加密是一种仅使用光的相位信息进行加密的方法。首先将原始图像转换为相位信息，然后使用一个随机相位板对其进行加密。设原始图像为O(j,k)，其中j，k表示图像的像素点坐标，其生成的相位板为OPM(j,k)=exp[i2πO(j,k)]，其中i表示虚部。使用随机相位板R(j,k)=exp[i2πr(j,k)]对原始图像进行加密，加密结果为：

(2)

解密时，需要使用R(j,k)的共轭相位板R*(j,k)，解密过程表示为：

(3)

为了使彩码作为纯相位光学加密方法的输入图像，依照表2将彩码与相位进行转换，得到用于纯相位加密方法的相位板。彩码颜色与相位的对应关系如表2所示。

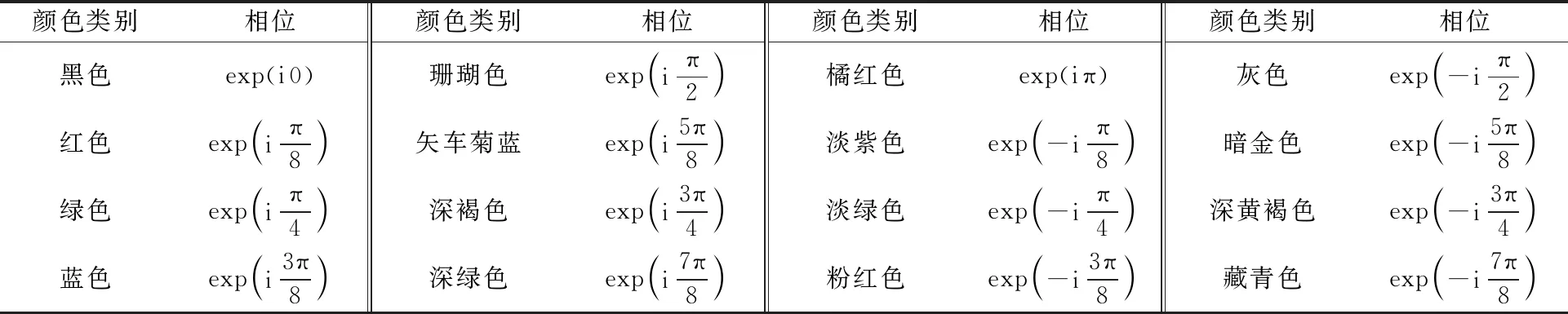
表2 彩码颜色与相位的对应关系

2 加密和解密过程

2.1 加密过程

首先，将原始图片A依照彩码生成规则生成相应的彩码I(x,y)，x，y表示彩码的色块坐标而非像素点坐标。然后将彩码进行Arnold置乱，将置乱后的彩码根据表2进行颜色与相位信息之间的转换，得到用于加密的相位板C(x,y)。使用随机相位板R(x,y)对相位板C(x,y)进行加密，得到加密结果X(x,y)。加密流程如图2(a)所示。

2.2 解密过程

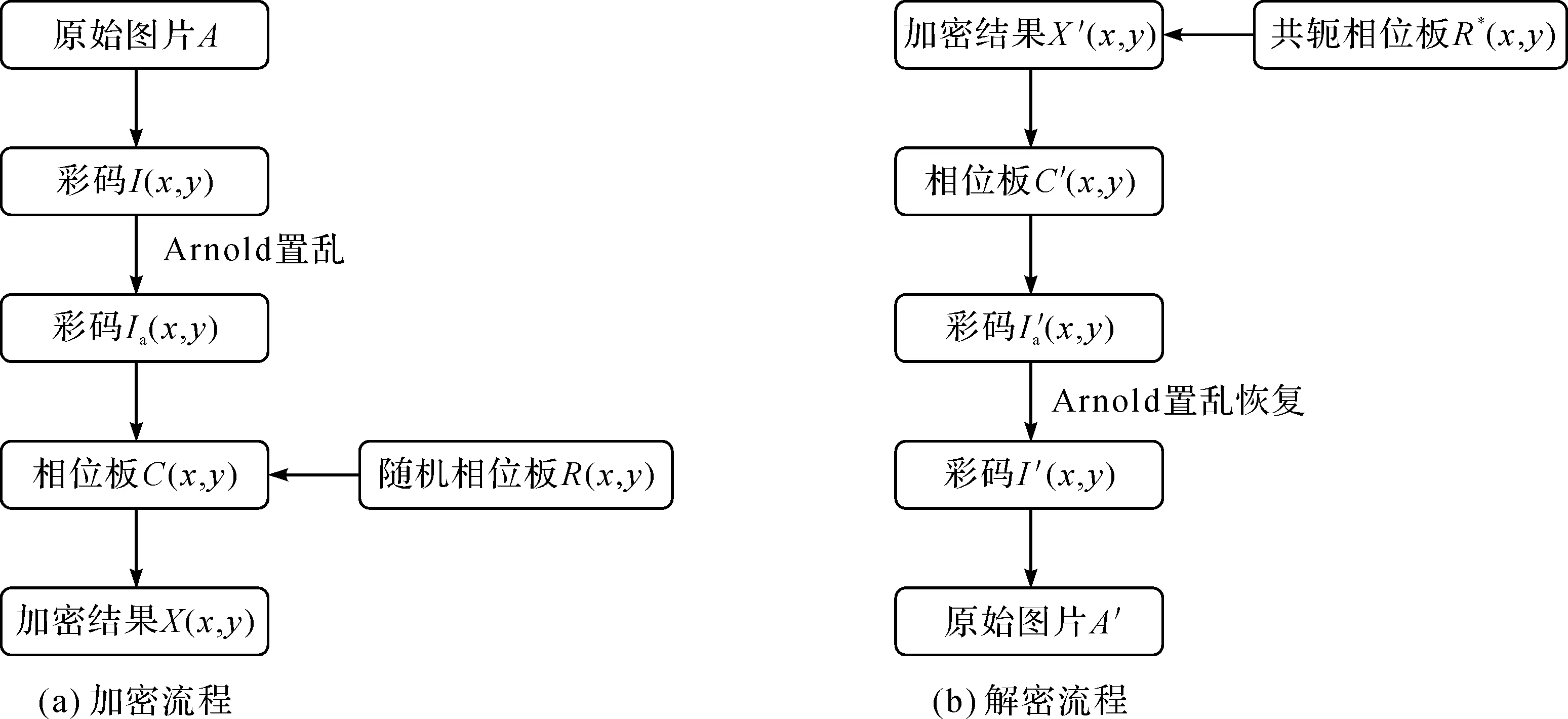
图2 加密和解密流程

3 数值模拟

本文使用MATLAB R2018b软件进行数值模拟实验。原图与生成的彩码见图1，置乱后的彩码Ia(x,y)、加密结果X(x,y)的相位分布以及解密结果A′如图3所示。原图由彩色图像生成彩码后，通过置乱以及相位加密被加密为一幅复振幅图像，由于复振幅图像无法显示，因此本文展示的是加密结果的相位分布，显示为一幅灰度图像。实际上由于加密过程中只有相位的参与，解密时只需要复振幅图像的相位信息即可完成解密。

图3 加密结果与解密结果

使用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)来评判图像的恢复效果，其计算公式为：

(4)

式中，n为每个像素的比特数，eMSE为原始图像与恢复图像之间的均方误差(Mean-Square Error, MSE)，其计算公式为：

(5)

式中，H，L表示图像的大小，A(j,k)，A′(j,k)表示原始图像与恢复图像。经过计算后得出原始图像与恢复图像之间的PSNR值为无穷大，表明本文方法具有良好的恢复效果。因为采用本文方法得到的恢复图像每个像素点上的值都与原始图像相等，这是由于原始图像的信息被完全储存在彩码中，原始图像可以被完全恢复。但是，正是因为这个特性，本文方法无法抵御剪切攻击，同时，使用错误的密钥也无法将图像恢复。

图像的直方图显示了像素值的分布信息，对加密结果进行直方图分析可以定量推断出加密方法应对统计攻击的抵御能力。原始图像和彩码的各个色面的直方图分布见图4，对比二者可以发现，彩码的直方图分布更加均匀，因此将图像转为彩码也可取得一定的加密效果。

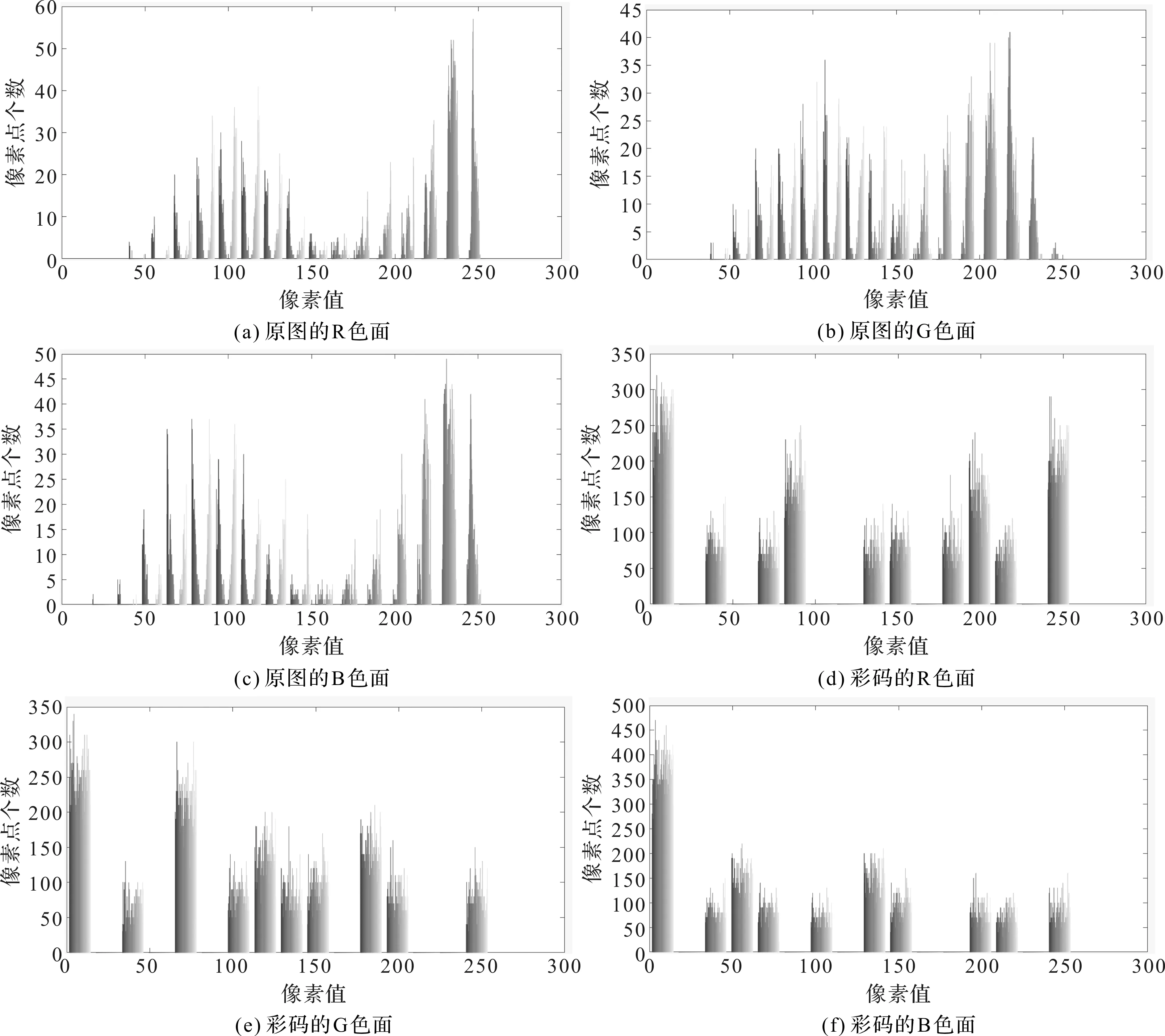
图4 原图与彩码的各色面直方图

图像因为相邻像素之间具有很强的相关性，容易受到攻击，加密结果的相邻像素相关性分析被广泛应用于加密方法的评价中。相关系数的表达式为：

(6)

式中，p，q为相邻像素值，cov(p,q)为p，q的协方差，D(p)，D(q)为p，q的方差，表达式分别为：

(7)

(8)

式中，M为选取的像素点个数，E(p)，E(q)为p，q的期望，表达式为：

(9)

本文从原始图像及密文图像中随机抽取1 000组相邻像素进行分析，计算结果如表3所示。图5展示了原始图像与密文图像在水平、垂直和对角方向上的相邻像素相关性分析。从表3和图5中可以看出，原始图像在3个方向上的像素相关性非常强，而密文图像在3个方向上的像素相关性都十分弱。

表3 原始图像与密文图像的相邻像素相关性

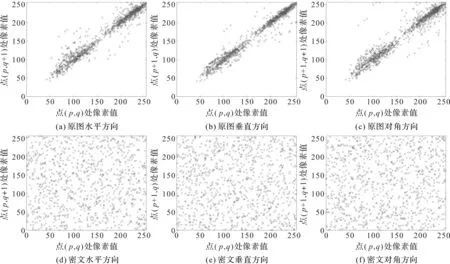
图5 原始图像与密文图像的相邻像素相关性分析

4 结束语

本文提出了一种基于纯相位加密和Arnold变换的彩码加密方法。将原始图像编码为彩码不仅可以帮助达到良好的恢复效果，还可以作为一种加密手段，拓宽加密方法的密钥空间。Arnold变换和彩码的结合提高了加密的安全性。但是，本文提出的加密方法不能抵御剪切攻击，如何将彩码与光学加密技术更好地结合，提出安全性更高的加密方法是今后的研究重点。