基于仅光学观测的短弧关联分析方法
2021-06-23姜平张雅声陶雪峰徐灿方宇强李智王浩
姜平,张雅声,陶雪峰,徐灿,方宇强,李智,王浩
航天工程大学,北京 101400
观测弧段的关联性检测是空间目标态势感知中的一个重要领域,而地基空间目标监视系统(GEODSS)在其中扮演着重要的角色。由于雷达天线的射程能力有限,近地轨道以外的空间非合作目标的绝大多数观测都是由光学望远镜进行的。根据美国国家航空航天局(NASA)的最新数据显示[1],截至2020年4月,美国空间监视网共编目空间目标(通常大于10 cm)20 437个,其中包括5 645个在轨航天器、14 792个火箭箭体和碎片。随着火箭运载能力的提升,空间在轨目标和空间碎片的数量将会大幅提升,这将会给整个空间目标监视网络带来前所未有的压力。广角望远镜的观测大部分属于“短弧观测”(短弧目前没有明确的定义,文中将相对于整个轨道周期观测时长占比不到1%的数据称为“短弧观测”),短弧观测数据对于轨道确定提出了更高的要求。若能充分利用不同观测位置、不同观测时段的数据[2],进行观测弧段的关联性检测,充分融合具有关联性的观测信息,这将极大地提升对于空间目标识别和状态估计的准确性。
光学传感器测量只能给出跟时间相关的“角度观测序列”(通常是赤经/赤纬,也可以是方位角/高度角),是无法获得距离和距离变率上的有效信息的,对于短弧数据来说无法进行有效的轨道确定,这也反映出了光学定轨对于关联的需求。文献[3-4]在开普勒轨道积分的基础上,从轨道六要素中分离出与能量和角动量无关的状态量(近地点幅角和真近点角),计算衡量相关性条件差异的目标函数,从而判断弧段之间的关联性,但其在天顶观测和共面观测的时候无法使用[5]。目前大部分的关联方式,还是从“容许域”的概念[6-7]出发,构建空间目标的距离和距离变率上的约束。文献[8]在研究地球轨道空间目标的光学相关性时,创新性地提出了将容许域映射到一个新的庞加莱元素空间,传播到同一时刻并投影到三个二维平面中,通过分析二维区域中点的相交情况来判断轨道的相关性。文献[9-10]将弧段关联问题和轨道确定问题融合在一起,给定一个初始状态,可以通过贝叶斯理论给出两个短弧段存在关联性的后验概率密度,通过最大化后验概率密度来给出使得弧段具有最强关联性的轨道。文献[11-13]引入了一种基于微分代数(DA)的新方法,该方法同样建立在容许域的基础上,利用DA估计不确定度范围来区分相关和不相关的观测值。文献[14]也对传统的初值方法进行了改进,通过搜索非奇异正则空间中定义的新损失函数的全局最小值来判断关联性。文献[15]创新性地提出了一种用于关联的几何方法,调整其中一个轨道的半长轴,使两个弧段在中间点的位置差最小化,通过半长轴的调整是否具有收敛性来判断弧段之间的关联性。文献[16]在研究天基短弧关联时提出了一种正弦拟合的关联算法。文献[17]的研究中,尝试将光学轨迹关联方法与用于大数据问题的聚类方法相结合来解决多目标轨迹关联问题。其创新性的方法也为后续的弧段关联的研究提供了开阔的思路。
目前的方法对于短弧关联性判别的效率有待提升,且判别的准确度不高。本文以“容许域”为基础,从误差分析理论出发,建立观测误差传播模型,并以角度均方误差为优化目标,充分分析了容许域中的角度误差分布特性。针对误差分布呈现的多极值点特性,采用多点优化的方式,给出容许域中“角度均方误差”的最小优化值。最后融合测角传播误差和测角固有误差,给出关联性判别的误差限,并对最终的优化结果进行统计学分析,用卡方检验的方式给出测角弧段具有关联性的判别依据。针对关联分析方法应用在LEO轨道上的困难,提出了用误差方向性判断的方法,实验结果证明改进的方法在LEO数据关联上有很好的效果。
1 基于容许域的关联性概述
基于仅测角信息的短弧关联方法,目前应用比较广泛的还是基于容许域的初值法和边值法的关联方式。但是基于容许域的方法存在本质上的不足,容许域是直接应用真实测角数据集建立的,没有考虑测量中的误差。本文提出了一种融合测角误差的短弧关联方式,在深入考虑非线性误差传播的情况下,可以根据设定的误差限进行关联性的判别。
1.1 关联方式概述
容许域的关联思路是简单直接的,即在满足第一段观测弧数据的大量轨道中,是否能够找到与另一段观测数据最小二乘拟合误差最小的轨道。当充分考虑测量误差的时候,最小二乘拟合误差就必然有一个合理的限制范围,在这个范围内,可以对关联的可信度进行进一步的评估。
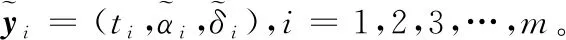
假定观测误差服从高斯分布传感器的视线误差设为σ,则根据赤经赤纬的误差几何关系,可以得到赤经赤纬具有如下统计特性:

其中预测序列与真实观测序列差的平方和表示两段观测弧段之间的关联性大小:
由此可以定义观测序列角度误差的均方根误差,用来表征观测序列和预测序列之间的平均误差,简称“角度均方误差”:
式(3)可以视为对于赤经赤纬误差的平均误差,通过优化平均误差来找到使得观测弧段之间拟合效果最好的轨道,这样就将短弧关联问题转化为以平均误差为优化目标的参数估计问题。判断短弧段之间是否存在相关性,还需要一个合理的误差限进行判断。误差限的确定要充分考虑预测序列和真实测量序列中的误差,真实测量序列中的误差是传感器的测量噪声,预测信息的误差计算方法将在第1.2小节中进行详细叙述。
1.2 预测信息的误差计算
不难发现,当分析预测序列和实际观察序列之间的误差时,预测值的误差可以通过对传感器视线误差进行非线性传播得到[19]。光学测量的不确定性传播算法,包括高斯混合模型(GMM)[20-21]、状态转换张量(STT)[22]、多项式混沌(PC)[23]、基于自适应熵的分割方法[24]等。但是这些方法都需要复杂的计算。为了降低复杂度,提升关联的效率,本文考虑使用泰勒展开提取一阶近似项进行线性化的方法,并用蒙特卡罗方法证明了短弧上线性传播方法的准确性和合理性。
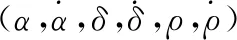
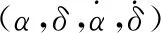
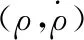
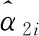
令:
f0=
这样通过泰勒级数展开建立非线性函数的线性关系表示:
用Taylor级数的形式可以准确地描述非线性函数中的误差传递关系,对于足够小的误差和较小的观测序列曲率,Taylor级数中的高阶项影响可以忽略不计。当有数据呈现高曲率或误差不确定性较大时,泰勒级数的线性近似性就会很差,需要考虑高阶项的影响。对于本文中短弧段的关联,观测序列曲率不会很大,用一阶项可以很好地近似。
图1 赤经赤纬误差分布

式中:xi为采样点;K(·)为核函数(这里选取的核函数为Gaussian函数);h为窗口宽度。
从图1可以看出,通过两个方法获得的角度误差密度曲线基本吻合。如表1所示,给出由蒙特卡洛法和误差传播模型得到的赤经赤纬的协方差计算值,其结果计算的差异度小于5%,从而充分证明了误差传播模型的理论正确性。
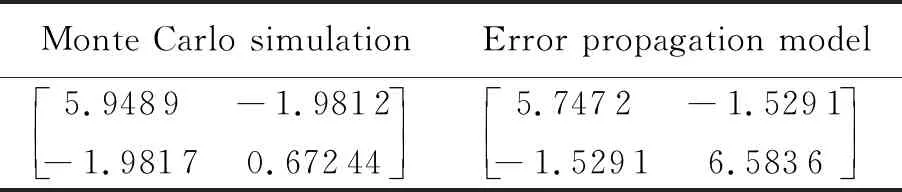
表1 蒙特卡洛和误差模型传播协方差计算结果
2 基于卡方检验的关联性分析
2.1 容许域轨道采样
首先,通过二体轨道的能量约束,最小能量约束和远近地点约束,对距离和距离变率进行约束,构建完整的容许域可行解区域。在容许域中进行轨道采样,获得的采样点如图2中阴影部分所示,其中每一个采样点都可以代表一条轨道。
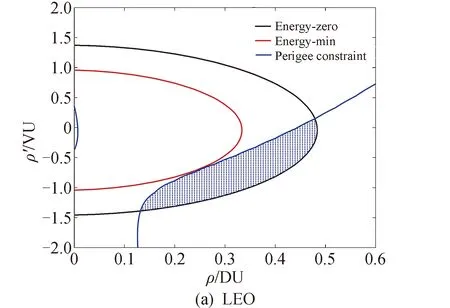
图2 容许域
图2中距离和距离变率表示,采用归一化单位,分别以DU=6 378.136 6 km和VU=7.905 365 96 km/s作为单位长度和单位变化率。
得到“容许域采样轨道”后,就需要将其传播到需要进行关联的另一个观测弧段的观测时刻进行“角度均方误差”的计算。图3显示了一颗低轨卫星的误差计算结果,从图3(a)中可以看出,误差呈现出“多极值点”的分布特性,图3(b)中显示出给定某一误差值后的轨道分布特性。“多极值点”特性的存在主要是因为两个待关联弧段的长时间间隔,会引起轨道转数(卫星运行完整轨道周期的次数)的不确定性,都可能使得待关联弧段之间的“角度均方误差值”达到极小,在对低轨卫星关联时,这种特性表现的尤为明显。众多极小值的存在,给优化过程带来了极大的困难。
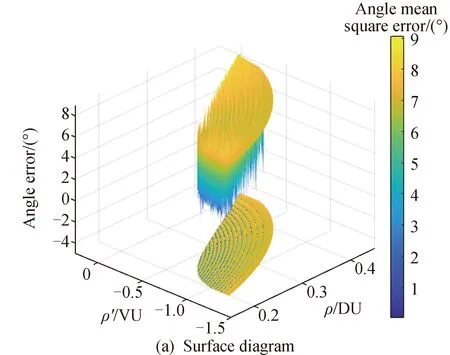
图3 LEO卫星角度均方误差
为了找到拟合两段观测弧段的最佳轨道,初步采用在容许域中进行“多点优化”的方式。通过对采样轨道“角度均方误差”的计算,可以确定出能够使两段观测具有最强相关性的候选轨道。候选轨道的筛选是从采样轨道中选取出能够使得“角度均方误差”最小的一部分点。候选轨道如图4所示,由红色点标出,图4(a)(b)(c)分别给出了两个观测弧段属于同一低轨卫星、两个观测弧段属于同一高轨卫星,以及两个观测弧段属于不同卫星的情况。
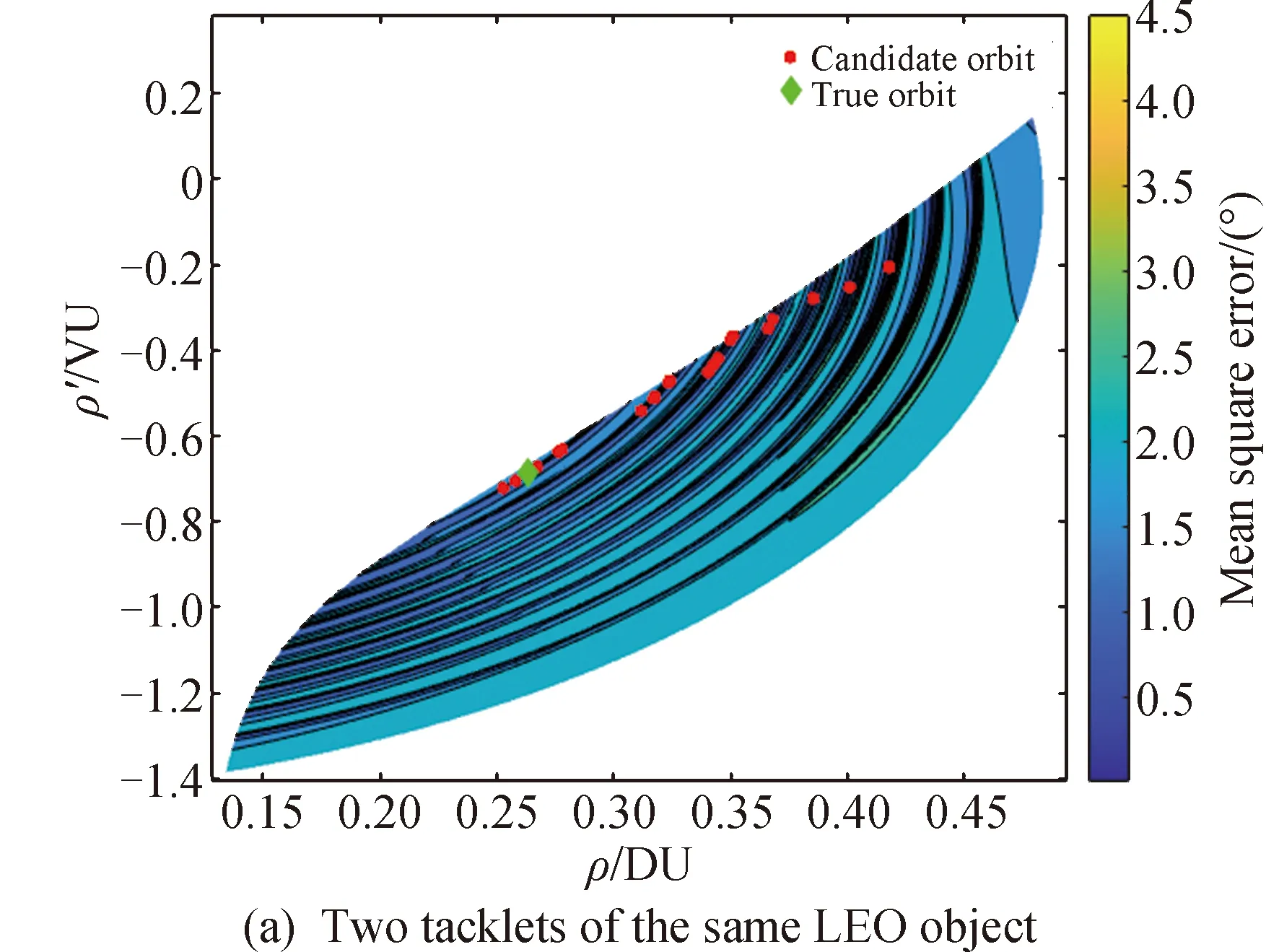
图4 利用角度均方误差进行候选轨道筛选
从图4可以明显看出,在对相关弧段和不相关弧段的“角度均方误差”计算中,相关与否并没有在容许域中表现出来明显的差异。也就是说,即便是不相关弧段,仍旧可以找到将两个弧段拟合得很好的一条轨道。所以就需要能够给出判别关联与否更细致的标准,具体关联的标准将在第2.3小节中给出。
2.2 候选轨道的“角度均方误差”的优化
合理的初值对优化问题的解决是非常重要的,在第2.1小节中,利用容许域采样到了非常接近于真实轨道的优化初值。这里继续对获得的“候选轨道”进行角度均方差优化,具体的优化算法可以采用解决非线性最小二乘问题的Levenberg-Marquardt(LM)算法等。如图5所示,对于相关弧段和不相关弧段,迭代的优化值存在明显的收敛和不收敛特性。从曲线的收敛性上,可以给出相关与否的定性判断,即具备相关性的弧段在优化过程中存在明显的收敛特性,不具备相关性的弧段在优化过程中没有收敛特性。
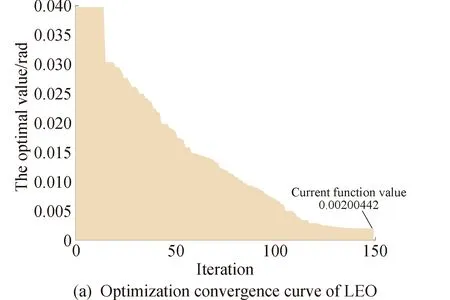
图5 角度均方误差的优化收敛特性
对于前两节中给出的定性判断相关性的方法在对不同轨道上的仅测角弧段中已经得到了充分的验证。对于收敛到的“角度均方误差”有多大的可能性判断两个观测弧段存在真实的相关性,还需要进行详细的统计学分析。
2.3 基于统计学的关联性分析
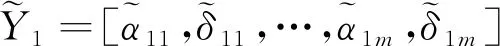

对单个随机变量进行如下变形:
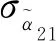
则预测值和真实测量值之间的误差平方和应该服从自由度为2n的卡方分布,所以可以多个合并为:
χ2=
(13)
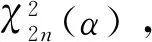
由(14)式得到上侧分位数为α的“χ2误差限”,当通过角度预报误差和传播误差计算出的卡方值小于“χ2误差限”时,可以相应做出观测弧段之间具有关联性的判断,即可以认为两个观测弧段具有内在的相关性,可能出自于同一个空间目标。同时,根据卡方分析,做出这种判断的可信性为(1-α)(通常选取α=0.01,保证空间目录不被污染的条件下,准确检验到弧段之间的关联性)。
3 仿真及验证
由于容许域的采样轨道广泛,如果在未知观测弧段是否相关的条件下,用高精度轨道模型计算,那势必会带来非常大的计算量,严重影响关联的整体效率,所以首先考虑的是,用低精度的J2模型在保证高效的计算的情况下,能否进行弧段关联的判定。
3.1 模型精度分析
在进行轨道传播时,选取的两种轨道预报模型分别为J2和HPOP轨道预报模型[27]。由于仅测角数据没有距离约束,会有大量的采样轨道进行传播,在利用HPOP模型进行预报计算的时候,会形成很大的计算量。大量的计算也会影响在实际关联中的整体效率。在图6中选取了已知具有关联性的LEO卫星的两段观测弧段,同时用J2和HPOP模型进行优化。(实验选取的LEO卫星轨道高度在1 000 km以上。)
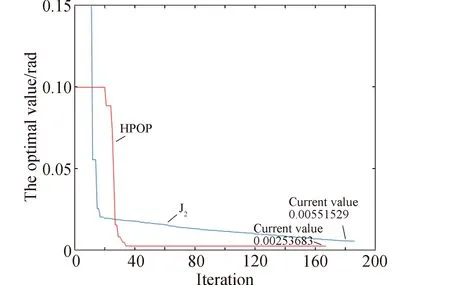
图6 LEO卫星HPOP和J2模型优化结果
对比两种模型优化的“角度均方误差”可以发现,在整体优化过程中,J2模型的优化精度已经足够了,用高精度模型进行预报的时候并不会带来量级上的提升。所以在实际应用中使用J2模型进行关联应该是可行的,这不仅会提升计算效率,而且也具有足够的可信性。
3.2 不同类型轨道的关联检验
本文拟使用5个半长轴和偏心率不同的在轨空间目标检验短弧关联分析算法。卫星真实轨道使用TLE数据外推获得[28]。测站位置大地坐标为(109°,34°,557 m)。对于LEO、HEO、MEO、GEO的观测弧段时长分别取30 s,5 min,5 min,15 min,观测角度误差设置为3″。初步测试数据选取每个卫星上间隔超过10 h的各两段观测数据,一共10段观测数据进行关联匹配,卫星的数据参数如表2所示[29]。
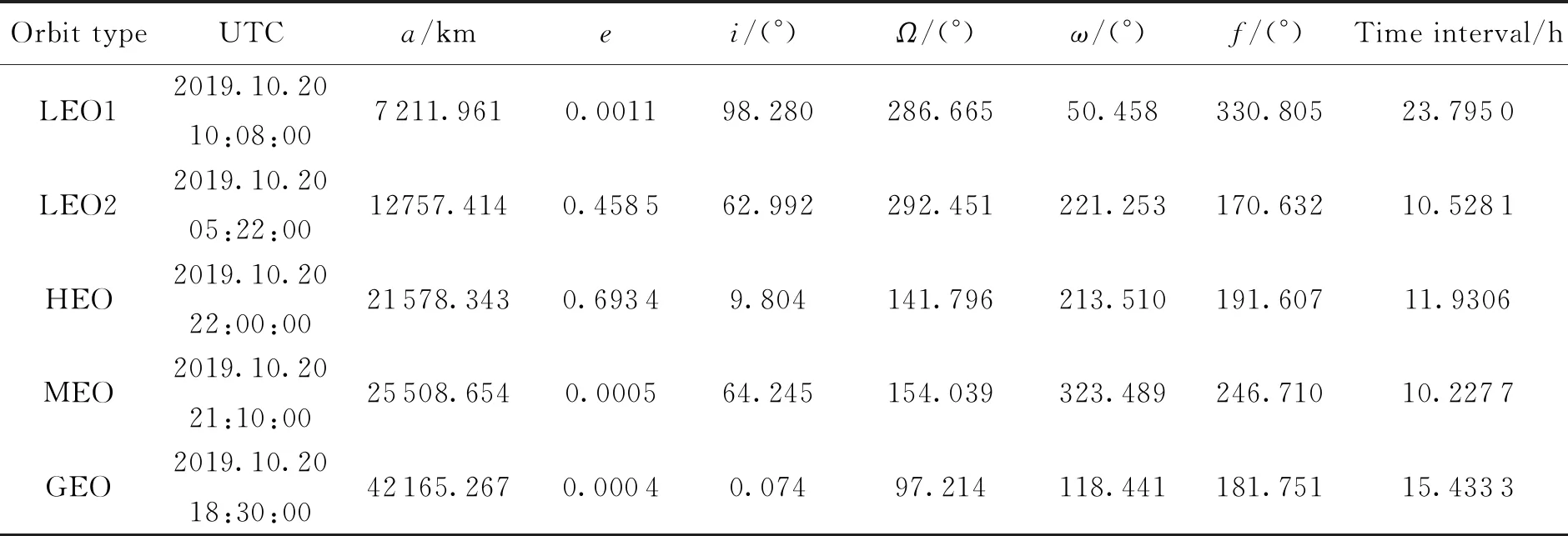
表2 实验卫星参数
为了便于比较关联和观测结果,如图7所示,将卫星的轨道投影到笛卡尔坐标系的3个平面上,用黑色点迹标出了10段观测弧段所在位置。
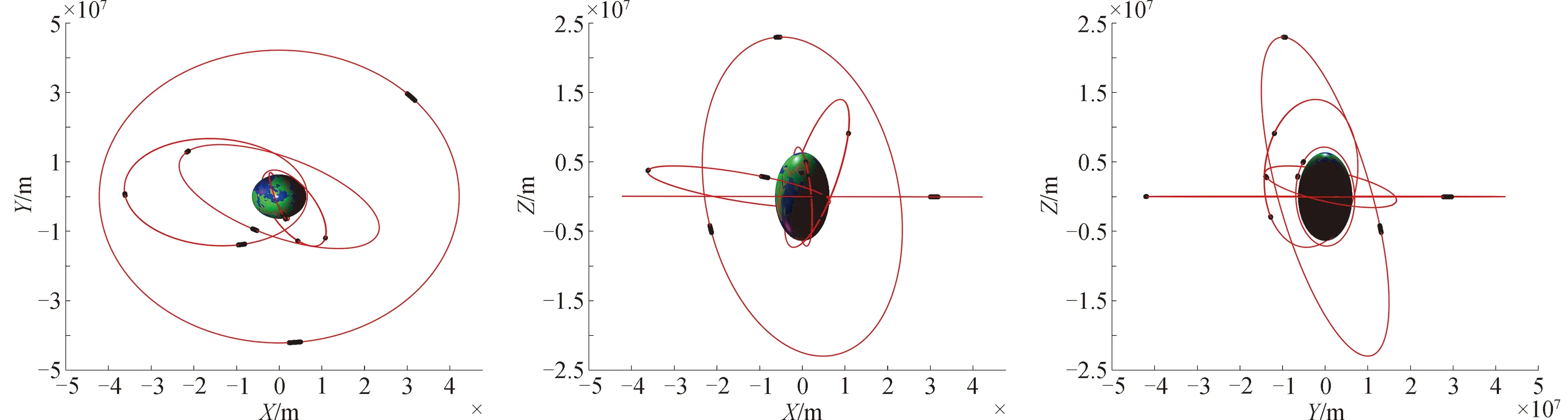
图7 测试轨道在X-Y,X-Z,Y-Z平面投影
如图8所示,给出了5条轨道上观测数据的关联结果,可以发现关联算法已成功对空间目标的观测弧段进行准确关联。
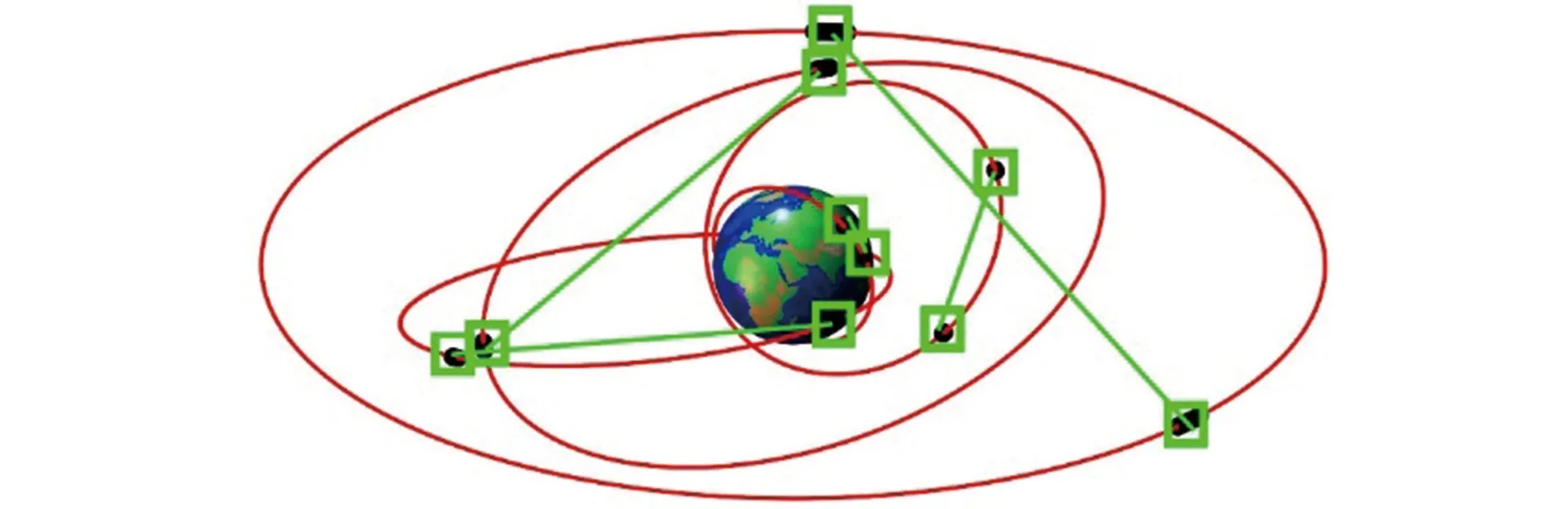
图8 测试轨道的关联匹配结果
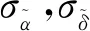
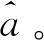
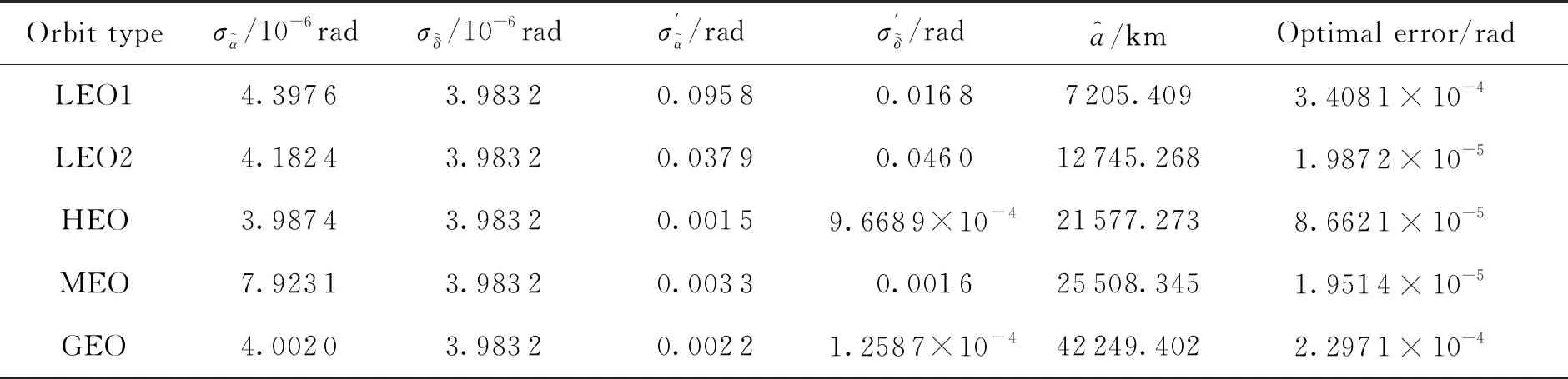
表3 关联算法验证结果
3.3 关联匹配验证
为了获取更多的观测数据进行关联性验证,在space-track中公布的卫星轨道根数数据中,根据不同轨道高度,筛选出低轨道COSMOS卫星共计44颗,中轨道SLOT卫星共计40颗,高轨道北斗GEO和IGSO轨道卫星共计17颗。为了增加关联的难度,通过STK仿真计算为每个卫星生成了3天时间内的多次观测数据,其中有部分卫星的轨道是十分相近的,这也给短弧段观测数据关联带来了极大的挑战。
在对观测数据中的任意两个进行关联时,其结果可能是以下4种情况之一:
1)True Positive(TP),两个观测弧段属于同一个目标,且关联结果认为是同一目标。
2)True Negative(TN),两个观测弧段属于同一个目标,但是关联结果认为不是同一目标。
3)False Positive(FP),两个观测弧段不属于同一个目标,但是关联结果认为是同一目标。
4)False Negative (FN),两个观测弧段不属于同一个目标,且关联结果认为不是同一目标。
其中TP和FN的比例越高,可以认为关联的正确率越高,表4中给出了实验数据的关联匹配结果。
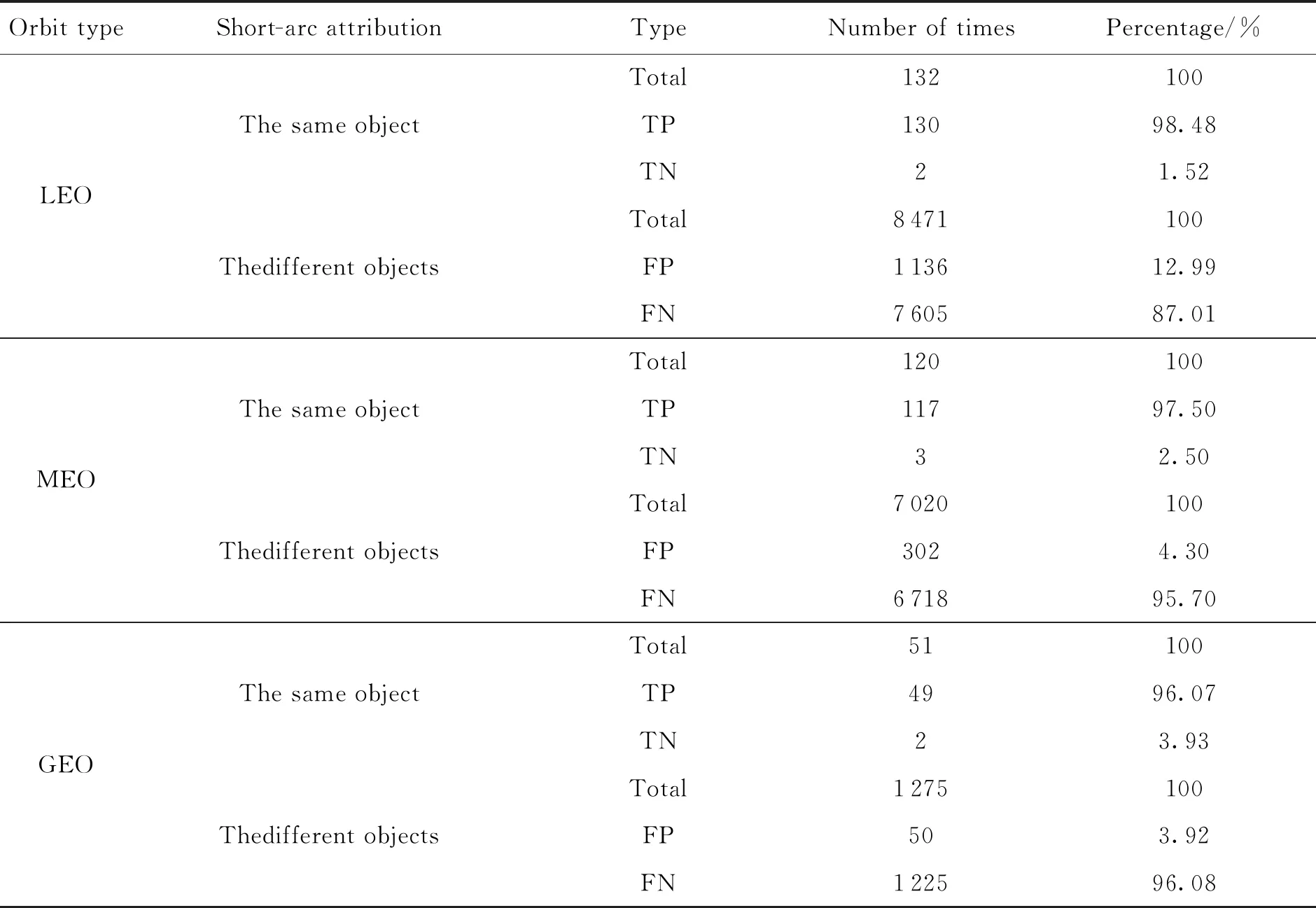
表4 短弧数据关联结果
从关联的结果上看,算法对于不同轨道的关联真正率很高,但是对于长时间间隔的数据,假负率就会变得很低,对于低轨卫星识别来说表现尤为明显。从表3中数据可以发现,对于长时间间隔的数据,低轨卫星相较于中高轨卫星的传播不确定度就会变得很大,这主要是由于低轨卫星转数很大造成的。而对于轨道很相近的卫星的观测来说,很容易找到拟合两次观测的最优轨道,其优化的误差值也很容易在接受的范围之内。所以对于长时间间隔的低轨卫星来说,利用误差不确定度来进行关联的判别,会造成一些关联的误判,而对于中高轨的数据关联,由于转数很小,关联匹配度非常高。
3.4 误匹配解决方案
由于可用信息有限,对于低轨,尤其是低轨星座等近似轨道目标进行区分的时候难度很大。美国SpaceX公司提出Starlink计划,预计将会有上万颗的低轨卫星,这将会给未来的空间目标监视系统带来巨大的压力,仅靠雷达的跟踪式探测,将不能满足监视需求,充分发挥广角望远镜监视系统的作用将会有重大的战略意义。针对第3.3小节中对于低轨卫星,用仅测角观测数据进行关联的时候,可能会发生关联性误判的情况,本小节中给出低轨近似轨道目标误匹配的解决方案。
在角度预报误差的计算过程中仅仅考虑了误差的大小,这里又详细地给出了误差的“方向性”特征。图9给出了误关联时候得出的优化轨道与真实观测数据间的(α,δ)拟合偏差,对比图10中给出正确关联时候(α,δ)的拟合偏差。

图9 误关联的角度拟合偏差
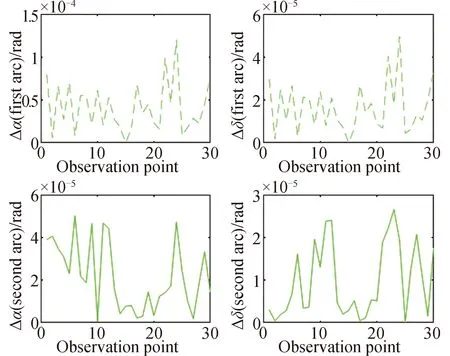
图10 正确关联的角度拟合偏差
通过分析拟合偏差可以发现对于误关联的弧段,第二段弧的拟合偏差存在明显的“V”字型特征。这主要原因是由于拟合轨道相对于真实轨道,在轨道倾角上存在明显偏差导致的。通过识别“V”字型特征可以排除其中的误关联情况的方法,表5着重对比使用误差“方向性”特征识别后,LEO数据的关联结果,从中可以看出关联的准确性有明显的提升。
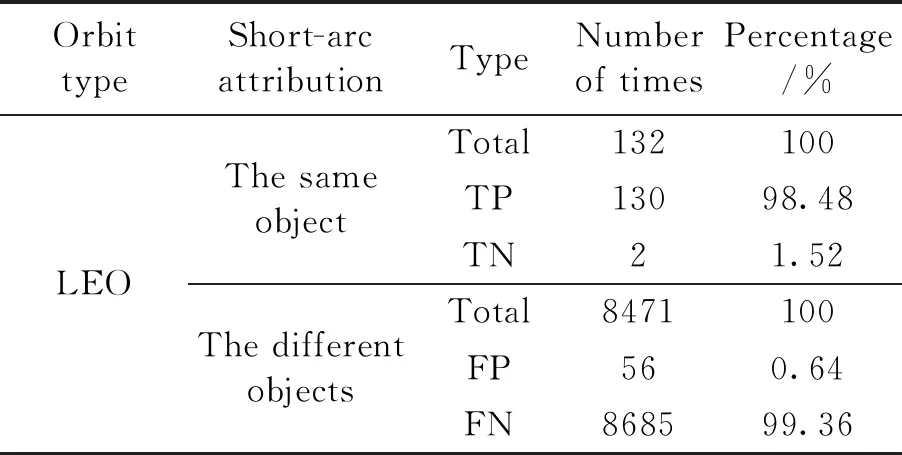
表5 数据关联结果
4 结束语
本文研究了一种判断光学仅测角弧段关联性的分析方法,对比蒙特卡洛仿真结果分析了线性化的误差传播方式在短弧观测数据关联上的可行性。这种基于容许域的方法在短弧轨道不确定的情况下,仍旧可以通过卡方分析拟合观测弧段的最优轨道,给出弧段之间具备关联性的依据。把基于容许域的关联方法应用在不同类型的轨道上进行合理性的检验,在对LEO轨道卫星的观测数据进行关联的时候,假正率很高。针对在低轨星座等近似轨道目标误关联率高的情况,根据误差方向性特征进行误关联识别的方式,可以显著提升光学仅测角弧段关联的准确性。
利用容许域进行关联有很好的应用前景,本文在短弧观测无法进行初轨确定的情况下,给出了光学观测弧段关联的稳定方法,并显著提升了对于LEO轨道光学观测关联的成功率。本文的研究可以为空间目标编目和后续的精密轨道确定提供数据支撑。
