一种基于多虚拟观测量的组合导航自主完好性监测方法

吴孔阳， 叶小舟，肖伟，刘文祥，刘小汇

国防科技大学 电子科学学院，长沙 410073

全球卫星导航系统信号容易受到电磁干扰、树林遮挡及多径效应影响，对系统完好性构成严重威胁，尤其对安全性能要求较高的航空用户，其造成的后果可能是灾难性的[1]。考虑到系统建设成本及便利性，对于完好性监测的研究主要集中在接收机自主完好性监测技术上[2],用于提供水平方向的完好性监视[3]。RAIM通过冗余测距信息的一致性校验实现用户接收机对故障的检测，并在给定时间内向用户告警[4]。目前，国内外学者针对RAIM技术设计了快照法进行故障检测，主要包括奇偶矢量法[5]、最小二乘法[6]，对于伪距阶跃故障有较好的检测性能[7]，但是对微小伪距偏差故障检测概率较低。文献[8]中提出一种多历元积累检测量的故障检测方法，但是当伪距偏差符号未知时会对算法的检测性能造成影响。文献[9]提出了一种非相干积累的微小伪距偏差检测法，通过构造非相干检测量消除了伪距偏差符号对故障检测性能的影响，但是算法对可见星不少于5颗的要求在一定程度上限制了算法的使用。基于钟差辅助[10-11]、气压计辅助[12-13]的算法，通过建立简单的钟差预测模型或高度预测模型，在4颗可见星的条件下即可进行故障检测。

此外，由于INS与GNSS系统的互补特性，两者结合的组合导航系统受到广泛研究，其中组合导航的卡尔曼新息检测法[14-15]被用于组合导航的完好性监测。该方法不仅可以检测故障，而且还能识别故障，但是计算量大，需要系统模型的先验信息且算法性能对模型误差敏感[16]。

本文提出一种INS辅助的RAIM方法，通过INS输出的位置构造与可见卫星中的1颗卫星视线方向相互垂直的2颗虚拟卫星，通过虚拟卫星的虚拟伪距观测量扩展出新的伪距观测方程，增加了系统信息冗余度。考虑到不同卫星伪距测量误差及INS误差的异方差性，通过加权最小二乘残差法实现对阶跃故障的检测，同时改善了几何构型。与钟差、气压计辅助相比，INS辅助提供了更多的冗余信息，2颗可见星条件下即可进行故障检测，与组合导航的卡尔曼新息检测法相比，该方法不需要过多的先验信息，对模型误差不敏感，更具有实用性。最后通过实测数据验证了INS辅助的加权最小二乘算法的性能，而且仿真分析了不同INS精度等级下对该方法故障检测性能的影响。

1 RAIM算法

1.1 加权最小二乘算法

最小二乘RAIM法是在伪距比较法的基础上应用最小二乘原理进行的批量式求解方法。其GNSS线性化伪距测量方程组为：

y=Hx+Aε

(1)

假设有n颗可见卫星，其中y为n×1观测伪距与估计伪距之差；H为n×4维的观测矩阵，由各颗可见卫星到用户接收机的方向余弦向量与第4列均为1的元素构成的伪距线性化矩阵；x为4×1维向量，由用户接收机真实坐标与估计坐标之差和接收机钟差组成；A为n×n维的权值矩阵，其非对角元素为0，对角元素为测距误差的标准差σi；ε为n×1维矩阵，εi～N(0,1)。

考虑到不同卫星的信号通过的大气仰角不同，伪距测量误差也应该是不同的[17]。与最小二乘法(least squares, LS)相比,加权最小二乘法(weighted least squares, WLS)考虑到了卫星导航系统中多种误差源对故障检测的影响，通过这些误差的方差和的倒数作为加权因子来平衡多种误差源对不同卫星的影响，与最小二乘法相比拥有更好的故障检测性能[18]。

通过对式(1)求加权最小二乘解

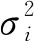
相应的伪距残差vWLS为：

式中：SWLS=(In-H(HTWH)-1HTW)，通过式(3)的伪距残差得到伪距残差加权平方和SSEWLS，即：

根据矩阵SWLS的定义，式(4)可以等效为：

可以通过二元假设，来对应系统中是否存在故障：

H0:无故障星，SSEWLS～χ2(n-4)。

H1:存在故障星，SSEWLS～χ2(n-4，λ)，λ为非中心参数。

根据SSEWLS的统计特性可以构造检测统计量：

给定虚警概率PFA的条件下，可以求得故障检测门限[19]：

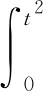
(7)

1.2 INS辅助RAIM方法

INS辅助的完好性检测方法是利用惯性导航系统不受电磁干扰的影响[20]并且能够提供接收机的位置、速度的参考信息的特点，主要原理是：通过INS输出的位置信息和构造与可见卫星中的1颗卫星(如：仰角最大的j星)视线方向相互垂直的2颗虚拟可见卫星，然后将INS位置信息与j星以及2颗虚拟卫星位置信息构造3个虚拟的卫星伪距观测量，充分利用了INS的三维位置信息，以此提供冗余的伪距观测信息与卫星观测矩阵扩展来进行故障检测。与钟差辅助、气压计辅助等方法相比，INS辅助能够提供更多的冗余信息，不仅可以提高故障检测概率，而且2颗星即可进行故障检测，提高算法的可用性。算法流程见图1。

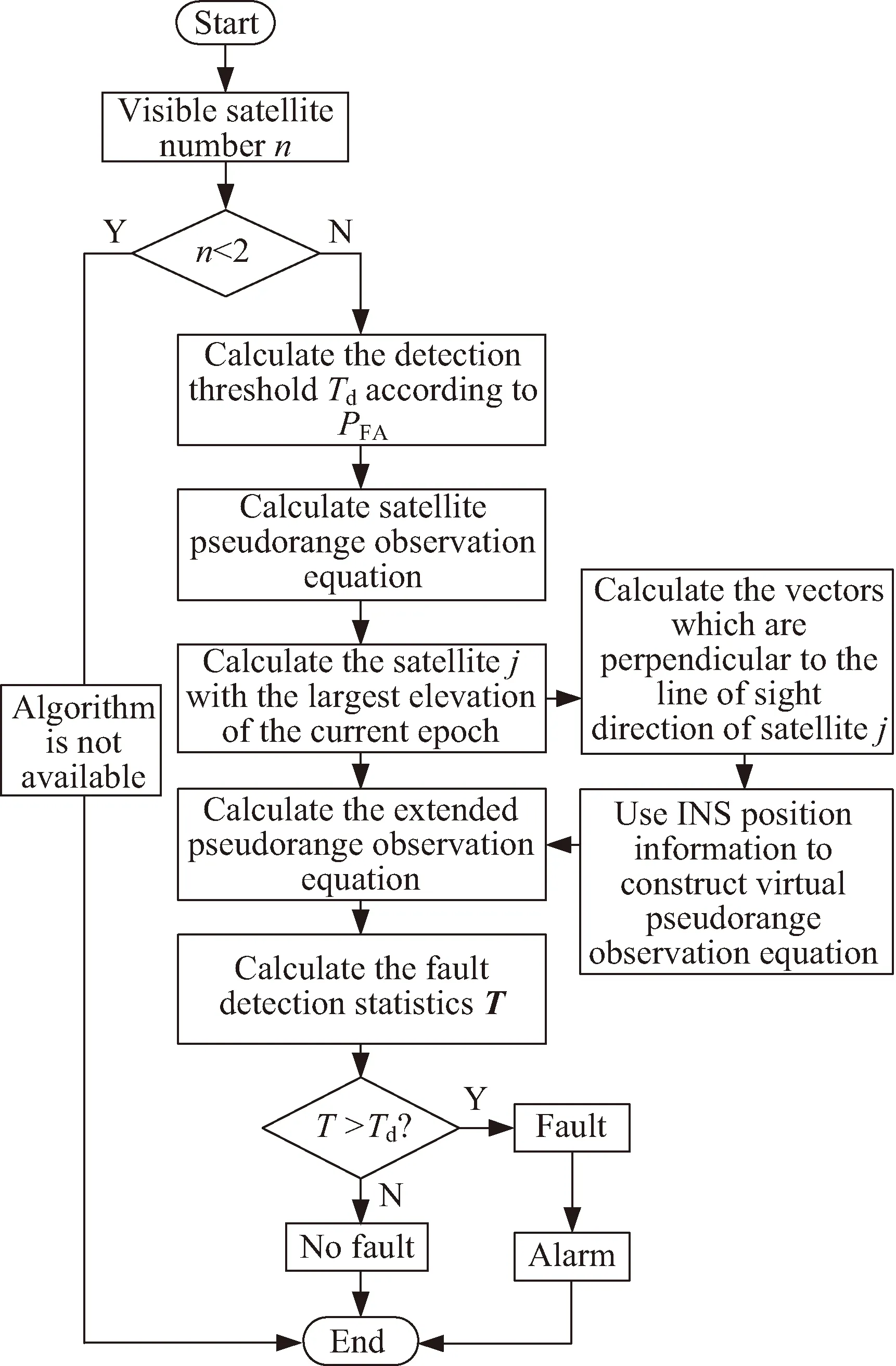
图1 INS辅助故障检测流程

假设当前观测历元共有n颗可见卫星，根据该思路，若经惯导解算后在ECEF坐标系下的INS输出位置为XINS=(xI,yI,zI)，然后可以根据星历信息和接收机的测距信息计算得到卫星的位置，再通过几何关系构造与n颗可见星中仰角最大的j星方向向量相互垂直的2颗虚拟卫星的位置，记为Xv1=(xv1,yv1,zv1)，Xv2=(xv2,yv2,zv2)，可得INS对应的j星及2颗虚拟卫星的虚拟伪距为：

其中(xs,ys,zs)为与INS构造虚拟伪距的卫星位置。假设INS输出的位置与接收机真实位置存在误差项(εx,εy,εz)，在设计良好的组合导航系统中，INS位置得到实时的校正，那么INS传感器噪声将是造成定位误差最大的噪声源，而在大于1 s的较大的时间尺上，INS传感器噪声可以视为白噪声。

对式(8)INS虚拟伪距线性化展开之后：

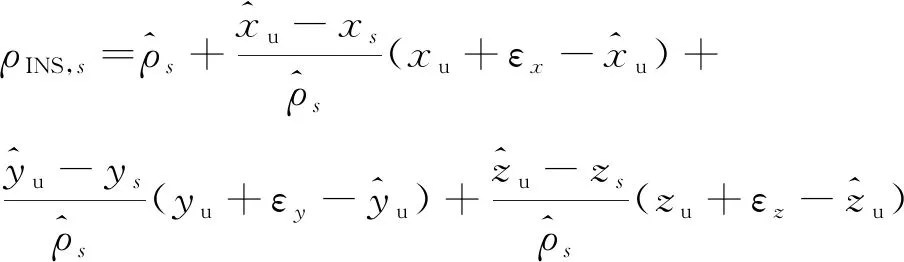
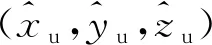
由式(9)可得：

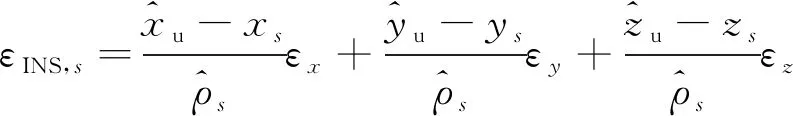
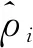
则INS辅助下的伪距观测方程扩展为：

由于卫星测距误差与INS虚拟伪距误差之间均不相关，Cov(εi,εj)=0，Cov(εi,εINS,j)=0,同时构造的虚拟观测量之间的卫星方向矢量相互垂直，因此认为虚拟观测误差之间不相关，即：Cov(εINS,i,εINS,j)=0,则将加入INS辅助后的扩展伪距观测方程(13)同样记为：

Y=GX+Bε

(14)

式中：Y为(n+3)×1维测量伪距与估计伪距之差；G为(n+3)×4维的观测矩阵，由于INS中不存在钟差项，所以在观测矩阵对应的钟差位置元素为0；X为4×1维的位置差与钟差向量；B为(n+3)×(n+3)维的测距误差权值矩阵，其非对角线元素为0，对角线元素为对应的测距误差的标准差；ε为(n+3)×1维的服从标准正态分布的误差向量。

由上述可得式(14)的加权最小二乘解XWLS为：

XWLS=(GTWG)GTWY

(15)

式中：W为(n+3)×(n+3)维的权值矩阵。由式(14)、(15)可知W=(B-1)2，其非对角元素为0，对角元素为测距误差方差的倒数。

由式(15)可得伪距残差vWLS为：

vWLS=Y-GXWLS=SBε

(16)

式中：S=(In-H(HTWH)-1HTW)。可得伪距残差加权平方和SSEWLS为：

SSEWLS=vWLSWvWLS=εTBWSBε

(17)

则其故障检测统计量T为：

与在恒虚警概率条件下求得的故障检测门限Td相比较，若T>Td，则存在故障星。

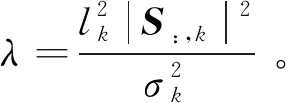
如果系统中存在故障星，那么故障检测概率Pd也是体现RAIM算法性能的重要指标之一。一般计算出故障检测门限之后，在虚警概率一定的情况下，故障检测概率只和非中心参数大小有关，根据非中心卡方概率分布函数有：

1.3 权值矩阵

由于卫星导航系统在测距过程中存在多种误差源，包括但不限于对流层误差、电离层误差、多径效应以及接收机内部热噪声引起的测距误差[21]，因而卫星测距误差方差为上述误差方差之和。

上述各其他误差方差估计如下[23]：

(1)修正的电离层误差方差

σion,i=[1-(RecosEi/(Re+hI))2]-1/2σuive

式中：Re是地球半径；Ei是第i颗卫星仰角；hI是电离层的平均高度；σuive与卫星的磁方位角φ有关[24]，具体表现为：

(2)修正的对流层误差方差

(3)修正的多径误差方差

σmp,i=0.13+0.53×e-Ei/10

由于接收机噪声引起的测距误差方差与卫星所在位置无关，因此一般可取经验值：

σnoise,i=0.1 m

在最小二乘法中并没有考虑伪距测量误差的异方差性，而加权最小二乘法通过权值矩阵给不同的测量误差方差分布不同的权值，消除测量误差的异方差性，提高故障检测算法对故障的敏感度。

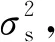
W-1=

2 仿真验证及分析

2.1 仿真验证

为了验证所提算法的性能，选用了NovAtel Span采集的2019年11月11日15:20—15:45共20 min的数据进行仿真分析，且仿真数据中不存在卫星故障情况。仿真中设置虚警概率为10-5，对于加权最小二乘RAIM算法，卫星可见数n与故障检测门限如表1所示。

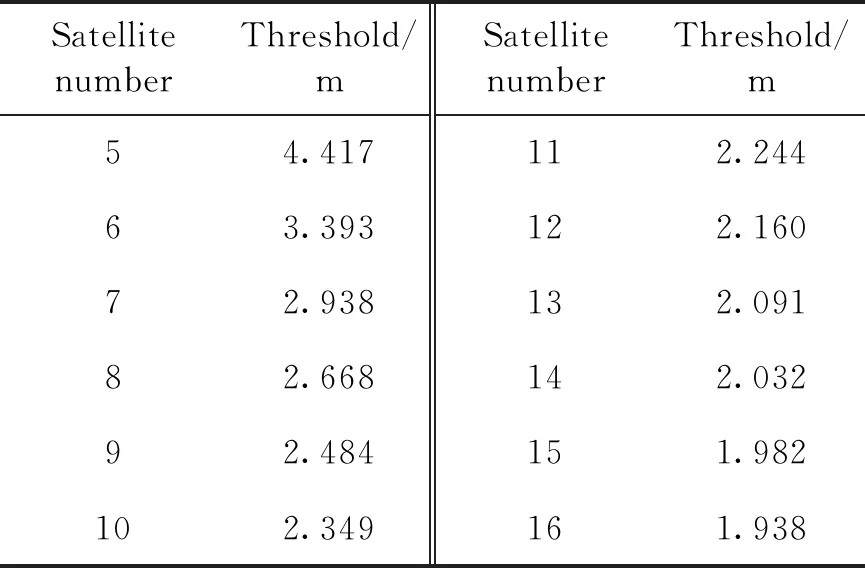
表1 加权RAIM算法可见卫星数与故障检测门限

对于INS辅助的加权最小二乘RAIM算法,可见卫星数n与故障检测门限如表2所示。

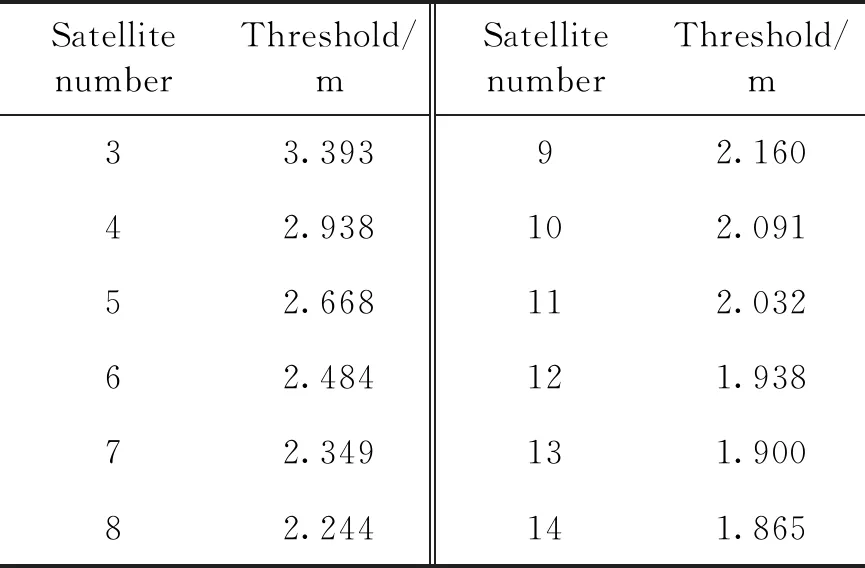
表2 INS辅助加权RAIM算法可见卫星数与故障检测门限

在故障仿真时为了便于观察试验结果，在第200历元到第300历元之间均加入了单星故障信息。然后对比分析加权最小二乘RAIM算法和INS辅助的加权最小二乘RAIM算法检测出来故障历元数，在加入35 m阶跃故障时，仿真结果如下所示。

图2和图3分别是加权最小二乘算法在加入35 m故障幅值时故障检测门限和定位误差方差的仿真结果。

图2 加权最小二乘各历元检测门限

图3 加权最小二乘定位误差

图4和图5分别是INS辅助加权最小二乘算法在INS定位误差方差σs=1条件下加入35 m故障幅值时故障检测门限和定位误差方差的仿真结果。图6为两种算法的GDOP值对比。

图4 INS辅助加权最小二乘各历元检测门限

图5 INS辅助加权最小二乘定位误差

图6 两种算法的GDOP值对比

然后为了比较最小二乘法、加权最小二乘法、INS辅助加权最小二乘法3种算法的故障检测概率，在观测数据的每个历元中均加入了单星故障信息，故障幅值为0～100 m，步长为5 m，得到3种算法的故障检测概率如图7所示。最后为了分析INS等级对故障检测概率的影响，分别选择导航级、战术级、MEMS 3种等级INS的典型值进行了仿真，性能参数如表3所示[25]。

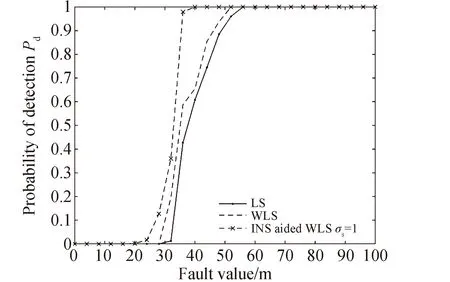
图7 不同算法故障检测概率对比

图8为INS加权辅助与卡尔曼残差法故障检测性能对比。通过表3不同INS等级的典型值，分别设置在σs=1、σs=7、σs=15的条件下仿真得出导航级、战术级、MEMS级3种INS精度等级辅助下的加权最小二乘算法的故障检测概率如图9所示。

表3 不同INS等级典型参数

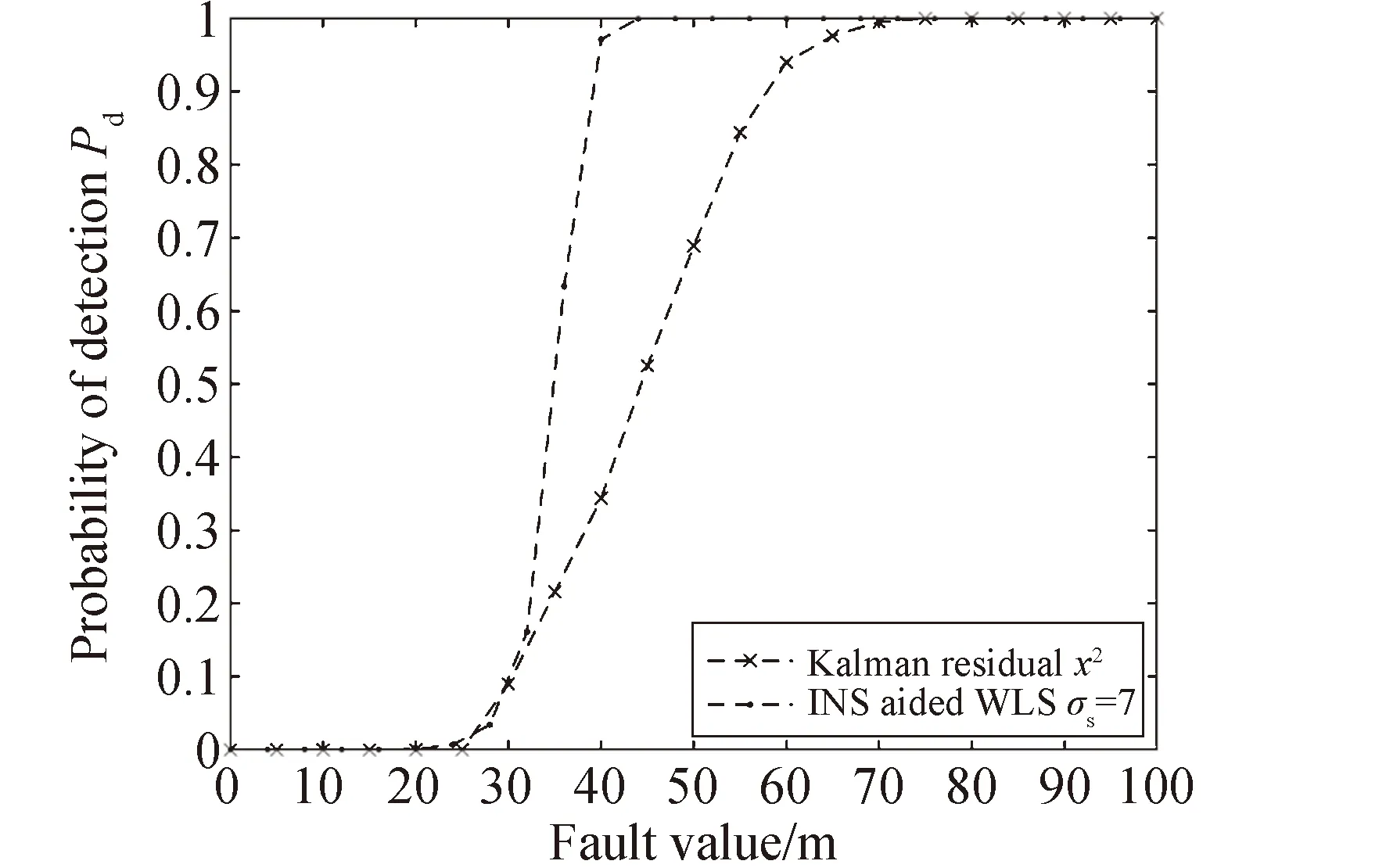
图8 INS加权辅助与卡尔曼残差法故障检测性能对比

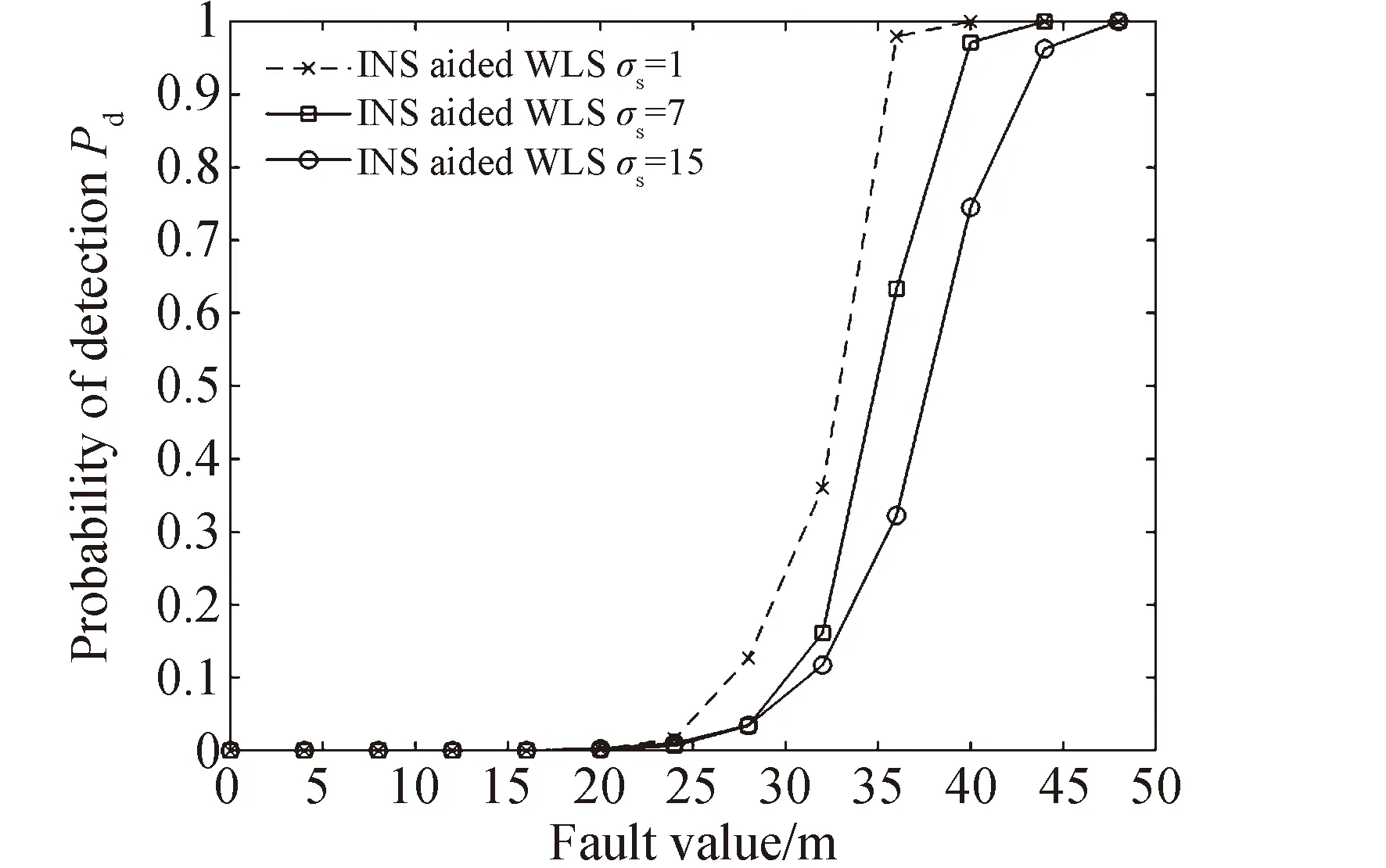
图9 不同INS定位误差方差的故障检测概率

2.2 仿真分析

从仿真结果中可以看出，对于35 m的阶跃故障，纯卫导加权最小二乘场景下并不能检测出所有历元中的故障，检测概率为48.51%。而在加入INS辅助之后，对于加入35 m的阶跃故障，对故障的检测概率达到97.21%。而且加入INS辅助之后对可见星的要求为不少于3颗即可进行完好性监测，相比加权RAIM算法要求的5颗可见星而言提高了算法可用性。

此外，从图3和图5对比可以看出，加入INS之后对位置误差也有所改善；从图6中可以看出，加入INS辅助后对GDOP值改善明显。GDOP最大值为1.45，比纯卫导加权最小二乘情况下的最小GDOP值1.63还要小，体现了加入INS辅助之后对于GDOP的改善。

图7中画出了最小二乘、加权最小二乘及INS辅助加权最小二乘3种算法的故障检测概率，仿真结果表明加权最小二乘算法对故障的检测性能优于最小二乘算法，而加入INS辅助之后的加权最小二乘算法对于相同的故障幅值，故障检测概率更高，均优于最小二乘法和加权最小二乘法。表4中展示了对于不同故障幅值3种算法对应的故障检测概率。

表4 3种算法的故障检测概率对比

图8展示了相同INS等级下本文所提故障检测方法与INS辅助的卡尔曼滤波残差χ2检测法的故障检测性能，对比可知本文所提算法对故障幅值具有更好检测性能，对40 m故障幅值检测概率为99.75%，而卡尔曼滤波残差χ2检测法的检测概率为34.4%。

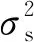
表5 不同INS等级的故障检测性能

3 结束语

为了提高RAIM算法的可用性和故障检测概率，提出了基于INS的多虚拟观测量的故障检测方法，通过理论分析与仿真验证表明：

1)加入INS辅助的加权最小二乘算法在故障检测和算法可用性方面都要优于传统的加权最小二乘RAIM算法。

2)加入INS虚拟星还可以改善GDOP值，提高定位精度。

3)加入INS虚拟卫星观测量后，当INS定位误差方差σs=1时加入35 m单星故障幅值，传统加权RAIM故障检测概率为48.51%，本文所提算法检测概率为97.21%，检测性能提升47%。在相同INS精度和故障幅值条件下，与卡尔曼滤波残差检测法相比，本文所提方法具有更高的检测概率，进一步验证了其在故障检测方面的优势。

4)不同INS精度对故障检测概率性能的影响：INS精度越高，即定位误差方差越小的情况下本文算法的故障检测性能提升越显著。