基于间接法在线能力评估和自主规划技术研究
2021-06-23湛康意陈海朋贺从园甘庆忠王禄
湛康意,陈海朋,贺从园,甘庆忠,王禄
上海航天控制技术研究所,上海 201109
随着航天技术的发展,高密集的发射任务已经成为常态。为了保证任务的成功,对运载火箭的可靠性提出了更高的要求。从目前国内外发射失利的情况来看,大约60%的故障源自于火箭动力系统。2009年,俄罗斯和欧洲联合研制的四级运载火箭联盟-2-1a,由于三子级提前关机,未能把卫星送入预定轨道。2011年,俄罗斯联盟-U在发射货运飞船任务中,三级发动机发生了燃料管路堵塞故障而导致任务失败。这些都是动力故障导致的[1]。对于一些非致命的动力故障,通过在线调整飞行程序,仍然可以保证任务的成功。美国土星1号运载火箭在一台发动机提前关机的情况下,通过调整关机时间进入预期目标轨道。美国猎鹰9号运载火箭在2012年的发射任务中,火箭一子级的一台发动机发生故障关机。通过在线规划新的上升轨迹,延长剩余发动机工作时间,将龙飞船送入预定的轨道,但是次要有效载荷OG2原型卫星被迫留置在较低的轨道[2]。国外火箭构型可以通过增加发动机来实现动力的冗余,能力较为充足,而国内现役运载火箭很难再增加一台发动机,在大多数卫星发射任务下,能力富余量较小。因此,在小能量故障情况下,当不能进入原目标轨道时,需要确定一个次优的救援轨道[3]。虽然现役的自适应迭代制导能够适应一定程度的推力偏差[4],但是推力下降后,为了维持弹道,攻角会变大,用于加速的推力分量减小,导致进入目标轨道时燃料不足,耗尽关机,不能成功入轨。这种情况下,就需要规划新的救援轨道。
国外在线规划技术已经有成功应用的例子,但是公开的文献却很少。国内目前还处于方案研究阶段,尚未在具体型号上应用。文献[5]提出了一种推力故障下的弹道重构策略,通过离线建立地面弹道库,设计救援轨道和相应的飞行诸元。一旦故障后,通过能力预测在线切换制导参数,实现故障情况下的弹道重构。为了覆盖可能的工况,该方法需要做大量的地面离线仿真工作。文献[6]提出了一种基于凸优化和自适应配点法的自主轨迹规划方法,设计了一套完整的自主规划流程。通过对地心角进行估计,采用凸优化求解一个具有相对精度的初值给自适应配点法,极大提高了自适应配点法的求解速度。该方法属于凸优化和自适应配点法相结合,求解过程复杂,对箭载计算机的性能提出了一定的要求。
针对运载火箭上升制导问题,基于间接法推导了许多制导方法,如迭代制导[7-9]、动力显示制导(PEG)等[10]。间接法的优势在于解的精度高且满足一阶最优性必要条件,对于一些动力学模型简单的问题,间接法具有一定的优势。国内外学者在间接法求解上升轨迹方面做了大量工作。文献[11-12]基于间接法研究了大气层内的上升制导,采用有限差分和密度同轮技术来求解两点边值问题。文献[13-15]也对该方法进行了研究,但是并没有考虑故障条件下的制导问题。文献[16]针对传统迭代制导小角度修正假设的不足,基于间接法研究了一种多终端约束的最优制导方法,并通过引入权重因子来提高制导方程数值求解精度。对于大气层外制导,不考虑过程约束,只需要求解满足终端目标的两点边值问题,即可确定最优轨迹。对于变目标轨道要素的制导问题,间接法不依赖标称轨迹,可用来实现轨迹的在线规划。
本文基于间接法,研究了一种大气层外的在线能力评估和自主规划方法,在发生推力故障的情况下,能够自主在线规划救援轨道。通过数值仿真,验证了方法的有效性、收敛性和实时性。该方法能够提高发射任务的可靠性,具有一定工程实用价值。
1 问题建模
1.1 动力学模型
假定发动机的推力始终沿运载火箭的体轴方向且为常值,则在发射惯性坐标系下建立运载火箭大气层外速度、位置无量纲化的运动模型:
式中:r∈R3为运载火箭相对发射惯性系的地心位置矢量;V∈R3为运载火箭相对发射惯性系的速度矢量;g0为标准海平面重力加速度大小;Tvac为发动机真空推力;Ib∈R3为体轴方向单位矢量;m是运载火箭的质量;μ为秒耗量。
1.2 最优问题描述
一般情况下,当发生动力故障,原目标轨道不可达时,重新规划轨迹后需要耗尽关机,充分挖掘火箭的潜力。在这种情况下,飞行时间基本确定,本文先构建末端时刻固定,以入轨点能量最大为最优性能指标的最优控制问题。
性能指标:
终端约束:
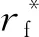
设哈密尔顿函数如下:
式中:λr∈R3、λV∈R3为协态变量;ν为乘子变量。采用极大值原理有:
求解可得:
协态变量方程为:
求解可得:
边值条件为:
式中:Ψ∈R3表示终端约束;ξ∈R3为乘子变量;λrf∈R3,λVf∈R3为协态变量终端值。消去乘子变量可得:
式中:Hf=rf×Vf为无量纲轨道动量矩。结合终端约束条件(2)~(4),可得到6个等式约束。至此,以入轨能量最大为最优性能指标的两点边值问题构建完毕。
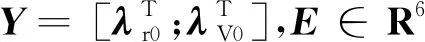
式中:0<β≤1;当‖Yk+1-Yk‖≤εY或‖E(Yk)‖≤εΨ,停止迭代,εY、εΨ为相应的收敛精度。
2 入轨能力评估
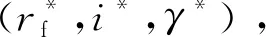
通过仿真发现,随着入轨高度hf的增大,入轨点速度先增大,后减小,存在一个使得入轨点速度最大的入轨高度,火箭飞行时间Tgo越长,相同入轨高度情况下,速度越大,见图1。当飞行时间较短,能力不足时,近地点曲线Hp与远地点曲线Ha没有交点,此时只能进入一个椭圆轨道,且存在一个使得近地点最高的入轨高度;当火箭飞行时间长,能力富足时,近地点曲线Hp与远地点曲线Ha存在两个交点,见图2。

图1 入轨点速度曲线
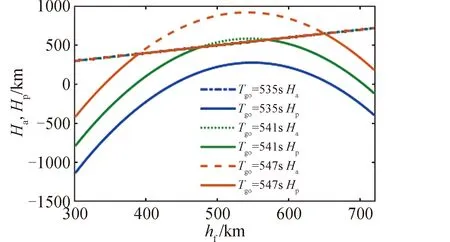
图2 远地点和近地点曲线
图3为近地点与远地点曲线存在交点的典型情况,hf1和hf2为远地点曲线与近地点曲线相交处的入轨高度。通过分析,可以得到以下结论:1)当入轨点高度小于hf1,或大于hf2时,在远地点入轨,且只能进入一个椭圆轨道;2)当入轨点高度为hf1和hf2时,可以进入一个圆轨道,其中,hf1对应最小的圆轨道,hf2对应最大的圆轨道;3)当入轨点高度在hf1和hf2之间时,入轨点为近地点,此时通过缩短飞行时间,也能够使得火箭进入一个圆轨道。同时,在hf1和hf2区间内,存在一个能量最大的轨道。
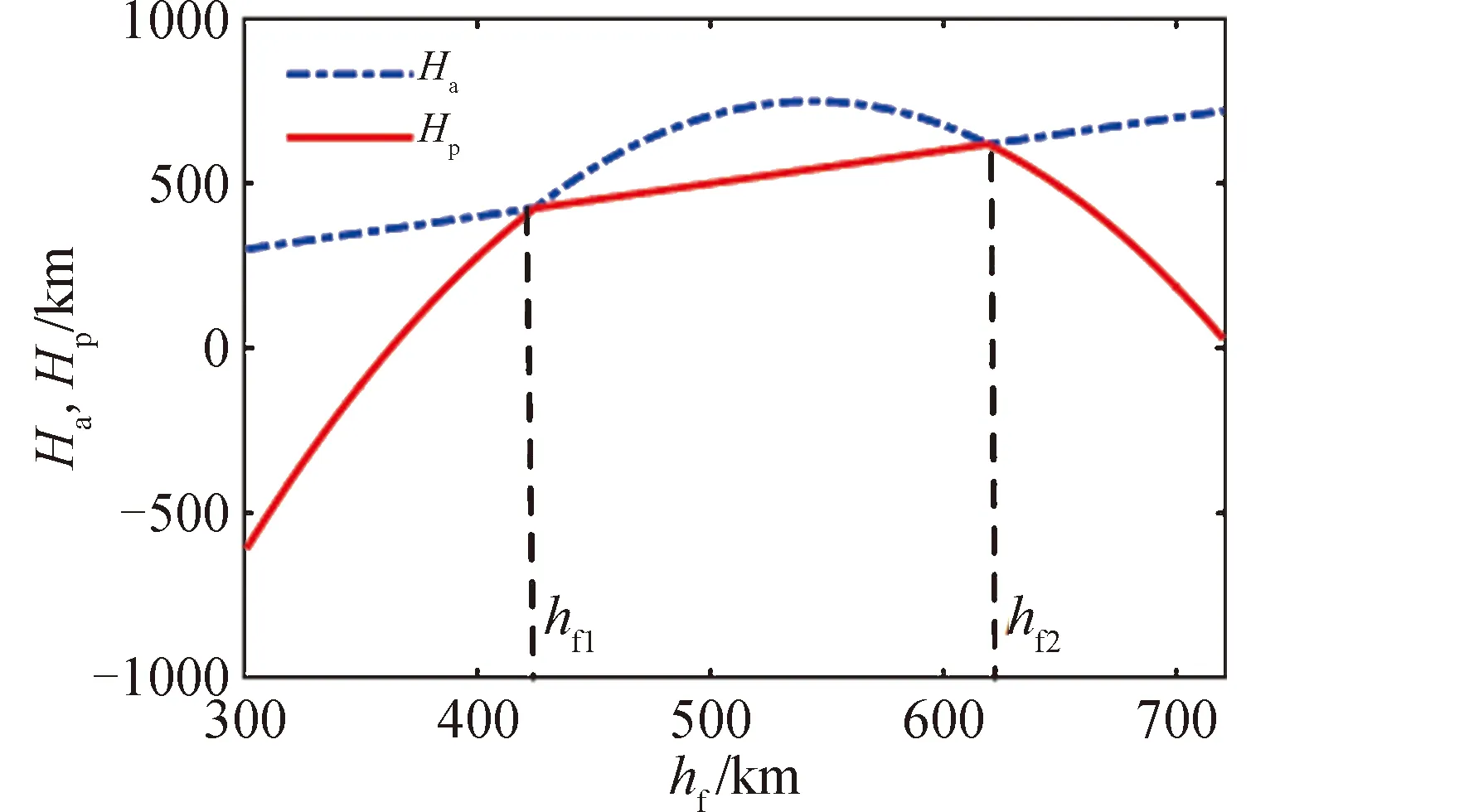
图3 远地点和近地点曲线(Tgo=544 s)
通过上述分析,可以设计如下的特征量Rk来判断运载火箭的入轨能力:
Rk=Ha(hf)+Hp(hf)-2hf
式中:Ha(hf)、Hp(hf)分别为轨道的远地点高度曲线和近地点高度曲线;hf为入轨点高度。则特征量Rk关于入轨点高度的曲线关系如图4所示。
图4中包含了不同飞行时间条件下特征量曲线与入轨高度之间的关系,通过分析可以得出如下结论:1)特征量曲线随着入轨高度的增大,先增大,后减小,存在唯一的极大值;2)当火箭飞行时间长,能力足时,特征量Rk的极大值大于零,有两个零点,大零点对应着最大的圆轨道,较小零点对应着最小圆轨道;3)当火箭飞行时间较短,能力不足时,特征量Rk的极大值小于零,此时火箭只能进入椭圆轨道。
3 自主在线规划策略
从算法层面上来看自主规划技术,需要解决故障的在线诊断和辨识[17],入轨能力在线评估,以及新的目标轨道在线规划等问题。在线故障诊断和辨识主要目的是提供当前火箭的推力、比冲、秒耗量、燃料质量等状态信息,为后面基于动力学模型的在线入轨能力评估和目标轨道规划提供输入信息,此内容不是本文重点工作,不在此赘述。入轨能力在线评估主要是基于当前的火箭状态信息,判断能否进入原目标轨道。当不能进入原目标轨道时,需要进行在线目标轨道重规划。
自主规划还需要确定新目标轨道的选取原则,针对救援问题,主要目的是让火箭能够进入一个安全的轨道,为后期的救援任务创造良好的条件。因此,本文在保证目标轨道倾角,放开升交点赤经约束的条件下,以近地点最高为救援轨道的选取准则。第2节的入轨能力分析,为在线目标轨道规划提供了基本依据。当能够入圆轨道时,近地点最高对应着最大圆轨道,需要求解最大圆轨道对应的入轨高度;当只能入椭圆轨道时,则需要搜索使得椭圆轨道近地点最高的入轨高度。
在此基础上设计了如图5所示的自主在线规划策略。
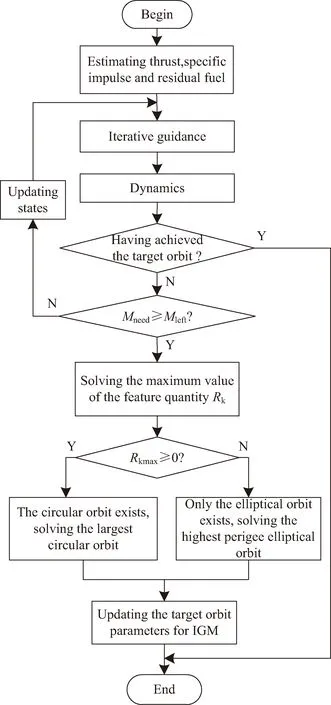
图5 自主在线规划策略
Step1:获取发动机推力、比冲和剩余燃料Mleft等信息。
Step2:按照原目标轨道参数,利用迭代制导求解程序角,数值积分运动学方程,计算消耗的燃料质量Mneed。
Step3:判断是否达到目标轨道。如果达到,则燃料充足,直接结束;否则,进入Step4。
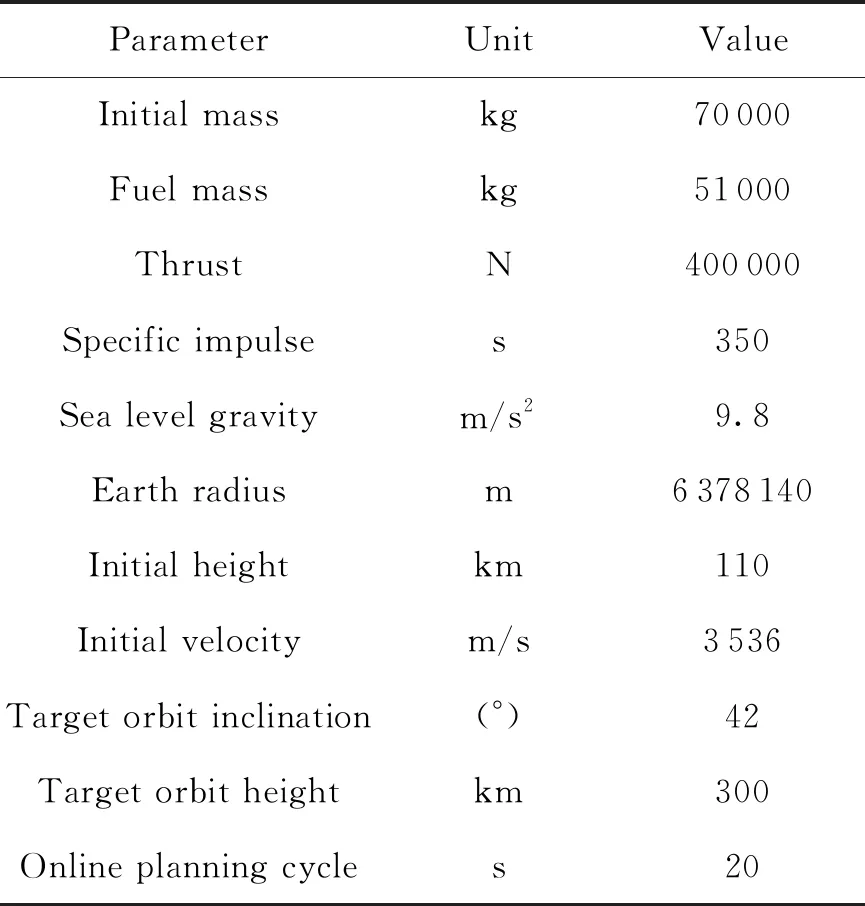
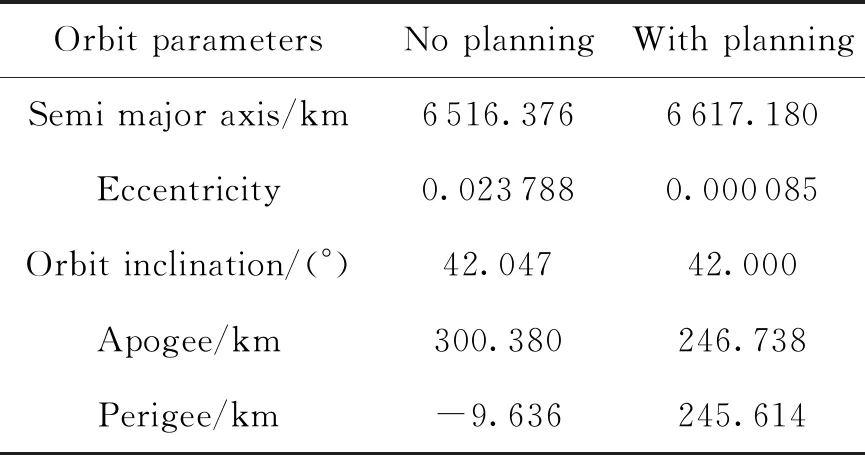
Step4:当Mneed≥Mleft时,燃料不足,需要重新规划目标轨道,进入Step5;当Mneed Step6:当特征量Rk的最大值Rkmax≥0时,存在圆轨道,进入Step7;当特征量Rk的最大值Rkmax<0时,只能入椭圆轨道,进入Step8。 Step7:以入轨高度为自变量,割线法[19]求解特征量Rk的最大零点,进一步求解对应的最大圆轨道,进入Step9。 Step8:以入轨高度为自变量,以近地点高度最大为优化性能指标。牛顿法求解近地点极大值对应的入轨高度,进一步求解相应的近地点最高的椭圆轨道。 Step9:更新迭代制导目标和参数,结束。 仿真参数如表1所示,设置故障时刻t=30 s,推力下降后占比75%,按目标半长轴或者燃料耗尽关机。 表1 仿真参数 图6为规划前后的仿真结果曲线,从图中可以看出,规划后降低了入轨高度,减少了侧向机动。从表2仿真结果可知,当在30 s发生推力下降故障时,如果不采用自主在线规划方法,燃料耗尽关机时,火箭只能进入一个300.380 km×(-9.636 km)的不可行轨道,任务失败;采用本文自主在线规划方案后,使火箭进入一个246.738 km×245.614 km的近似圆轨道,为后期的自主救援提供良好的条件。 表2 典型故障仿真结果 图6 典型故障仿真结果曲线 以故障时刻和推力下降后占比来刻画故障工况,并对故障工况进行网格化遍历仿真,采用燃料耗尽关机或半长轴关机。 图7(a)为传统迭代制导仿真结果,图7(b)为加入了自主在线规划策略后的仿真结果。图7中“*”表示300 km圆轨道,“o”表示近地点大于150 km安全轨道,“x”表示近地点小于150 km的不安全轨道。对比图7(a)(b)中的仿真结果可以看出,采用在线规划策略后,近地点小于150 km的工况显著减少,原来不能进入安全轨道的故障工况,采用在线规划后,可以进入一个近地点大于150 km的安全轨道,增大了火箭对故障的适应范围。其中,当推力下降到75%时,不采用自主规划,故障时刻只能适应70 s以后,采用自主在线规划,则故障时刻能够适应全程范围,保证任务安全。 图7 综合仿真结果 从仿真结果还可看出,原来不能进入300 km圆轨道的工况,在采用了在线规划后进入300 km的圆轨道,主要原因是第1.2小节中的间接法在约束处理上优先保证轨道倾角,放开了升交点赤经约束,使得轨道面在保证轨道倾角的前提下发生了挪动,减少了火箭垂直轨道面侧向机动的能力损失,充分挖掘了火箭的潜能。 本文在求解算法的设计上均基于成熟的数值方法。对于第1.2小节中的两点边值问题,由于有6个等式约束,6个协态变量初值,在有解前提下,问题解是唯一的。此外,协态变量主矢量λV跟实际的推力方向一致,而推力方向与速度方向之间的夹角通常不大,因此可以直接选择协态变量主矢量λV的初值为当前速度方向,协态变量λr初值为0,即可保证该两点边值问题迭代求解收敛。本文仿真环境为Intel Core i5-7500,3.4GHz,4GB RAM的电脑,编程环境为VS2013。仿真结果表明,自主规划算法在本文所有故障工况下均可靠收敛,完成一次自主规划平均耗时25 ms,满足实时性要求。 本文针对轨道救援问题,研究了一种基于间接法的在线能力评估和自主规划方法。仿真结果表明: 1)以入轨高度为自变量,基于最大能量轨道两点边值问题,数值分析得出的入轨速度、远地点和近地点跟入轨高度之间的关系具有普遍性。设计的自主在线规划策略,不仅可以适用于推力故障,后续还能用于火箭一子级提前关机故障。 2)构建的特征量,能够对入轨能力做出评估,判断当前状态下,火箭能够进入圆轨道还是椭圆轨道,为目标轨道选择提供依据。 3)自主在线规划策略具有明显的效果,部分不能进入安全轨道的故障工况,通过自主在线规划后进入了安全救援轨道,提高了火箭对故障的适应范围,增强了任务的可靠性。 4)自主在线规划算法子问题规模小,求解目标明确,求解算法简单,有解情况下能够可靠收敛。完成一次规划耗时短,满足制导实时性要求,针对轨道救援问题,具有一定工程实用价值。 5)目前的方法固定了轨道倾角,放开了升交点赤经约束,后续还需要综合考虑目标轨道倾角和升交点赤经的选择问题,进一步挖掘火箭故障情况下的潜能,使得火箭更加智能[20]。4 仿真结果及分析
4.1 典型工况仿真结果
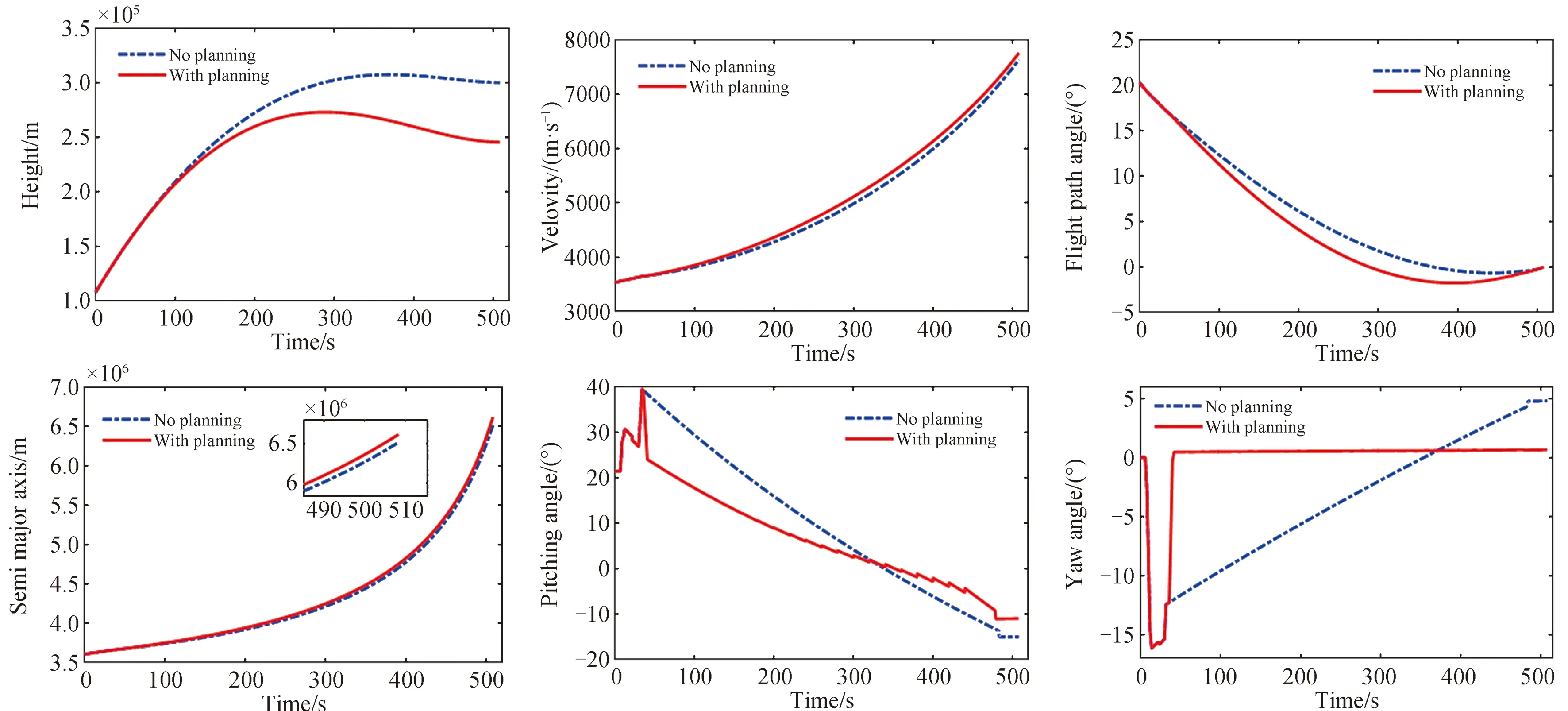
4.2 故障度与故障时间综合仿真
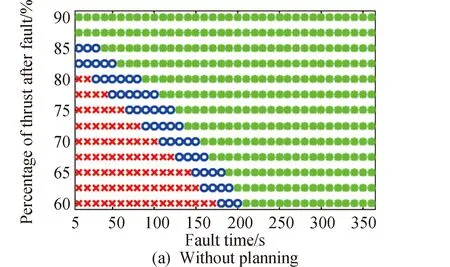
4.3 算法收敛性和实时性分析
5 结束语
