卫星光轴复合指向控制方法研究

鄢南兴，林喆,*，刘雅宁，于飞，王淳，康建兵

1. 北京空间机电研究所，北京 100094

2. 北京航天飞腾装备技术有限责任公司，北京 100094

随着卫星光轴控制技术的不断发展，其应用的范围也越来越广，涉及资源勘探、地理测绘、环境监测、天基测控等领域，尤其在天基测控领域，要求卫星光轴具备大范围指向、高精度和高机动性的能力。其典型应用为美国的“天基红外预警系统”，其搭载的光学载荷，能够迅速调整光轴，对天地运动目标实现跟踪指向[1-3]。

由于天基类卫星观测目标的特殊性，天基类卫星对空间目标的几何关系变化大，相对速度也大，最大的相对速度可达15 km/s。怎样在这样的高速条件下对目标进行观测和跟踪，是未来空间天基类卫星发展中需要解决的关键技术问题[4]。

目前，由于受到驱动器件性能、太空环境等因素限制，卫星姿态控制系统无法具备高机动性的能力，所以光电转台搭载光学成像系统的卫星载荷被引入以提升卫星光轴的指向性能是一种可行的方案[5]。最终的光轴指向由卫星姿态控制系统、光电转台控制系统、光学成像系统中的快反镜系统的输出叠加而成，以提升光轴的机动性、跟踪范围和跟踪精度。因此，如何设计卫星复合控制系统，将三分系统的输出有效叠加，达到光轴的稳定控制是一个难点。

解决此类复合控制的一种思路为主从设计法[6]，该类方法控制宏动系统跟随微动系统运动，实现指向运动中的大范围低频分量。文献[7] 提出了一种基于积分反演自适应滑模与改进主从控制结合方案。文献[8]引用一种自适应模糊PID的算法提升跟踪精度。文献[9] 利用施奈尔反射镜定律的矢量方程,构建系统视轴矢量方程,研究其运动特性、稳定补偿原理，提高了控制系统的带宽。

除了主从设计法，文献[10-11] X. H.Huang 和R. Horowitz等人从宏动、微动系统之间的耦合关系出发，将宏-微系统整体作为被控对象通过H2/H∞方法给出了复合控制器的设计方法。文献[12] 提出了将内、外环架系统视为整体的多变量控制结构，通过μ 综合法设计多变量控制器使系统的稳定精度和快速性有所提升。但是这类设计结果的控制器往往阶数较高，工程上实现比较复杂。

本文针对卫星光轴复合指向控制系统，提出了一种复合控制方法，使得卫星姿态控制系统、星载转台系统和快反镜系统协同工作达到稳定控制卫星光轴的目的，从而提升了卫星光轴的指向范围、机动性、伺服精度。

1 系统模型分析

天基类卫星围绕地球轨道运动，对运动目标进行跟踪成像，通过对目标的捕获和图像处理，算出卫星光轴与目标的夹角，通过控制卫星光轴做出相应的角度调整，从而保持对目标的跟踪指向。

天基类卫星搭载光电转台的光轴指向系统模型如图1所示，在卫星平台上安装了二维旋转机架，机架上搭载光学载荷，在光学载荷的光信息通路中安装了快反镜。卫星姿态系统接收复合指向控制器的信号r3实现低频大角度的转动，但是由于其性能的限制，姿态转动速度慢，对快速运动的目标会有很大的静差，但通过卫星姿态的转动，可以提升卫星光轴的指向范围；光电转台完成二级的角度补偿，完成对卫星姿态系统的偏差的补偿，使得卫星光轴具有更高的机动性应对视场内各种目标的相对运动；最后通过快反镜响应高频小角度的信号完成角度的二级补偿，同时隔离卫星平台各类的高频扰动信号。

图1 星载光轴指向系统组成框图

姿态控制系统一般由卫星本体、星载计算机、星敏感器和执行机构组成，其控制系统组成如图2所示。可知，卫星的姿态信息由星敏感器、太阳敏感器、传感器反馈到输入端作差，通过控制器给出最终的期望力矩命令[13]。

图2 卫星姿态控制系统组成框图

光电转台由三相永磁同步力矩电机驱动旋转机架，在旋转机架上安装了光学载荷，光电码盘作为位置反馈器件，采用速度，位置双闭环控制方式以克服转台的轴系摩擦和线缆拖拽等外部扰动[14]。光电转台控制系统组成如图3所示。

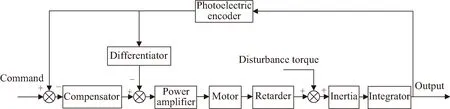
图3 光电转台控制系统组成框图

快速反射镜是一种精密的跟踪技术[15]，它主要用于校正卫星平台的跟踪误差，提升视轴稳定的指向精度，采用了音圈电机驱动的快速反射镜的闭环控制系统框图如图4所示。

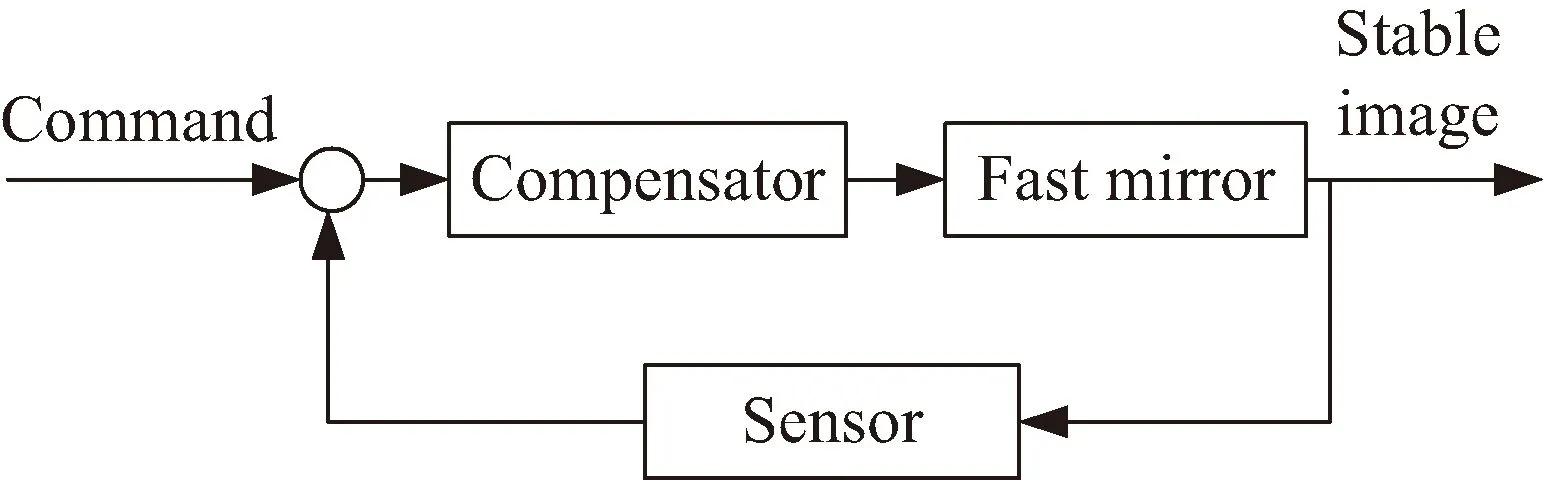
图4 快速反射镜控制系统组成框图

卫星光轴复合指向控制系统由上述三个子系统组成，由复合指向控制器进行控制，其系统的控制结构原理图如图5所示，其中，复合指向控制器接收调整指令，并将其转化为姿态控制系统的指令r3、转台控制系统指令r2和快反镜系统指令r1。姿态控制系统接收复合指向控制器的输出的指令r3后，与星敏感器反馈的当前姿态角作差给到姿态控制器，姿态控制器输出驱动飞轮，带动卫星完成姿态调整。光电转台接收信号r2后，与光电码盘反馈的实时角度作差，经过位置控制器后得到光电转台的速度控制量，速度控制量与光电转台反馈的速度信号(码盘位置信号做微分)作差算出电机驱动量Vm，驱>动机架电机产生控制力矩Tm，驱动旋转机架跟踪给定信号完成光电转台的惯性稳定与指向跟踪功能。快反镜接收驱动指令r1，快速反射镜在r1驱动下改变快反镜角度使反射光束发生偏转，从而实现小角度的光束指向调整。

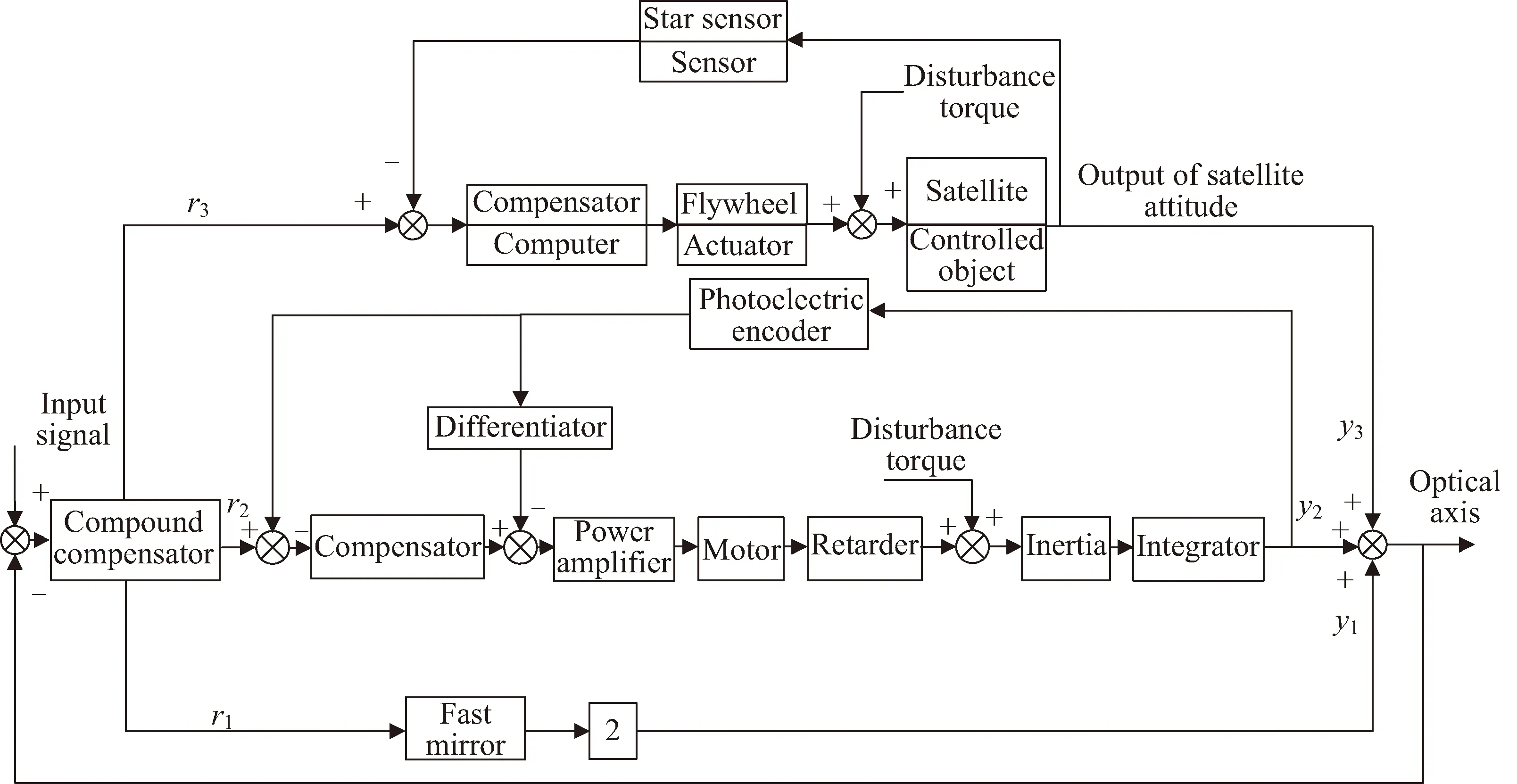
图5 卫星光轴复合指向系统组成框图

考虑到姿态控制系统从接收输入指令r3到输出的传递函数可用G3(s)表示，则输出的姿态角可表示为:

y3=G3(s)×r3

(1)

光电转台控制系统中的控制器、功放、减速器、惯量分别可用比例系数Kc、KP、KI、1/JDS表示，机架电机的传递函数为H(s)=Kt/(Ls+R)，码盘特性表示为M(s)，速度回路的闭环传递函数J2(s)=KPKIH(s)/[JDS+KPKIH(s)M(s)S]，光电转台的位置环闭环传递函数为:G2(s)=M(s)J2(s)Kc/[(1+J2(s)KcM(s))]，光电转台产生的驱动量到y2的传递函数可表示为：

y2=G2(s)×r2

(2)

快反镜的从输入指令到产生的偏转角度间的传递函数可用J1(s)表示，则从快反镜驱动信号r1到所产生的光路偏转的传递函数可表示为G1(s)=J1(s)×2，则快反镜控制系统的输入输出关系可以表示为：

y1=G1(s)×r1

(3)

系统的控制结构可以简化为图6所示。

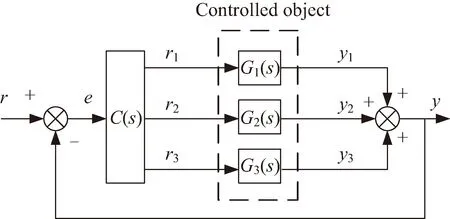
图6 简化后卫星光轴复合指向系统框图

至此，卫星光轴复合指向系统的控制问题转化为如何设计复合指向控制器C(s)能够协调控制三个并行的被控子系统，使得姿态控制系统完成初步的卫星姿态调整，光电转台完成进一步大范围的光轴转动，快反镜系统响应高频小角度信号，最终三个子系统的输出量有效叠加从而得到精确的卫星光轴指向。

2 卫星光轴复合指向控制器设计

考虑到卫星光轴复合指向控制系统的3个子系统的系统带宽不同，设计复合指向控制器C(s)由5个控制器组成[16]，其中C31，C32决定了光电转台系统和快反镜系统的响应频带，C21，C22决定了光电转台系统和卫星姿态控制系统的响应频带，C11控制器用于调整卫星光轴复合指向系统的整体性能和稳定性，所以卫星光轴复合指向系统的控制结构进一步转化为图7所示。

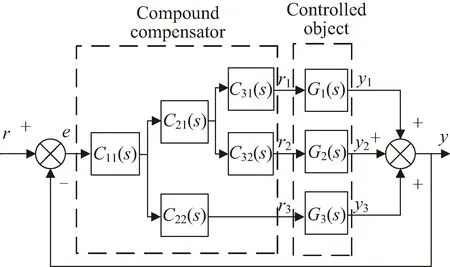
图7 转化后卫星光轴复合指向系统框图

首先设计控制器C31和C32，先建立一个辅助单位反馈闭环系统,如图8所示。

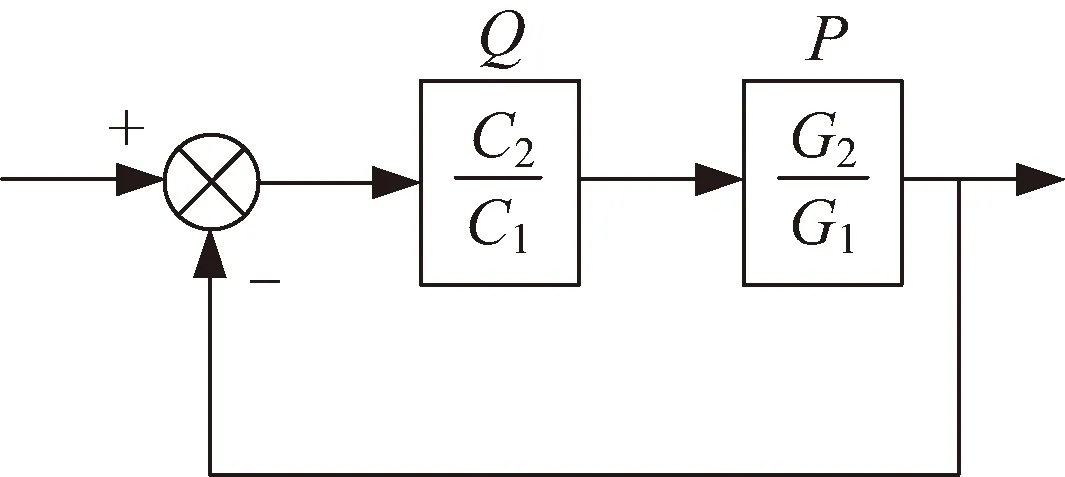
图8 辅助单位反馈系统框图

取比值传递函数:

P=G2(s)/G1(s)

(4)

设计虚拟控制器:

Q=C32(s)/C31(s)

(5)

辅助单位反馈系统以光电转台系统和快反镜系统的传递函数的比值作为设计对象，如果PQ>1，即|C32(s)×G2(S)|>|C31(s)×G1(S)|，则表明光电转台系统占据主导响应，反之，当PQ<1, 则表明快反镜系统占据主导响应。当PQ=1，表明光电转台系统和快反镜系统响应幅值相等。∠PQ(ω)表现为两个系统输出的相位差，当∠PQ(ω)=-180°时，两支路相位相反，输出互相抵消，所以为了让两系统的输出有效叠加，需要设计控制器Q保证辅助单位反馈系统的相角裕度大于60°，同时其穿越频率点作为两系统输出的频带分界点。

根据频率响应法设计控制器Q,以两系统的特性选取穿越频率ωc1，相角裕度大于60°的准则进行设计得到Q。为了C32(s)的阶数不至于太高，取C31(s)为常数，即C31(s)=K根据公式(5)，得 ：

C32(s)=Q(s)×K

(6)

将公式(6)带入图8，光电转台系统和快反镜系统的综合传递函数可表示为：

G4(s)=G1(s)×C31(s)+G2(s)×C32(s)

(7)

图8转化为如图9所示：

图9 第一次转化后卫星光轴复合指向系统框图

以G4(s)和G3(s)为被控对象，用上述方法设计控制器C21和C22，确定G4(s)和G3(s)的频带分解点ωc2，得到姿态控制系统、光电转台系统和快反镜系统的综合传递函数可表示为：

G5(s)=[G1(s)×C31(s)+G2(s)×C32(s)]×

C21(s)+G3(s)×C22(s)

(8)

则图9可转化为图10所示：

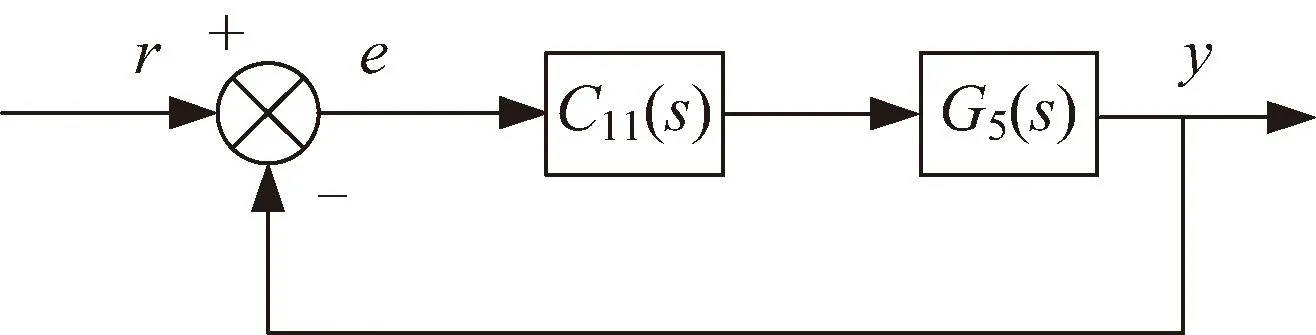
图10 第二次转化后卫星光轴复合指向系统框图

以G5(s)为最终的被控对象，根据对卫星光轴复合指向系统的性能要求，运用频率响应法设计控制器C11(s)。

根据上述设计，卫星光轴最终的指向位置为

y=y1+y2+y3=C11×C21(s)×C31(s)×G1(s)×

e+C11×C21(s)×C32(s)×G2(s)×e+C11×

C22(s)×G3(s)×e

卫星姿态控制系统主导响应频率低于ωc2的信号，光电转台控制系统主导响应频率介于ωc2和ωc1之间的信号，快速反射镜控制系统主导响应频率高于ωc1信号，有效解决了各个子系统的频带分解问题，使得输出可以有效的叠加。

3 仿真试验

卫星在某轨道F对某轨道G物体进行光轴指向跟踪，经过简化其相对运动轨迹如图11所示，运动目标相对于卫星光轴以做等高8 km的匀速直线运动，由A飞到C点，相对速度为1.2 km/s，卫星和目标初始距离为64 km，要求光轴指向的范围达到0～165°，对目标的指向跟踪误差保持在±0.05°范围以内，跟踪带宽应高于18 rad/s。以卫星单自由度水平方向运动作为仿真环境，光电转台的驱动范围可以达到±90°，卫星姿态能够进行360°的调整，光轴初始指向即为目标。光轴初始指向方向垂直于卫星平台为卫星初始姿态。

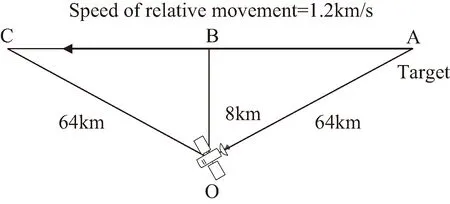
图11 卫星光轴相对运动轨迹

对简化后的卫星光轴相对运动轨迹信号做傅里叶变换，得到其频谱如图12所示，可知其信号频谱主要集中在低于1 Hz处。

图12 输入信号频谱

该卫星的快速反射镜控制系统的以音圈电机作为驱动器，其作动范围为±2°，通过系统辨识，其输入信号到快反镜偏摆的角度的传递函数表达式如下：

光电转台其输入信号到机架转动的角度的传递函数的表达式如下：

卫星姿态控制系统其输入信号到卫星的转动的角度的传递函数表达式如下：

经上述计算后，根据公式(7)得到：

首先设计控制器C31和C32，根据公式(4)得到P的传递函数表达式为：

因为G2(s)是典型的二阶带阻尼震荡环节，可得到光电转台的系统的闭环带宽为20 rad/s，所以选取ωc1=18 rad/s作为快反镜系统和光电转台系统的频带分界点，以60°的相角裕度为设计指标，对P用频率响应法[17-19]进行设计得到：

根据公式(5)(6)，故常数项的控制传递函数取1，得到：

以G4(s)和G3(s)为被控对象，设计控制器C21和C22，卫星姿态控制系统的闭环带宽为0.1 Hz，根据输入信号的频谱图，0.1 Hz以上频率的信号能量比重不小，为了让卫星光轴具有更好的机动性能，则姿态控制系统和光电转台的频带分界点要略低于姿态控制系统的闭环带宽，所以选取ωc2=0.1rad/s作为姿态控制系统和光电转台的频带分界点，常数项控制器的传递函数取1，得到：

C21=1

根据公式(8)可得：

G5(s)=

以G5(s)为最终的被控对象的卫星光轴复合指向系统，按照上述的卫星光轴复合指向控制系统的系统性能要求，运用频率响应法设置控制器C11(s)，得到：

至此，卫星光轴复合指向控制系统的开环传递函数为C11×G5其波特图如图13所示。

可以看到，卫星光轴复合指向控制系统的带宽为24.3 rad/s，相角裕度61°，从图13的开环波特图可以看出，在低频段卫星姿态控制系统具有高增益，中频段具有相应的稳点裕度，高频段迅速衰减，满足了经典控制理论中的对动态特性和稳定性的要求。

图13 卫星光轴复合指向控制系统开环传递函数波特图

如图14所示，低于0.1 rad/s的频段，卫星姿态控制系统的幅值响应大大高于其他两个子系统，占据主导响应，当频率高于0.1 rad/s后，卫星姿态控制系统的幅值响应曲线迅速衰减；同理，在0.1 rad/s和18 rad/s的频段，光电转台系统的幅值响应高于其他两子系统，占据主导响应，高于18 rad/s后，幅值迅速衰减；在高于18 rad/s的频段，快反镜系统占据主导响应。综上所述，本设计完成了卫星光轴复合指向控制系统的频带分解问题，卫星姿态控制系统主导响应低频大角度信号，光电转台系统主导响应中频段信号，快反镜系统响应高频小角度信号。

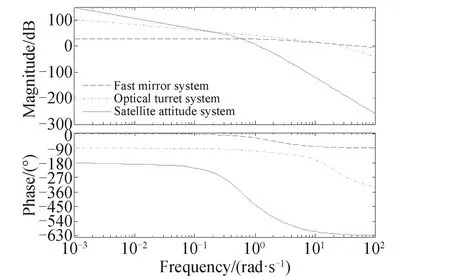
图14 卫星姿态控制、光电转台、快反镜系统开环波特图

根据卫星光轴跟踪目标的输入信号曲线，观察卫星光轴复合指向系统的各子系统的响应曲线如图15所示，输入信号的初始角度变化速度较慢，姿态控制系统能够主导响应其信号，但由于姿态控制系统的带宽低，机动性弱，渐渐无法跟上输入信号。此时，光电转台开始补偿卫星姿态跟目标光轴的角度静差，使得光轴能够保持对目标的持续的跟踪指向。当跟踪信号角度逐渐放缓，姿态控制系统出现超调，光电转台和快反镜迅速响应，将超调反向迅速补偿，使得光轴始终稳定跟踪指向目标。快反镜始终响应高频的小角度信号，对整个光轴跟踪指向过程起高频补偿作用。

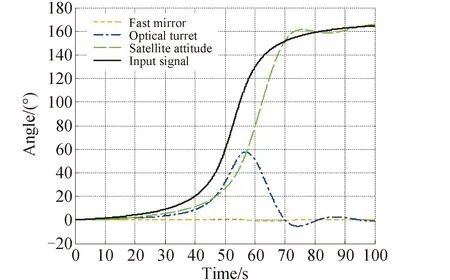
图15 系统响应曲线

由图16可知，当只依靠卫星姿态控制系统对目标执行光轴跟踪指向仿真试验时，由于姿态控制系统的低带宽特性，无法跟上目标，导致其跟踪误差达到了30°。当只用光电转台对光轴进行跟踪指向时，其跟踪误差降到了0.6°，当运用卫星光轴复合指向控制系统驱动卫星光轴跟踪指向误差降低到了0.05°以内。通过对以上3种情况的仿真结果对比，证明了卫星光轴复合指向控制律设计的有效性，其协调调动了卫星姿态控制系统，光电转台系统，快反镜系统协同运动，有效叠加了三者的输出，使得卫星光轴的指向范围更大，跟踪指向精度更高。

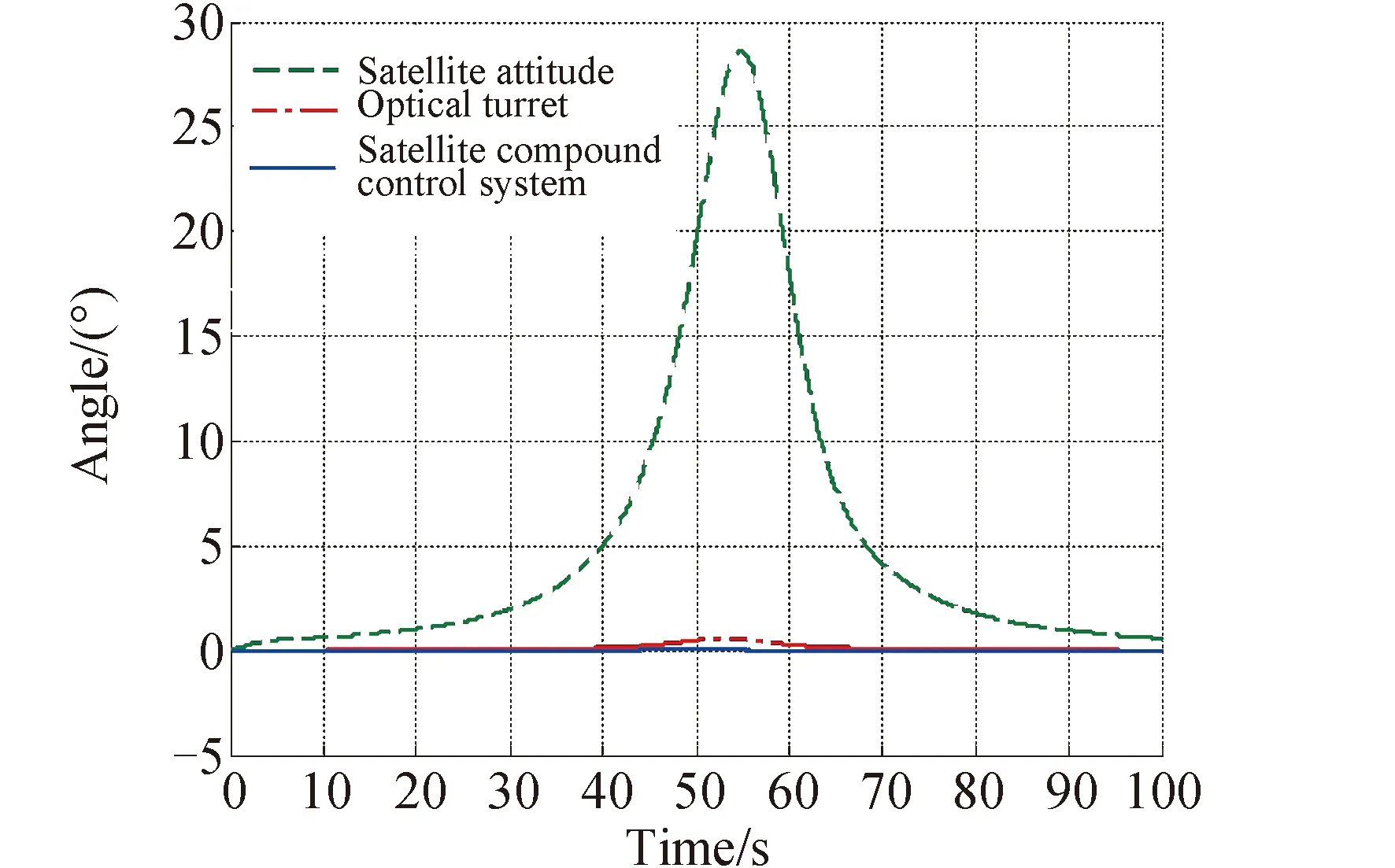
图16 误差曲线

4 结束语

卫星光轴对空间高速运动目标进行跟踪指向是天基类卫星的重要功能之一，单纯的依靠卫星的姿态调整能力限制了光轴的跟踪指向性能，为此，通过对卫星姿态、光电转台、快反镜系统的协同控制运动，从而大幅提升卫星光轴的指向范围、机动性和精度是可行的方案。基于此，本文针对此卫星光轴指向复合控制系统，研究了卫星姿态控制系统，光电转台系统，快反镜系统的特性，提出了一种卫星光轴的复合指向控制方法，有效地解决了卫星光轴各子系统协调工作和复合控制系统的子系统的工作频带分解问题，实现了对卫星姿态，光电转台，快反镜的三重复合控制，并且有效地提高了卫星光轴的跟踪指向范围、机动性、伺服精度。相较与其他复合控制的设计方法，其具有设计过程较为简单，计算量偏小的优点。该方法为未来空间天基类卫星的光轴指向类控制系统的设计提供了一种新的思路。