长江经济带省域绿色全要素生产率测算与收敛性分析
2021-06-22于善波张军涛
于善波 张军涛
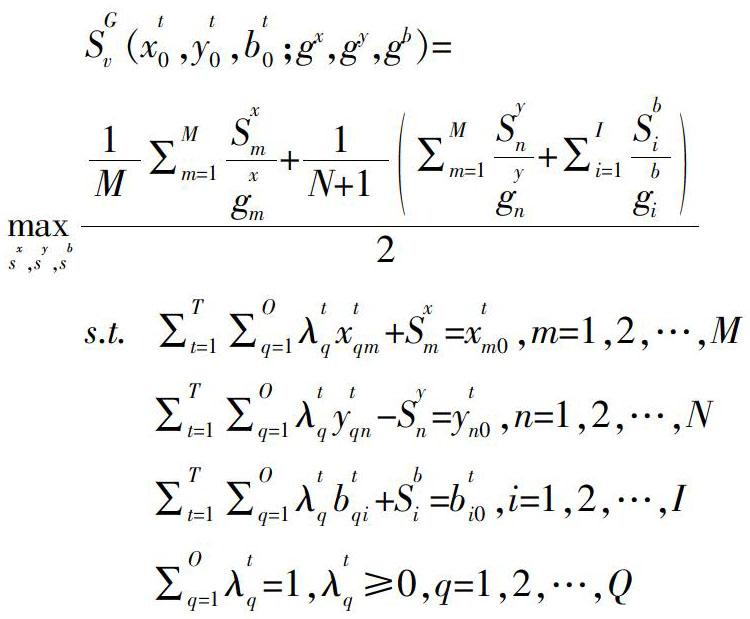

摘 要:基于SBM-GML模型,以2005—2019年长江经济带省级面板数据为样本,测算长江经济带省域绿色全要素生产率,并对其收敛性进行了分析。研究结果表明:长江经济带省域绿色全要素生产率在样本期内有效,虽然表现出短期波动,但是整体而言,波动幅度不大,并且在2010年之后呈逐年递增态势。其中,技术效率是提高省域绿色全要素生产率的主要原因,规模效率不高影响了省域绿色全要素生产率的水平。同时,长江经济带省域绿色全要素生产率不存在显著的α收敛,但是存在绝对β收敛。即省域绿色全要素生产率在时间序列上并不具有延续性,省域绿色全要素生产率低的省份存在向绿色全要素生产率高的省份的“追赶效应”,并将最终以相同的稳态趋于均衡。为此,要坚定不移贯彻新发展理念,倡导绿色转型发展;提高规模效率,突出城市聚集效應,充分发挥城市群在带动区域经济增长和转型中的作用;在具体政策制定上,要注重省域发展的差异性,做到精准施策。
关键词:绿色全要素生产率;SBM-GML模型;收敛性;长江经济带发展
中图分类号:F127 文献标识码:A 文章编号:1003-7543(2021)04-0068-10
以高投资、高能耗和高排放为特征的发展模式不利于我国经济社会的可持续发展。长江经济带在经济快速发展的同时,面临着资源环境的约束,特别是工业化和城镇化进程的加速推进,带来了空气污染、水污染、垃圾围城等问题。2019年,长江经济带城镇化率达到60.60%,按照国际经验来看,已经进入社会矛盾的多发期,同时环境承载压力逐渐加大。在“共抓大保护、不搞大开发”成为长江经济带沿线省市发展共识的背景下,推动长江经济带高质量发展、实现绿色转型已经成为破解环境污染难题、提升可持续发展能力的重要抓手[1]。那么,长江经济带沿线省市绿色发展效率如何?各省市之间绿色发展效率的差异又有多大?这些问题亟待回答,对于客观评估长江经济带省域发展潜力具有重要的理论价值和现实价值。
一、相关文献综述
经济增长与资源环境之间的关系,一直以来都是学术界探讨的热点。如何在资源环境承载能力范围内,实现又好又快的发展,是我们面临的现实性问题。长期以来,我国经济的高速增长是以较大的资源耗费和环境污染为代价的。为了更好地发展经济,就需要提高绿色全要素生产率。这是实现经济高质量发展的关键。绿色增长模式强调的是低资源消耗、低污染排放,以及经济增长与资源消耗、污染排放的脱钩[2]。这种发展模式是对以往经济发展思路的改变,也是未来经济社会发展的趋势。
就长江经济带而言,长江经济带在近20年来的发展历程中,虽然显著提高了经济社会发展水平,城市发展规模亦有所提升,但也面临着绿色增长动力不足的困境[3]。学术界对长江经济带实现资源环境约束下的高质量发展问题进行了深入探讨,现有文献中,学者们普遍认为,实现长江经济带绿色发展,就需要转变现有发展思路,促进绿色与发展协调推进,实现经济和环境良性互动。
现有关于省域绿色全要素生产率的文献中,江艳婷等认为,技术效率改善是提高我国省域绿色全要素生产率的重要原因,而技术进步则成为其滞后因素[4];陈黎明等测算得出,地理邻接是区域绿色全要素生产率空间溢出的主要途径,其增长主要依靠技术进步[5];任阳军等指出,虽然区域全要素生产率存在空间溢出效应,但是技术效率的改善是区域绿色全要素生产率提升的主要原因,技术变化则起负向作用[6]。具体到长江经济带绿色全要素生产率的研究中,多数文献都是将研究焦点放在地级市层面。韩晶等指出,长江经济带沿线城市绿色发展水平在时序上呈现“M”型的上升路径,绿色发展水平逐年提高[7];李汝资等认为,长江经济带城市绿色全要素生产率变化在局部热点区域表现为上游、中游、下游“哑铃”型分布,且由下游地区逐步转移至上游地区[8]。也有文献将研究的样本界定在省级层面,但是测算的是农业绿色全要素生产率[9]和工业绿色全要素生产率[10]。在具体模型选择上,涉及SYS-GMM估计方法[2]、方向性距离函数(DDF)[3]、ESDA方法[11]等。
综上所述,现有关于长江经济带省域绿色全要素生产率的测算并不多见,且较少将非期望产出作为分析要素纳入模型,造成了计算省域绿色全要素生产率时容易出现偏差。因此,需要对长江经济带省域绿色全要素生产率进行更为深入的分析,以客观反映长江经济带沿线省市绿色发展过程中存在的问题。基于此,本文的边际贡献在于基于SBM-GML指数模型,测算了长江经济带省域绿色全要素生产率,并分析了其是否存在α收敛和绝对β收敛,进一步探讨了省域发展的内在机制,明确了各省域发展间的差距。
二、模型设定、指标选取与数据说明
(一)模型设定
在计算全要素生产率的过程中,已有学者开始关注将资源、环境等要素考虑在内[12];即通过加入反映能源消耗和污染物排放的变量来衡量绿色发展[13]。这种思路由Pittman等首次将污染作为非期望产出置于生产函数中[14],随后,Chung等也将污染排放列入非期望产出用以研究其对经济增长的作用[15],而我国较早提出绿色全要素生产率的学者是李俊等,他们在研究中加入了反映环境变化的变量[16]。目前针对全要素生产率的测算主要包括索罗余值法、DEA方法和SFA方法。索罗余值法和DEA方法在模型运算时的思路是,将污染排放以生产投入的形式参与计算,它无法模拟污染排放的产出形态。这催生了方向性距离函数(DDF)的出现,其可以解决非期望产出与期望产出的方向性问题,但仍需要基于径向性和角度性的假设要求[17],同时,其对无效DMU的测量仅包含投入、产出变量的比例变动,而忽略了非零松弛项的改进[18]。为克服这一局限,Fukuyama等将DDF与SBM综合后提出方向性SBM的概念,并得到了全局方向性SBM模型[19]。
(二)指标选取与数据说明
根据模型选择以及研究问题需要,本文在参考江艳婷等[4]、陈黎明等[5]、任阳军等[6]的研究的基础上,选取劳动力、资源、资本三个要素作为投入指标。其中,用全部从业人员数作为劳动力投入要素,用土地资源(建成区面积)、水资源(供水总量)作为资源投入要素,用固定资产投资总额作为资本投入要素;而用地区生产总值(GDP)、地方政府财政收入和社会消费品零售总额三个指标刻画期望产出;选用工业二氧化硫排放量、工业烟尘排放量、工业废水排放量三个指标反映非期望产出。
在时间跨度的选择上,早在20世纪90年代长江经济带就已经被纳入国家战略,其中最具有代表意义的是1990年国务院批准的《长江流域综合利用规划简要报告》。2005年,江苏省、安徽省、江西省、湖北省、湖南省、四川省、云南省、上海市和重庆市共同簽订了《长江经济带合作协议》,这也为后续长江经济带发展奠定了较好的基础。为考察较长时期内长江经济带省域绿色全要素生产率,同时考虑到数据的可获取性等原则,本文选取的数据为2005—2019年长江经济带沿线11省市的面板数据,数据主要来源于《中国统计年鉴》《中国环境统计年鉴》等。针对部分缺失数值,本文根据《中国城市统计年鉴》、《中国统计年鉴》、各省市国民经济和社会发展统计公报,采取均值插补方式得到。
三、长江经济带省域绿色全要素生产率的空间差异分析
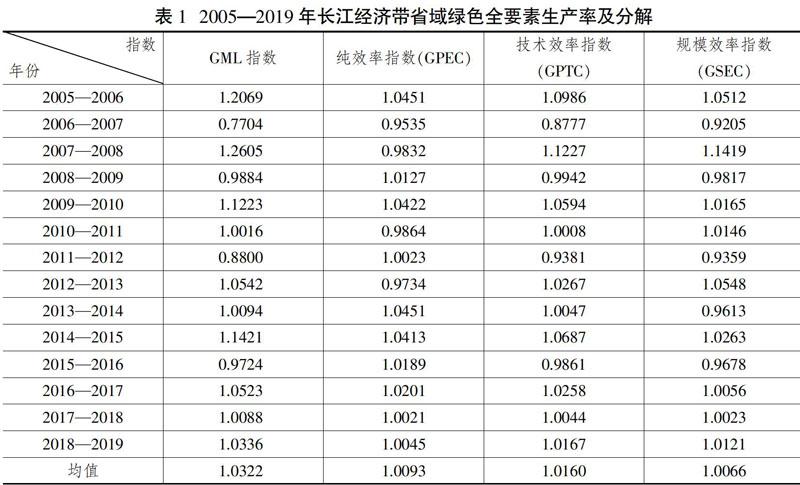
由GML指数公式,可以计算得到长江经济带省域绿色全要素生产率(见表1,下页)。由表1可知,2005年以来,长江经济带省域绿色全要素生产率的均值为1.0322,整体而言,均为有效。但是,也表现出了波动性,其中在2009年之前,长江经济带省域绿色全要素生产率呈现“V”型分布,低点出现在2009年,仅为0.9884。而在2010年之后,长江经济带省域绿色全要素生产率呈现缓慢递增态势,虽有短期波动,但是浮动不大。这主要是因为,2008年全球性金融危机波及了我国经济发展,受金融危机影响,长江经济带经济发展速度趋缓,产出效率不高。而伴随着经济逐渐恢复,以及政府对经济社会发展的认知不断深化,绿色发展效率逐年增强。特别是在2013年之后,长江经济带省域绿色全要素生产率递增态势明显。这主要是由于长江经济带作为区域发展战略被正式提出,各省市发展思路已经发生变化,这也成为长江经济带省域绿色全要素生产率逐年递增的原因。从影响全要素生产率的因素来看,技术效率是影响省域绿色全要素生产率的主要原因。
表2(下页)显示了沿线各省市绿色全要素生产率及分解情况。2005年以来,长江经济带沿线省市GML指数均大于1。从区域来看,下游地区的上海市最高,为1.2034,而上游地区的贵州省最低,为1.0036。具体而言,11个省市又表现出了较为突出的三极分布,即长江经济带下游、中游、上游地区呈现一定的差异。从三大地区的省域绿色全要素生产率分解因素来看,也表现出了较强的地区差异性。三大地区中,长江经济带下游地区的省域绿色全要素生产率要总体高于中游和上游地区。
就地区差异而言,图1(下页)反映了长江经济带上游、中游和下游地区的省域绿色全要素生产率情况。数据显示,下游地区省域绿色全要素生产率要高于上游和中游地区,各省市绿色全要素生产率均有效,即三个地区的省域绿色全要素生产率均大于1,其中,下游地区省域绿色全要素生产率为1.1208,上游地区为1.0211,而中游地区为1.0383。具体分因素来看,技术效率是推动省域绿色全要素生产率变化的主要原因,这表现出了和全国同步的趋势,也表明在样本期内,三个地区的技术效率水平不高,应该在未来发展过程中更加关注投入产出效率,更加关注可持续发展与资源环境约束之间的关系,在有限的资源要素投入下,实现各投入要素的产出最大化。
四、长江经济带省域绿色全要生产率的收敛性分析
新古典增长模型认为经济发展的最终状态是趋于稳定的,即必然存在收敛。长江经济带实现绿色转型发展,就需要对其内部发展差距作出更为细致的分析。前文已经证实,长江经济带省域绿色全要素生产率存在地区差异,但是,这种地区间的差异是否会伴随着时间的变化而产生变动值得进一步探讨。为了更加清晰阐明长江经济带省域绿色全要素生产率的省际差异,以及未来是否会趋于平衡发展,有必要计算其收敛性。
现有文献认为,计算收敛性主要集中在α收敛、绝对β收敛和条件β收敛三种形式上[21—22],三种计算方法因其侧重点不同而产生不同结果。
(一)α收敛性分析
α收敛能够阐明长江经济带省域绿色全要素生产率在时间趋势上的变化情况,也能够反映其离散程度。如果伴随着时间的变化,该指标数值降低,则表明长江经济带省域绿色全要素生产率存在收敛性,否则为发散。本文在赵磊[23]研究的基础上,利用标准差来计算长江经济带省域绿色全要生产率是否存在收敛性。同时,为了研究的严谨性,本文也计算了变异系数。图2(下页)显示,长江经济带省域绿色全要素生产率并没有出现随时间变化而下降的趋势。反而,α收敛随着时间的变化而逐渐递增,大致呈现“W”型分布,在2006年和2009年达到了最低值,分别为0.2189和0.1789。其余年份,尤其是2010年之后,呈现逐年递增趋势。由此可见,长江经济带省域绿色全要素生产率并不存在显著的α收敛。为更好地验证该结论,从变异系数的角度来看,也未出现随时间变化而缩小的趋势。
从长江经济带上中下游地区的横向对比来看,图3(下页)显示,三大地区省域绿色全要素生产率并不存在α收敛。无论是上游地区、中游地区,还是下游地区,其标准差波动都较大,说明长江经济带各省市发展水平并不稳定。这种不稳定性,表明长江经济带沿线省市经济可持续发展的认知还存在偏差,对绿色转型的认知还不够深入。政策的非延续性及对资源环境的利用程度存在不同,导致长江经济带的省域绿色发展出现波动,这种波动主要是由于没有恰当处理好经济社会发展与资源环境保护之间的关系。尽管长江经济带沿线11省市基础和资源环境不同,发展速度和规模也存在差异,但是这种差异并没有能够在样本期内伴随着时间的推移而趋于稳定,各省份之间差异仍然存在。
(二)绝对β收敛性分析
目前,学术界将β收敛分为绝对β收敛和条件β收敛,条件β收敛主要分析不同样本是否收敛于各自的稳定水平,本文不予阐述。
绝对β收敛主要是为了研究某一变量是否在一定的时期内存在相同的发展趋势,是否将趋于最终稳态发展。本文引用绝对β收敛,主要是为了探明长江经济带省域绿色全要素生产率是否会向同一稳态水平趋同。从目前来看,长江经济带11个省市的绿色全要素生产率表现出了差异性,这种差异性既有资源禀赋的原因,但更多的是长久以来积累的内在体制机制问题。如果通过测算长江经济带省域绿色全要素生产率存在绝对β收敛,则意味着绿色全要素生产率低的省份存在向绿色全要素生产率高的省份的“追赶效应”[24]。这种“追赶效应”,意味着二者将趋于相同的稳态均衡水平。本文在Barro等[21]的文献基础上,进一步测算长江经济带省域绿色全要素生产率是否存在绝对β收敛,检验模型如下:
表3(下页)数据显示,从全国来看,省域绿色全要素生产率的β值小于0,这说明长江经济带各省市的省域绿色全要素生产率存在绝对β收敛,也就是说,各省市之间的增长差距在不断缩小。而从三大区域来看,上游、中游和下游地区的β值都小于0,即存在绝对β收敛。也就是说,存在省域绿色全要素生产率由较低省份向较高省份趋同的“追赶效应”。从稳态值来看,上游地区的稳态值最高,为0.1316,而中游地区的稳态值最低,为0.0037。从收敛速度和半生命周期数值来看,长江经济带省域绿色全要素生产率的绝对收敛速度为0.0374%,半生命周期为18.54年。而下游地区、中游地区和上游地区的绝对收敛速度分别为0.0498%、0.0323%和0.0265%,半生命周期分别为13.92年、21.24年和26.16年。根据收敛速度来看,上游地区的追赶速度更快。但是,半生命周期指标显示,上游地区的绝对收敛趋势较弱,而下游地区的绝对收敛趋势最强。这主要是由于上游地区经济基础较为薄弱,发展速度、水平和质量较中游地区和下游地区而言相对缓慢,在发展速度上虽然有很好的潜力,但是绝对收敛的速度要相对较低。该结果也同时表明,长江经济带沿线11省市之间虽然存在地区差异,但是,这种差异将在不断的波动中趋于共同发展。这主要是因为在国家提出长江经济带发展战略之后,沿线省市之间的联系度增强,长江沿线的协同发展意识不断增强,且互补性也较以往有了很大提高。各省份之间的联系日益紧密,为推动长江经济带共同发展发挥了重要作用。虽然各省市之间的差异依然存在,但是伴随着长江经济带发展战略的持续推进,各省市之间的协作不断增强,必然进一步缩小各省市之间的差距,这也是表3中长江经济带各省市存在绝对β收敛的原因。
五、研究结论与政策建议
本文针对现有定量化模型在测算省域全要素生产率时的局限,基于SBM—GML模型对长江经济带省域绿色全要素生产率和收敛性进行了测算,得到了以下结论:第一,长江经济带省域绿色全要素生产率在样本期内有效,虽然表现出短期波动,但是整体而言波动幅度不大,省域绿色全要素生产率呈逐年递增态势。同时,技术效率是影响省域绿色全要素生产率的主要原因,而规模效率指数拉低了省域绿色全要素生产率。第二,长江经济带省域绿色全要素生产率呈现较为明显的地区差异,下游地区总体优于中游和上游地区。经济越发达的地区,省域绿色全要素生产率越高。第三,长江经济带省域绿色全要素生产率并不存在显著的α收敛,但是存在绝对β收敛。即省域绿色全要素生产率在时间序列上并不具有延续性,但是,省域绿色全要素生产率低的省份存在向绿色全要素生产率高的省份的“追赶效应”,并将最终以相同的稳态趋于均衡。然而,这种“追赶效应”并不代表长江经济带发展已经找到自身合适的收敛路径。
基于上述结论,提出如下政策建议:
第一,贯彻新发展理念,推动长江经济带省域绿色转型发展。长江经济带发展作为我国重大区域发展战略,是提振区域经济发展和推动未来绿色转型的重要举措。要继续坚持以新发展理念为指导,深入推动长江经济带沿线省市实现绿色发展,在坚守生态优先的前提下,以创新驱动为引领,打造创新协同共同体,不断优化产业结构,促进产业提档升级,大力发展绿色产业,支持工业企业开展绿色转型试点,强化工业技术改造。
第二,提高规模效率,突出城市集聚效应,发挥城市群在带动区域经济增长中的作用。目前,长江经济带下游地区已经形成以长三角城市群为代表的城市规模效应,但中游地区规模效应并没有得到充分展现,上游地区规模效应也不显著。为此,长江经济带沿线城市群应该突出更强的辐射能力和影响力,这样才能够在更大范围内调动资源,实现资源的优化配置。要加快中心城市产业转型步伐,探寻新的经济增长点,发挥中心城市的示范引领作用,在继续保持技术进步的前提下,形成更大规模的城市群高质量发展。围绕不同地区的規划,促进协调发展,以实现经济又好又快发展,为长江经济带转型发展奠定基础。
第三,注重地区异质性,精准施策。不同省市的差异化发展必然要求未来经济社会发展采取不同的发展方案。这就要求长三角城市群在推进长江经济带转型发展中起到示范作用,要着眼于国内外两大市场,做强城市功能,充分发挥技术外溢效应,增强国际竞争意识,真正将发展融入国际竞争中,参与国际市场分工和新科技研发,促进产业一体化和技术转移,推动企业走出去。长江中游城市群应加强武汉城市圈、环长株潭城市群、环鄱阳湖城市群的融合发展,积极与长三角、成渝地区双城经济圈对接联动。要充分借助“一带一路”倡议,加快内陆开放型经济高地建设,进一步扩大武汉市作为经济中心的辐射带动作用,完善口岸布局,增开国际客货运航线。同时,要充分将人力资本优势转化为人才优势,增强科技创新能力,提高产业附加值,增强核心竞争力。成渝地区双城经济圈要正视目前发展中存在的短板和优势,结合资源禀赋,在筑牢长江上游生态屏障的基础上,借鉴长江经济带中游或下游地区的经验,加快推进国家重要科技创新中心建设,进一步提高现代化治理能力和治理体系建设,优化市场营商环境,提高市场运行效率,努力承接长江经济带中游地区和下游地区的产业转移,在突出品牌和特色的基础上,形成独具发展优势的产业。
参考文献
[1]黄庆华,时培豪,胡江峰.产业集聚与经济高质量发展:长江经济带107个地级市例证[J].改革,2020(1):87-99.
[2]姜旭,卢新海,龚梦琪.土地出让市场化、产业结构优化与城市绿色全要素生产率——基于湖北省的实证研究[J].中国土地科学,2019(5):50-59.
[3]王伟,孙芳城.金融发展、环境规制与长江经济带绿色全要素生产率增长[J].西南民族大学学报(人文社会科学版),2018(1):129-137.
[4]江艳婷,余华银.中国省域绿色全要素生产率空间分布差异及影响因素研究[J].合肥工业大学学报(社会科学版),2020(5):17-24.
[5]陈黎明,王俊昊,赵婉茹,等.中国区域绿色全要素生产率的影响因素及其空间特征[J].财经理论与实践,2020(4):122-132.
[6]任阳军,汪传旭,俞超.中国区域绿色全要素生产率的空间溢出效应研究[J].软科学,2019(4):40-43.
[7]韩晶,陈曦.长江经济带沿线城市绿色发展水平时空演变特征[J].华东经济管理,2021(1):24-34.
[8]李汝资,刘耀彬,王文刚,等.长江经济带城市绿色全要素生产率时空分异及区域问题识别[J].地理科学,2018(9):1475-1482.
[9]吴传清,宋子逸.长江经济带农业绿色全要素生产率测度及影响因素研究[J].科技进步与对策,2018(17):35-41.
[10]胡立和,商勇,王欢芳.工业绿色全要素生产率变化的实证分析——基于长江经济带11个省市的面板数据[J].湖南社会科学,2019(4):108-114.
[11]郑垂勇,朱晔华,程飞.城镇化提升了绿色全要素生产率吗?——基于长江经济带的实证检验[J].现代经济探讨,2018(5):110-115.
[12]MARTIN L W. WEITZMAN M L. On the welfare significance of national product in a dynamic economics[J]. Quarterly Journal of Economics, 1974(1): 156-162.
[13]石敏俊,刘艳艳.城市绿色发展:国际比较与问题透视[J].城市发展研究,2013(5):140-145.
[14]PITTMAN R W. Multilateral productivity comparisons with undesirable outputs[J]. The Economic Journal, 1983(93): 933-960.
[15]CHUNG Y H, F?魧RE R, GROSSKPF S. Productivity and undesirable outputs: a directional distance function approach[J]. Journal of Environmental Management, 1997(3): 229-240.
[16]李俊,徐晋涛.省际绿色全要素生产率增长趋势的分析——一种非参数方法的应用[J].北京林业大学学报(社会科学版),2009(4):139-146.
[17]岳鸿飞,徐颖,周静.中国工业绿色全要素生产率及技术创新贡献测评[J].上海经济研究,2018(4):52-61.
[18]杨恺钧,毛博伟,胡菡.长江经济带物流业全要素能源效率——基于包含碳排放的SBM与GML指数模型[J].北京理工大学学报(社会科学版),2016(6):54-62.
[19]FUKUYAMA H. WEBER W L. A directional slacks-based measure of technical inefficiency [J]. Socio-Economic Planning Sciences,2009(4): 274-287.
[20]OH DH. A global Malmquist-luenberger productivity index[J]. Journal of Productivity Analysis, 2010, 34(3): 183-197.
[21]BARRO R J, MANKIW N G. SALA-I-MARTIN X. Capital mobility in neoclassical models of growth[J]. The American Economic Review, 1995(1): 103-115.
[22]BARRO R J, SALA-I-MARTIN X. Technological diffusion, convergence, and growth[J]. Journal of Economic Growth, 1997, 2(1):1-26.
[23]趙磊.中国旅游全要素生产率差异与收敛实证研究[J].旅游学刊,2013(11):12-23.
[24]韩海彬,赵丽芬.环境约束下中国农业全要素生产率增长及收敛分析[J].中国人口·资源与环境,2013(3):70-76.
(责任编辑:文丰安)
