基于拧紧工艺的发动机曲轴皮带轮螺栓连接优化分析

李标，潘兰涛

(上汽通用五菱汽车股份有限公司，广西 柳州 545007)

0 引言

曲轴皮带轮螺栓是发动机五大关键螺栓之一，是曲轴、皮带轮的关键连接，承载着发动机动力传递。在实际工况下，曲轴皮带轮螺栓受力情况复杂，从而在其使用过程中常出现由于结构设计不合理或由于拧紧装配方式不正确而导致连接失效断裂等问题，严重时可以导致发动机发生故障甚至报废。因此，开展发动机曲轴皮带轮螺栓拧紧工艺研究对发动机使用的稳定性和可靠性至关重要。

由于发动机工况比较复杂，所以发动机大部分螺栓拧紧工艺都采用了转矩转角法以此获取更稳定的夹紧力。对于转矩转角法，有不少学者作了多方面的研究。汤春球等[1]通过路试验证了转矩转角法的优势，结果显示转矩转角法得到的预紧力较高，且在路试过程中预紧力衰减较少。聂晓东等[2]在星形拧紧工艺、分块拧紧工艺上作了研究，也达到了较好的螺栓预紧效果。孙贵青等[3]以发动机低压涡轮盘轴的关键连接为对象，将传统的转矩法和先进的转角法相结合，监测调整螺母的转动角度，保证了预紧力的准确控制和连接刚度的均匀一致。在发动机螺栓所受复杂载荷方面，解慧、刘文光、惠烨、王传华等[4-7]研究了螺栓松动受预紧力及外力载荷的影响规律。

在此基础上，本文以某型号发动机曲轴皮带轮螺栓失效断裂作螺栓断口分析，对曲轴皮带轮螺栓轴力及监控方式进行理论计算和验证，并设定横向振动试验验证螺栓在不同夹紧力下松动(轴力衰减)情况，寻求其衰减规律，同时做实物装配试验，验证理论计算结果及装配方法，以此优化曲轴皮带轮螺栓拧紧工艺。

1 曲轴皮带轮螺栓断裂分析

图1为螺栓断口电镜分析图；图2为腐蚀后螺栓牙边缘金相组织图；表1为螺栓硬度检测数据。

图1 螺栓断口电镜分析

图2 螺栓牙边缘金相组织(腐蚀后)50X螺栓中心金相组织(腐蚀后)400X

表1 螺栓洛氏硬度HRC检测数据

由图1可知，曲轴皮带轮螺栓受异常外力局部撕裂形成裂纹源，继而发生疲劳断裂。由图2可知，螺栓的螺牙未发现脱碳，螺栓中心组织为回火索氏体，螺栓的金相组织合格。由表1可知，螺栓硬度检测合格。由以上可判断螺栓受到异常外力作用致使螺栓产生裂纹源，继而发生疲劳断裂，故针对曲轴皮带轮螺栓松动故障作拧紧工艺分析。

2 螺栓轴力及拧紧转角理论计算

故障曲轴皮带轮螺栓拧紧工艺为扭力+转角，实际装配工艺为100N·m+70°。基于此对螺栓轴力及拧紧转角进行理论计算。

2.1 屈服点的轴力

(1)

式中：Ffy为夹紧力；σy为屈服强度；As为螺纹的应力截面积；d0为螺纹的公称应力截面积等效直径；p为螺距；d2为螺纹中径；μs为摩擦系数；α′为螺纹牙侧角。

将实测屈服强度结果：1 150～1 178MPa，摩擦系数实测平均值0.139，螺栓规格M14×1.5-6h代入公式(1)，可得到屈服点的轴力为Ffy为125～144kN，符合≥110kN的设计需求。

2.2 转角计算

(2)

图3 轴力与转角曲线图

其中：θfA为紧固转角；θfy为屈服点紧固转角；θfu为最大紧固转角；Ffy为目标紧固轴力；Tfs为初始转矩；km为平均转矩系数；δb为螺栓变形系数(柔度)；δc为配件变形系数(柔度)；p为螺距；d为公称直径。

已知Ffy=110kN，初始转矩Tfs=100N·m，螺距p=1.5。

1)由摩擦系数 0.10～0.16计算得知转矩系数为0.174～0.268，km=0.222。

2)根据提供的螺栓连接方式，计算得

δb=2.6×10-3mm/N，δc=1.5×10-4mm/N。

根据式(2)计算得θfA=90°，即转矩+转角装配方法为100N·m+90°。

相应监控窗口为：290～500N·m(屈服强度按照1 100-1 200MPa计算)。

3 螺栓松动实验验证

曲轴皮带轮螺栓连接为刚性连接，一般情况下，其静态扭力及轴力衰减较小，但由于曲轴皮带轮螺栓工况复杂，实际轴力衰减可能会较大，若拧紧工艺不合理会导致连接失效断裂等问题，故设计螺栓横向振动实验(横向振动加速轴力衰减)，验证螺栓在不同夹紧力下松动(轴力衰减)情况，寻求其衰减规律以及实物装配实验，验证理论计算结果及装配方法。图4及表2为实验过程曲轴皮带轮螺栓装配示意图及相关参数名称。

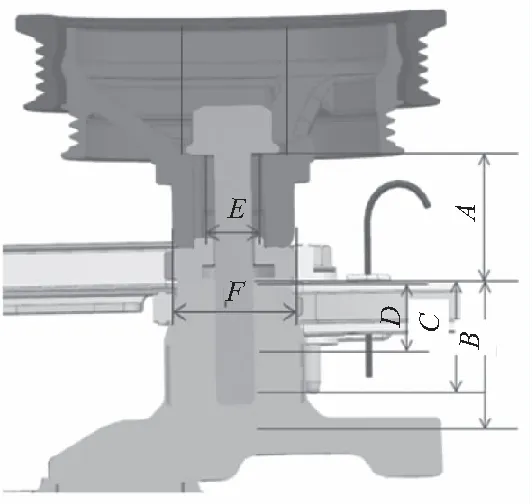
图4 曲轴皮带轮螺栓连接示意图

表2 轴皮带轮螺栓装配相关参数

3.1 横向振动实验

目的：通过横向振动实验加速轴力衰减，验证螺栓在不同夹紧力下松动(轴力衰减)情况，寻求其衰减规律。

方案：按照标准《GB/T 10431—2008 紧固件横向振动试验方法》分别在夹紧力90kN、110kN、130kN下进行横向振动试验，各取10件样品。

试验条件：横向震动试验机，自由状态下振幅±1mm，频率12.5Hz，循环周期3000次。

结果输出：螺栓轴力衰减与振动周期的关系。

3.2 实物装配实验

目的：验证理论计算结果及装配方法。

方案：在实际对手件上进行拧紧试验，检测按理论计算的装配方法拧紧后初始轴力是否符合计算要求。

试验条件：轴力试验机，实物状态拧紧。

结果输出：拧紧后的转矩、夹紧力、角度及相关曲线。

3.3 测试结果与分析

a)横向振动实验结果及分析

1)初始轴力90kN

振动周期：100次，12.5次/s，即 100/12.5=8s，其他类推。轴力衰减与振动周期关系如表3-表4所示，轴力与振动周期曲线如图5所示(本刊黑白印刷，相关疑问咨询作者)。

表3 初始轴力90 kN下轴力衰减与振动周期(100次、200次)关系

表4 初始轴力90 kN下轴力衰减与振动周期(500次、1500次)关系

图5 初始轴力90kN下轴力与振动周期曲线图

2)初始轴力110kN

轴力衰减与振动周期关系如表5-表6所示，轴力与振动周期曲线如图6所示。

表5 初始轴力110 kN下轴力衰减与振动周期(100次、200次)关系

表6 初始轴力110 kN下轴力衰减与振动周期(500次、1 500次)关系

图6 初始轴力110kN下轴力与振动周期曲线图

3)初始轴力130 kN

轴力衰减与振动周期关系如表7-表8所示，轴力与振动周期曲线如图7所示。

表7 初始轴力130 kN下轴力衰减与振动周期(100次、200次)关系

表8 初始轴力130 kN下轴力衰减与振动周期(500次、1 500次)关系

图7 初始轴力130 kN下轴力与振动周期曲线图

根据以上横向振动实验数据可知：

1)初始轴力与残余轴力呈正比关系；

2)在受切向载荷情况下，无法完全避免松动，从目前实验数据来看，没有准确得到衰减规律。

b)实物装配实验结果及分析

图8为转矩-角度-轴力关系图，表9-表10为实验数据。

图8 转矩-角度-轴力关系图

表9 转矩与轴力关系表(拧紧工艺：100N·m+70°)

表10 转矩与轴力关系表(拧紧工艺：100N·m+90°)

由实验结果可知：

1)按100N·m+70°拧紧后，螺栓轴力均值为108.3kN，不满足≥110kN的要求；

2)按100N·m+90°拧紧后，螺栓轴力均值为126.8kN，满足≥110kN的要求。

根据横向振动实验，初始轴力与残余轴力呈正比关系，在受切向载荷情况下，无法完全避免松动。从实验数据可知，没有准确得到衰减规律。在此基础上，再根据实物装配试验，得出转矩-轴力-转角的关系，曲轴皮带轮螺栓最后拧紧工艺优化为转矩转角100N·m+90°。

4 结语

针对发动机曲轴皮带轮螺栓连接失效问题，从螺栓断口分析其失效机理，并对拧紧工艺的曲轴皮带轮螺栓连接优化分析。通过对曲轴皮带轮螺栓轴力及监控方式进行理论计算和验证，设计了横向振动实验和实物装配实验。横向振动实验得出初始轴力与残余轴力呈正比关系，但无法准确得到轴力衰减规律，进而从实物装配实验中寻求转矩-轴力-转角的关系，以此优化最终的拧紧工艺，保证其连接不再发生松动疲劳失效。后续将进一步增加螺栓涂胶设计，重新验证横向振动实验，对比衰减率，以此获取更准确优化的拧紧工艺和螺栓设计，为后续工艺协同发动机设计提供参考依据。