改进卡尔曼滤波算法在动态扭矩传感器中的应用

高华东， 崔 婕

（中国航天空气动力技术研究院， 北京100074）

0 引言

动态扭矩传感器用于扭矩测量、 转速及机械功率测试等，在工业控制、测试测量、航空航天等领域均具有广泛应用。

由于机械结构的限制， 动态扭矩传感器通常采用无线供电的方式， 通过线圈耦合实现电能由定子向转子的输送，在通过整流和滤波，得到直流电压。

动态扭矩传感器的应变信号为微弱信号， 一般为0.5mV/V～2mV/V，因此在测试测量中，不可避免的受到较大干扰。 动态扭矩传感器的干扰主要有内部干扰和外部干扰。 外部干扰指外界的干扰波和环境因素如电磁干扰静电干扰， 内部干扰主要指传感器采集信号和信号模数转换的过程中以脉冲干扰的方式对信号造成误差， 还存在于所有电子器件和传输介质中以电子热振动导致的温度变化所引起的热噪声。 由于动态扭矩传感器采取线圈耦合供电的方式进行供电，周期性脉冲干扰较为严重。

对内部干扰采取软件滤波，不紧可以简化硬件电路，还可以避免硬件的二次干扰，且降低成本。 采用滑动平均滤波算法，可以消除周期性脉冲干扰和高斯噪声，但是当窗长度较短时，滤波效果不明显，窗长度较长时，延时又比较严重。 为了取得较好的滤波效果并保持较好的频率特性，对卡尔曼滤波算法进行改进，将滑动平均滤波算法与卡尔曼滤波算法进行组合的方式， 提高了动态扭矩传感器的测试精度。

1 动态扭矩传感器结构及算法设计

动态扭矩传感器由电源系统、惠斯通电桥、放大器、AD 转换、微处理器、无线发射模块及其外围电路组成，见图1。

定子供电一般为直流电源。 为了通过线圈将电能输送给转子， 需要通过逆变电路将直流电压转化为交流电压， 在转子上再通过整流滤波转化为直流电压。 该过程也是干扰产生的重要来源。

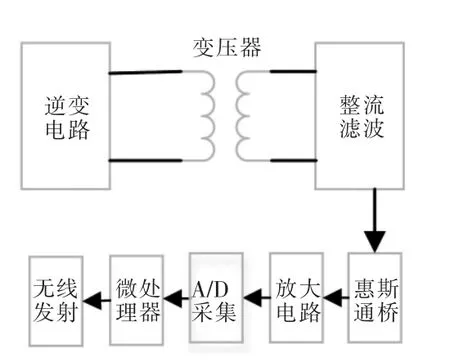
图1 动态扭矩传感器结构

惠斯通电桥将转矩信号转换为mV 级电信号， 经过放大电路处理后，由AD 采集模块进行数字化。 放大器在进行放大时，连同噪声一起放大。另外在A/D 转换模块将带有干扰的模拟信号转换为数字信号过程中会因为温度导致热噪声影响其分辨率进而影响动态扭矩传感器的精确度。

对于采集过程中的高斯白噪声或模数转化过程中产生的量化噪声，可以通过滑动平均滤波来消除。但对于非周期较大的干扰信号，滑窗滤波算法的抑制性很差。且当干扰较大时， 需要很长的窗长度才能达到理想的滤波效果，这就大大降低了频率特性。卡尔曼滤波算法也能消除白噪声和周期性干扰脉冲，但对于非周期干扰脉冲，会引入线性误差。

为了有效滤除周期性脉冲干扰、非周期性脉冲干扰、高斯白噪声、量化噪声等，对卡尔曼滤波算法进行改进，见图2。

图2 改进卡尔曼滤波算法

首先采用阈值滤波算法， 对偶然因素引起的脉冲干扰进行剔除。对于循环采样，将更新的采样值与对比值之差与系统所允许的最大差值来进行比较。 当在允许范围内时，该次采样有效，当超过允许范围，该次采样用对比值来代替。

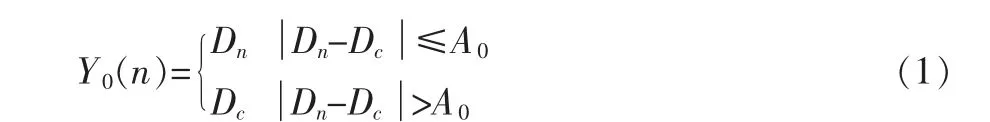
式中：Dn—该次采样值；Dc—对比值，由滑窗滤波器给出；A0—系统允许的采样值与对比值的最大差值。

经过阈值滤波器处理后的数据Y0（n）进入滑窗滤波器进行平滑。 规定窗口长度M，按照先入先出原则，每次增加一个数， 然后去掉一个最老的数， 数目总数保持M不变。 然后对这M 个数求平均数。 数学表达式为：

该波器输出的信号去往阈值滤作为对比值Dc， 并作为下一级卡尔曼滤波器的输入。

卡尔曼滤波器的基本结构见图3。

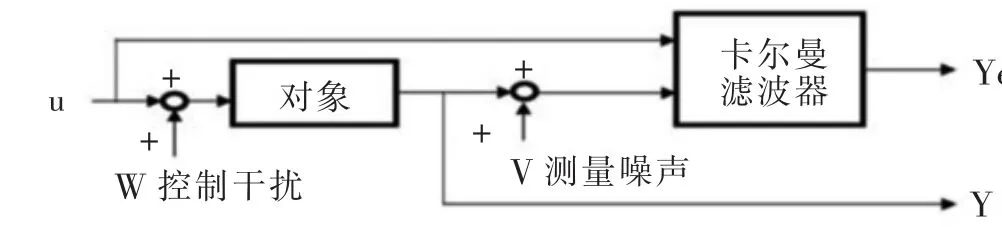
图3 卡尔曼滤波器的基本结构

卡尔曼滤波器的实质就是， 将实际信息与测量信息有机融合，从而得到最大概率的控制量。 对于一个线性离散系统，其状态空间方程为：

式中：H—测量系统的参数， 对于多测量系统而言，H—矩阵。 W（k）和V（k）—表示过程和测量的噪声。 他们被假设成高斯白噪声（White Gaussian Noise），他们的协方差（covariance）分别是Q，R（这里我们假设他们不随系统状态变化而变化）。

卡尔曼滤波器的实现由以下五个公式组成：

组合预测值和观测值，得到最优估计值；Z（k）—观测值。 对于该系统，

2 试验测试

试验中，采用的动态扭矩传感器量程为500Nm，满量程信号输出为0.5mV/V。 AD 采集模块选用了24 位高集成度芯片AD7192，该芯片内部集成了PGA，最大放大倍数为128 。 为了提高标定精度，采用砝码作为负载，通过静态标定的方式得到标定数据， 同一力矩下， 每隔1min记录一次数据，共计三次。 滤波前后试验数据见表1。

表1 滤波前后试验数据

3 结论

测试结果见图4。

图4 滤波前后试验结果图

根据上图可到以下结论：

（1）滤波后，传感器线性度、重复性明显优于滤波前；

（2）滤波后，传感器的精度更加精确；

（3）滤波后，传感器的稳定度更高。