一类双圈图的匹配能量和Hosoya指标排序

马海成，李丹阳，解承玲

(青海民族大学数学与统计学院，青海 西宁 810007)

1 预备知识

本文仅考虑有限无向的简单图.设G是有n个点的图，G的一个匹配是指G的一个生成子图，它的每个连通分支是孤立点或者孤立边.恰有k条边的匹配称为k-匹配.在文献[1]中图G的匹配多项式定义为：

这里m(G,k)是G中k-匹配的数目，且约定m(G,0)=1.为了方便，本文中将μ(G，x)简记为μ(G).

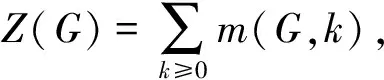
定义1设λ1，λ2,…，λn是图G的匹配多项式的所有根，定义它的匹配能量为

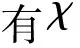
设G是一个图，以V(G)和E(G)分别表示图G的点集和边集.如果e∈E(G),以Ge表示从图G中删去边e后得到的图.如果V1⊆V(G)，以GV1表示从图G中删去V1中的所有点以及和这些点关联的所有边后得到的图.如果V1={u}，将G(〗u}简记为Gu.以G∪H表示两个图G和H的并图.以Pn，Cn，Kn分别表示n个点的路、圈和完全图.路Ps+2的两个端点分别与圈Ca+1和Cb+1上的一个点黏结后得到的连通图称为哑铃图(见图1)，记为∞(a，s，b)，这里的s≥0,a≥2,b≥2.路Ps+1的一个端点与圈Ca+1上的一个点黏结后得到的a+s+1个点的连通图称为Q-图，记为Q(a，s)，这里的s≥0,a≥2.以P(s，t)表示Ps∪Pt.文中没有说明的记号和术语参见文献[1].

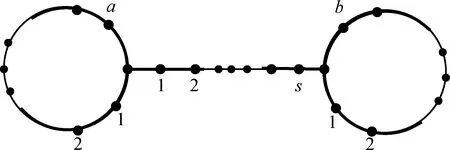
图1 哑铃图∞(a，s，b)Fig.1 The dumbbell shape graph ∞(a,s,b)

2 若干引理

引理1[1]设图G有k个连通分支G1,G2,…,Gk，则

μ(G,x)=μ(G1,x)μ(G2,x)…μ(Gk,x).

引理2[1]设G是一个图，u∈V(G)，e=uv∈E(G)，则

EM(G)=2π∫+∞01x2ln[∑k≥0m(G,k)x2k]dx,

这里m(G,k)是G中k-匹配的数目.

由引理5,规定一种偏序关系“⪯”.设G1和G2是两个n阶图，对所有的非负整数k,若满足m(G1，k)≤m(G2，k)，则定义G1⪯G2.若不等式m(G1，k)≤m(G2，k)对某个非负整数k是严格的，则定义G1G2.于是，由引理5可以得到下面的结果：

G1⪯G2⟹EM(G1)≤EM(G2),Z(G1)≤Z(G2)；

G1G2⟹EM(G1)

引理6[13]设G1和G2是两个n阶图，如果存在一个m阶图H,满足

μ(G1)-μ(G2)=μ(H),

则：

(i)n-m是一个偶数；

(ii) 如果n-m≡0(mod 4),则G1≻G2；

(iii) 如果n-m≡2(mod 4),则G1G2.

设H是一个m阶的图，f(x)是一个多项式(它未必是一个图的匹配多项式)，如果f(x)与μ(H)有相同的形式，即

这里的ak≥0,且至少有一个ak>0,记f(x)≈μ(H).

众所周知，对于图G1和G2，多项式μ(G1)-μ(G2)一般不是一个图的匹配多项式，但若存在一个m阶的图H,使得μ(G1)-μ(G2)≈μ(H)，则引理6的结论也成立，这就是下面的引理7.

引理7设G1和G2是两个n阶图，且μ(G1)-μ(G2)≠0，如果存在一个m阶图H,满足

μ(G1)-μ(G2)≈μ(H),

则：

(i)n-m是一个偶数；

(ii) 如果n-m≡0(mod 4)，则G1≻G2；

(iii) 如果n-m≡2(mod 4)，则G1G2.

(ii) 不妨设n=m+4k,

μ(G1)=xn-m(G1,1)xn-2+…+m(G1,2k)xm-

m(G1,2k+1)xm-2+…，

μ(G2)=xn-m(G2,1)xn-2+…+m(G2,2k)xm-

m(G2,2k+1)xm-2+…，

f(x)=a0xm-a1xm-2+….

由于μ(G1)=μ(G2)+f(x)，比较系数得

所以G1≻G2.

(iii) 不妨设n=m+4k+2，

μ(G1)=xn-m(G1,1)xn-2+…-m(G1,2k+

1)xm+m(G1,2k+2)xm-2-…，

μ(G2)=xn-m(G2,1)xn-2+…-m(G2,2k+

1)xm+m(G2,2k+2)xm-2-…，

f(x)=a0xm-a1xm-2+….

由于μ(G1)=μ(G2)+f(x),比较系数得

所以G1G2.

3 主要定理及证明

引理8(i) 设a≤b,则μ(Pa∪Q(b，s))-μ(Pa-2∪Q(b+2,s))=μ(P1∪Q(b-a+1,s))；

(ii) 设4≤a≤b,则μ(∞(a，s，b))-μ(∞(a-2,s,b+2))≈-μ(P1∪Q(b-a+2，s)).

证明(i) 由引理2(ii)，

μ(Q(b，s))=μ(Pb+s+1)-μ(Pb-1∪Ps)，

由引理4,

μ(Pa∪Q(b,s))-μ(Pa-2∪Q(b+2,s))=

[μ(P(a,b+s+1))-μ(P(a-2,b+s+3))]-

[μ(P(a,b-1))-μ(P(a-2,b+1))]μ(Ps)=

μ(P(1,b+s-a+2))-μ(P(1,b-a))μ(Ps)=

μ(P1∪Q(b-a+1,s)).

(ii) 由引理2(i)，

μ(∞(a，s，b))=xμ(Pa∪Q(b，s))-

2μ(Pa-1∪Q(b，s))-μ(Pa∪Q(b，s-1))，

μ(∞(a-2，s，b+2))=xμ(Pa-2∪Q(b+2，

s))-2μ(Pa-3∪Q(b+2，s))-

μ(Pa-2∪Q(b+2,s-1)),

由(i)和引理2知，

μ(∞(a,s,b))-μ(∞(a-2,s,b+2))=

x[μ(Pa∪Q(b，s))-μ(Pa-2∪Q(b+2,s))]-

2[μ(Pa-1∪Q(b,s))-μ(Pa-3∪Q(b+2,s))]-

[μ(Pa∪Q(b,s-1))-μ(Pa-2∪Q(b+2,

s-1))]=xμ(P1∪Q(b-a+1,s))-

2μ(P1∪Q(b-a+2,s))-μ(P1∪Q(b-a+

1,s-1))=μ(P1∪Q(b-a+1,s+1))-

2μ(P1∪Q(b-a+2,s))=μ(P1)[μ(Q(b-

a+1,s+1))-μ(Q(b-a+2,s))]-

μ(P1∪Q(b-a+2,s))=μ(P1)[(μ(Pb+s-a+3)-

μ(Pb-a∪Ps+1))-(μ(Pb+s-a+3)-

μ(Pb-a+1∪Ps))]-μ(P1∪Q(b-a+2,s))=

μ(P1)[μ(P(b-a+1,s))-μ(P(b-a,s+1))]-

μ(P1∪Q(b-a+2，s)).

1) 若s≥b-a+1,由引理4知，μ(P(b-a+1,s))-μ(P(b-a,s+1))=μ(Ps-b+a-1)，则

μ(∞(a，s，b))-μ(∞(a-2，s，b+2))=

μ(P1)[μ(Ps-b+a-1)-μ(Q(b-a+2，s)].

图Q(b-a+2，s)的点数N=b-a+s+3,路Ps-b+a-1的点数N1=s-b+a-1,N-N1=2(b-a)+4,即从图Q(b-a+2，s)中删去一条路P2(b-a)+4后便得到路Ps-b+a-1.路P2(b-a)+4上有一个完美匹配(即饱和了所有点的匹配)，于是路Ps-b+a-1上的任何一个k匹配，并上路P2(b-a)+4的完美匹配后便得到图Q(b-a+2，s)上的一个k+b-a+2匹配，故m(Ps-b+a-1，k)≤m(Q(b-a+2，s)，k+b-a+2).

由于

b-a+2)xN1-2k，

(1)

所以

μ(Q(b-a+2，s))-μ(Ps-b+a-1)=

a+2)-m(Ps-b+a-1,k)]xN1-2k.

(2)

结合不等式m(Ps-b+a-1,k)≤m(Q(b-a+2,s),k+b-a+2)),比较多项式μ(Q(b-a+2，s))-μ(Ps-b+a-1) 和多项式μ(Q(b-a+2，s))，即式(1)和式(2)，发现它们有完全一样的形式.只是当b-a+2为偶数时，多项式μ(Q(b-a+2,s))-μ(Ps-b+a-1)中项xN1-2k的系数比多项式μ(Q(b-a+2,s))中项xN1-2k的系数的绝对值会减少，符号仍然与多项式μ(Q(b-a+2,s))的项xN1-2k符号相同；当b-a+2为奇数时，多项式μ(Q(b-a+2,s))-μ(Ps-b+a-1)中项xN1-2k的系数比多项式μ(Q(b-a+2，s))中项xN1-2k的系数的绝对值会增加，符号仍然与多项式μ(Q(b-a+2，s))的项xN1-2k符号相同.也就是说，μ(Q(b-a+2,s))-μ(Ps-b+a-1)≈μ(Q(b-a+2,s))，于是μ(∞(a,s,b))-μ(∞(a-2,s,b+2))≈-μ(P1∪Q(b-a+2,s)).

2) 若s=b-a,此时μ(P(b-a+1,s))-μ(P(b-a,s+1))=0，则μ(∞(a,s,b))-μ(∞(a-2,s,b+2))=-μ(P1)μ(Q(b-a+2,s).

3) 若s≤b-a-1,由引理4知，此时μ(P(b-a+1,s))-μ(P(b-a,s+1))=-μ(Pb-a-s-1)，则

μ(∞(a,s,b))-μ(∞(a-2,s,b+2))=

μ(P1)[-μ(Pb-a-s-1) -μ(Q(b-a+2,s)].

图Q(b-a+2，s)的点数N=b-a+s+3,路Pb-a-s-1的点数N2=b-a-s-1,N-N2=2s+4,即从图Q(b-a+2,s)中删去一条路P2s+4后便得到路Pb-a-s-1.路P2s+4上有一个完美匹配，于是路Pb-a-s-1上的任何一个k匹配，并上路P2s+4的完美匹配后便得到图Q(b-a+2,s)上的一个k+s+2匹配，故m(Pb-a-s-1,k)≤m(Q(b-a+2,s),k+s+2).

由于

2)xN2-2k，

(3)

所以

μ(Q(b-a+2，s))+μ(Pb-a-s-1)=

2)+m(Pb-a-s-1,k)]xN2-2k.

(4)

结合不等式m(Pb-a-s-1，k)≤m(Q(b-a+2，s)，k+s+2),与1)类似，得到μ(Q(b-a+2,s)+μ(Pb-a-s-1)≈μ(Q(b-a+2,s),于是μ(∞(a，s,b))-μ(∞(a-2,s,b+2))≈-μ(P1∪Q(b-a+2,s)).

引理9(i)μ(P2k∪Q(2k,s))-μ(P2k-1∪Q(2k+1,s))=μ(Ps+1)；

(ii)μ(P2k-1∪Q(2k,s))-μ(P2k-2∪Q(2k+1,s))=μ(Ps+2)-μ(Ps)；

(iii)μ(∞(2k，s，2k))-μ(∞(2k-1,s,2k+1))≈-μ(Cs+2).

证明(i) 由引理2(ii),μ(P2k∪Q(2k,s))=μ(P2k∪P2k+s+1)-μ(P2k∪P2k-1∪Ps)，μ(P2k-1∪Q(2k+1,s))=μ(P2k-1∪P2k+s+2)-μ(P2k-1∪P2k∪Ps)，由引理4,μ(P2k∪Q(2k,s))-μ(P2k-1∪Q(2k+1,s))=μ(Ps+1).

(ii) 由引理2(ii)，μ(P2k-1∪Q(2k，s))=μ(P2k-1∪P2k+s+1)-μ(P2k-1∪P2k-1∪Ps)，μ(P2k-2∪Q(2k+1,s))=μ(P2k-2∪P2k+s+2)-μ(P2k-2∪P2k∪Ps)，由引理4,μ(P2k-1∪Q(2k,s))-μ(P2k-2∪Q(2k+1,s))=μ(Ps+2)-μ(Ps).

(iii) 由引理2(i)，μ(∞(2k，s，2k))=xμ(P2k∪Q(2k，s))-2μ(P2k-1∪Q(2k，s))-μ(P2k∪Q(2k,s-1)),μ(∞(2k-1,s,2k+1))=xμ(P2k-1∪Q(2k+1,s))-2μ(P2k-2∪Q(2k+1,s))-μ(P2k-1∪Q(2k+1,s-1)).

由(i)和(ii)知，μ(∞(2k，s，2k))-μ(∞(2k-1，s，2k+1))=xμ(Ps+1)-2(μ(Ps+2)-μ(Ps))-μ(Ps)=-μ(Ps+2)+2μ(Ps)=-μ(Cs+2)+μ(Ps).

圈Cs+2上删去一个P2便得到路Ps,而P2有完美匹配，同引理8的证明类似，得到-μ(Cs+2)+μ(Ps)≈-μ(Cs+2).

引理10(i)μ(P2k+1∪Q(2k+1,s))-μ(P2k∪Q(2k+2,s))=μ(Ps+1)；

(ii)μ(P2k∪Q(2k+1,s))-μ(P2k-1∪Q(2k+2,s))=μ(Ps+2)-μ(Ps)；

(iii)μ(∞(2k+1,s, 2k+1))-μ(∞(2k，s,2k+2))≈-μ(Cs+2).

证明与引理9类似，略.

定理1设s是一个固定的非负整数，对图∞(a，s，b),有：

(i) 当a+b=4k,∞(3，s, 4k-3)≻∞(5，s,4k-5)≻…≻∞(2k-1,s,2k+1)≻∞(2k，s,2k)≻∞(2k-2,s,2k+2)≻…≻∞(4，s,4k-4)≻∞(2，s,4k-2);

(ii) 当a+b=4k+1,∞(3，s,4k-2)≻∞(5，s,4k-4)≻…≻∞(2k-1,s,2k+2)≻∞(2k+1,s,2k)=∞(2k，s,2k+1)≻∞(2k-2,s,2k+3)≻…≻∞(4，s,4k-3)≻∞(2，s,4k-1);

(iii) 当a+b=4k+2,∞(3，s,4k-1)≻∞(5，s,4k-3)≻…≻∞(2k-1,s,2k+3)≻∞(2k+1,s,2k+1)≻∞(2k，s,2k+2)≻…≻∞(4，s,4k-2)≻∞(2，s,4k);

(iv) 当a+b=4k+3,∞(3，s,4k)≻∞(5，s,4k-2)≻…≻∞(2k+1,s,2k+2)≻∞(2k+3,s,2k)=∞(2k,s,2k+3)≻∞(2k-2,s,2k+5)≻…≻∞(4,s,4k-1)≻∞(2，s,4k+1).

证明由引理8(ii)，当4≤a≤b,有

μ(∞(a,s,b))-μ(∞(a-2,s,b+2))≈

-μ(P1∪Q(b-a+2,s)).

(5)

等式(5)左端的每个图的点数为a+b+s+2,右端的图的点数为b+s-a+4，它们的差为2a-2.于是由引理7知，当a为奇数时有∞(a-2，s，b+2))≻∞(a，s，b)，当a为偶数时有∞(a-2，s，b+2))∞(a，s，b),由此便得到(i)～(iv)中的不等式的前半段和后半段.

由引理9(iii)知，

μ(∞(2k，s，2k))-μ(∞(2k-1,s,2k+1))≈

-μ(Cs+2).

(6)

等式(6)左端的每个图的点数为4k+s+2,右端图的点数为s+2,它们的差为4k.于是由引理7，得到定理1(i)中间的偏序关系∞(2k-1，s，2k+1)≻∞(2k，s，2k).

类似地，由引理10(iii)知，

μ(∞(2k+1,s,2k+1))-μ(∞(2k，s，2k+2))≈

-μ(Cs+2).

(7)

等式(7)左端的每个图的点数为4k+s+4,右端的图的点数为s+2，它们的差为4k+2.于是由引理7，得到定理1(iii)中间的偏序关系∞(2k+1,s,2k+1)≻∞(2k，s，2k+2).定理证毕.

下面的3个推论是定理1的直接推论.

推论1设s是一个固定的非负整数，对图∞(a，s，b),有：

(i) 当a+b=4k,EM(∞(3,s，4k-3))>EM(∞(5,s,4k-5))> …>EM(∞(2k-1,s,2k+1))>EM(∞(2k，s，2k))>EM(∞(2k-2，s，2k+2))>…>EM(∞(4，s，4k-4))>EM(∞(2，s，4k-2));

(ii) 当a+b=4k+1，EM(∞(3，s，4k-2))>EM(∞(5，s，4k-4))>…>EM(∞(2k-1，s，2k+2))>EM(∞(2k+1，s，2k))=EM(∞(2k，s，2k+1))>EM(∞(2k-2，s，2k+3))>…>EM(∞(4，s，4k-3))>EM(∞(2，s，4k-1));

(iii) 当a+b=4k+2，EM(∞(3，s，4k-1))>EM(∞(5，s，4k-3))>…>EM(∞(2k-1，s，2k+3))>EM(∞(2k+1，s，2k+1))>EM(∞(2k，s，2k+2))>…>EM(∞(4，s，4k-2))>EM(∞(2，s，4k));

(iv) 当a+b=4k+3，EM(∞(3，s，4k))>EM(∞(5，s，4k-2))>…>EM(∞(2k+1，s，2k+2))>EM(∞(2k+3，s，2k))=EM(∞(2k，s，2k+3))>EM(∞(2k-2，s，2k+5))>…>EM(∞(4，s，4k-1))>EM(∞(2，s，4k+1)).

推论2设s是一个固定的非负整数，对图∞(a，s，b),有：

(i) 当a+b=4k，Z(∞(3，s，4k-3))>Z(∞(5，s，4k-5))>…>Z(∞(2k-1，s，2k+1))>Z(∞(2k，s，2k))>Z(∞(2k-2，s，2k+2))>…>Z(∞(4，s，4k-4))>Z(∞(2，s，4k-2));

(ii) 当a+b=4k+1，Z(∞(3，s，4k-2))>Z(∞(5，s，4k-4))>…>Z(∞(2k-1，s，2k+2))>Z(∞(2k+1，s，2k))=Z(∞(2k，s，2k+1))>Z(∞(2k-2，s，2k+3))>…>Z(∞(4,s，4k-3))>Z(∞(2,s，4k-1));

(iii) 当a+b=4k+2，Z(∞(3，s，4k-1))>Z(∞(5，s，4k-3))>…>Z(∞(2k-1，s，2k+3))>Z(∞(2k+1，s，2k+1))>Z(∞(2k，s，2k+2))>…>Z(∞(4，s，4k-2))>Z(∞(2，s，4k));

(iv) 当a+b=4k+3,Z(∞(3,s，4k))>Z(∞(5,s，4k-2))>…>Z(∞(2k+1，s，2k+2))>Z(∞(2k+3，s，2k))=Z(∞(2k，s，2k+3))>Z(∞(2k-2，s，2k+5))>…>Z(∞(4,s,4k-1))>Z(∞(2,s,4k+1)).

推论3在s和a+b=c固定的哑铃图∞(a，s,b)图中，匹配能量最大的图是∞(3,s，c-3),最小的图是∞(2,s，c-2);Hosoya指标最大的图是∞(3,s，c-3),最小的图是∞(2,s,c-2).

注3本文给出了哑铃图∞(a，s，b)在s不变而a和b两个变量变化下匹配能量的全排序和Hosoya指标的全排序.如果让3个变量a、s和b都变化，如何给出哑铃图∞(a，s，b)匹配能量的全排序将很复杂，有待进一步探讨.