合放交通流条件下城市交叉口通行能力研究

白 翰，张康宇，王修光，燕 翔，冯启龙

(山东交通学院 交通与物流工程学院，山东 济南 250357)

0 引 言

交叉口作为城市道路中重要的交通组织形式，对其通行能力进行研究在城市交通管理与控制、交通规划与设计等方面占有重要地位[1]。现在很多学者研究了传统十字路口的通行能力[2-7]，其中魏恒等[2]提出了路段上“自行车流”行驶状态与其通行能力间的定量分析方法，并建立了信号交叉口“自行车流”行驶状态与通行能力计算模型；D.P.ALLEN等[3]通过自行车交通量与自行车与右转机动车间冲突区域的绿灯相位百分比间的关系，确定自行车饱和流量调整系数，以计算交叉口处自行车道通行能力；M.HOSSAIN等[4]采用坐标法模拟车辆位置，从而确定混合交通条件下车道通行能力与交通流、车道宽度和交通组成间的定量关系；韩凤春等[5]从交叉口宏观和微观特性出发，进行了混合交通流动态模拟系统及其通行能力分析模型的建立；周溪召等[6]以当量人群描述非机动车和行人对机动车通行的共同影响，确定了无控制交叉口车道右转、直行及左转的通行能力；何瑞等[7]从信号控制人行横道处研究行人过街对城市道路通行能力的影响，在行人通过斑马线的情形下，建立了道路通行能力的分析方法。也有学者构建了十字路口通行能力的计算模型[8-11]，如CJJ 37—90《城市道路设计规范》中的推荐经典方法；杨佩昆等[9]提出的冲突点法；刘美岐等[10]建立了红灯右转和右转滞后放行信号控制条件下的信号交叉口直右共用车道通行能力模型；李素兰等[11]研究了信号控制交叉口的车辆优先权规则和信号周期内不同时刻的车辆更新规则,构建了一个平面十字信号控制交叉口元胞自动机模型。

然而，国内外许多文献大多都提到混合交通环境下的通行能力，其主要基于行人、非机动车、道路宽度、信号周期、车辆构成等因素对通行能力的分析研究，且大部分在研究混合交通流通行能力时较少考虑车与车间的影响，缺乏合放交通流的通行能力的计算方法。

基于此，笔者考虑交通实体间的冲突规律[12]、合放交通流特性，利用可穿越间隙理论与经典信号控制交叉口通行能力计算方法进行城市交叉口合放交通流通行能力的研究，从而建立合放交叉口通行能力综合计算模型，并对交叉口转向比例、车道宽度、慢行交通影响系数进行修正[13]，为城市管理者获取更为准确和简便的交叉口通行能力提供了理论支撑。

1 交叉口合放交通流特性分析

交叉口信号控制和非信号控制的过渡状态是交叉口合放，就十字路口相交道路而言是信号控制，即受被交道路车辆绿灯通行时间的影响，相交道路车流需停车等待；而对于合放的对向进口是无信号控制，即不同方向车流同时放行，不受信号控制，且存在让行规则。

1.1 直行交通流

合放时直行交通流需要损失部分启动时间，以高密度队列式通过进口道停车线，最终安全到达出口道，期间直行车流不仅会受到单位周期内绿灯时长限制和直行车道与其他方向车流共用同一车道时的干扰影响，同时受到对向左转车流的交通冲突的影响，主要体现在直行与左转车流的冲突时间、冲突面积以及冲突数量等方面，冲突特征越明显，其对直行交通流通行能力影响则会越大。

1.2 左转交通流

合放时左转交通流，常布置在交叉口进口道左侧，以直左、左转专用和直左右共用车道等形式存在，相较于承担多种交通功能的混合车道的左转车流，专用左转车流的车头时距要小，车道功能明确，前后车前后方向性干扰要弱。故合放过程中，专用左转车流与对向直行车流产生冲突时，直行车流优先于左转车流通行，且其能够借助直行车流空隙穿行通过，与无信号交叉口主路车流优先通行的基本特征一致。而对于承担多种交通功能的混合车道中的左转车流而言，其受到前后车运行状态的影响显著(如前车左转、后车直行，或前车直行、后车左转)，同时在对向直行情况下，其所受影响也较突出。

1.3 右转交通流

合放时右转交通流分布在进口右侧，以右转专用道、直右(直左右)车道等形式存在，通常不遵循信号灯指示通过，主要受混行车道中直行或左转车辆的方向性干扰，即在直行和右转共同使用车道或直行左转右转共同使用车道中，会出现前车因等待绿灯而阻挡后方右转弯转车辆的情况，从而致使右转弯转车流发生中断。

2 合放通行能力计算模型构建

2.1 模型假设

1)在信号周期期间，确保相反进口在相同相位释放，满足左转弯和直行车辆之间部分冲突的条件；

2)交叉口交叉形式为正交，进口停车线位置、车道数目及其功能与对向进口对称，且保证转弯半径、车道宽度等几何尺寸一致；

3)保证交叉口各交通参与者安全与规则意识良好，车辆不受交通秩序干扰，且驾驶员驾驶技术良好，驾驶操作行为良好；

4)当前交叉口包括平整度、各类病害等路面条件良好，周边交通环境与天气环境良好。

2.2 模型提出

根据停车线法通行能力计算方法与CJJ 37—90《城市道路设计规范》的相关理论，并结合交通冲突因素分析进行模型构造。笔者从单车道通行能力计算入手，引入交通冲突复杂系数、左转补偿效益理念，来提高基本通行能力计算精度，同时进一步推广至单进口道通行能力计算，以此来满足不同城市道路合放交叉口车道布局场景下的通行能力计算需求，计算模型如下。

2.2.1 直行(直左)交通流通行能力

1)基本公式

按照交叉口处有呈现周期性分布的信号控制规律，根据单周期内的饱和流率进行计算，每个信号周期内单条直行车道通行能力计算qis，如式(1)：

(1)

式中：i为交叉口进口编号，即第i个合放进口；ns为直行(直左)车道数；tg为信号周期内绿灯时间,s；t0为当信号灯色转为绿色的时刻起，第一辆车启动并驶过停车线所花费的时间，s；ti为直行(直左)或右转车辆驶过停止线的平均间隔时间，s/pcu；Ψ为直行车道通行能力折减系数，取0.9；FC为交通冲突复杂系数；β′ij为第i个进口道的第j个直左车道中左转车流所占比例，若为直行车道β′ij取0。

2)模型修正

参照交通实体间的冲突规律,并结合合放交通流下各种交通流的冲突复杂程度与直行车流的交通特性，从而规定交通冲突区域：即十字交叉口内部中相互干扰或冲突的车流i和车流j，根据各车流所在的车道宽度所规定的带状区域的面积为Si、Sj，从其形成交集点起，直至交通流冲突结束或完成结束分合流过程为止，该区域即为冲突区域即Si∩Sj，两股车流所形成的总面积为Si∩Sj，如图1。

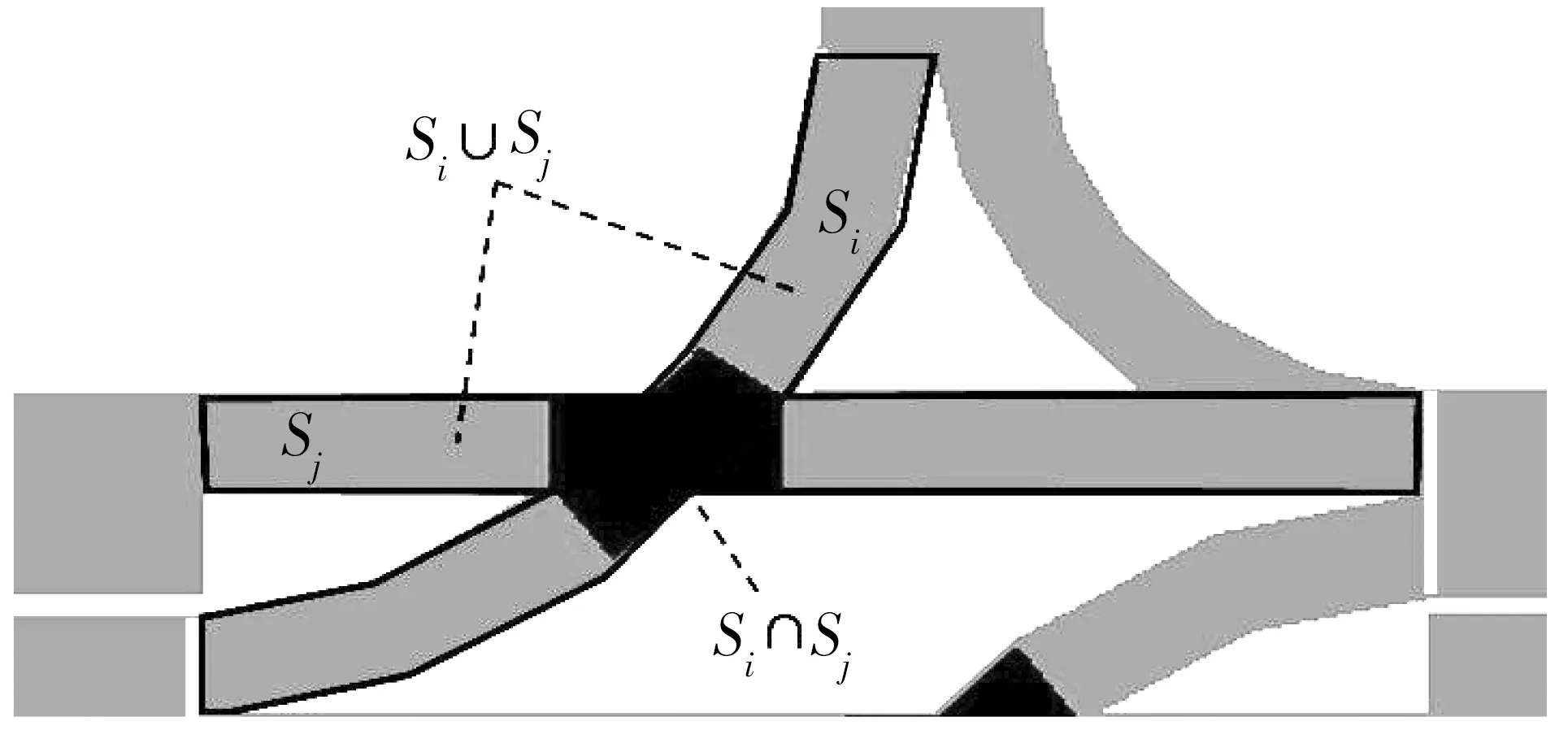
图1 冲突区域Fig.1 Schematic diagram of conflict areas

在交叉口内部不同方向的交通流彼此冲突时，其通行能力的高低与冲突点个数及角度也相关，相互冲突的车流同时放行时，其中在冲突点N处，车流i和车流j彼此冲突，其角度为αi,j，那么存在函数f(αi,j)，满足各冲突点车流冲突关系。

合放交叉口的交通冲突复杂系数FC，如式(2)、式(3)：

(2)

(3)

式中：k为彼此冲突的交通流组合序号；Dk为在交叉路口冲突交通流组合k中，其所包括的交通流个数；i,j为彼此冲突的交通流序号；Ai,j为冲突优先指数，表征交通流i对交通流j的优先程度；qi为交通流i的交通量；ts,i为交通流i的车辆在冲突区域上方的平均时间；ta,i为交通流i的车辆占用冲突区域之前，已阻挡交通流的时间前置量。

2.2.2 左转交通流通行能力

1)基本公式

由合放交通特性的分析可知，依据可穿越间隙理论，认为借机穿越直行车道车流的左转车道车流的通行能力可参考无信号交叉口次要道路通行能力计算方法，直行车流可看作无信号交叉口主要道路通行能力。因此，在合放交通流中，直行与左转同时放行时，进口道的单条左转车道通行能力qil计算，如式(4):

(4)

式中：qjs为编号为j的对向直行车道的交通量，pcu/h；qil为编号为i的同向左转车道的交通量，pcu/h；q为主要道路交通流量，pcu/h；nl为左转车道数；t′0为临界间隙时间，s；t为对向直行车辆跟驰行驶的车头时距，s。

2)模型修正

考虑到在转换不同信号相位时车辆驶入冲突点的先后位置的顺序不同，则左转弯车辆将提前进入交叉口，并抵达冲突点所在的位置，前置量影响与进口道停车线及交叉口转弯半径等因素有关，冲突时间的计算式(5)：

(5)

式中：L1为直行车道头车到达冲突点的距离；L2为左转车道头车到达冲突点的距离；v1为直行车道头车到达冲突点的速度；v2为左转车道头车到达冲突点的速度。

(6)

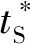
2.2.3 右转交通流通行能力

根据右转弯车辆往往不由信号相位控制，无论是传统四相位或是混合放行的方式，所呈现的交通属性基本相近，当前交通流与其他方向交通流都通过分流和合流点体现，造成的冲突点数目为0，从而一条右转弯车道的通行能力需依据具有信号控制设施的路口右转弯车道的通行能力qir测算如式(7):

(7)

式中：nr为右转车道数。

2.3 各类交通流通行能力计算模型(A-F)

笔者通过对合放交通流特性的分析，并考虑同向与对向进口道的各类交通功能的车道数目将城市交叉口合放车流冲突种类划分为A-F类，具体可见表1。

表1 城市交叉口合放交通流冲突种类划分Table 1 Classification of mixed release of traffic flow conflicts at urban inte-rsections

2.3.1 一直左穿行一直左(A类)

该类合放车流的直行与左转车流共道行驶，在行驶方向上前后车受方向性约束较大，直行车辆易受前方左转车辆阻碍而造成车辆停车。其通行能力基本计算方法与具有信号控制设施的路口左转直行右转的通行能力具有同一性。所以，对于i进口道基本通行能力为一条直行车道与一条左转车道通行能力的叠加，具体计算如式(8)。同一相位放行状况与几何布局如图2。

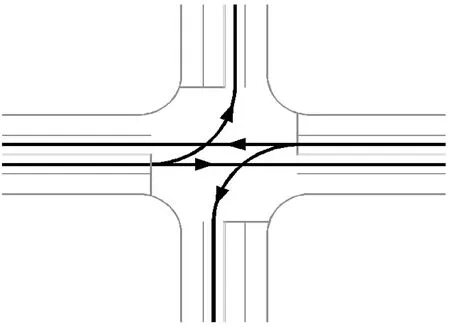
图2 A类合放交叉口车道布局Fig.2 Lane layout of class A mixed release intersection

(8)

2.3.2 一左转穿行一直行(B类)

该类合放车流的左转车流与直行(直右)车流分别在各自车道行驶，前后车的方向性约束较小，且直行车流通行优先级高于左转车流，直行车流可优先通行，左转车流利用直行车流空隙通行，此时直行(直行右转)车流可等价具备信号控制设施的路口的直行车道交通流，且反方向的左转弯车辆会干扰对当前车流造成影响。所以，对于i进口道基本通行能力为一条左转车道与一条直行车道通行能力的叠加，具体计算如式(9)。同一相位放行状况与几何布局如图3。

图3 B类合放交叉口车道布局Fig.3 Lane layout of class B mixed release intersection

(9)

2.3.3 一直左穿行直行+直左(C类)

该类合放车流的直左车流与直行车流分别在各自车道行驶，直左车流不仅受到前后车的方向约束，且受到对向直行车道车流的冲突影响。所以，当直行左转车道设置时，其具备信号控制路口直左混行车道的条件。因此，对于i进口基本通行能力为一条直行车道与一条直左车道通行能力的叠加，具体计算如式(10)。同一相位放行状况与几何布局如图4。

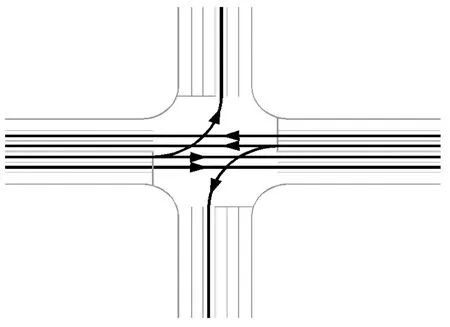
图4 C类合放交叉口车道布局Fig.4 Lane layout of class C mixed release intersection

(10)

2.3.4 一左转穿行两直行(D类)

由于直行车流通行权优于左转，可优先通行，且存在两股直行车流，该类的左转车流需连续穿越两股直行车流，导致其一次性通过交叉口的机会减少，对直行车流的影响增大。所以，对于i进口道的基本通行能力为两条直行车道与左转最大通过量的叠加，具体计算如式(11)。同一相位放行状况与几何布局如图5。

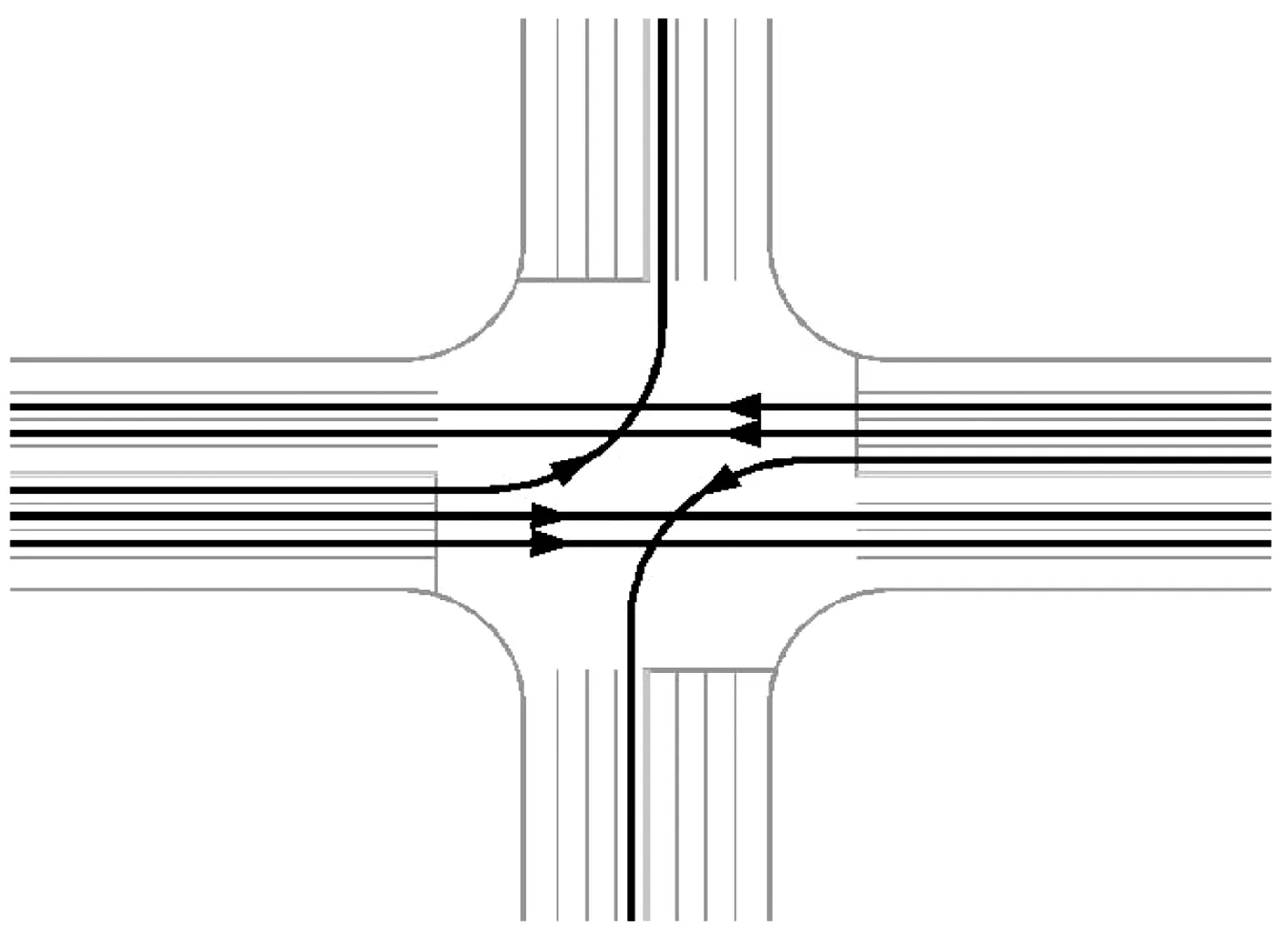
图5 D类合放交叉口车道布局Fig.5 Lane layout of class D mixed release intersection

(11)

2.3.5 一左转穿行三直行(E类)

该类合放车流满足一左转穿行三直行的合放情况，直行交通量较大且连续性强，而左转交通量较小，对于左转车辆需要连续穿行三股直行车道才能通过交叉口，其受直行车流影响较大，可穿行间隙的机会较小。所以，i进口道的基本通行能力，即3个直行车道的通行能力与左转极限通过值的累加量，具体计算如式(12)。同一相位放行状况与几何布局如图6。

图6 E类合放交叉口车道布局Fig.6 Lane layout of class E mixed release intersection

(12)

2.3.6 两左转穿行一直行(F类)

在左转弯方向车辆较多的情况下，进口道方向设有多条左转弯车道，该类合放车流具备两左转穿行一直行的条件。因为左转弯方向流量大，车流间断性较弱，且直行方向流量小，车流间断性较强，左转弯方向的车辆能够穿越间隙的机会较大，同时加大对直行车辆的干扰。所以，i进口道的基本通行能力为一个直行车道的通行能力与两条左转车道最大通过量的叠加，具体计算如式(13)。同一相位状况与几何布局如图7。

图7 F类合放交叉口车道布局Fig.7 Lane layout of class F mixed release intersection

(13)

2.4 合放交叉口通行能力综合计算模型

不同功能等级和渠化的道路交叉产生的路口，合放于相同信号控制相位的进口车道具有较弱的非对称性，但交叉道路因为时间维度上驶过不同信号控制相位分离，所以产生适度的相对独立性。根据上述6种常见的合放路口通行能力分析方法，将不同渠化的路口进行重组，得到不同形式交叉口的i进口合放通行能力计算通式，如式(14)。重组后，常见渠化类型的交叉口基本通行能力如表2。

(14)

路口总通行能力数值为各进口道的通行能力的叠加值，当路口为两相位时，应测算不同进口道的不同方向通行能力值并累加；当其为3个相位时，某组对称进口道单独成为合放相位，而交叉道路的进口道使用两个相位且实行左转和直行单独放行或一个进口道按顺序放行时，被交道路的各进口道需依据具备信号控制设施路口的通行能力计算模型测算；此外，基于路口冲突点复杂程度、各方向车流比例、车道宽度等指标、行人和非机动车干扰等因素对通行能力的折减。因此，合放交通流下城市道路交叉口通行能力综合计算模型如式(15)：

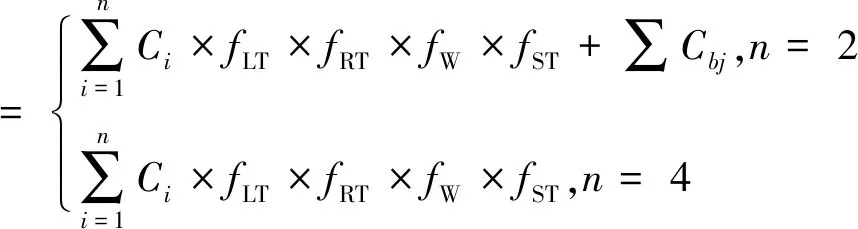
(15)

式中：fLT为左转车辆比例修正系数；fRT为右转车辆比例修正系数；fW为车道宽度修正系数；fST为慢行交通干扰修正系数；∑Cbj为与合放进口方向相交且其不按合放相位控制的道路进口通行能力。

3 模型验证

3.1 实际数据采集与仿真

由于篇幅限制，本研究仅选取济南市新泺大街与颖秀路交叉口为研究对象。该合放交叉口的基本通行能力符合C类和D类通行能力计算方法，与表2中CC+CD的情形相符，同时采集交叉口几何参数、交通运行参数、交通设施、信号控制参数等数据，并利用VISSIM仿真软件将采集数据准确录入，以达到与实际场景相符的仿真效果。

3.2 机动车通行能力模型参数标定

3.2.1 转向比例修正系数

借助VISSIM收集数据，实行控制变量法单独研究左、右转弯的车辆所造成的的干扰，其中在右转比例为10%的条件下，研究其对左转通行能力的影响；在左转比例为10%的条件下，研究其对右转通行能力的影响。

1)左转修正系数

合放交通流中相反方向的直行通行能力受左转弯车流的干扰较大，基本为负相关，具体干扰程度，如图8，左转弯比例修正值如表3。

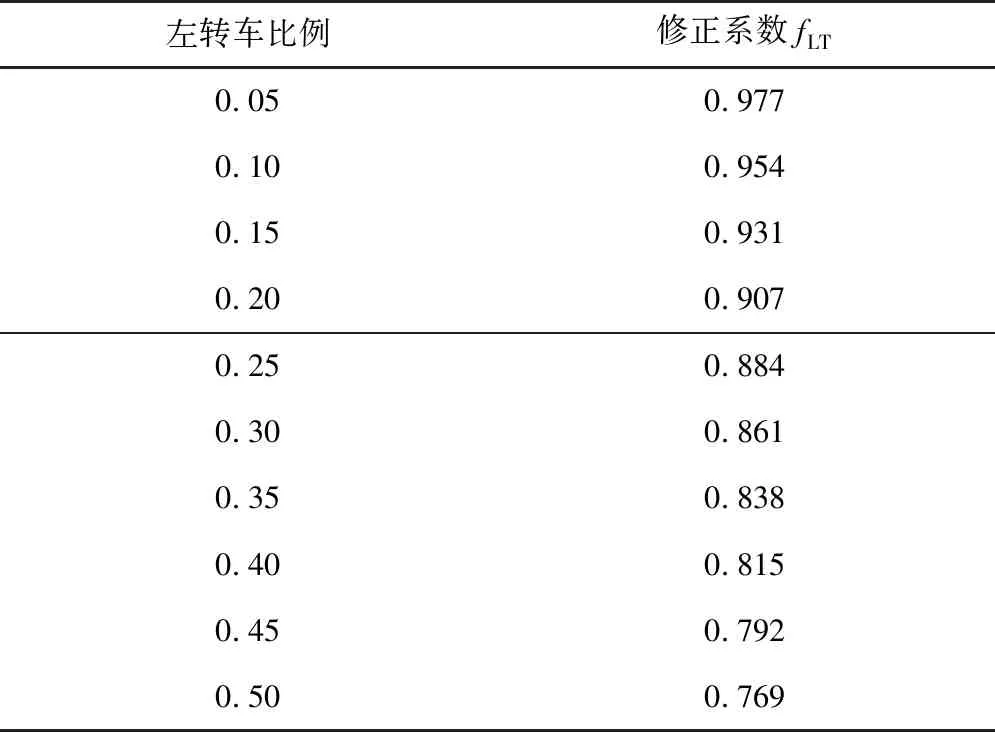
表3 左转车干扰修正系数fLTTable 3 Left turn vehicle interference correction factor fLT

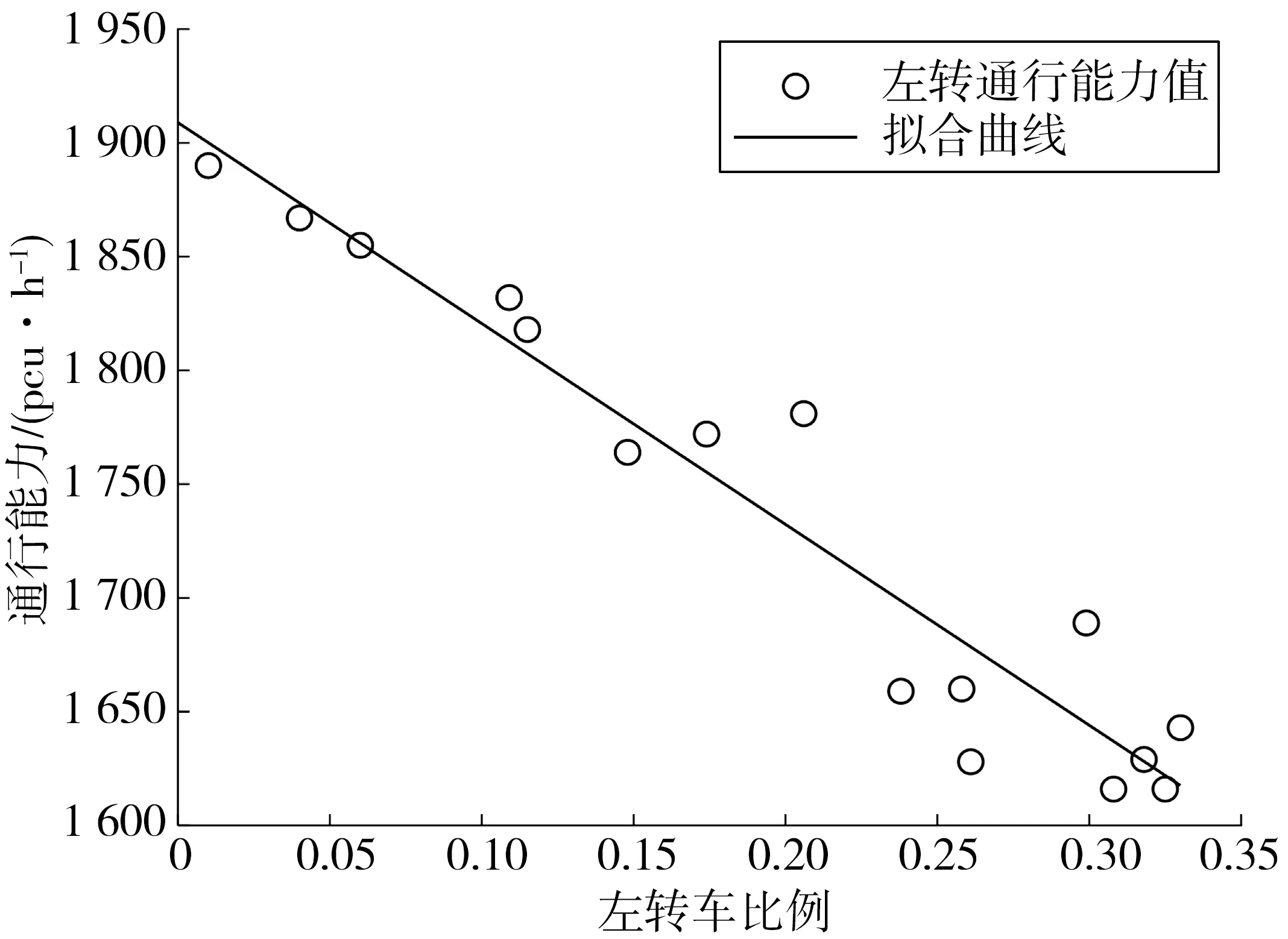
图8 通行能力受左转车比例的干扰Fig.8 The traffic capacity affected by the proportion of left turn vehicles

左转车干扰修正系数fLT为：

fLT=1-0.046 25x

(16)

2)右转修正系数

合放交通流中右转对交叉口通行能力的影响基本为后方车辆受到直行右转车道分流点位置的干扰、其他方向车道通行能力受出口道合流的干扰等方面，其干扰程度与修正值fRT如图9，右转弯转向比例值如表4。

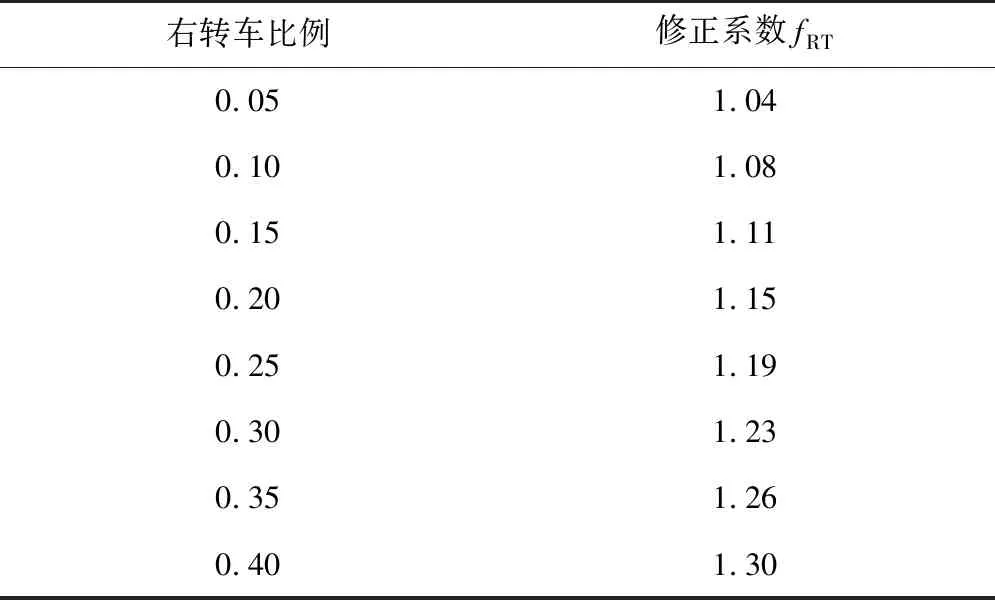
表4 右转弯车辆干扰修正值fRTTable 4 Right turn vehicle interference correction factor fRT

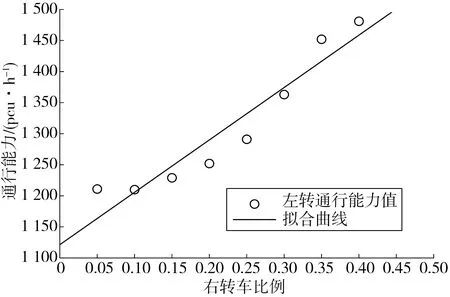
图9 通行能力受右转车比的干扰Fig.9 The traffic capacity affected by the proportion of right turn vehicles

右转车干扰修正系数fRT为：

fRT=1+0.75x

(17)

3.2.2 车道宽度修正系数

统计分析进口道及路段中不同车道宽度与饱和车头时距的关系如图10。

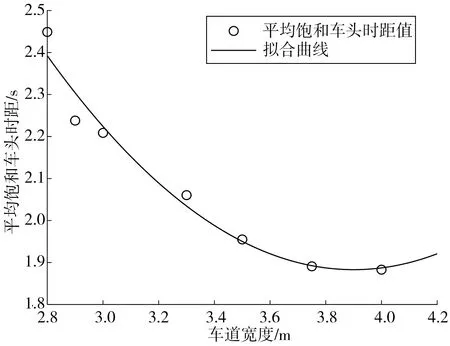
图10 车行道宽度与平均饱和车头时距的关系Fig.10 Relationship between lane width and average saturation headway time distance

按照目前国内外一条车行道饱和车流的规定往往取为1 800 pcu/h，其符合3.5 m宽的标准车道要求，给出各车行道宽度的通行能力及其修正值如表5。

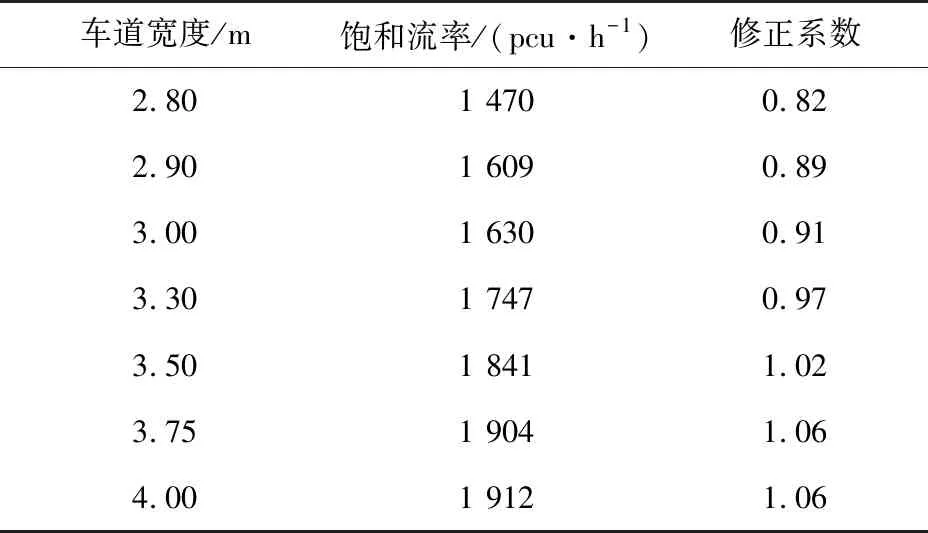
表5 各车行道宽度的通行能力及修正值Table 5 Traffic capacity and correction value of each lane width

由上述测算值的匹配关系，给出车行道宽度修正值与车行道宽度的对应关系如图11。

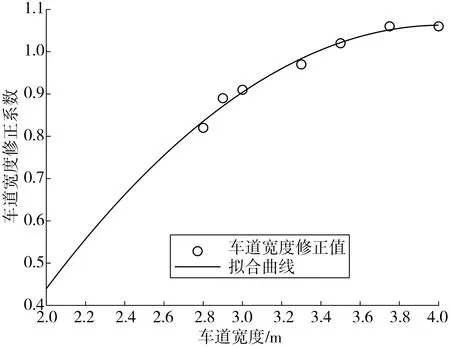
图11 车行道宽度与车行道宽度修正值的关系Fig.11 Relationship between lane width and lane width correction value

fW=-0.15W2+1.24W-1.43

(18)

按照我国交通设计中车道宽度设计规范，相匹配的车行道宽度折减参考数值如表6。

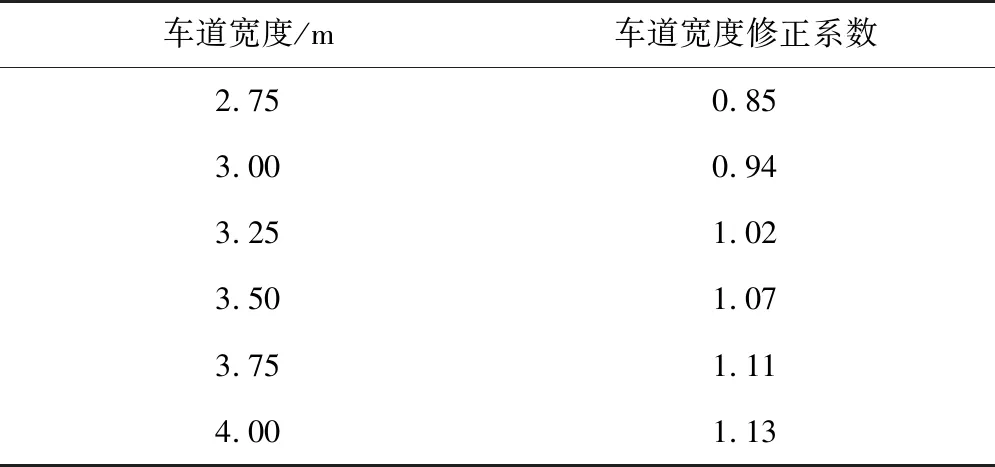
表6 车道宽度折减系数参考值Table 6 Reference value of lane width reduction factor

3.2.3 慢行交通干扰修正系数

合放交叉口的通行能力受行人和非机动车的干扰与非信号控制路口的干扰相近，因此横向修正值参考非信号控制路口的土地性质取值如表7。

表7 慢行交通干扰修正系数Table 7 Slow traffic interference correction factor

3.3 合放交叉口通行能力计算模型验证

根据实际勘测和各方向交通流量统计，计算得到路口右转弯方向，其半径均为20 m，由左转弯方向其车辆运行轨迹，其半径平均为24 m；东侧、西侧、南侧、北侧各进口道左转弯车流量比例各是25.2%、19.5%、22.3%、11.0%，右转弯车流量比例各是10.4%、8.6%、28.0%、7.7%，并选取对应转向比例修正系数。

根据调查数据，计算得出交叉口在调查周期内的实际通行能力，并与合放交通流下的交叉口通行能力综合计算模型获得测算通行能力对比分析如表8。

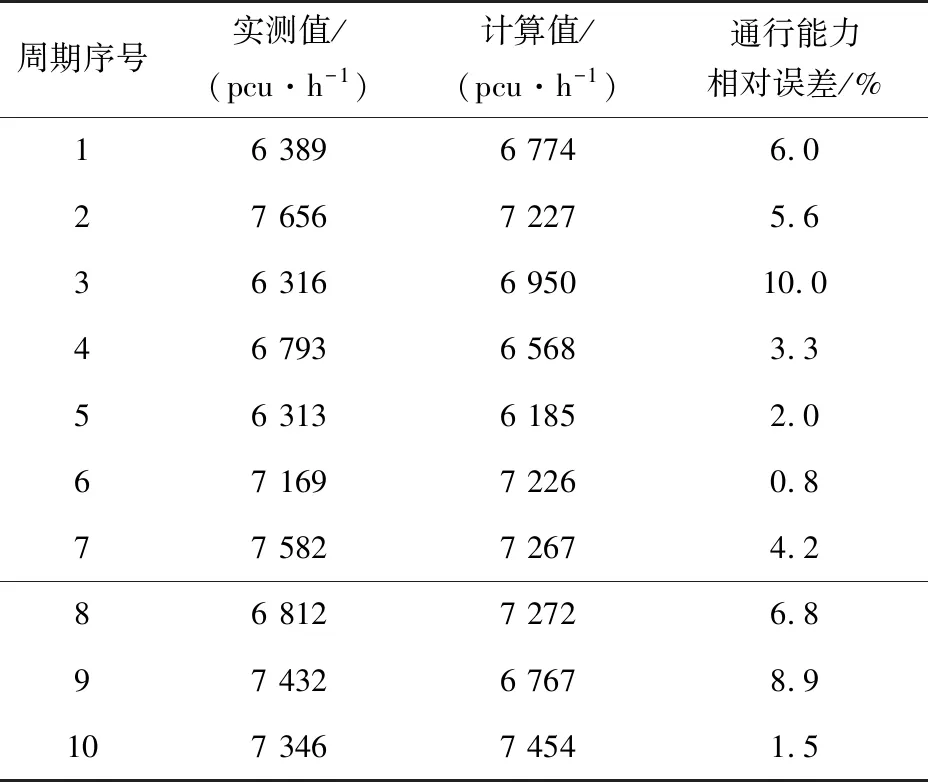
表8 交叉口总通行能力模型计算值与实测值结果对比Table 8 Comparison between calculated and measured results of total traffic capacity model of intersections

由表8可知，该交叉口实际通行能力与测算通行能力基本一致，平均误差为4.9%。因此，笔者建立的合放交通流的交叉口通行能力计算模型能够较好的反映我国城市合放交叉口的实际通行能力。

4 结 论

通过以上研究，得出结论如下：

1)通过对合放交通流的特性分析，提出了交叉口合放是介于信号控制与非信号控制的中间状态，以此在交叉口信控与非信控通行能力计算方法基础上，充分考虑交通冲突复杂系数对直行与右转方向通行能力的折减影响，推导了合放条件下直行、右转交通流通行能力基本计算方法；应用可穿越间隙理论以及提出的左转车辆在相位放行时的前后补偿值，推导了合放条件下左转交通流通行能力基本计算方法。

2)按照合放交叉口进口车道布局划分，对其冲突类比进行划分，并得出了6种合放交叉口进口道的基本通行能力计算模型。

3)应用VISSIM仿真软件对转向比例、车道宽度、慢行交通的影响系数进行修正标定，最终构建了合放交叉口通行能力综合计算模型。实践研究表明，据实际饱和流率数据与测算通行能力数据的对比分析，结果显示二者走向和数目具有同一性，平均误差为4.9%，较好地证明了所建通行能力计算模型的准确性。