集装箱码头场桥调度优化模型研究

郭文文，计明军，祝慧灵，周文杰

(1.上海海洋大学 工程学院，上海 201306;2.大连海事大学 交通运输工程学院，辽宁 大连116026；3.大连海事大学 航运经济与管理学院，辽宁 大连 116026)

0 引 言

集装箱码头是连接不同运输方式的关键节点，其装船效率直接影响着码头的通过能力[1-2]，场桥作为码头物流系统的重要组成部分，其运作效率的高低直接影响着装船作业的运作水平[3]。国内外相关学者以对场桥调度优化问题有不同程度的研究，研究对象主要分为单台场桥和两台场桥。针对单场桥行驶路径优化问题，K.Y.KIM等[4]只考虑一台场桥在同一方向街区内作业路线，建立目标函数为最小化场桥在贝位的启动时间和行驶时间的数学模型；在该研究的基础上，K.H.KIM等[5]、A.H.GHAREHGOZLI等[6]对模型进行改进，建立最小化场桥作业时间的数学模型，并分别利用动态规划和两阶段算法进行求解。然而，上述研究并未考虑集卡对场桥调度的影响，因此，W.C.NG等[7]考虑了集卡到来时刻对场桥调度的影响，研究已知作业任务数量和预期时间下的单场桥作业顺序问题。该类研究成果均将场桥作业任务看做若干子任务，并未对子任务进行划分，为了进一步优化场桥路径；陈雷雷等[8]将场桥作业任务分为阶段任务和阶段内子任务，建立了最小化阶段之间移动距离的基于状态节点网络的路径优化模型，然而模型只考虑了阶段间的距离，忽略了阶段内的场桥移动距离，难以保证求得最优的场桥行驶路线。针对两台场桥行驶路径优化问题，部分学者考虑到集装箱码头的实际操作，研究了两台场桥可跨越作业和同时作业两种方式的调度优化问题；I.F .A.VIS等[9]研究了一个堆场街区内两台可跨越的场桥调度问题；边展等[10]考虑了两台轨道式龙门吊同时作业的约束，研究场桥行驶路径问题。

上述研究成果多在K.Y.KIM等[4]的基础上对算法进行深入的讨论和细化，对数学模型的优化研究较少，且多用启发式算法进行求解，难以求得最优解，笔者在已知岸桥作业子计划和堆场贝位箱量分布的前提下，考虑了单场桥和多场桥的协同作业，区别于现存文献以作业时间为目标建立的数学模型，从场桥移动路径的角度建立了作业贝位数最少及行驶路径最短的两阶段模型，并针对数学模型在AMPL集成开发环境下利用CPLEX求解器求解场桥取箱位置、取箱数量以及取箱路线。两阶段模型能够提高求解效率，且可直接应用于大规模算例的求解，为码头调度人员提供决策支持。

1 问题描述

码头实际装船作业中，往往按照集装箱类型将整个装船任务划分为多个子任务，如表1，每个子任务需求的集装箱为同种类型。规定同一堆场贝位上仅堆存重量、尺寸相同的集装箱，即同一类型的集装箱，如图1。分析可知每个堆场贝位上箱量有限，单个贝位可能无法满足一个子任务要求提取的箱量，即一个子任务需求的集装箱可能堆存在多个贝位内；同时，多个子任务需求的集装箱也可能是相同类型的集装箱。因此，子任务和堆场贝位就出现了多对多的选择，产生多种场桥行驶路径，而场桥数量的不同，也会产生不同的行驶路径，进而影响堆场作业效率。

表1 岸桥作业计划Table 1 Quay crane operation plan

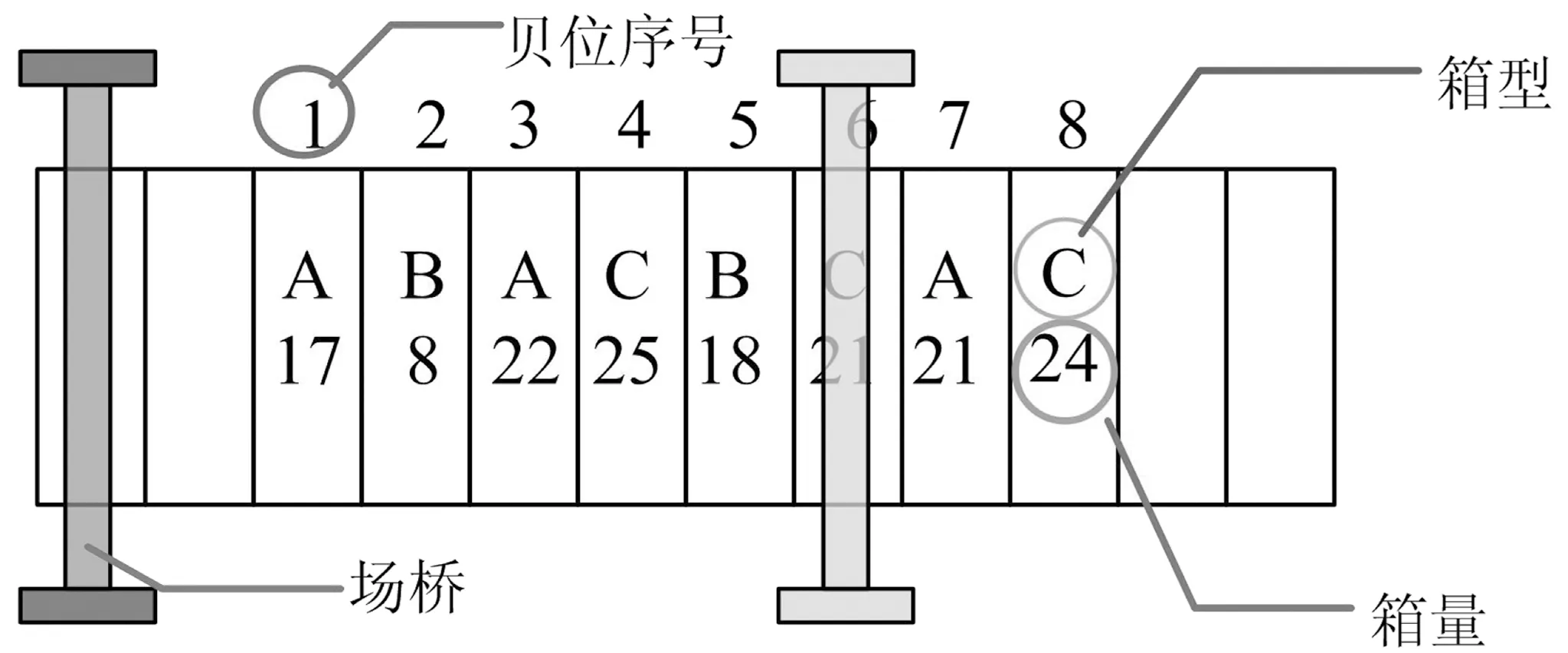
图1 堆场贝位箱量分布Fig.1 Distribution of the number of containers in the storage yard

因此，在已知岸桥作业子计划和堆场贝位箱量分布的前提下，假设岸桥作业子任务要求按顺序依次完成，每个子任务作业的开始必须在前一个子任务完成作业以后，同时堆场贝位要求堆放在同一街区内或在同一直线上，并将贝位依次编号。假设堆场内初始存放的集装箱种类和数量与整个装船任务的集装箱种类与数量完全一致，同种类型的集装箱完全等同，取箱过程中不存在倒箱问题。在此基础上，以场桥总移动距离为目标对码头场桥调度问题进行研究，着重于缩短场桥行驶距离，提高堆场作业效率。

2 数学模型

建立了可直接求解的两阶段数学模型，第1阶段为线性规划模型，确定子任务内场桥需要作业的贝位号及对应贝位内的取箱数量；第2阶段结合第1阶段求得的取箱数量，以总移动距离最短为目标，确定每台场桥作业的贝位号序列和对应贝位内的取箱数量以及场桥行驶路径。

2.1 第1阶段模型

第1阶段在划分子任务的基础上进行研究，主要目的是确定每个子任务内场桥作业的堆场贝位号及对应贝位内的取箱数量。

2.1.1 符号定义

符号定义如下：

i为堆场贝位编号，i=1,2,…,m；m为堆场贝位总数；k为子任务编号，k=1,2,…,n；n为装船任务被划分的子任务总数；g为集装箱类型，g=1,2,…,G，其中1=A，2=B，3=C……依次类推；G为集装箱类型总数；φ(g)为存放g类箱的堆场贝位号集合；ξ(g)为需求g类箱的子任务编号集合；hk为子任务k所需求的集装箱类型；uk为子任务k所需求的集装箱数量；cgi为贝位i中堆存g型箱的初始数量；M为足够大的数值。

2.1.2 决策变量

xik为场桥在子任务k中从贝位i中提取集装箱的数量，为非负整数。

2.1.3 目标函数和约束条件

目标函数为：

(1)

约束条件为：

(2)

(3)

(4)

xik≤M·Xik[k=1,2,…,n，i∈φ(hk)]

(5)

xik≥Xik[k=1,2,…,n,i∈φ(hk)]

(6)

xik≥0 [k=1,2,…,n,i∈φ(hk)]

(7)

Xik∈{0，1}[k=1,2,…,n,i∈φ(hk)]

(8)

其中，式(1)为提取所有子任务需求的集装箱后场桥作业过的堆场贝位数最小；式(2)为每个子任务都能完成所需求的箱量；式(3)为堆场贝位内集装箱的初始存储量与所有子任务需求的箱量一致；式(4)为所有子任务在某一贝位的提箱量之和等于该贝位堆存的集装箱；式(5)和式(6)为xik和Xik的关系，当xik为正整数时，Xik为1，当xik为0时，Xik为0；式(7)为决策变量是非负整数，当场桥在子任务k中从贝位i中提取集装箱时，xik为正整数，否则为0；式(8)为Xik是0～1变量。

第1阶段模型的求解结果是满足约束条件的xik解中非零数最少、零值最多的解，也就是场桥完成装船子任务作业的堆场贝位数最少的解，用矩阵Aik表示上述解，定义其对应的0～1矩阵为Bik，根据性质一，分析可知上述解集中肯定存在满足场桥行驶总路径最短的解。

2.1.4 性质一

矩阵Aik中所有的元素中，如果元素零越多则非零元素越少，当元素零的个数最多时，所有非零元素所在行的差值之和不大于其他时候的和，即当元素零最多时，解中一定存在使将所有非零元素所在的行按列随机排列后相邻差值之和最小的情况。

2.2 第2阶段模型

2.2.1 符号定义

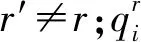
2.2.2 决策变量

2.2.3 目标函数和约束条件

目标函数为：

(9)

约束条件为：

(10)

(11)

(i∈φk，k=1,2,…,n,r=1,2,…,R)

(12)

(13)

(14)

(k=1,2,…,n,r=1,2,r′,…,R)

评析 例3的解答，让学生回忆平移的性质：平移中对应点之间的连线平行且相等，图形左右平移中对应点的纵坐标的不变性；例4的解答，让学生把握解平移问题的一条主线——对应点的连线平行且相等，对应边平行且相等，由此得平行四边形；例5的解答，从“没有现成点”到找点，再找其对应点，让学生学会了联想和转化；例6的第一问，需确定相似三角形求OE，第二问需根据平移中对应点之间平移的方向和距离的相同性构造全等三角形，将两条变量线段A′B、BE′转换化成有公共动点A′的线段，将两条变量线段的和的最小值问题转化为“两点之间，线段最短”的问题.

(15)

k=1,2,…,n,r=1,2,…,R)

(16)

k=1,2,…,n,r=1,2,…,R)

(17)

其中，式(9)为最小化场桥完成子任务的移动距离；式(10)和式(11)为场桥从o点开始到d点结束；式(12)为作业的堆场贝位的流入量和流出量必须相等；式(13)为每个子任务中避免形成回路，|φk|为集合φk的元素个数；式(14)为场桥进行作业时必须完成一个子任务才能进行下一个子任务工作；式(15)为场桥作业的安全距离且避免跨越作业；式(16)和式(17)为决策变量为0～1变量。

3 模型验证

在AMPL集成开发环境下调用CPLEX求解器对模型直接求解，Intel(R) Xeon(R) CPU E5- 1603v3 2.8 GHz及8G内存平台下测得两阶段模型的最优解，验证模型的准确性。以表1和图2的具体算例为例，集装箱船总装箱量为156 TEU，其中，A型箱60 TEU，B型箱26 TEU，C型箱70 TEU。利用CPLEX求解器对第1阶段模型进行求解，计算得出满足约束条件的xik的集合Aik及其对应的0～1矩阵Bik，结果为：

第1阶段目标值Z=10，即场桥作业的最少贝位数为10，CPU运行时间t1=0.05 s，每个子任务的作业贝位为矩阵Bik非零元素所在的行，对应贝位的取箱数量为矩阵Aik中的非零元素。

在此基础上，根据建立的第2阶段模型，当场桥数量r=1，即单场桥作业时，场桥最优行驶路径如图2，场桥作业顺序及对应贝位内取箱数量如表2，最短移动距离S=17 m，CPU运行时间t2=0.04 s，两阶段的总运行时间为t=0.09 s。

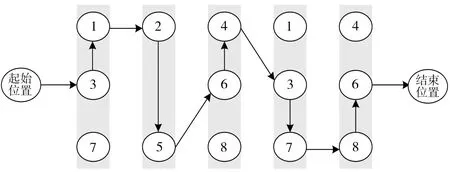
图2 单场桥作业行驶路径Fig.2 Travel route for single yard crane

表2 单场桥作业下贝位的取箱数量Table 2 Number of containers taken from the bay under single yard crane operation

当场桥数量r=2，即双场桥作业时，场桥的最优行驶路径如图3，场桥作业顺序及贝位取箱数量如表3，最短移动距离为S=12 m，CPU运行时间t2=0.05 s，两阶段的总运行时间为t=0.1 s。

图3 双场桥作业行驶路径Fig.3 Travel route for double yard crane

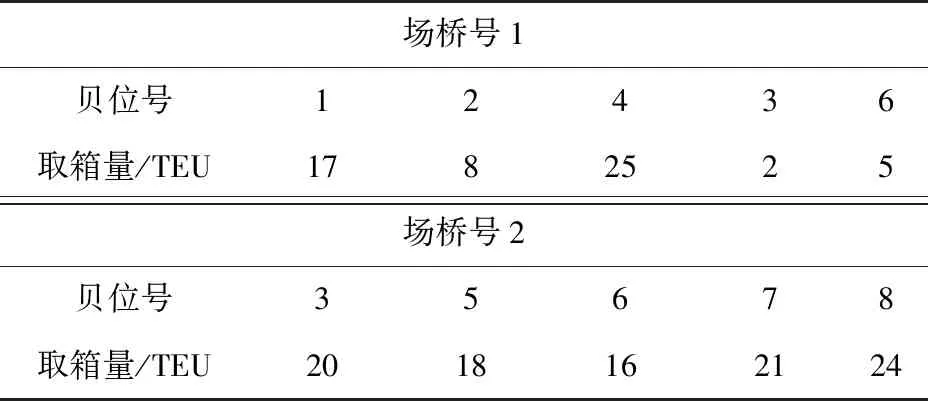
表3 双场桥作业下贝位的取箱数量Table 3 Number of containers taken from the bay under double yard crane operation

由上述算例可知，笔者建立的数学模型可直接进行求解，且运算时间较短。同时，上述算例的求解及计算结果验证了数学模型的准确性，且采用双场桥比单场桥行驶距离更短，为码头堆场资源调度提供决策支持。

4 数值试验

4.1 算例分析

运用两阶段模型对以下8组算例进行求解，表4和表5分别为单场桥与双场桥作业时，堆场作业的贝位数及场桥移动距离。

由表4、表5和图4可知，在第1阶段求得的作业贝位及取箱数量下，第2阶段采用单场桥或双场桥确定作业路线时，场桥总行驶距离相差不大，也就是说场桥行驶距离与其数量没有密切的关系。堆场为节省场桥作业成本，可选择单场桥进行堆场作业，但随着提取箱量的增加，单场桥作业并不能满足装船时间的要求，而采用双场桥在提高作业效率的同时也会增加一定的作业成本。因此，如果装船作业时间较短，码头更注重于作业效率，可采用双场桥，否则可采用单场桥。利用CPLEX对模型进行求解，可以较快地得到最优结果，运行时间较短，证明了模型的准确性和高效性。

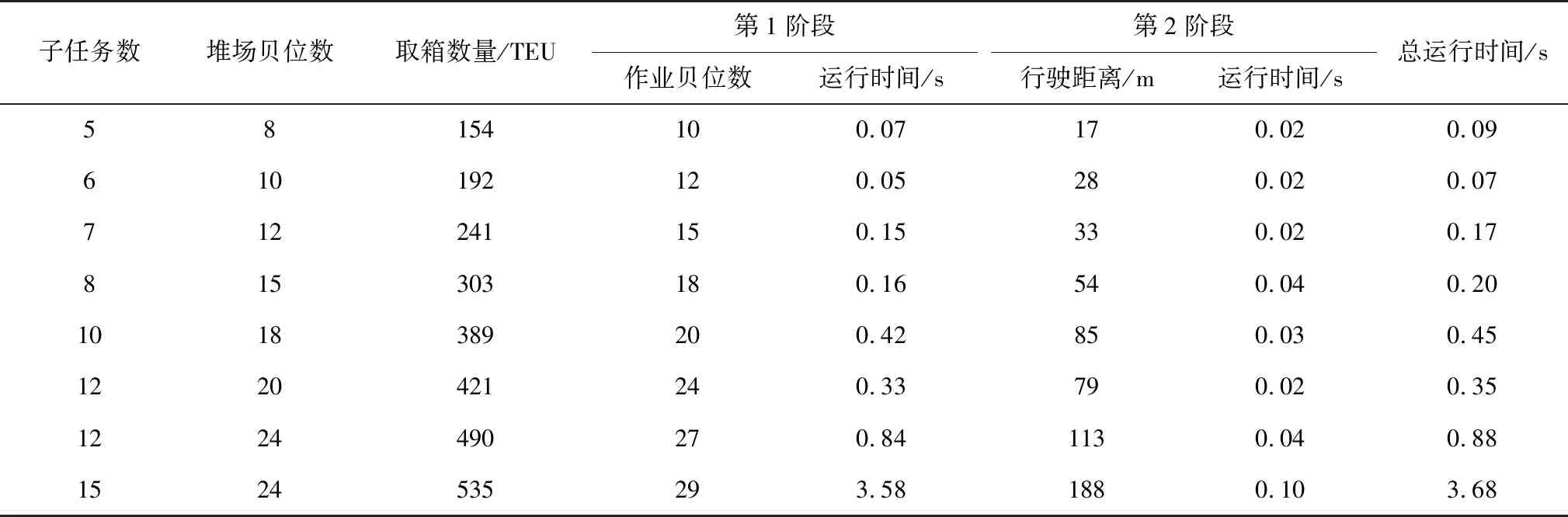
表4 单场桥作业贝位数及距离Table 4 Number of operation bays and travel distance for single yard crane

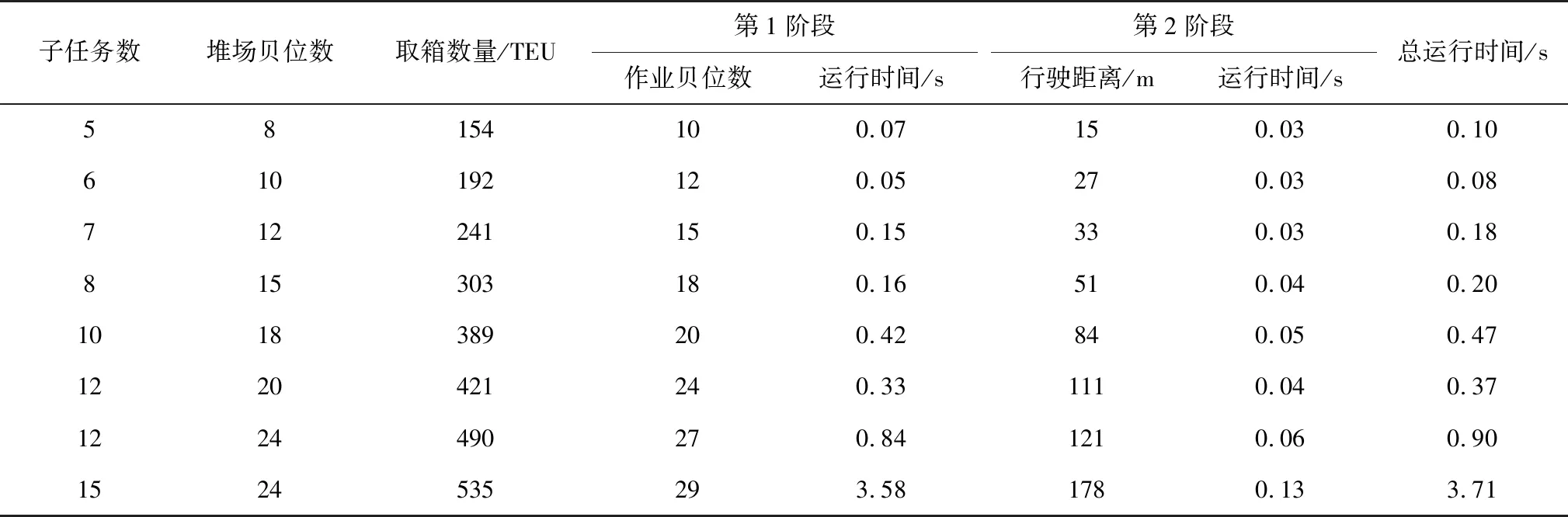
表5 双场桥作业贝位数及距离Table 5 Number of operation bays and travel distance for double yard crane

图4 不同取箱数量行驶距离比较Fig.4 Comparison of driving distance for different numbers of containers taken out

4.2 算法比较

为进一步验证算法的优越性，将建立的两阶段模型直接求解与文献[8]中的顺序作业法、贪婪作业法、基于整数编码的遗传算法进行比较，验证了两阶段模型的有效性，表6和表7为文献中的算例。

表6 岸桥作业计划Table 6 Quay crane operation plan

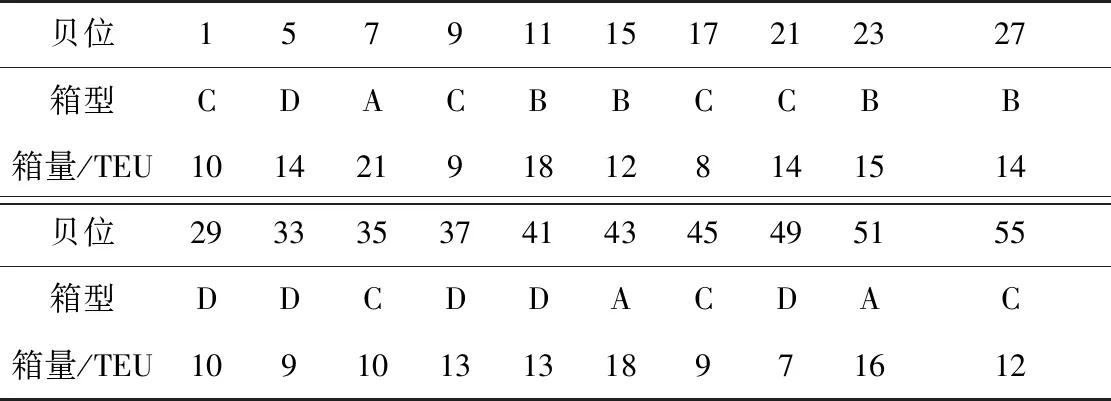
表7 堆场箱量堆存状态Table 7 Yard bays stacking status

根据文中建立的模型，采用单场桥作业，利用两阶段模型进行求解的结果为Z=22，S=266，两阶段的总运行时间为t=0.4。由此可知文中的两阶段模型场桥总移动贝位数为266，作业路径如图5，与文献[8]中算法进行比较，结果如表8。

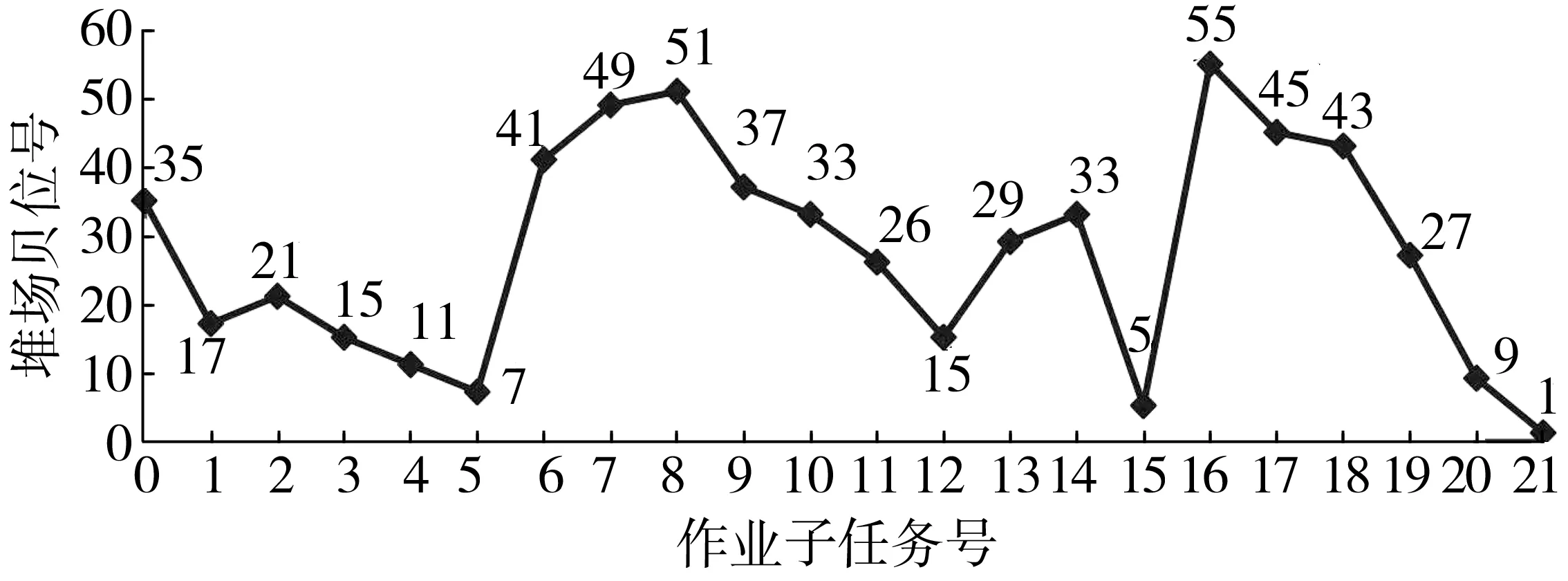
图5 两阶段模型作业路径Fig.5 Travel route of two-stage model

表8 算法比较Table 8 Algorithm comparison

表8中模型的改进程度为两阶段数学模型与顺序作业法、贪婪作业法及遗传算法相比的改进程度，负号表示两阶段模型的移动总贝位数小于其它算法下的移动总贝位数。由表8可知两阶段模型与顺序作业法下的移动总贝位数887相比，总移动距离缩短了70.0%，与贪婪作业法下的643相比，总移动距离缩短了58.6%，与遗传算法下的595相比，总移动距离缩短了55.3%。因此，建立的两阶段模型能够明显的缩短场桥移动距离。

为进一步验证模型的普遍性，利用文献[8]中的顺序作业法与贪婪作业法对上述算例求解，且与两阶段模型进行对比，具体结果如表9。

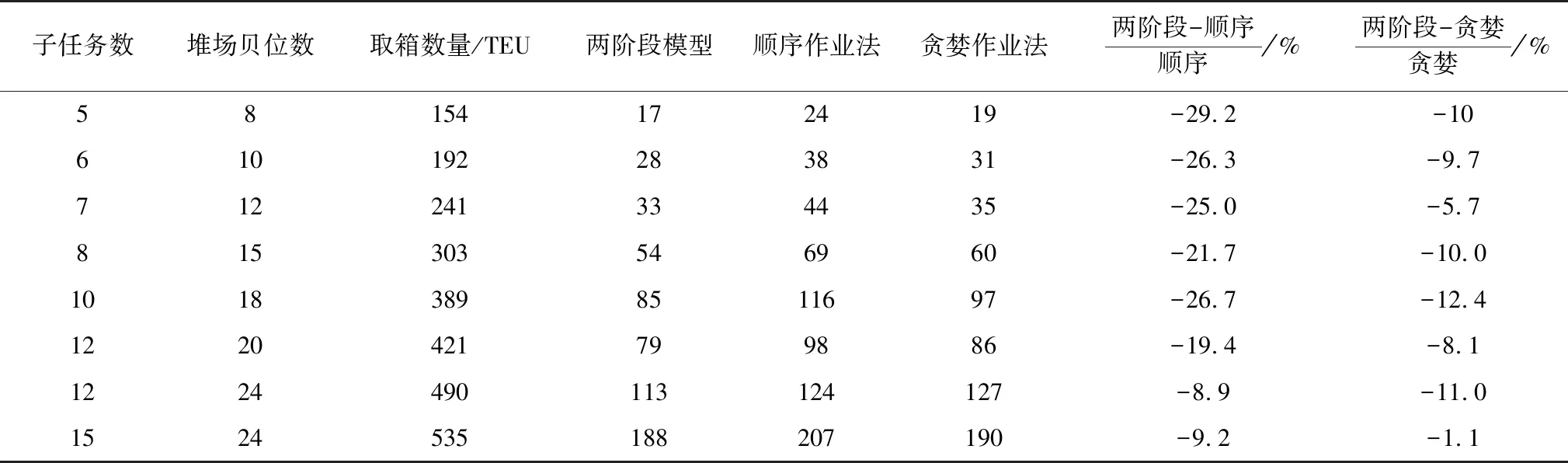
表9 单场桥下算例比较Table 9 Comparison of examples for single yard crane

表9中负号表示两阶段模型下场桥行驶的总距离要小于顺序作业法及贪婪作业法下的行驶距离，数值大小表示两阶段模型下行驶总距离的减少程度。结果表明，建立的两阶段模型可以较快地得到最优解，在单场桥作业的情况下，与顺序作业法相比，行驶距离缩短10%～30%，与贪婪作业法相比，行驶距离缩短10%左右，表明笔者建立的模型具有更显著的应用价值和研究意义。

5 结 语

在已知岸桥作业任务及堆场贝位箱量分布的条件下研究集装箱码头场桥调度优化问题，与现有数学模型对比，建立了场桥作业贝位数最少及行驶距离最短的两阶段场桥移动路径模型，将问题进行简单化、分步化，运用两阶段模型对场桥取箱位置、取箱数量以及取箱路线进行求解，得到场桥在每个任务中作业的堆场贝位的顺序及对应贝位内的提箱数量，使得场桥行驶距离最短。与现有文献比较，两阶段模型比顺序作业法缩短10%～30%的行驶距离，比贪婪作业法缩短10%左右的行驶距离，且优于文献中的遗传算法，验证了模型的准确性和有效性。为码头工作人员提供了决策支持，有利于提高集装箱码头的运营效率。