路网抗震可靠性及震后运输调度路径选择研究

2021-06-21张重阳黄淑萍

重庆交通大学学报(自然科学版) 2021年6期

张重阳,黄淑萍

(上海交通大学船舶海洋与建筑工程学院，上海 200240)

0 引言

近年来我国地震灾害预报水平不断提高，但由于地震发生机理的缘故，目前仅能做到对已发生地震的预警而不能做到对未来地震的预测。近十年在全球范围内发生的地震灾害具有这些相似的特征：道路交通网络受到损坏，以至于到达受灾点的路径被斩断，给震后应急救援工作带来巨大困难，救灾物资和人员无法及时到达救援一线，造成受伤死亡人数增加，灾情严重，带来巨大的经济和社会损失。道路网络作为抗震救灾的第一生命线，不仅是救援物资运输的首要渠道，也是影响灾后人员疏散，消防人员、救援部队以及道路修复工程队进行救援的关键因素。因此，对路网抗震可靠性及震后运输调度路径优化研究并做出科学的选择，可以提高调度效率，最大化地降低损失和伤亡率，对维护灾后秩序有着极其重要的现实意义。

在路网抗震可靠性的研究中，国内外一些学者先后研究了震后道路交通网络的连通性，并对其进行了模拟实验，提出震后路段通行概率的计算公式，建立用蒙特卡罗模拟方法分析路网连通性的仿真模型，对路段单元和路网节点进行可靠性评价研究，并对在投资约束条件下使交通系统可靠度最大的加固路线优化设计的数学模型进行研究[1-3]。尹红英等[4]提出了依据贝叶斯网络的推理方法来量化分析交通道路网络中各个路段失效对路网的整体影响的方法，并将其应用于路网脆弱性的概率表现研究中，但文中建模的前提是做出假设，设定每个路段的先验失效概率与路段长度成正比，这并不符合路网的实际情况。笔者在构建评估路网抗震可靠性的贝叶斯网络时参考这一研究方法，不同的是对路网的扰动因素是地震作用，且路段的先验连通概率通过计算得出，更具说服力。

目前针对震后应急救援运输调度问题的研究中，大部分研究以运输时间最短、运输路径最短、调度车辆最少、供给点搭建成本最小为目标来进行分析和决策。陈杰[5]对应急物资运输调配数学规划模型的遗传算法、灾害时应急救援物资车辆运输线路的选择问题模型及优化算法进行了相应的研究；王挺等[6]将震后道路的车辆通行时间和道路安全风险性考虑在内，设计了运输车辆数量少于配送点数的多目标配送路径优化模型；在已有研究的基础上，沈明望等[7]在研究震后救援物资运输的路线选择时，将该问题看作是多属性决策问题。运用了旅行商理论对运输时间性、费用性和风险性这3个不同决策属性进行分析，构造相应的目标函数，把多属性决策问题变为单一决策目标问题，证明多属性决策理论可用于震后运输调度路径选择中。但文章中给出的属性较为模糊，且未对该问题进行定量分析。因此，在已有研究的基础上，将震后运输调度问题视作单一供给点向多目标配送问题，同时将多属性决策理论应用于震后运输调度路线选择中，进一步确定了决策问题中各个属性的含义，并对其进行定量分析。

路网的抗震可靠性是路网在地震作用下保持其连通功能的能力，用震后路网的连通概率来定量表达。笔者通过每个路段单元的连通概率得到结构受损结果，作为贝叶斯网络模型的先验概率，再利用贝叶斯网络建立路段间的相互作用关系，从而得到路网整体的抗震可靠性，作为评估路网功能受损的依据，这样就将结构受损和功能受损两部分结合在一起。并以此作为震后运输调度路径选择的依据之一。在研究震后运输调度路径选择时，笔者采用多属性决策理论，以运输时间、运输距离和路径可靠性为决策属性，构建决策效用函数模型并对该模型进行求解分析，做出最优路径选择。

1 路网抗震可靠性分析

对于一个交通系统来说，每个构成系统单元的性质都对系统整体的性质产生影响。所以对于一个路网，每个组成单元(如路段、桥梁等)的可靠性直接影响了路网整体的可靠性。

1.1 路段抗震可靠性影响因素

学界中一般将结构可靠度定义为结构完成预定功能的概率，笔者将路段的抗震可靠度定义为在发生地震灾害的情况下，路段保持连通的概率。影响路网抗震可靠性的主要因素[8]有：路段损坏、桥梁损坏、沿街建筑物倒塌[9]及震后人车干扰。笔者把路网中各个路段的自身损坏和桥梁损坏作为主要研究对象，其中路段单元定义为路网模型中任意两个相邻节点之间的一条直道路，具体在文中应用的物理网络中表现为两个相邻乡镇之间的一条直道路。同一对节点间方向发生变化的道路视作不同路段。

1.1.1 路段抗震可靠性分析

对于路段抗震可靠性，分析时需要考虑的因素有许多，在这种影响因素多、综合分析处理信息较为困难的情况下可采用模糊综合评价方法。在模糊综合评价方法体系中，采用平均震害度来表示单个路段的受灾程度。对历史地震灾害数据中归纳总结，确定了7个震害因素：道路受震烈度、路基土类别、场地类型、地基失效程度、路基类型、路基高度差、路段设防烈度。模糊综合评价方法采用基于概率的性能评估，每个单独的震害因素的不同对应类别对整体平均震害度的量化影响不同，路段平均震害度可由式(1)[10]计算，震后路段连通概率由式(2)计算。其中式(1)是为方便计算，从而设震害度曲线为正态分布条件下的表达式。式(2)根据道路破坏等级与震害度之间的关系得出[11]：

(1)

Pr=1-Dr

(2)

式中：Dr为路段的震害度；Xj为路段的震害因素对应的量化值如表1，各个震害因子对应的量化值均通过对以往震害经验总结得出；Pr为震后路段连通概率。

表1 路段震害因子量化值[11]Table 1 Quantified value of seismic damage factor of road section

1.1.2 桥梁抗震可靠性分析

地震发生后，桥梁是路网中可靠性较低的部分，它的损坏对路网有着极大的影响[12]。目前地震工程学界常采用基于非线性静力分析的pushover或历史震害记录统计来评估桥梁在地震发生后的连通概率。前者需要桥梁的具体设计参数，以及建立大量非线性模型和庞大算力。后者基于历史数据和资料信息，对大量地震后灾害情况做出回归统计分析，从而建立出桥梁的震害经验预测公式。笔者采用朱美珍[13]提出的非线性桥梁震害预测经验公式来计算桥梁的震害度，具体计算公式为：

(3)

式中：Db为桥梁震害度；w0为修正系数，建议取值为0.85；wij为第i项中j因素的统计加权系数如表2，δij为预测桥梁的观察数值，取0或1。

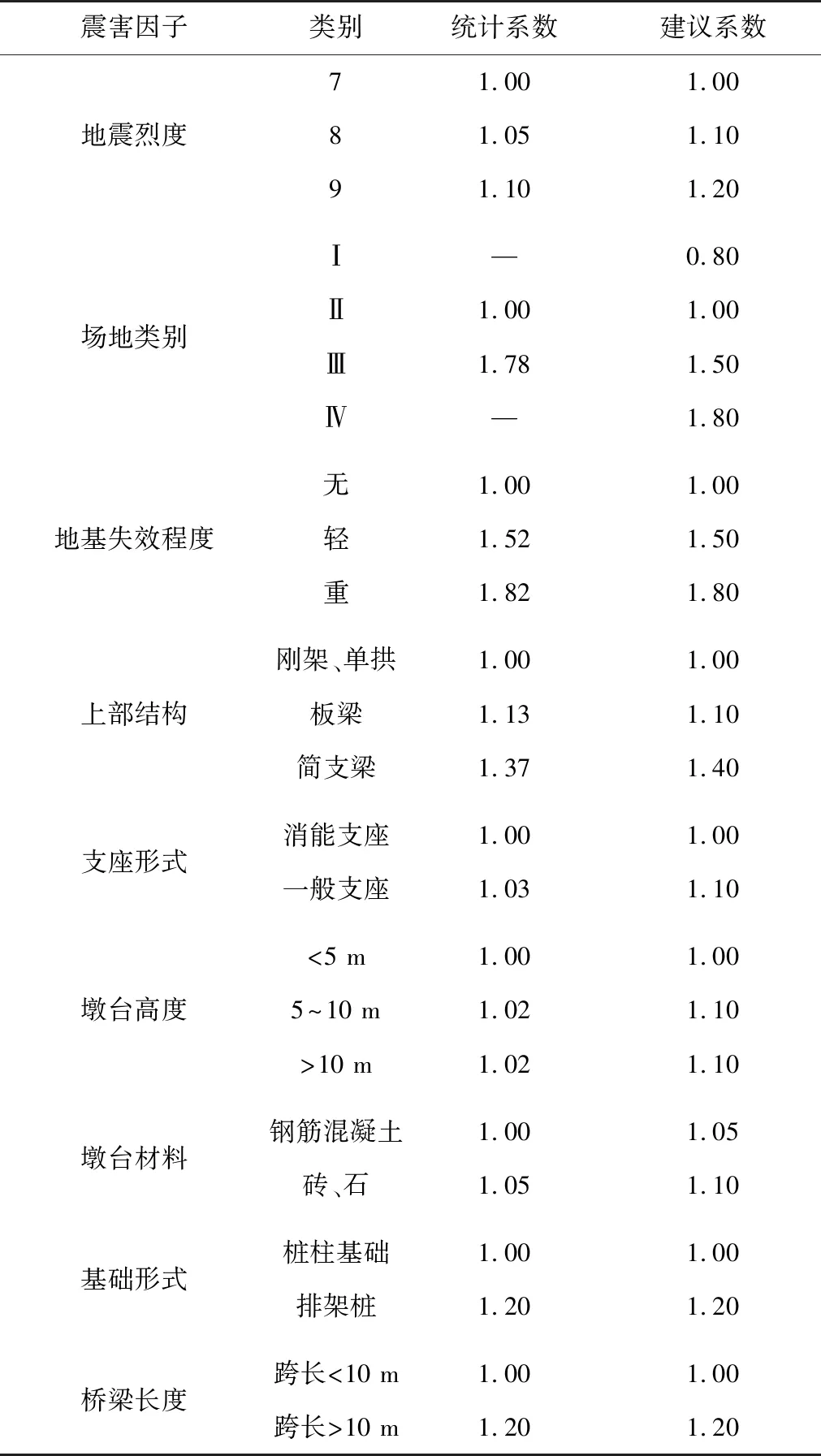
表2 桥梁震害因素影响系数预测建议值[13]Table 2 Recommended prediction value of influence coefficient of bridge seismic damage factors

一般而言，桥梁的震害等级分为：基本完好、轻微破坏、中等破坏、严重破坏和毁坏5个等级[14]。朱美珍对震害资料较全的100座公路桥梁进行总结后，通过对它们绘制预测震害指数频次累积分布曲线，得到了桥梁5个震害等级的临界震害指数。由式(3)计算所得的桥梁震害度Db结合表3，对桥梁震害程度进行等级划分，分为基本完好、轻微破坏、中等破坏、严重破坏和毁坏5个等级，不同等级的震害度范围如表3。在此基础上可以预测桥梁震后的连通概率Pb，即桥梁抗震可靠度。

表3 桥梁震害度与连通概率[13]Table 3 Seismic coverage and connection probability of bridge

对于包含桥梁的路段，将其看作路段单元与桥梁单元串联而成的结构，任一单元损坏时，整个路段就损坏。所以，这种路段的通行概率为该路段本身的连通概率与其中桥梁连通概率之积：

P=Pr×Pb

(4)

1.2 路网结构模型

路网结构模型可通过图论进一步简化和阐释。路网中不同的供给点或者需求点，可以视为图论中图的节点，连接路网中供给点和需求点之间的路段，可视为图论中图的弧。路网结构中路段与路段之间的连接，可以简化总结为串联、并联和混联。

对于串联系统而言，只要其中一个单元失去效用，则整个串联系统发生故障，用Ri(t)表示单元i的可靠度，则根据串联系统特性可知系统可靠度Rs(t)为：

(5)

对于并联系统而言，系统中只要还有一个单元可以运行，则整个系统都可以正常运作。只有当所有元件都出现故障时，并联系统才会失效。根据并联系统特性可知并联系统的可靠度计算方法为：

(6)

对于一个路网系统，只要系统中仍有一条路径保持连通，则该系统便保持其效用。因此，路网可以视作由不同路径以并联的方式组成的。而对于一条路径，只要构成该路径中的任一路段失效，则整个路径便不再连通。因此，路径可以视作由不同路段以串联方式构成的。

1.3 贝叶斯网络模型

1.3.1 贝叶斯公式

在贝叶斯网络模型中，节点表示不同的变量，箭头连接两个具有因果或是依赖关系的节点。且贝叶斯网络是基于概率公式推理的，贝叶斯推理的基本公式为:

P(D|H)/P(D)=P(H|D)/P(H)

(7)

式中：P(H|D)为后验概率；P(H)为先验概率，即事件H的发生概率；P(D|H)为似然率，用于刻画产生数据的过程或机理；P(D)为无条件概率，起归一化常数的作用。

1.3.2 贝叶斯网络的构建

在构建贝叶斯网络时，首先要确定网络中的节点含义。笔者主要研究震后供给点与需求点之间路网的连通概率。因此，将路网中的路段、路径和供需点构成的OD对确定为网络中的3层节点，其中路段为顶层节点，OD对为底层节点。

在确定网络节点后，需建立节点之间的关系，从而构成贝叶斯网络模型。笔者在确定好节点后，依据路段串联构成路径以及路径并联构成路网的结构特征建立节点之间的相互关系。对于一条路径而言，只要构成该路径的任一路段失效，则该路径就不再连通。对于一个OD对而言，该OD对之间的所有路径共同并联构成了该OD对，只要仍有一条路径保持连通，则该路网便没有失效。根据节点间关系，结合式(5)和式(6)，可以在构建贝叶斯网络的软件中输入节点的概率分布表，从而完成评估路网抗震可靠性的贝叶斯网络的构建。

为了进行贝叶斯网络推理，还需要确定事件的先验概率分布表(CPT)。根据1.1中阐述的方法计算路段抗震可靠度，将其作为顶层节点的概率分布，即震后路段连通的先验概率分布。

在此基础上，结合构建的贝叶斯网络模型，通过计算可以得到各路径与OD对的连通先验概率。将OD对保持连通作为发生事件，利用贝叶斯公式加以计算，可以得到在OD对保持连通的条件下，各个路径与路段的连通后验概率。

2 震后运输调度路径选择

2.1 问题分析

震后运输调度问题是一个综合性较强的研究，其中包括运输车辆安排、运输路径选择、供给点选址及搭建等问题。笔者选取的研究方向为震后运输调度的路径选择问题。

由于地震发生后，受灾地区道路连通情况会受到不同程度的影响，在解决该问题时需在OD对之间保持连通的条件下进行路径选择。因此，笔者将根据贝叶斯网络模型求得连通后验概率，来定量描述路径的抗震可靠性。在此基础上，结合多属性决策理论，构建针对震后运输调度路径选择的决策效用函数模型。该模型中定量研究的3个决策属性分别为运输距离、运输时间及路径可靠性。其中运输距离为路网中不同路径的客观长度；运输时间则利用BRP函数来定量分析；路径的可靠性用其抗震可靠度来定量描述，即路径的震后连通概率。

2.2 模型构建

2.2.1 属性标准化处理

一般来说，属性分类有成本型、效益型和区间型3类。成本型也称作负属性，该类属性值越小，对问题的隶属度就越高，效果越好；效益型也称作正属性，该类属性值越大，对问题的隶属度就越高，效果越好；而区间型属性又叫适度型属性，该类属性值越接近某个常数，对问题的隶属度越高，效果越好。

对于不同的属性，它们本身具有不同的度量方法，单位、量纲、数量级等标准都不同，在进行多属性决策时无法直接对各个初始属性进行分析和评价。因此，在确定影响研究问题的3个属性后，需对其进行标准化处理。选用的标准化处理方法为极差变换法，具体计算方法为：

(8)

式中：yi为标准化属性值；xi为初始属性值；xmin和xmax分别为该属性的最差值和最优值。

研究的3个决策属性中，运输距离和运输时间均为成本型属性，即属性值越低，效果越优；路径可靠度属于效益型属性，即属性值越高，效果越优。则根据式(8)可以得到3个决策属性的标准化处理结果为：

(9)

(10)

(11)

式中：yDi为某一OD对之间第i条路线的运输距离标准化属性值，第i条路线的运输距离为Di；YTi为某一OD对之间第i条路线的运输时间标准化属性值，Ti为第i条路线的运输时间；设yPi为某一OD对之间第i条路线的可靠度标准化属性值，Pi为第i条路线的震后可靠度，此时可靠度的值应为在发生地震后，保证该OD对连通的基础上，第i条路线的可靠度，即该路线连通的后验概率。

在计算震后运输时间时，应当把震后道路受阻情况考虑在内，故根据美联邦公路局总结的BRP函数来计算震后运输时间，如式(12)：

(12)

式中：ta为路段a的实际行程时间；ta0为路段a的自由行程时间；fa为路段a的交通量；Ga为路段a的通行能力，由于参与震后运输调度多为中型货车或医疗车，故而笔者将路段通行能力用震后路段的连通概率与中型车当量通行能力的乘积表达；α,β为常数，通常取α=0.15，β=0.40。

2.2.2 决策效用函数构建

在确定了运输距离、路线可靠度、运输时间3个属性的标准化计算方法后，仍需要确定3个属性在决策中所占的权重。在权重信息不足的情况下可根据经验信息及已有证据进行推理[15]，根据各个属性在决策问题中的重要程度设定各属性权重。以保障灾后运输调度安全和高效为目的，路径可靠性和运输时间更为重要，因此在权重设定时高于运输距离属性，具体权重值在后文实例分析中给出。设γD,γP,γT分别表示运输距离、路线可靠度和运输时间在决策中所占权重，权重向量γ=(γD,γP,γT)T，满足γD+γP+γT=1。则对于路线i的整体决策效用函数模型为：

Yi=γDyDi+γPyPi+γTyTi

(13)

根据该决策效用函数模型，同一OD对之间的多条路径在选择时，将对应路径的整体决策效用函数值作为选用优化路径的依据，决策效用函数值最高的路径即为最优路径。研究单一供给点对多个需求点提供震后应急救援的运输调度，在得到所有OD对的路径选择后可以分析不同路段在震后应急救援中所承担的运输调度任务轻重，为震后救援决策提供理论依据。

3 实例分析

以宿迁市宿城区东部6个镇之间的路网作为研究对象，运用前文所述理论方法进行实例分析。

3.1 路网基本信息

所选路网共包含12条路段、3个桥梁。应急服务点(应急物资中转站)设在洋河镇(A点)，应急需求点为郑楼镇(B点)、仓集镇(C点)、中扬镇(D点)、屠园乡(E点)、陈集镇(F点)5个镇。将路网按1至12编号，桥梁为b1、b2、b3，标记后如图1。

图1 宿城区部分路网Fig.1 Part of Sucheng district road network

其中，路段9为双向两车道的二级公路，其他路段均为三级或四级公路。地震参数选用我国东南地区地震烈度衰减模型参数[16]，所选路网位于郯庐地震带末端，依照第四代地震烈度区划图设定地震为7.5级，震中位于33.9 304°N，118.32 250°E，震源深度为10 km，破裂方向为80°。具体路段长度、设计时速、通行能力及受到的地震烈度如表4。

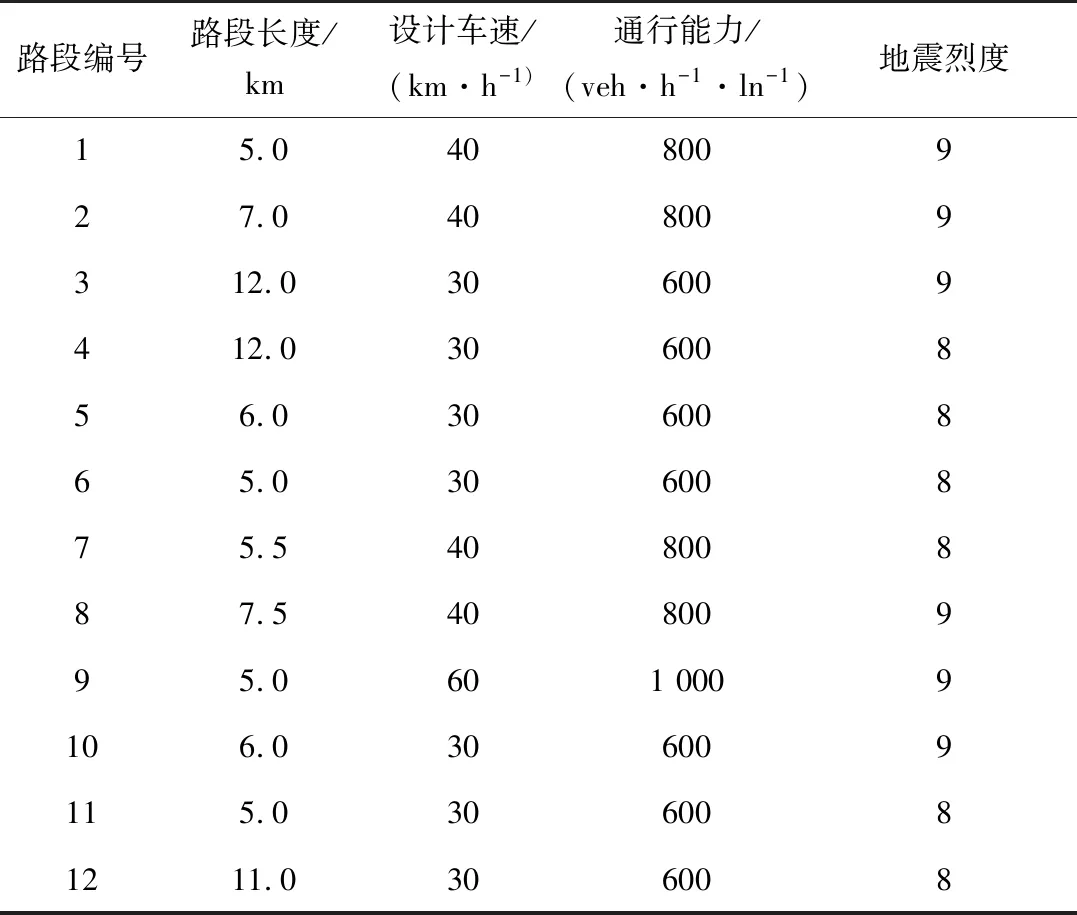
表4 路段基本信息[11]Table 4 Basic information of road section

3.2 路段及桥梁可靠性分析

在得到地震场对所研究路网的影响后，结合式(3)、表2及表3，可以计算得到路网中3个桥梁在设定地震影响下的连通先验概率，即可靠度值，如表5。

结合各个路段自身属性，每个单元路段的连通先验概率由式(1)、式(2)及表1所给出的参考系数计算可得。再根据式(4)及表5，计算出含桥梁路段的连通先验概率，结果如表6。

表5 桥梁基本参数[11]及连通先验概率Table 5 Basic parameters of bridge and prior connectivity probability

表6 路段震后连通先验概率Table 6 The prior connectivity probability of road section after earthquake

3.3 网络模型构建

以所研究的路网作为对象，基于贝叶斯网络模型建立道路网络结构模型，共有5个OD点对：OADB、OADC、OADD、OADE、OADF。共有26条路径，分别记为R1～R26。不同OD对之间的路径及其包含的路段如表7。

表7 路径及其所含路段Table 7 Path and its contained road sections

在网络模型中，路段以串联的形式构成路径，在某条路径中的任一路段失去连通功能后，整个路径便失去连通功能；而路径以并联的方式连接OD对，所有路径全部失去连通功能后才使得OD对之间失去连通功能。因此，利用GeNIe软件构建路网的贝叶斯网络模型，如图2。

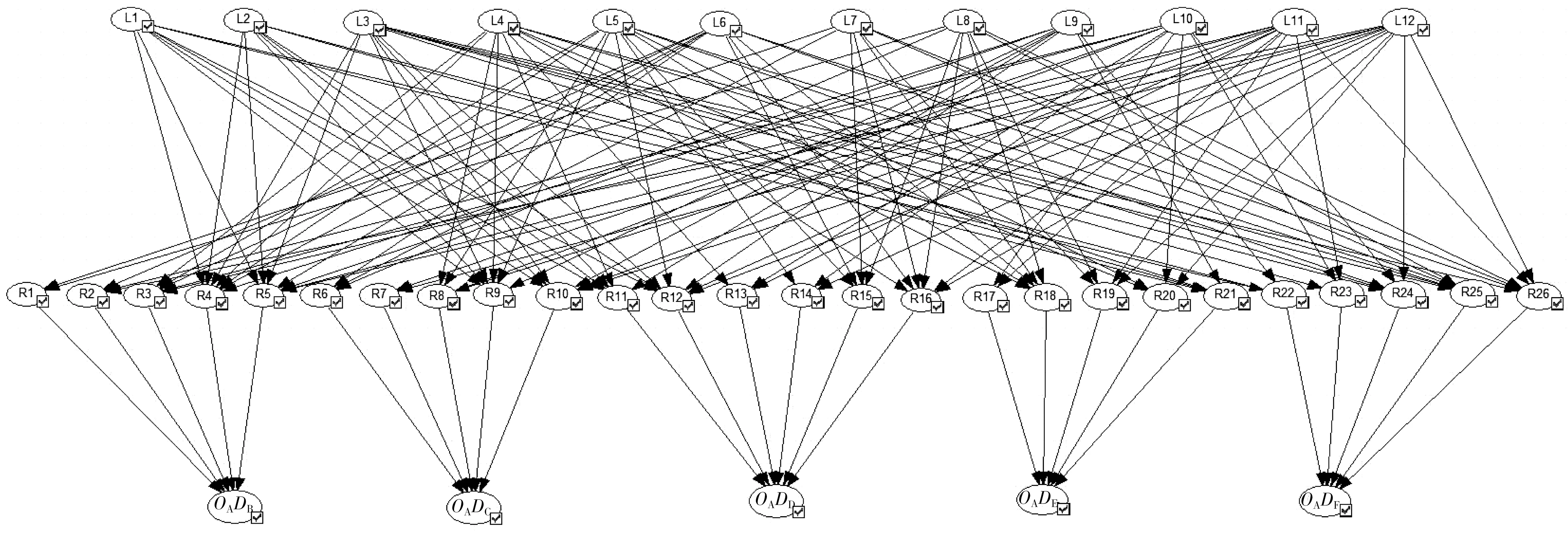
图2 路网的贝叶斯网络模型Fig.2 Bayesian network model of road network

3.4 网络模型求解

将12条路段在设定地震影响下连通的先验概率输入顶层节点中，求得26条路径在该情况下连通的先验概率。

在地震发生后，如某OD对之间所有路径均已中断，则无法完成在该OD对之间进行的运输调度任务。因此，在路径选择时应首先保证OD对之间保持连通，在此条件下，计算路网中26条路径的连通后验概率，以此作为评价路径可靠性的依据，具体数据如表8。

表8 路径连通先验概率及后验概率Table 8 Prior connectivity probability and posterior connectivity probability of path

3.5 运输调度决策分析

在进行震后运输调度时，应尽可能保证所选道路具有较高的抗震可靠性，同时在其他条件相近的情况下尽可能提高运输调度的效率。因此，笔者假设路线可靠性和运输时间的权重较高，结合设定地震参数及历史震害数据统计[17]，设定运输距离、路线可靠性和运输时间的权重向量γ=(γD,γP,γT)T。并假设每个路段每小时的通行量为300辆，即式(12)中fa=300，利用该式可求得12条路段的震后通行时间，从而得到26条路径的运输时间。

将运输时间、运输距离和路径连通后验概率结果依照式(9)～式(11)进行标准化处理，并利用式(13)计算各个路径的决策效用函数值，从而做出震后运输调度路径最优选。具体结果如表9。