不同理性预期下量子库诺特模型的动态演化分析
2021-06-19田英楠王嘉琪张新立
田英楠, 王嘉琪, 张新立
(辽宁师范大学数学学院,辽宁 大连 116029)
0 引言
量子博弈论是以量子信息论为主要工具研究博弈论的一门新兴交叉学科,最早由Meyer提出。由于量子博弈能解决很多经典博弈所不能解决的问题,所以提出之后就越来越受到国内外学者的关注,并被广泛应用于经济学、生物学、信息科学等诸多领域[1]。而寡头垄断是现实社会和经济中最普遍存在的市场结构,库诺特模型是寡头垄断的一种最基本模型。李慧等人[2]首次构造了一个“最小”量子结构来研究具有连续变量的量子库诺特博弈,后人在此基础上运用Li-Du-Massar方案对库诺特寡头模型进行了广泛量子化研究,譬如,YoheiSekiguchi等人[3]发现当纠缠度足够大时,不对称均衡全部消失;Lo等人[4]发现量子纠缠度越大,各个企业在纳什均衡点的利润越高;Du等人[5]发现在非对称信息的量子库诺特模型中,量子纳什均衡点利润是否高于经典纳什均衡点利润,与量子纠缠度、信息不对称程度相关;Zhou等人[6]发现在多人量子库诺特模型中,量子纠缠度趋于无穷大时,囚徒困境问题得以解决;Frackiewicz[7]发现不管逆需求函数与成本函数是否为线性,量子库诺特模型都只有一个纳什均衡解。
上述学者虽利用量子博弈论对库诺特寡头博弈模型进行了分析,得出一些新结论,但参与者都是完全理性的。在现实经济中,由于参与人认知的局限,企业采取完全理性行为规则是很难实现的。因此,许多学者又从放松理性假设角度对经典库诺特模型进行了分析研究。常见理性行为假设主要有:基本有限理性行为(一般简称有限理性)、延迟有限理性行为、适应性有限理性行为、天真预期行为等[8]。近年来,许多学者对具有不同预期的经典动态寡头博弈模型进行了研究。比如,Agiza和Elsadany[9]构建具有不同预期的双寡头模型(有限理性与适应性预期),给出了均衡解的稳定区域,并对复杂动力学现象进行数值模拟;于羽等人[10]构建具有有限理性与天真预期的库诺特寡头博弈模型,引入了产品差异性,研究了产品差异程度对纳什均衡稳定性的影响;张骥骧等人[11]构建具有不同预期的双寡头模型(有限理性与天真预期),分析了均衡解的存在性与稳定性,并用数值模拟研究了动态系统的稳定性与复杂现象;Hu等人[12]构建具有不同预期的双寡头模型(有限理性与天真预期),发现系统采用延迟反馈控制,会使系统从混沌状态变为稳定状态;黄萌佳等人[13]构建了具有知识溢出效应的不同预期双寡头模型(有限理性与适应性预期),对有限理性预期下的动态决策过程和系统的混沌复杂性进行研究。

1 量子库诺特模型

(1)
容易得到两企业的纳什均衡为
(2)

通过计算,γ≠0时,两企业的产量分别为
(3)

两企业的量子利润分别为
(4)
通过求出对πiQ关于xi的偏导,得到企业i(i=1,2)的边际利润:
(5)
解方程组(5),可得到两企业的量子纳什均衡为
(6)
2 不同理性的量子库诺特动态系统
由于寡头垄断市场信息的不完全性,每个企业掌握的市场信息并不充分,只可能做出有限理性决策。本文假设第一个企业是有限理性的,企业根据边际利润的信息决定产量,若t时期边际利润为正数(负数),则企业会在t+1时期增加(降低)产量,其模型可表示为
(7)
其中,α>0为第一个企业的产量调整速度。
假设企业2具有适应性预期,也就是t+1时期的产量由t时期的产量决策与t时期最优产量的加权平均共同决定,其模型可表示为
(8)

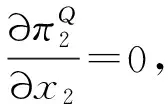
(9)
由式(7)与(8),可得到不同理性行为的两企业二维离散动力系统:
(10)
3 动态系统的量子均衡解与局部稳定性分析
令xi(t+1)=xi(t)=xi,得出复杂动力系统(10)对应的代数系统:
(11)
为了研究量子均衡点的局部稳定性,首先求出均衡离散动力系统的Jacobian矩阵,即:
(12)
其中,
根据系统均衡点的稳定性条件,当且仅当对应Jacobian矩阵的所有特征值|λi|<1,i=1,2,均衡点才是稳定的。因此,有如下结论:
定理1量子边界均衡点E1是不稳定的。
证明:点E1的Jacobian矩阵为:
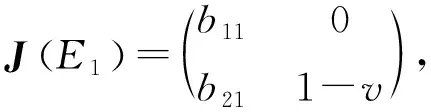
J(E1)的特征值分别为:λ1=b11,λ2=1-v,由于|λ1|>1,所以量子边界均衡点E1是不稳定的。
定理2量子纳什均衡点E2满足局部稳定性的充要条件:
(13)

J(E2)的特征多项式为p(λ)=λ2-Tr(J)λ+Det(J),其中Tr(J)表示迹,Det(J)表示行列式,且Tr(J)=2-v-2αcoshγ(beγ+ccoshγ)x′1,
由于Tr(J)2-4Det(J)>0,所以J(E2)的特征根为实数。|λi|<1,i=1,2的充要条件为Jury条件成立:1)1-Tr+Det>0,2)1+Tr+Det>0,3)Det-1<0。
利用模型假设可得:
显然条件(1)与(3)恒成立。条件(2)等于
化简即得E2的局部稳定条件。
4 数值模拟
为了更清楚地观察参数处于稳定域外所表现出来的复杂动态性特征,在本节运用Matlab对双寡头动态系统(10)进行数值模拟,描绘出单参数产量分岔图、最大李雅普诺夫指数图与对初始条件敏感性,从这几方面分析量子纠缠度与企业产量调整速度对系统稳定性及动态行为的影响。模型中的各参数赋值为a=10;b=0.6;c=0.5。
4.1 分岔与混沌分析
图1演示了v=0.7时,两个企业产量随α变化的分岔图与相对应最大的李雅普诺夫指数图。当γ=0时,量子纳什均衡点(3.575,3.575)在α<0.244 6保持局部稳定。随着α的增大,量子纳什均衡点不再稳定,并会产生分岔、混沌现象。当γ=0.2时,量子纳什均衡点(2.805,2.805)在α<0.263 5保持局部稳定。可见,随着纠缠度增大,系统(10)的稳定性就越高,出现分岔与混沌的可能性就越小。当系统李雅普诺夫指数为正数时,代表着发生混沌现象。比较γ=0与γ=0.2的情况,发现最大李雅普诺夫指数大于0与量子纠缠度呈现正相关性。

图1 v=0.7时,产量随α变化分岔混沌图与对应的最大李雅普诺夫指数图
图2演示了v=0.5时,两个企业产量随α变化的分岔图与相对应最大的李雅普诺夫指数图,发现分岔混沌现象与纠缠度之间的关系与v=0.7时相同。因此,纠缠度能增强系统(10)的稳定性,可以有效地控制分岔与混沌出现。

图2 v=0.5时,产量随α变化分岔混沌图与对应的最大李雅普诺夫指数图
奇怪吸引子是指时间趋于无穷大时,在任何一个有界集上出发的非定常流的所有轨道在其内部的一个集合,是混沌系统的主要特征之一。图3描述了不同纠缠度条件下,经过迭代10 000次对应图1混沌现象的奇怪吸引子,显示了α=0.37时的分形结构。

图3 α=0.37时对应图1混沌现象的奇怪吸引子
4.2 初始条件敏感性分析
混沌现象的一个重要特征就是对初始条件的敏感依赖性,为探究不同纠缠度条件下系统混沌状态对初始条件敏感性的影响,设两个企业的初始点为(x1(0),x2(0))=(3,3),相对微小变动的初始点(x1(0)+0.000 1,x2(0)),(x1(0),x2(0)+0.000 1),其中参数的取值为a=10;b=0.8;c=0.5;v=0.5;α=0.35。图4、图5分别为在不同纠缠度下,两个企业的产量随时间的变化图。初始值与微小的变动初始值对应的两条曲线在初期系统动态的演化都是无序状态且变化并不显著,但是随着时间推进,企业产量变化表现出明显的差异性。在相同初始值下,企业1比企业2产量的变动振幅大。随着纠缠度增加,产量随时间变化较为平稳,对初始值的敏感性较弱。因此,增大纠缠度可以减弱系统动态演化过程中初始条件的敏感依赖性。
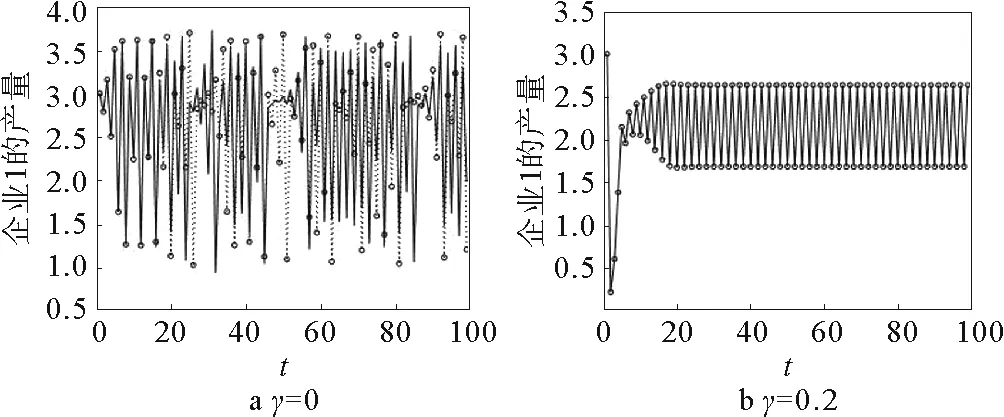
图4 公司1产量对初始条件的敏感性

图5 公司2产量对初始条件的敏感性
5 结语
本文将量子纠缠植入到不同理性预期条件下的量子库诺特动态博弈模型,在假定两个企业分别具有有限理性与适应性预期,成本函数为二次非线性,且具有相同的边际成本条件下,探究量子纠缠度、企业产量调整速度对均衡点稳定性与动态复杂性的影响,并对此模型进行了稳定性分析与数值模拟。结果表明,随着量子纠缠度的增加,系统稳定性会提升,产量调整速度增加至某一阈值时,会导致系统经过一系列分岔进入不可预测的混沌状态。系统进入混沌状态之后,任何初始条件的细微变动,都会引起产量发生激烈变化。量子纠缠度对控制系统的混沌状态起着重要的促进作用,从而使得企业可以选择稳定合理的产量。
