基于Backstepping的三轮机器人编队控制

于美妍，杨洪勇，孙玉娇

(鲁东大学信息与电气工程学院，山东 烟台 264025)

0 引言

多机器人在实际应用中发挥着越来越重要的作用，多机器人编队控制问题日渐成为学术界的研究热点。但由于机器人构造复杂，多机器人系统涉及的技术很多，人们比较常用的研究方法是把通信的多个智能体构成的计算系统即多智能体系统视为一个分布式网络，研究多智能体系统的分布式合作。文献[6]中针对具有干扰的多智能体系统的协同控制问题，提出了带有不匹配干扰和参数不确定的一致性控制算法。文献[7]研究了一类拓扑为循环图的多智能体系统在圆上运动的编队控制问题。文献[8]研究了具有比例加微分控制器的连续一阶多时滞多智能体系统的一致性问题。文献[9]研究了具有事件触发控制策略的二阶积分器多智能体系统的编队控制问题。文献[10]和[11]研究了混合阶多智能体系统的一致性问题。

在研究多智能体编队控制问题时，机器人的非线性系统往往比较复杂，直接得出整个系统的控制器存在一定的困难，而Backstepping方法是把系统进行分解，分别对每个子系统引入虚拟控制量，设计Lyapunov函数得到子系统的虚拟控制器，逐步反推得出系统真正的控制律，大大降低了系统设计的复杂程度，因此Backstepping方法被广泛应用于多机器人系统的控制过程中。文献[12]针对双轮驱动移动机器人，采用Backstepping思想设计了多机器人协同编队方法。文献[13]利用Backstepping方法，针对反馈混沌系统，提出了混沌同步一般控制方法。文献[14]研究的是无状态量测的不确定随机反馈系统，结合Backstepping思想，提出了一种自适应模糊控制方法。文献[15]针对模型不确定性不匹配的液压系统，利用Backstepping方法将扩展状态观测器和非线性鲁棒控制器综合起来。文献[16]首先对飞行器纵向模型分析,然后利用Backstepping思想设计了高超声速飞行器的模糊自适应控制器。

虽然机器人编队问题研究已久，但大多数文献都是针对机器人的线性运动特点进行研究，文献[17]结合事件触发策略，对一般线性多智能体系统的编队控制问题进行了研究。文献[18]研究了拥有一般线性动力学的分数阶多智能体系统编队控制问题。文献[19]对于具有有向交互拓扑的高阶线性群集系统的时变输出编队控制问题进行研究。Shi[20]等研究了存在时变时延和外部扰动等约束条件的高阶线性群系统编队控制问题。但是，现实世界很多智能体系统动力学方程并不满足线性特点，非线性系统在实际应用中占有很大比例，据我们所知，有较少文献对非线性多智能体系统进行研究。因此结合上述文献思想和控制器的设计方法，本文针对三轮机器人的非线性运动学特点，研究多智能体编队控制问题。本文的创新点主要有以下两点：1)基于机器人领航—跟随模型，构造了系统位姿误差运动学方程，将非线性系统编队控制问题改变成跟随者对虚拟领航者运动轨迹的追踪问题，有效地解决了基于领航—跟随模型的机器人编队存在的跟随者对领航者过于依赖的问题。2)运用Backstepping思想，构造了一个新的虚拟反馈误差变量，并基于这个误差变量设计了多机器人编队控制策略，实现了机器人对于预定轨迹的全局渐进稳定，降低了系统设计的复杂程度。

1 三轮机器人的动力学模型

在实际生活中，由于干扰等一系列因素存在，机器人的动力学模型会很复杂，为了便于后面的工作，本文做了几个假设：1)三轮机器人底盘上的3个轮子是间隔120°均匀分布，不考虑生产过程中出现的角度偏差。2)假定机器人行走的地面具有合适的摩擦力，机器人不会出现打滑的情况。3)由于一个机器人成品由很多复杂零件构成，将三轮机器人视为刚体以便分析。4)三轮机器人底盘重心与几何中心重合。

本文首先建立以底盘重心为原点的局部坐标系，如图1所示，以轮子A与B的角平分线建立x轴，逆时针90o建立y轴，(vxr,vyr,ωr)与(vxw,vyw,ω)分别是机器人在绝对坐标系与局部坐标系中的相关速度向量，Vv=[vAvBvC]T为3个驱动轮的线速度向量。θ=θw=θr为机器人转动的方位角，ω是三轮机器人的角速度，d是机器人底盘中心到轮中心的距离。

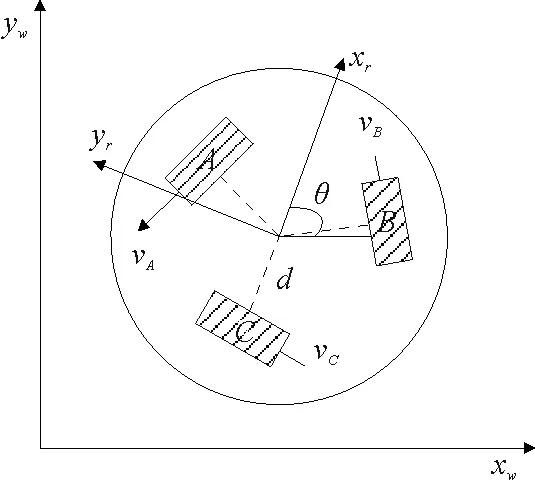
图1 三轮机器人数学模型

根据图1可得机器人动力学模型方程为

(1)

并且(vxr,vyr,ωr)满足式(2)

(2)

(3)

由图1，可以得到机器人3个轮子的速度变化公式为

(4)

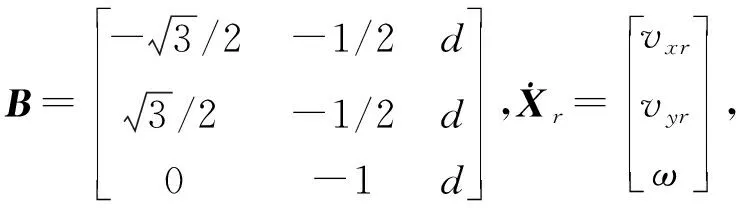
(5)

(6)

2 机器人的领导-跟随模型

基于领导-跟随模型的机器人编队的基本思想是在全部机器人中选择一个领航者，带领所有成员运动，其余机器人作为跟随者，跟踪领航者运动。领航者的移动轨迹是已定的，输入控制也只与自身的信息相关。

为了解决系统中跟随者对领航者的过度依赖问题，为每个跟随机器人分别设置虚拟领航者，并假设虚拟领航者的速度以及角速度始终与领航者保持一致。我们可以通过调整虚拟领航者与领航者之间的距离、角度来构造多智能体系统的编队队形，然后让跟随者按照设计的控制策略跟踪虚拟领航者的运动轨迹，实现编队目标。通过这种方法，本文将编队问题转变成跟随机器人对虚拟领航者的追踪问题。

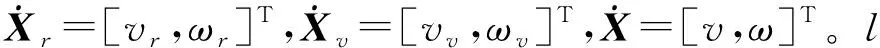
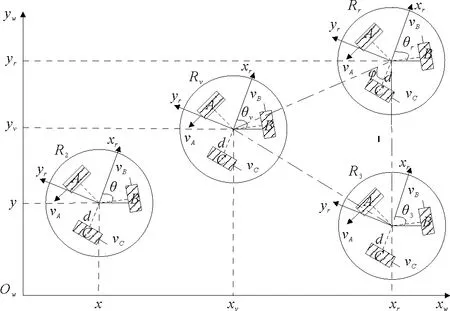
图2 基于领航—跟随模式的三角形编队结构

由Rr的位姿可以得到Rv位姿为

(7)

根据图2，得到跟随机器人R2对于虚拟领航者Rv的跟踪误差为

(8)

其中,ex，ey表示跟随者与虚拟领航者之间的x轴、y轴方向上的误差，eθ表示跟随者与虚拟领航者之间的角度误差。

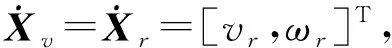
(9)

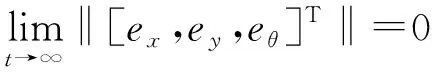
3 基于Backstepping控制器设计

定理1针对机器人动力学模型(1)，如果控制输入ω,v满足式(10)

(10)

其中,k1>0，k2>0，那么三轮机器人系统可以实现编队控制。

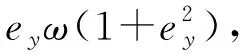
(11)

当eθ→0时，设计部分李亚普诺夫函数为

(12)

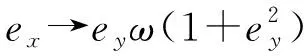
(13)

(14)

对式(14)求导得：

(15)

(16)

将式(11)、(16)代入式(15)得：

(17)

然后再将式(9)代入式(17)可得：

(18)

结合式(9)、(10)，对ω求导得：

(19)

代入式(18)，得：

(20)

将式(20)进行整理，得：

(21)

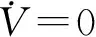
4 实验验证

在编队开始前，首先要确定的是多机器人系统运动所要保持的队形。常见的编队队形有直线形、三角形、矩形、五边形等。相对来说，直线形编队比较简单，其思想是确定好领航机器人运动轨迹，其它跟随机器人只需按照固定的距离跟踪即可。对于三角形、矩形、五边形编队队形稍微复杂一些，设计过程中，不仅需要控制好与领航机器人之间的距离，还要控制好两者之间的角度问题，来保证有规则的编队队形。

本文基于领航—跟随的方法对理论结果进行验证，分别对多机器人系统的矩形编队、三角形编队、五边形编队进行仿真。

4.1 参数设置

在进行所有编队时，均设定k1=1.5，k2=2，领航机器人的初始位姿L0=[2,0,π/3]；领航者速度Lv=4，角速度Lω=2。

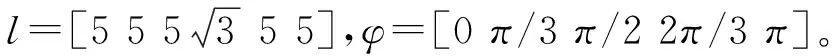
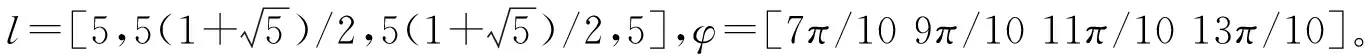
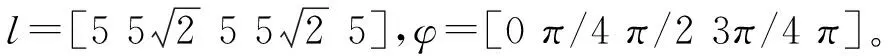
4.2 编队仿真

基于上述参数设置，对系统进行仿真，得到的实验结果如图3～图5所示。

图3 机器人保持三角形编队相关结果图

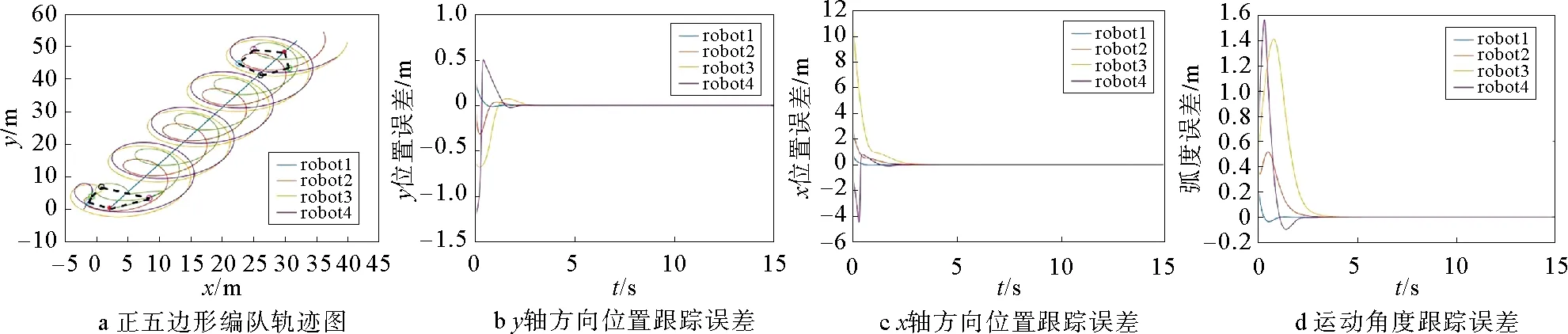
图4 机器人保持正五边形编队相关图

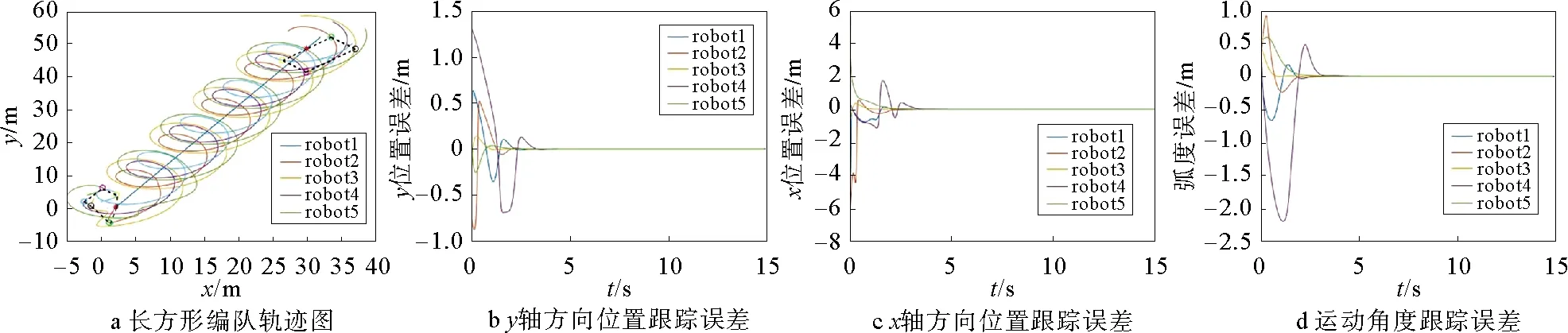
图5 机器人保持长方形编队相关图

图3a领航机器人沿直线运动，5个跟随者机器人与领航机器人要进行三角队形编队。其中“*”表示领航机器人，“o”代表跟随机器人。图中给出了时间在1 s、14 s时各机器人编队情况。由图3a可以看出，在刚开始一段时间内跟随机器人并未跟踪上领航者机器人，系统没有达到稳定，后期6个机器人维持规则的正三角队形持续移动，说明跟随机器人追踪上领航机器人。

图3b和3c为三角形编队时的系统位置、角度误差图，其中蓝、红、橘黄、紫、绿线分别表示跟随机器人1～5的位姿状态，可以看出，在控制器的控制下，随着时间的推移，位置以及角度的跟踪误差在4 s内收敛到0，表明了系统达到渐近稳定，证明控制器可以进行有效控制。

图4a为4个跟随机器人与领航机器人形成正五边形编队轨迹效果图，与图3a类似，开始的一段时间，机器人并未保持规则五边形运动，后期，跟随机器人追踪上领航机器人，保持规则正五边形运动。

图4b和4c是进行正五边形编队的误差系统示例图，由图可以看出智能体大约在3 s时，跟随者与虚拟领航者在x轴、y轴方向上的位置误差，以及角度误差便趋于0，达到控制器设计目标。

图5a为跟随者机器人与领航机器人运动形成的矩形编队队形，由图5a可以看出，在1 s时跟随机器人并未跟踪上领航者机器人，各机器人没有保持矩形轨迹运动，但是轨迹在逐渐趋于规则，14 s时，各跟随机器人已经追踪上领航机器人并保持编队队形持续运动。

图5b和5c为矩形编队时，跟随机器人与各自领航机器人的误差图，根据图示，与图4b和4c类似,智能体大约在3 s时,误差系统就已经为0，说明此时跟随机器人与领航机器人已经保持编队队形运动。

5 结语

本文基于Backstepping方法对三轮机器人编队控制问题进行研究，提出了新的机器人编队控制策略。通过仿真实验可知在控制器的作用下，机器人逐渐形成三角形、矩形、正五边形编队，并以很小的误差保持队形持续运动。下一步工作将对具有外部干扰、通信时延等影响的三轮机器人编队控制问题进行研究。