一类具有异维节点的复杂动态网络外同步控制

方荣东，王银河，汤 晓

(1.广东工业大学自动化学院,广州 510006;2.中科启迪光电子科技(广州)有限公司,广州 510006)

0 引言

综合以上分析，本文针对具有不同拓扑结构和非线性耦合函数的两个复杂动态网络，在其节点动态及状态维数均不同、耦合强度未知的情况下，着重两个网络连接强度之间的误差估计，利用处于不同网络中对应节点间的相似动态行为设计广义外同步自适应控制器。与现有文献相比，本文的优势在于不需要网络满足通常的耗散条件，同一网络内的节点动态及其状态维数允许不同，并且所设计的自适应控制器的结构更加简单明了。

本文首先描述了一类节点异维且耦合强度未知的驱动响应网络，并提出广义外同步定义和相关假设。然后借助两个网络对应节点具有相似动态行为的条件，结合lyapunov稳定性定理进行驱动响应网络广义外同步控制设计和分析，得到了自适应同步控制器及连接强度之差估计的自适应律。最后通过数值仿真验证了本文方法的有效性。

1 模型描述和基本假设

考虑如下驱动网络X和响应网络Y，它们分别由N个不同节点组成，其节点的动态方程分别表示为

(1)

(2)

其中,xi=(xi1,xi2,…xini)T∈Rni和yi=(yi1,yi2,…yimi)T∈Rmi分别是驱动网络(1)和响应网络(2)第i个节点的状态向量，ni和mi分别是节点i的状态维数，Ai∈Rni×ni和Bi∈Rmi×mi分别是节点i的系统矩阵，hij(xi,xj)∈Rni和pij(xi,xj,yj)∈Rmi(i,j=1,2,…N)是光滑的非线性向量函数，表示同一网络的节点间的内部耦合关系，C=(cij)N×N和D=(dij)N×N分别是驱动网络X和响应网络Y的外部耦合结构矩阵，反映网络的拓扑结构和耦合强度。

假设1在驱动网络(1)和响应网络(2)中，网络的拓扑结构矩阵C和D的元素是未知的，即节点间的耦合强度cij，dij都是未知的常数，同时C和D不必满足网络耗散条件。

注1:在驱动网络(1)和响应网络(2)中，属于同一网络的节点其状态维数可以不同，两个网络对应节点的维数也可以不同。另外，假设1意味着本文涉及的网络模型(1)和(2)更具一般性。

假设2存在N个非零实矩阵Si∈Rmi×ni，使得

SiAi=BiSi,i=1,2,…,N

(3)

注2：方程(3)表明驱动网络(1)和响应网络(2)中的系统矩阵Ai和Bi至少有一个相同的特征值，这意味着，驱动网络的第i个标称节点和响应网络的第i个标称节点有相似的动态行为，本文将这两个对应节点称作相似节点，Si称作相似参量。显然，这两个节点的状态维数可以不同，另外，当已知Ai和Bi时，利用矩阵的拉直运算性质[28]，方程(3)中的相似参量Si可由式(4)代数方程解得：

(4)

其中，vec(·)表示矩阵按列拉直后的向量，A⊗B表示矩阵A和B的Kronecker积。

假设3存在函数Hij(xi,xj)∈Rmi×mj(i=1,2…,N)满足:

Sihij(xi,xj)=Hij(xi,xj)Sjxj,pij(xi,xj,yj)=Hij(xi,xj)yj

(5)

并且Hij(xi,xj)是范数有界的，即存在正数M使得‖Hij(xi,xj)‖≤M。

注3:方程(5)表明驱动响应网络各自的内耦合函数之间也有某种相似关系，其中一个特例是若存在函数ψij(xi,xj)∈Rni×mj使得hij(xi,xj)=ψij(xi,xj)Sjxj成立，那么Hij(xi,xj)=Siψij(xi,xj)满足(5)。

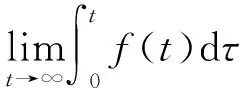
定义1考虑驱动网络(1)和响应网络(2)，若存在相似参量Si∈Rni×ni(i=1,2,…,N)，使得

(6)

则称网络(1)和网络(2)实现了广义外同步。

注4：定义1可以表示多种不同类型的外同步，例如当S1=S2=…=SN=Ini时，表示完全外同步，此时两个网络对应节点的状态维数相等，即ni=mi，但此时每个网络内节点的维数仍然可以不同；当S1=S2=…=SN=αIni(其中0≠α∈R)，表示投影外同步。

2 外同步控制设计

本文的控制目标是为响应网络(2)的每个节点设计合适的控制器ui，i=1,2,…,N，使其与驱动网络(1)实现广义外同步。

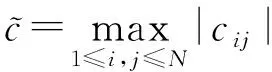
为实现外同步控制目标，提出如式(7)自适应控制器:

(7)

其中，fij表示不同网络中对应节点连接强度误差ωij=cij-dij的估计值，gi为控制增益，fij的自适应律和增益gi的更新律分别为

(8)

(9)

其中，ki为任意正常数，i=1,2,…,N。

注5：由式(7)～(9)可以看出，与文献[18]相比较，本文所设计的自适应控制器结构更加简单明了。

利用误差ei=yi-Sixi(i=1,2,…,N)以及式(1)、(2)和(7)～(9)，可以得到误差系统:

(10)

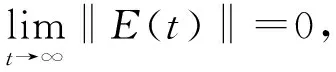
证明:考虑正定函数(11)

(11)

利用式(7)～(10)，函数V(t)关于时间t的导数为

(12)

将式(5)代入式(12)可得:

(13)

从而

(14)

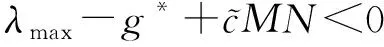
(15)

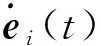
注6:使用定理1时需要检验前提条件：

步骤1：针对网络模型式(1)和(2)，在耦合强度cij，dij都是未知常数的情况下，确定自适应律(8)、增益更新律(9)和控制器(7)。

步骤2：利用式(4)求出满足式(3)的相似参量Si，i=1,2,…,N。

步骤3：利用步骤2中的结果验证假定3是否成立，若成立，则利用步骤1中的自适应控制器作用于网络(2)，从而实现外同步。

3 数值仿真

考虑驱动网络(1)和响应网络(2)各由5个节点组成，系统矩阵Ai和Bi分别为

上列矩阵表明驱动网络(1)和响应网络(2)不仅同一网络内节点的维数不完全一样，两个网络对应节点i的维数也不相同。拓扑结构矩阵分别选择为

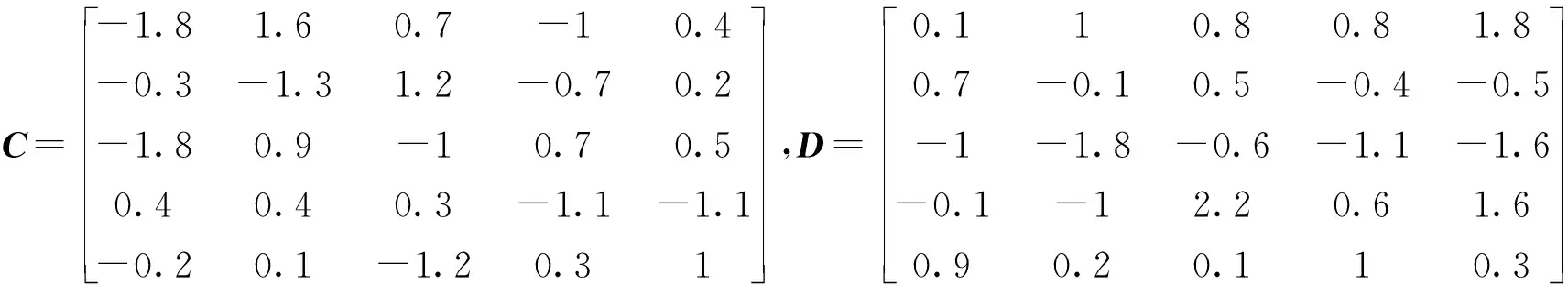
在假设2中已给出了相似参量Si的算法，本文将它们选择为

基于注3，函数ψij的选择为

由此可得驱动网络(1)节点间的耦合函数为hij(xi,xj)=ψij(xi,xj)Sjxj，响应网络Y节点间的耦合函数为pij(xi,xj,yj)=Hij(xi,xj)yj，系统状态初值xi(0)和yi(0)及控制参数初值fij(0)和gi(0)随机产生，自适应控制器形式由式(7)～(9)给出。

仿真结果如图1～图5所示，其分别为参数ki=100(i=1,2,3,4,5)时驱动响应网络节点xi和yi的状态收敛曲线，误差ei和控制器ui的参数gi及参数fij(i,j=1,2,3,4,5)随时间变化的响应曲线。

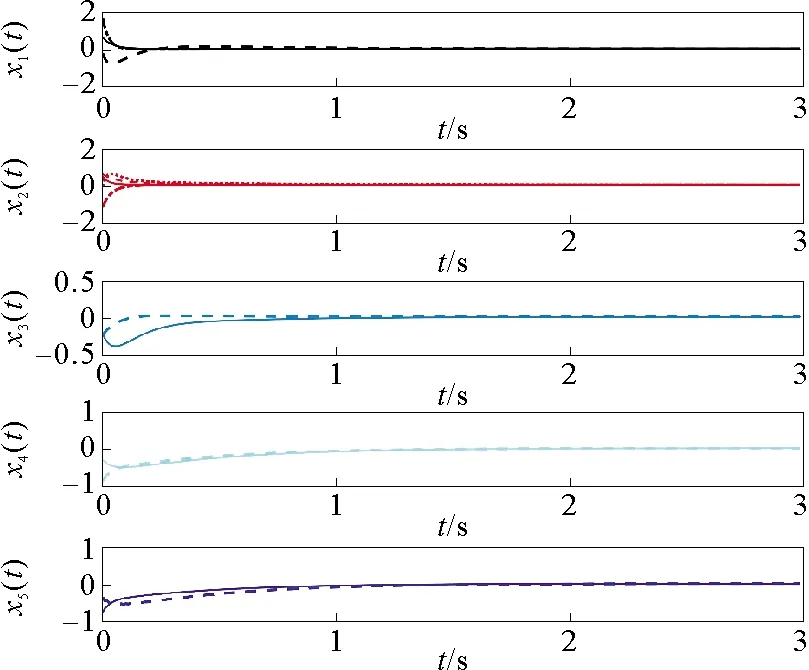
图1 ki=100时，节点xi(i=1,2,3,4,5)的状态响应曲线

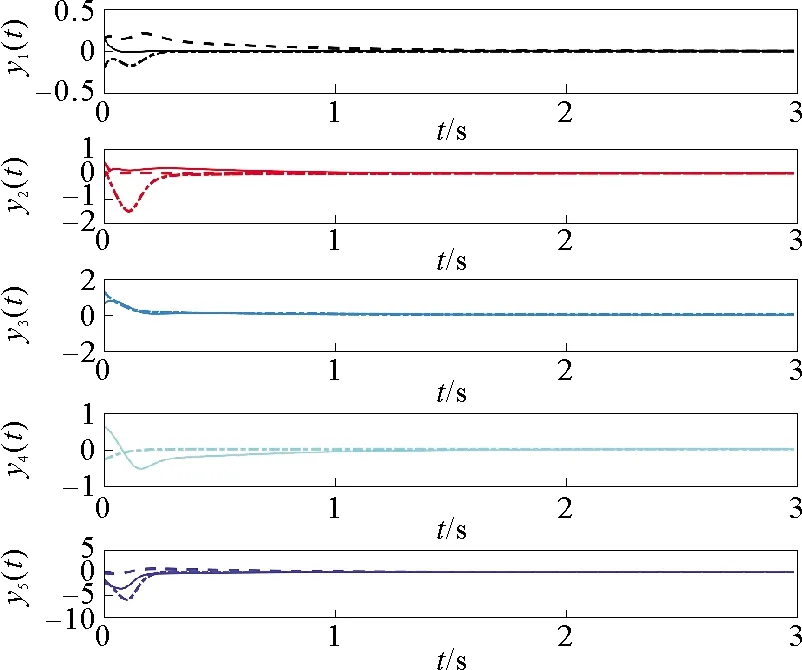
图2 ki=100时，节点yi(i=1,2,3,4,5)的状态响应曲线

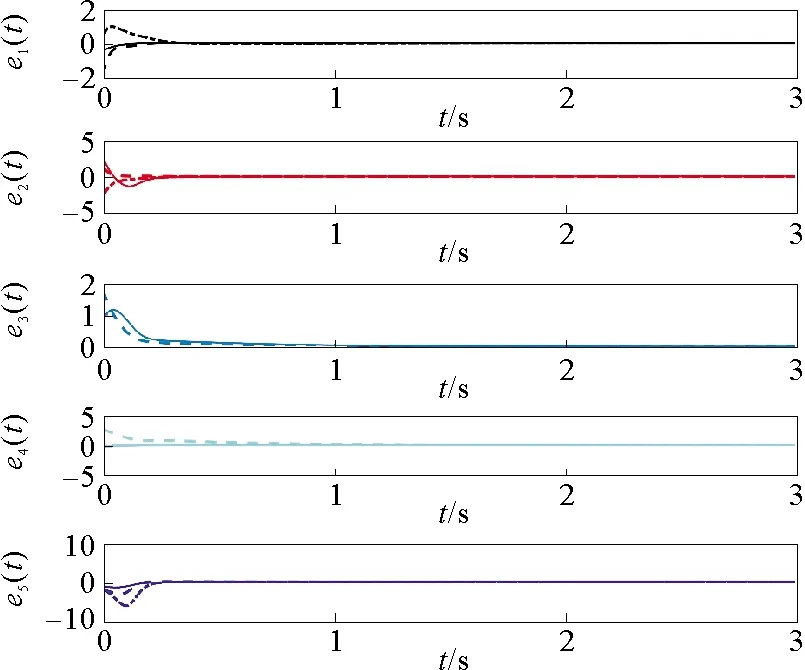
图3 ki=100时，误差ei(i=1,2,3,4,5)的响应曲线

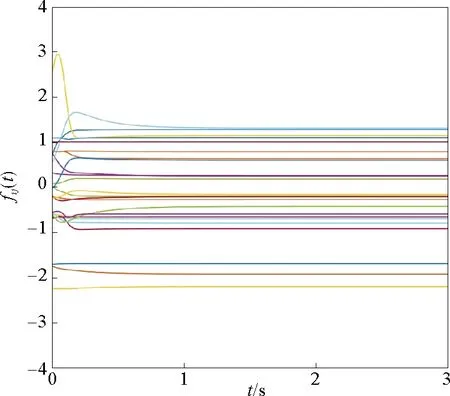
图4 ki=100时，自适应律fij(i,j=1,2,3,4,5)的响应曲线

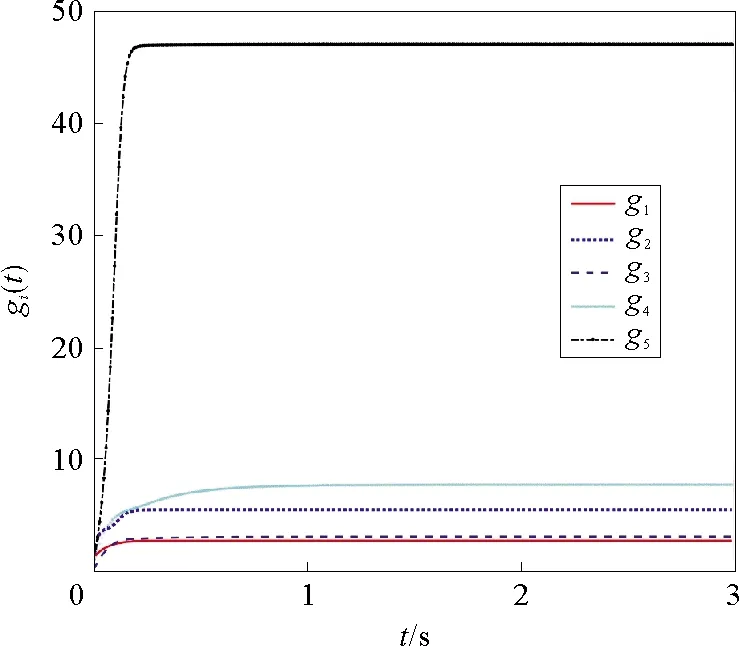
图5 ki=100时，控制增益gi(i=1,2,3,4,5)的响应曲线

由图1～图3可以看到两个网络对应节点的状态误差ei(t)(i=1,2,3,4,5)逐渐趋于0，即驱动网络(1)和响应网络(2)实现了广义外同步；由图4、图5可知自适应估计值fij和控制增益gi(i,j=1,2,3,4,5)都是有界的。上述仿真结果表明，本文提出的自适应控制器可有效实现驱动响应网络的广义外同步。

4 结语

本文针对一类驱动响应网络广义外同步问题，通过利用两个网络对应节点间的相似性，在拓扑结构不同和耦合强度未知的情况下，使用自适应律估计两个网络中对应节点耦合强度间存在的差异，并利用估计信息和网络中对应节点间的相似性辅助设计自适应外同步控制器，结果表明网络间的相似性有助于简化控制设计，所设计的控制器结构简单明了，最后用数值仿真验证了该控制器的有效性。但本文仅探讨了网络孤立节点是线性且耦合无时滞的情形，而现实工程中非线性系统和时滞系统也是广泛存在的，因此我们将在今后的研究中继续探究包含非线性孤立节点以及具有时滞的复杂动态网络外同步控制问题。