高超声速飞行器实时最优伪谱反馈末制导算法研究
2021-06-19司维超黎志强
宋 超,司维超,黎志强
(海军航空大学,烟台,264001)
0 引 言
高超声速飞行器经过远距离、长时间滑翔飞行后到达目标区域,开始执行作战任务。作为飞行器再入飞行的最后阶段,末攻击段的制导效果直接影响到作战任务的成败。
针对攻击目标移动的特点,再入攻击末制导多采用预测校正制导方法[1~3]。文献[1]研究了一种基于负加速度的预测校正制导方法,该方法首先获取阻力加速度剖面模型,通过数值预测,得到阻力加速度与航程的关系实时校正从而消除航程偏差。文献[3]采用基于航路点的预测校正制导方法,将整个轨迹分为预测校正阶段及在线生成跟踪阶段,在线生成新的可行参考轨迹。虽然预测校正制导不依赖于预先装订的轨迹,但仍存在两个问题:一是轨迹优化算法大多需要耗费计算机时,难以实现在线实时计算;二是算法执行过程中出现的误差难以在线实时修正。
而近年,伪谱反馈算法在各种导航、制导与控制问题中得到了有效的应用,如航天器转向机动[4]、实时最优控制稳定性分析[5]、最优反馈制导[6]等。文献[5]给出了2种基于Radau伪谱的实时反馈控制算法,在自由采样情况下,对闭环系统的稳定性进行分析,并应用到了机械臂及倒立摆的控制问题中。文献[6]给出了基于hp自适应伪谱法的实时最优反馈控制方法,并将其应用到轨迹优化领域中。文献[7]利用最优反馈控制和轨迹快速重构技术,设计一种有限推力空间远程变轨自适应闭环制导方法。
为满足飞行器在线实时计算的要求,本文将利用伪谱反馈算法对飞行器末制导方法进行研究。首先,给出了一种在线求解非线性最优控制问题的算法;然后,证明了该算法的收敛性;最后通过分别对固定目标及移动目标进行仿真,验证了所提方法的有效性。
1 实时最优伪谱反馈末制导算法
实时最优伪谱反馈算法的应用过程如图1所示。具体的算法步骤描述如下:
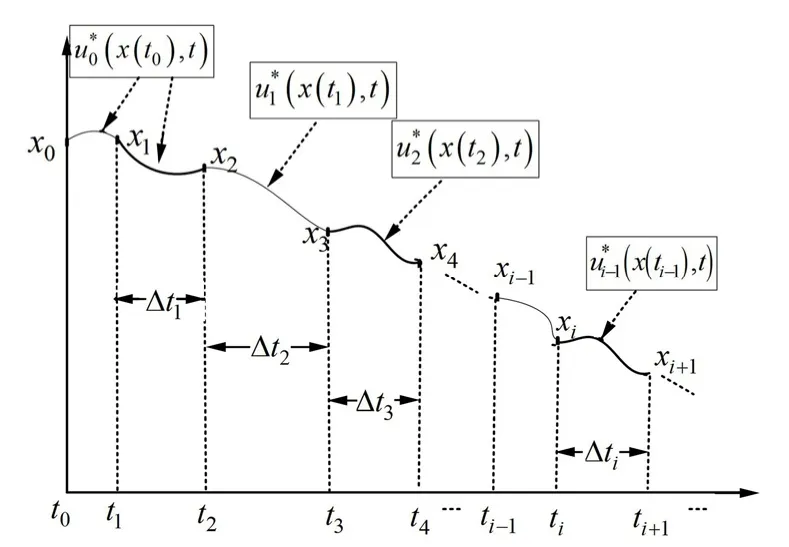
图1 伪谱反馈连续应用过程Fig.1 Pseudospectral Feedback Application Process
a)步骤1:选定节点个数N、第1次优化时刻1t,初始状态x0及终端状态xf,应用GPOPS离线计算最优控制量,生成最优轨迹。
b)步骤2:计算t1时刻的状态为x1=x1(t),在[t0,t1]时间段内,将u0*(x(t0),t)应用于轨迹控制上,令i=1。
c)步骤3:在时间段[ti,ti+1]内,根据上步计算的ti时刻的状态值xi和终端状态值xf,应用GPOPS实时计算最优控制量,t∊[ti,tf],生成ti时刻点至终点的最优轨迹;而在此时间段内,作用在系统上的控制量是。设Δti为优化时间,则ti+1=ti+Δti。
d)步骤4:令i=i+1,返回步骤3。
以u2*(x(t2),t)为例,来说明伪谱反馈末制导算法的实施过程:用u*2(x(t2),t)表示以t2时刻状态量x2为初始状态、xf为终端状态,应用GPOPS优化生成最优轨迹时所需的系统控制量,记所需的优化时间为Δt2,在此期间,作用于系统上的最优控制为前一次优化过程得到的控制量u1*(x(t1),t),而在t2+Δt2=t3时刻后,最优控制量u2*(x(t2),t)才被应用于系统上,且应用时间的长短取决于以x3为初始状态、xf为终端状态,优化计算新的最优轨迹所需的时间。
2 算法收敛性分析
定义实际系统动力学方程为
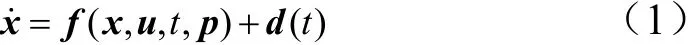
式中p为实际系统参数;d(t)为外部干扰输入。
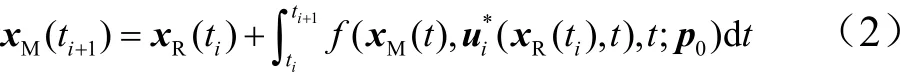
式中xR为实际系统状态量;xM为理想的系统状态量;p0为系统参数初始值;t为控制量作用时间。

因此,t=ti+1时刻系统的状态决定于控制量的作用,即:

由于存在计算时间延迟及干扰d(t)和不确定性p的影响,实际系统状态量xR与理想的系统状态量xM之间存在偏差。将式(4)减去式(2)得:
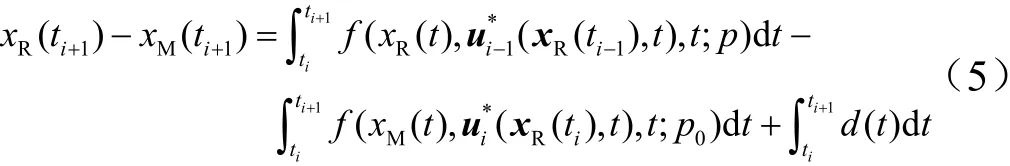
假设1:对于任意状态量x,函数f(x,u,t;p)是利普希茨(Lipschitz)连续的,则式(5)可写成:
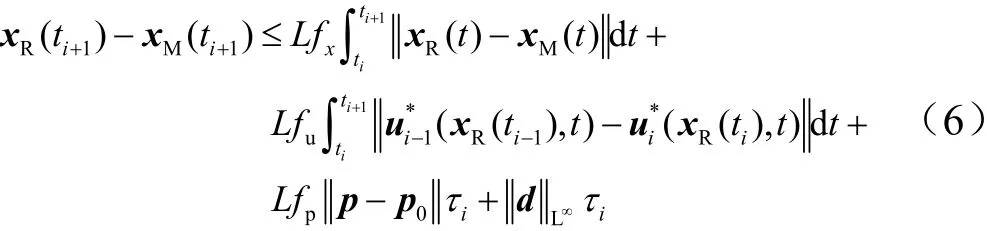
式中L为函数的Lipschitz常数。
引理1:(Gronwall 定理[8])令y(t)R+∊是满足如下Gronwall不等式的可积函数:
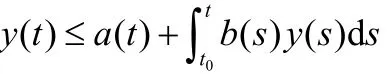
式中a,b为连续非负有界函数,且a(t)在[t0,tf]时间内非减。则有下式成立:

令δ>0是使得下式成立的最小值:

式中αi∊(0,1)且。则有下述结论成立:
定理1:对任意ε>0,若计算时间满足:

证明:由式(6)至式(9)可得:
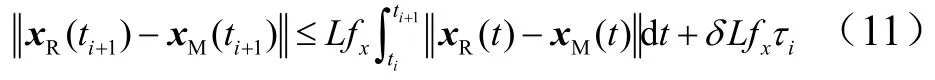
则由引理1,式(11)化为:
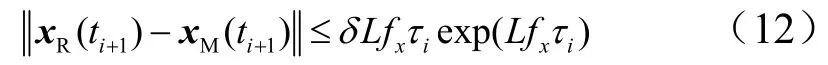
由Lambert W函数定义可知,对y,z∊R+,若z≤W(y),则有zez≤y。因此,由式(10)和式(12)可得:
3 仿真研究
高超声速飞行器无动力运动方程见参考文献[9]。各变量的限制为
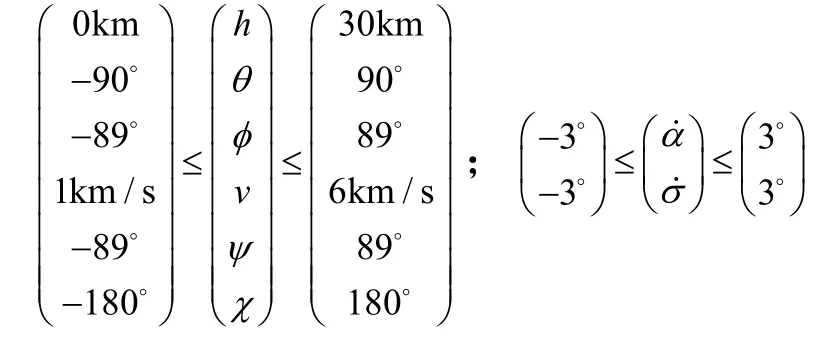
式中h,θ,φ,v,ψ,χ分别为高度、经度、纬度、速度、航迹角、航向角,均为状态量;α,σ分别为攻角、倾斜角,为控制量。
设飞行器再入初始值如表1所示。

表1 飞行器状态初始值Tab.1 Initial Value of Aircraft State
3.1 目标位置固定
假设地面固定目标位置:经度为5°,纬度为3°。为提高末攻击段的制导精度,引入终端约束为
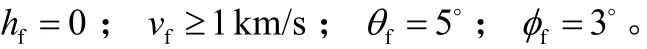
仿真结果见图2至图9。
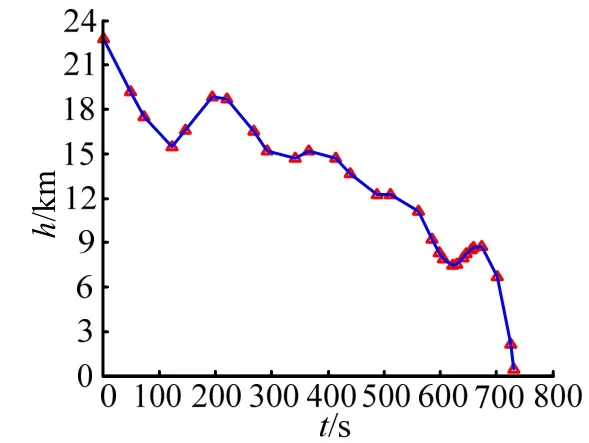
图2 高度变化曲线Fig. 2 The Curve of Height
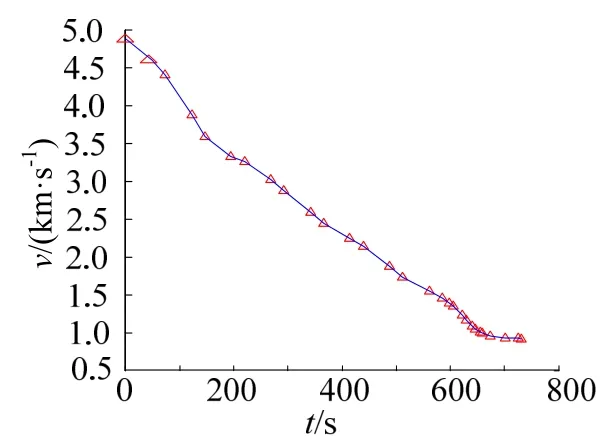
图3 速度变化曲线Fig.3 The Curve of Speed
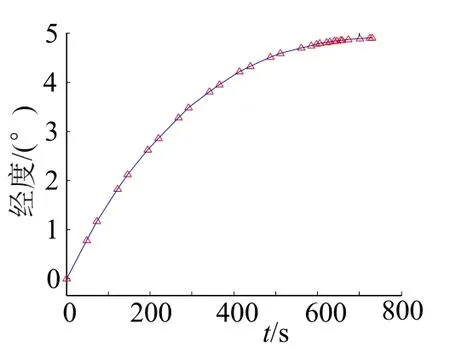
图4 经度变化曲线Fig.4 The Curve of Longitude
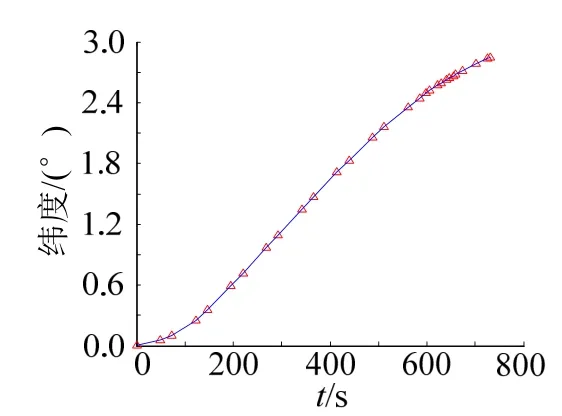
图5 纬度变化曲线Fig.5 The Curve of Latitude

图6 航迹角变化曲线Fig.6 The Curve of Flight Path Angle
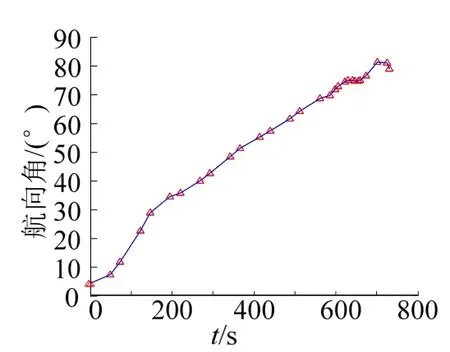
图7 航向角变化曲线Fig.7 The Curve of Azitude Angle
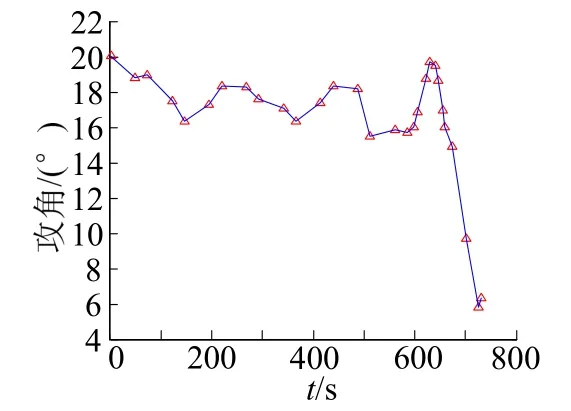
图8 攻角变化曲线Fig.8 The Curve of Attack Angle
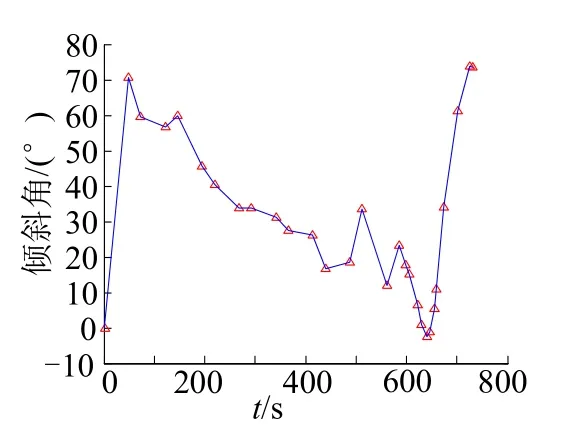
图9 倾斜角变化曲线Fig.9 The Curve of Bank Angle
从图2至图9可以看到:终端约束条件得到满足,高度、速度和航迹角均在设定的约束范围之内;且飞行器最终准确攻击到位于(5°,3°)的目标点。
3.2 目标机动
目标由于机动,其位置并非时刻精确已知,而是通过卫星、地基雷达、预警机等侦查预警系统和飞行器的机载雷达或红外传感器等设备探测。当目标信息传输给飞行器,飞行器将根据新的末端位置,应用伪谱反馈制导算法生成新的最优再入轨迹。目标未知信息校正次数越多,攻击命中精度越高。算法流程如图10所示。

图10 攻击机动目标制导算法流程Fig.10 Guidance Algorithm Flow Chart of Attacking Maneuvering Target
不失一般性,本文对目标位置进行3次校正,并仿真比较其落点偏差。
假设移动目标初始位置为:经度5°,纬度2°。沿着经度线做匀速运动,速度为37.04 km/h。
从图11、图12可见,飞行器通过伪谱反馈制导方 法可以修正由于目标移动带来的落点偏差。且校正次数越多,制导精度越高。但是制导时间也会相应增加。制导误差对比如表2所示。
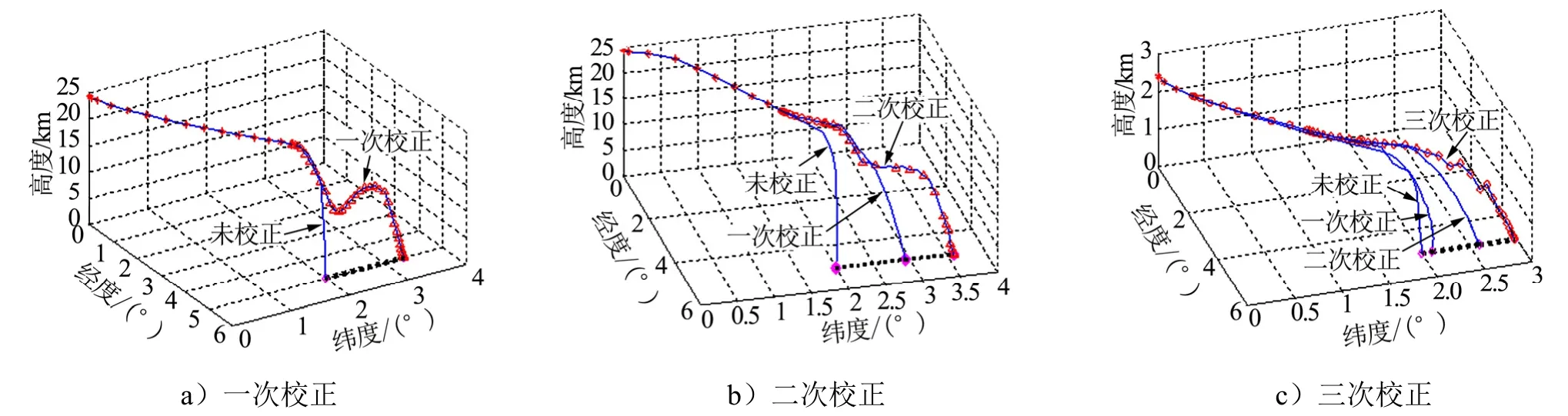
图11 校正的三维轨迹Fig.11 Three-dimensional Trajectory of Adjusting Once
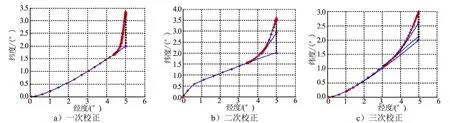
图12 三维轨迹的地面投影Fig.12 Ground Projection Figure of Adjusting Once
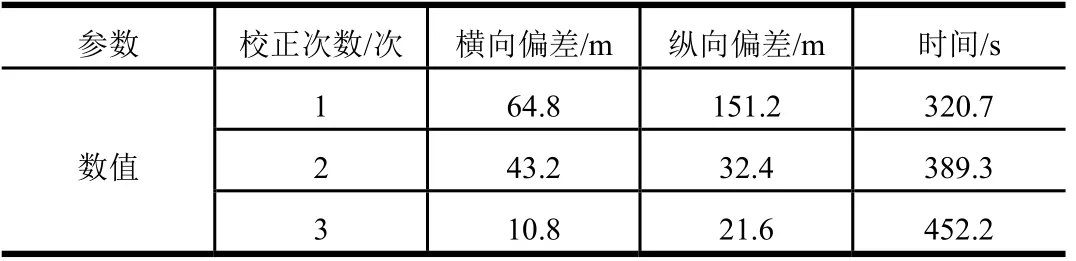
表2 制导误差对比Tab.2 Guidance Error Constrast
4 结束语
本文针对飞行器攻击机动目标的任务要求,提出了一种伪谱反馈实时最优制导方法,并从理论上证明了该算法的收敛性。通过仿真可以看出,攻击固定目标时,该方法能引导飞行器准确飞向目标;当目标慢速机动时,制导精度随着目标位置的校正次数增多而增高。仿真验证了伪谱反馈制导方法的可行性和优越性。
