复杂三维走向三铰链管路补偿工况下的补偿器角位移研究

吴立夫，吴云峰，张 萌，刘 艳，丁建春

（1. 北京宇航系统工程研究所，北京，100076；2. 深低温技术研究北京市重点实验室，北京，100076）

0 引 言

作为贮箱增压和推进剂运送的通道，液体运载火箭管路系统除满足基本的输送功能外，还需要适应箱体、壳段以及发动机系统的制造误差和工作变形，对不同的边界位移进行补偿。目前管路系统的补偿可通过自补偿和补偿器补偿两种方法实现[1]。自补偿方法利用管路自身的弹性变形实现补偿，而补偿器补偿方法则需要借助膨胀节或补偿管等结构进行补偿[2]。新一代运载火箭采用液氢、液氧或者液氧、煤油作为工质。随着火箭贮箱直径的增加、工质温度的降低，加注、增压等工况下贮箱变形量显著增加，因而对管路系统提出了更高的补偿需求。为满足大补偿量的管路设计要求，新一代运载火箭管路系统通常采用三铰链管路作为补偿导管。研究表明，采用三铰链式管路补偿方案时，管路结构能够很好地适应较大轴向和横向位移工况，且产生的支反力较小[3,4]。

运载火箭三铰链管路中包含3个方向铰链补偿器，各铰链补偿器的变形能力决定了管路的整体补偿能力。因此在三铰链管路方案设计时，一项重要的工作即为评估补偿工况下管路中各铰链补偿器角位移，确保其不超过补偿器最大变形量要求。

对于结构相对简单的平面三铰链管路，将其简化为包含3个铰链的杆件系统后，可通过几何方法对管路变形时各铰链补偿器的角位移进行理论计算[5,6]。在计算空间三铰链管路的补偿器变形时，部分研究[7,8]采用了平面简化的方法：首先将空间管路化简为2个正交平面内的平面管路，在上述平面内分别计算补偿器角位移分量后，通过角度合成获得最终结果。

对于具有复杂三维走向的空间三铰链管路，通过上述平面简化方法计算补偿器角位移时难免引入较大建模误差，此时需要开发更准确的理论计算方法。除此之外，更为便捷的方法是通过有限元仿真[9]或静力加载试验[10]，对与管路在补偿工况下的结构变形进行模拟或复现，进而提取或测量各个补偿器的变形角度。

本文选择某型号三铰链自生增压管为研究对象，分别采用自研理论计算方法、有限元仿真方法和静力试验方法对拉伸补偿工况下管路中3个铰链补偿器的变形情况进行评估，并对3种方法的实施过程和结果进行了对比分析。

1 方法和原理

1.1 自研理论计算方法

考虑到自生增压管结构的复杂性，本文采用自研理论计算方法对补偿器角位移进行分析。与常规的平面简化方法不同，自研理论计算方法首先建立了三铰链管路的通用几何模型，如图1所示。模型中3个铰链补偿器的编号分别为1#、2#、3#。以铰链中心为边界，可将管路分为A、B、C、D4段，其中A段、D段管路的末端分别为边界A0和D0。位移边界条件通常施加于A0和D0端。

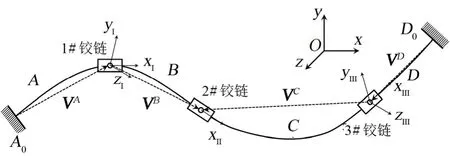
图1 空间三铰链管路的几何模型Fig.1 Geometric Model of a Three-hinge Pipe with Three-dimensional Route

假设管路中铰链补偿器的刚度远小于各管段的刚度，可将管段简化为刚体，并使用4个空间矢量VA、VB、VC和VD描述其位置关系。空间矢量的初始值可通过管路的几何构型确定。对于发生补偿变形的管路，将1#、3#铰链补偿器的角位移参数θ1、θ3设置为自变量。由于每个铰链补偿器包含2个自由度，因此θ1、θ3各包含2个分量。结合各空间矢量的初始值以及补偿边界位移，可分别通过θ1、θ3计算补偿变形后各管段空间矢量的值，记为V′A(θ1)、V′B(θ1)以及V′C(θ3)、V′D(θ3)。利用2#铰链补偿器处管路连续的条件，可构建关于θ1、θ3的方程组：

式中X0A、X0D为边界A0、D0的初始位置，u0A、0Du为管路A0、D0端的线位移矢量

式（1）包含3个方程，不足以求解θ1、θ3的4个分量值，此时可结合最小变形能原理建立补充方程。假设3个铰链补偿器刚度一致且发生弹性变形，其角位移幅值分别为Θ1、Θ2、Θ3，则真实的θ1、θ3应使得铰链补偿器的总变形E能达到最小值，即：

式中K为各铰链补偿器的刚度；Θ1、Θ3可分别由θ1、θ3计算得到，Θ2可由B、C管段变形前后的空间矢量VB、VC、V′B(θ1)和V′C(θ3)计算得到。由此可见，(Θ21+Θ22+Θ23)

也是θ1、θ3的函数，采用最小二乘法，可将式（2）转化为4个关于θ1、θ3分量的方程作为补充方程。

求解由式（1）以及补充方程构成的条件极值问题可确定θ1、θ3的值，进而计算各铰链补偿器的角位移幅值Θ1、Θ2、Θ3。

1.2 有限元仿真方法

通过有限元仿真确定管路中铰链补偿器的角位移时，需要按照管路的真实走向建立有限元模型。为了获得较精确的分析结果，建模时应考虑铰链补偿器的结构细节，建立包括接头、波纹管以及连接装置在内的精细化模型。完成网格划分并设置材料参数、约束条件、载荷及补偿边界条件后，通过静力学分析可获得整管的补偿变形情况。

分别提取管路变形后铰链补偿器两侧端面上的节点坐标，进行平面拟合后，可获得如下形式的空间平面方程：

式中l、m、n分别为拟合平面方程中参数x、y、z的系数。

根据式（3）可计算该平面的单位法向量n为

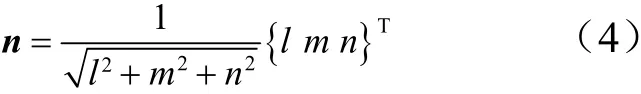
最后，铰链补偿器角位移幅值Θ可通过补偿器两侧端面的单位法向量为n1、n2计算得到：

1.3 静力试验方法

静力试验方法通过对真实管路产品施加补偿工况的温度、压力、位移等边界条件，使得管路发生补偿变形。在变形状态下，测量各铰链补偿器边缘距离的最大值Lmax、最小值Lmin，并按照下式计算补偿器的角位移：

式中Φ为铰链补偿器边缘直径。

2 三铰链管路补偿器角位移计算及测量

2.1 管路结构及补偿工况

某型号自生增压管路采用三铰链补偿方案，管路结构如图2所示。管路A、B、C、D段分别为平面弯管，通过铰链补偿器连接。管路组焊时各管段所在的平面并不重叠，因此管路整体呈现复杂三维走向。安装工况下，管路A0端固定、D0端沿法兰轴向进行预拉伸，拉伸量为80～120 mm。已知管路中铰链补偿器的最大设计变形量为10°，为了避免管路安装上箭后补偿器变形量过大，需要对拉伸补偿工况下补偿器角位移进行评估。

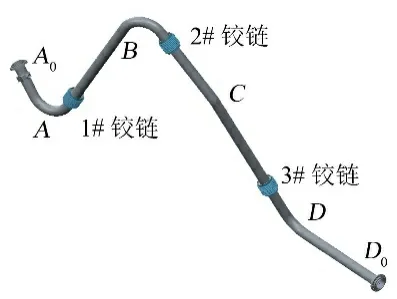
图2 某型号增压管路结构Fig.2 Structure of A Three-hinge Self-pressurization Pipe

2.2 理论计算

分别提取自生增压管路A0端、D0端法兰中心坐标、3个铰链补偿器中心坐标以及单位轴向矢量作为输入条件，分别设定D0端拉伸位移量为80 mm、100 mm、120 mm，使用自研理论计算方法对补偿器角位移进行计算分析。计算过程中涉及复杂的非线性方程求解，采用Levenberg-Maquardt方法，通过Matlab自编程序进行迭代计算，程序流程如图3所示。其中角位移分量的初始值为-1～1°范围内的非零随机角度值。Levenberg-Maquardt迭代过程中设置了用于调节迭代步长的参量λ：当某次迭代后残差减小时，接受迭代结果并将λ缩小10倍，以增加下一次迭代步长；否则，不接受迭代结果，并将λ增大10倍重新计算。当λ值很大时，说明残差已难以进一步减小，可认为迭代收敛。本文以λ大于1010为迭代收敛条件。

图3 自研理论方法计算流程Fig.3 Calculation Flowchart of the Self-developed Theoretical Method

2.3 有限元仿真

除理论计算外，使用有限元软件ABAQUS对图2中三铰链管路的拉伸变形进行了仿真分析。有限元建模时，将管路中各零件视为变形体，并赋予弹塑性材料属性，材料参数详见表1。导管、波纹管为薄壁结构，模型中将其简化为三维曲面，使用S4R单元进行网格划分；接头、法兰等零件为三维实体结构，使用C3D8R单元进行网格划分。图4为局部管路结构（铰链补偿器）的网格划分情况。同时，考虑管路真实装配情况，设置了各零件之间的连接关系：对于通过焊接相连的零件，模型中在对应位置设置了“Tie”约束；铰链补偿器内部为接头与连接装置的连接方式为铰接，模型中使用“Hinge”连接器模拟了上述铰接机构。

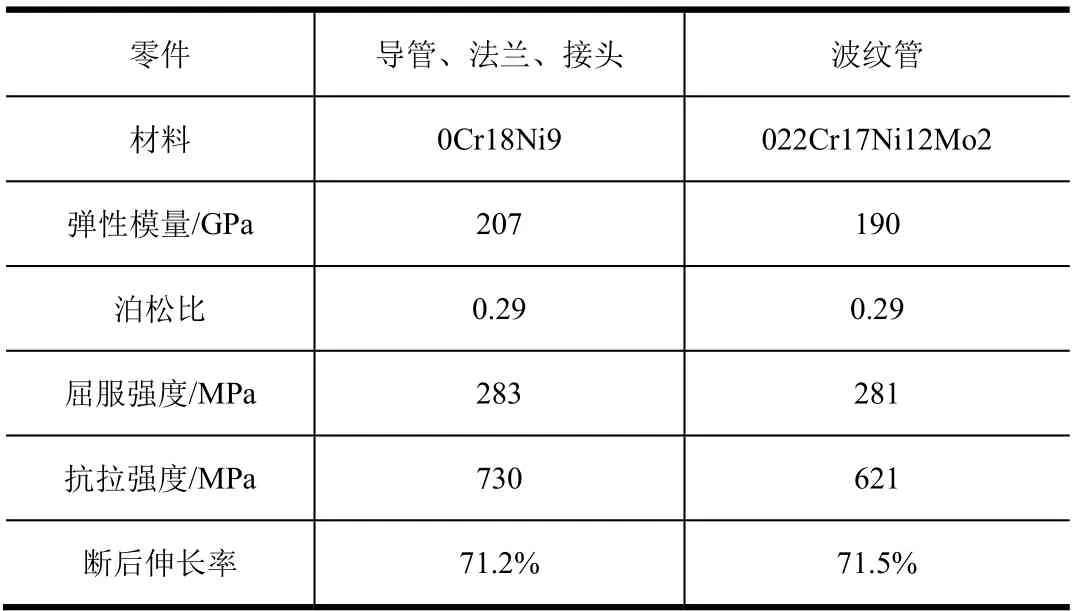
表1 三铰链管路有限元仿真材料参数Tab.1 Material Parameters Used in the FEM Analysis of the Three-hinge Pipe

图4 局部管路结构（铰链补偿器）的有限元模型Fig.4 Finite Element Model of the Local Pipe Structure (Hinged Expansion Joint)

分析中考虑常温环境条件、管路内部不充压的状态，设置管路A0端为固支边界，并在管路D0端施加位移边界条件。设置管路D0端拉伸位移分别为80 mm、100 mm、120 mm，分别使用“Static, General”分析步对管路补偿变形进行静力分析。

2.4 试验测量

为了研究拉伸补偿工况下真实管路产品中铰链补偿器的变形情况，本文制备了图1所示三铰链增压管的试验件，用于进行静力拉伸试验。管路试验装置如图5所示。管路安装时，将A0端固定于工装上，将D0端与横梁工装连接。试验过程中通过移动横梁工装，使管路D0端沿着图5中虚线箭头所示的位移方向分别移动80 mm、100 mm、120 mm，模拟管路预拉伸装配工况。每种拉伸状态下，分别使用刻度尺（最小刻度1 mm）沿着各铰链补偿器周向测量其边缘距离。读取各补偿器边缘距离的最大值Lmax和最小值Lmin后，结合补偿器边缘直径Φ计算其角位移值。本文试验中，自生增压管铰链补偿器边缘直径为79 mm。

图5 管路试验装置Fig.5 Experimental Setup of the Static Tensile Test

3 结果和讨论

3.1 理论计算结果

采用理论计算方法获得的自生增压管补偿变形情况如图6所示。图中给出了变形前、后三铰链管路铰链补偿器中心的连线。理论计算获得了不同拉伸量下3个铰链补偿器的角位移幅值，详见表2中“理论计算”。

图6 理论计算获得的自生增压管补偿变形Fig.6 Compensation Deformations of the Self-pressurization Pipe Obtained by Theoretical Calculation

表2 铰链补偿器角位移计算及测量结果Tab.2 The Calculated and Measured Angular Displacements of the Hinged Expansion Joints

3.2 有限元仿真结果

不同拉伸补偿量下，自生增压管的整管变形有限元仿真结果如图7所示。由图7可知，管路的补偿功能主要通过铰链补偿器的变形实现。提取3个铰链补偿器两端节点坐标，通过平面拟合及平面法向量夹角计算，可获得铰链补偿器的角位移，详见表2中“有限元仿真”。

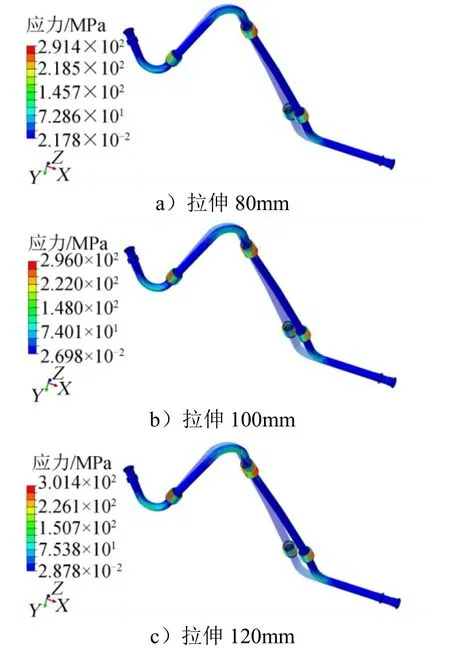
图7 有限元仿真获得的自生增压管补偿变形Fig.7 Compensation Deformations of the Self-pressurization Pipe Obtained by FEM Simulation

3.3 静力试验测量结果

在管路静力拉伸试验中，管路拉伸后铰链补偿器的变形情况如图8所示。按照上文所述方法，本文分别在管路拉伸80 mm、100 mm、120 mm后测量了3个铰链补偿器的最大和最小边缘距离，并根据式（6）计算了铰链补偿器的角位移。各拉伸工况下补偿器最大、最小边缘距离测量结果以及补偿器角位移试验结果见表2中“试验测量”。

图8 自生增压管静力拉伸试验时铰链补偿器的变形Fig.8 Deformation of a Hinged Expansion Joint in a Static Tensile Test of the Self-pressurization Pipe Specimen

3.4 测量结果分析和对比

3.4.1 一致性分析

通过3种方法对某型号三铰链自生增压管铰链补偿器进行角位移评估，结果一致表明：拉伸补偿工况下，2#铰链补偿器的角位移值明显高于1#、3#铰链补偿器。因此，该管路的最大补偿能力应根据2#铰链补偿器来确定。考虑铰链补偿器最大变形量为10°，确定自生增压管的最大安装预拉伸量为100 mm。

3.4.2 差异性分析

对比理论计算结果与有限元仿真结果可见：两种方法获得的铰链补偿器角位移一致性较好。以有限元结果为基准，计算两种方法角位移分析结果的最大相对误差为13.36%。该结果说明采用自研理论计算方法与有限元仿真方法均可完成三铰链管路补偿器角位移评估。造成分析结果差异的主要原因在于：a）理论计算方法假设管路中各管段均为刚体；而有限元分析结果（见图7）表明，管路通过补偿器变形进行边界补偿时，各管段折弯处通常为高应力区域，管段本体会发生变形，与上述刚体假设不符。b）理论方法计算变形能时将铰链补偿器视为线弹性元件；而实际上，铰链补偿器变形时波纹管会发生局部塑性变形，补偿器的整体性能并非理想线弹性，与线弹性假设不符。由于上述差异，理论计算结果的准确度通常不及有限元仿真结果。尽管如此，理论计算可通过编程实现批量、自动化处理，分析效率显著高于有限元仿真方法。

对比试验测量与理论计算、有限元仿真结果可见：不同拉伸补偿量下，3种方法获得的链补偿器角位移变化规律一致，但是数值存在差异。相同拉伸量下，1#铰链补偿器角位移的试验测量值偏大，而2#、3#铰链补偿器角位移的试验测量值偏小。分析造成上述偏差的主要原因为：理论计算、有限元仿真均未考虑铰链补偿器的刚度差异和内部摩擦力，但实际上不同铰链补偿器的刚度和顺滑程度通常存在差异。当管路中某一铰链补偿器刚度或摩擦力较小时，该补偿器在管路补偿变形是的角位移量将呈现偏大趋势。相对于理论计算和有限元分析方法，试验测量的优势在于能够避免模型简化引入的误差，最真实地反应管路产品的补偿特性；但是由于周期较长、成本较高，试验测量方法通常管路研制方案的最终验证时才使用。此外，在试验过程中对铰链补偿器最大、最小边缘距离位置的判断和测量无法做到绝对准确，也会引入一定的误差。

4 结 论

本文以某型号三铰链自生增压管为研究对象，分别采用自研理论计算方法、有限元仿真方法和静力试验方法对拉伸补偿工况下管路中3个铰链补偿器的变形情况进行评估。通过评估结果的一致性和差异性分析，给出该管路产品的补偿特性，同时对3种方法的优势和局限性进行了对比。研究结果可为三铰链管路设计时铰链补偿器变形量评估方法的选用提供参考。