最值函数算法下MMC电容电压优化平衡控制策略

马坤田，李 华，郝 悦，徐 宇

（1.内蒙古工业大学 电力学院，内蒙古 呼和浩特 010080；2.内蒙古电力科学研究院，内蒙古 呼和浩特 010080）

0 引 言

在化石能源日益枯竭的情况下，基于MMC拓扑的柔性直流输电技术（HVDC）为新能源的发展提供了一种灵活、可靠的技术方案，而对MMC合理的控制决定了其能否正常稳定运行，故显得尤为重要。

国内外许多学者对MMC的控制策略做了大量的研究与探索，而子模块电容电压的平衡控制更是其中的研究重点。文献[1]适用于MMC子模块数量较大时，针对换流器高额的开关频率以及巨大的运算量，引入基数法，减少排序次数，降低换流器的工作负担，缩减不必要的开关信号；文献[2]针对子模块电压的动态分布，通过可编程门列阵，完成电容电压的快速分段排序；文献[3]针对脉宽调制下的MMC换流器，通过各子模块开关信号的配合，使子模块开关频率能工作在基频条件下；文献[4]针对子模块开关频率问题，采用一种基准值比较的方法，将子模块分为两组进行投切，可以有效降低子模块开关频率；文献[5]针对MMC换流器中电容电压波动以及子模块高额开关频率的问题，按电压划分，将子模块分到不同的组内进行处理，针对工程问题，采用实时仿真及编程完成子模块的均压控制。

由于工程中MMC通常含有上百个子模块，如此众多的子模块中的IGBT的数量要更多，IGBT的频繁投切导致其损耗巨大、寿命缩短，因此对于如何降损，降低投切频率的研究显得尤为重要。本文提出一种针对前后周期上、下桥臂子模块投切数量的变化，只对变化量进行处理，减少了子模块当前状态的变化率，进而减少投切频率。

1 MMC的数学模型

图1 给出了MMC及子模块SM结构，三相模块化多电平换流器的每相包含上、下两个桥臂。相电流i C以及子模块电压u C、电流iSM的关系可以表示为[6]：

式中：S为开关函数，S=1为开通状态，S=0为关断状态。

图1 MMC及SM拓扑结构

桥臂的电压公式为：

式中：u p i和u n i为上、下桥臂电压；S pi j，u pi j为上桥臂子模块开关状态和电容电压；S ni j，u ni j为下桥臂子模块开关状态和电容电压[6]，即各桥臂电压是由所有投入状态的子模块电容电压共同支撑[6]。

在不考虑桥臂等效电阻和电抗的情况下，相电压为上下桥臂电压之和，即：

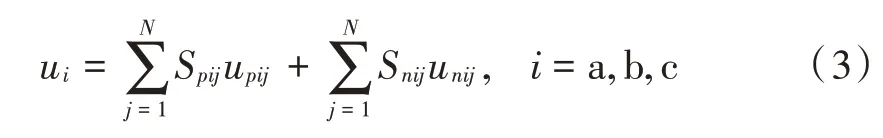
2 调制方式

本文中采用的最近电平NLM调制是MMC换流器中常用的调制方式，属于低频调制，它通常与排序算法配合使用，且NLM调制尤其适用于多电平的换流器，与高频类调制方式相比，在多电平换流器中，它的运算负担要小，工作量相对较少，交流侧的谐波含量较低，能输出较好的正弦波形。最近电平调制流程如图2所示。

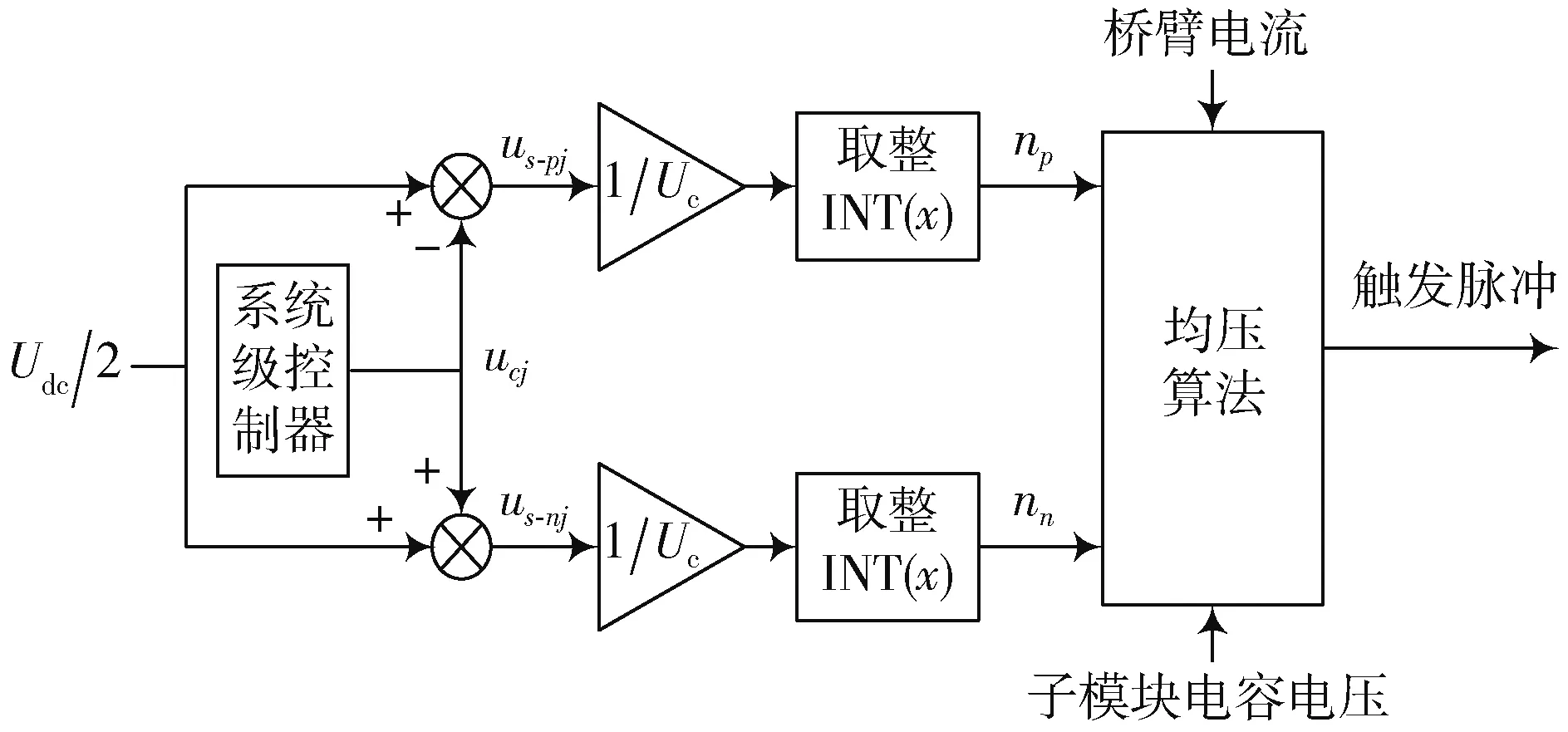
图2 最近电平调制流程

3 最值函数算法下的电容电压平衡控制

现行的子模块电容电压平衡控制策略虽然在子模块的电容电压平衡方面也能实现有效控制，但高额的开关频率一直是难以解决的问题。由于其在每一周期内对子模块的电容电压进行排序后都会重新投切大量子模块，由此造成高额的投切频率，开关损耗随之增加。因此，作为子模块投切原则的核心，电容电压平衡控制策略的优化显得尤为重要。

本文在现行排序算法的基础上，采用基于最值函数的电容电压平衡控制算法，即只针对电容电压最大和最小的子模块更改其投切状态。

算法核心内容包括：

1）为了使每个控制周期要改变投切状态的子模块尽可能地少，需紧随n p（或n n）单位攀爬或下降，且开关事件遍历MMC的每个电平。为了满足上述要求，控制器的采样周期必须低于相邻两个开关事件之间的最短周期，需遵循式（4）。式中：ω为电网角频率；TS为采样周期；N愈大，Δt愈小。

2）根据桥臂子模块数投切变化量Δn的不同，可以将子模块的投切分为三种工作模式，具体如下：

工作模式一：各桥臂子模块数投切变化量Δn>0时，通过最值函数挑选其中的Δn个子模块，桥臂电流为正（负），子模块充电（放电），在旁路的子模块中挑选电容电压最小（最大）的Δn个进行投入。

工作模式二：投入子模块数Δn<0，桥臂电流为正（负），子模块充电（放电），在已投入的子模块中挑选电容电压最大（最小）的Δn个切除。

工作模式三：投入子模块数不变时，即Δn=0，桥臂电流为正（负），子模块充电（放电），当处于投入状态的电容电压最大（最小）的子模块，与处于切除状态的电容电压最小（最大）的子模块，两者之间电压差绝对值超出设定的阈值时，对其进行调换，否则，保持原状态。

基于最值函数的电容电压平衡控制算法流程图如图3所示。其中为当前周期需处于投入状态的子模块数为上一周期需处于投入状态的子模块数为桥臂电流为处于投入状态的电容电压最大（最小）的子模块，与处于切除状态的电容电压最小（最大）的子模块之间电压差绝对值；ΔUref为判定阈值。

图3 基于最值函数算法的电容电压平衡算法流程

4 仿真分析

在PSCAD/EMTDC中搭建双端201电平的MMC⁃HVDC输电模型，如图4所示。

图4 MMC⁃HVDC系统结构图

双端MMC⁃HVDC系统仿真参数如表1所示。

为了验证最值函数下电容电压平衡控制的有效性，分别对现行排序算法的电容电压平衡控制及所提算法进行仿真验证。仿真结果如图5~图8所示。

图中子模块投切状态S=1为开通状态，S=0为关断状态，通过仿真图5~图8两种算法下子模块a的触发频率对比可以看出，现行排序算法下子模块a在0.08 s内投切次数为88次，最值函数电容电压平衡控制下子模块a在0.08 s内投切次数为21次，平均触发频率由1 100 Hz降低到262.5 Hz（见表2），有效降低了开关频率，进而降低了开关损耗。但由于子模块所储存的能量与其电压平方成正比，因此本文算法的特性导致电容电压最大的子模块电容会有偏差，但偏差量较低，对换流器的整体电压影响并不大。

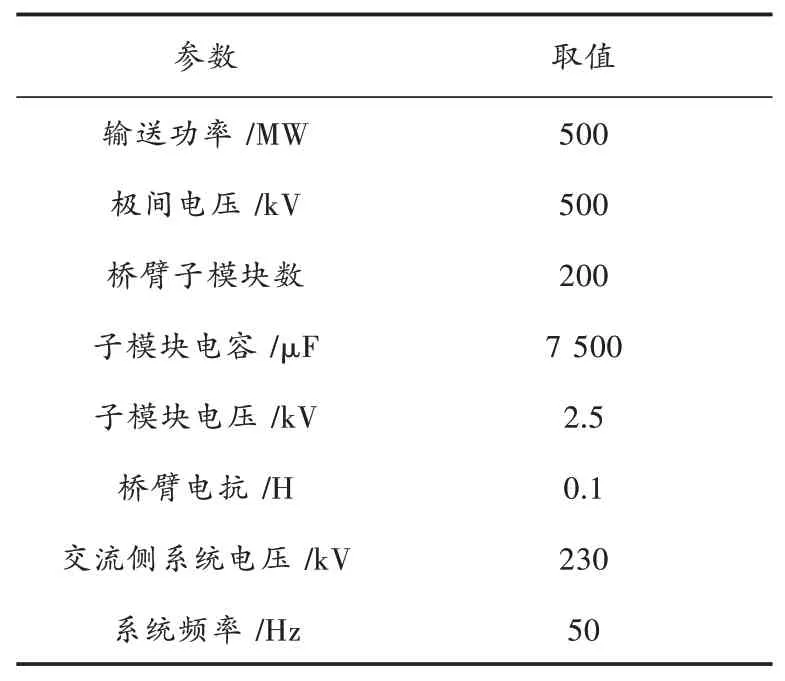
表1 双端MMC⁃HVDC系统仿真参数

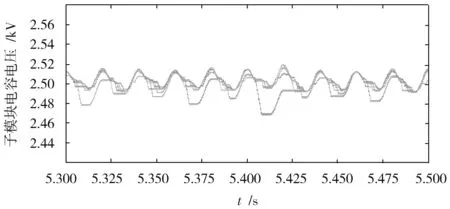
图5 现行排序算法下子模块电容电压

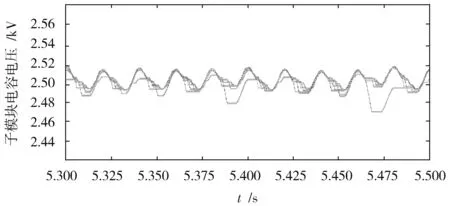
图6 最值函数算法下子模块电容电压

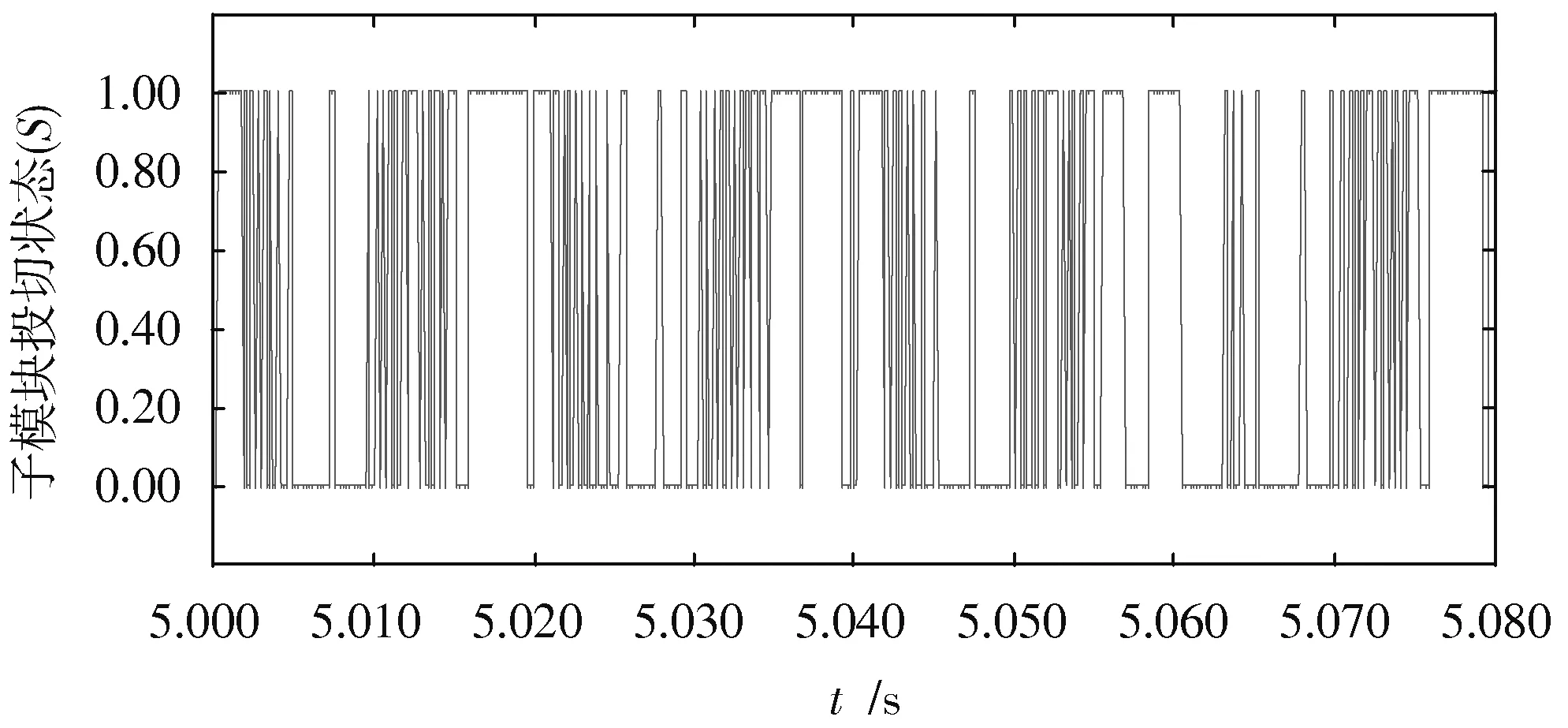
图7 现行排序算法下子模块投切频率

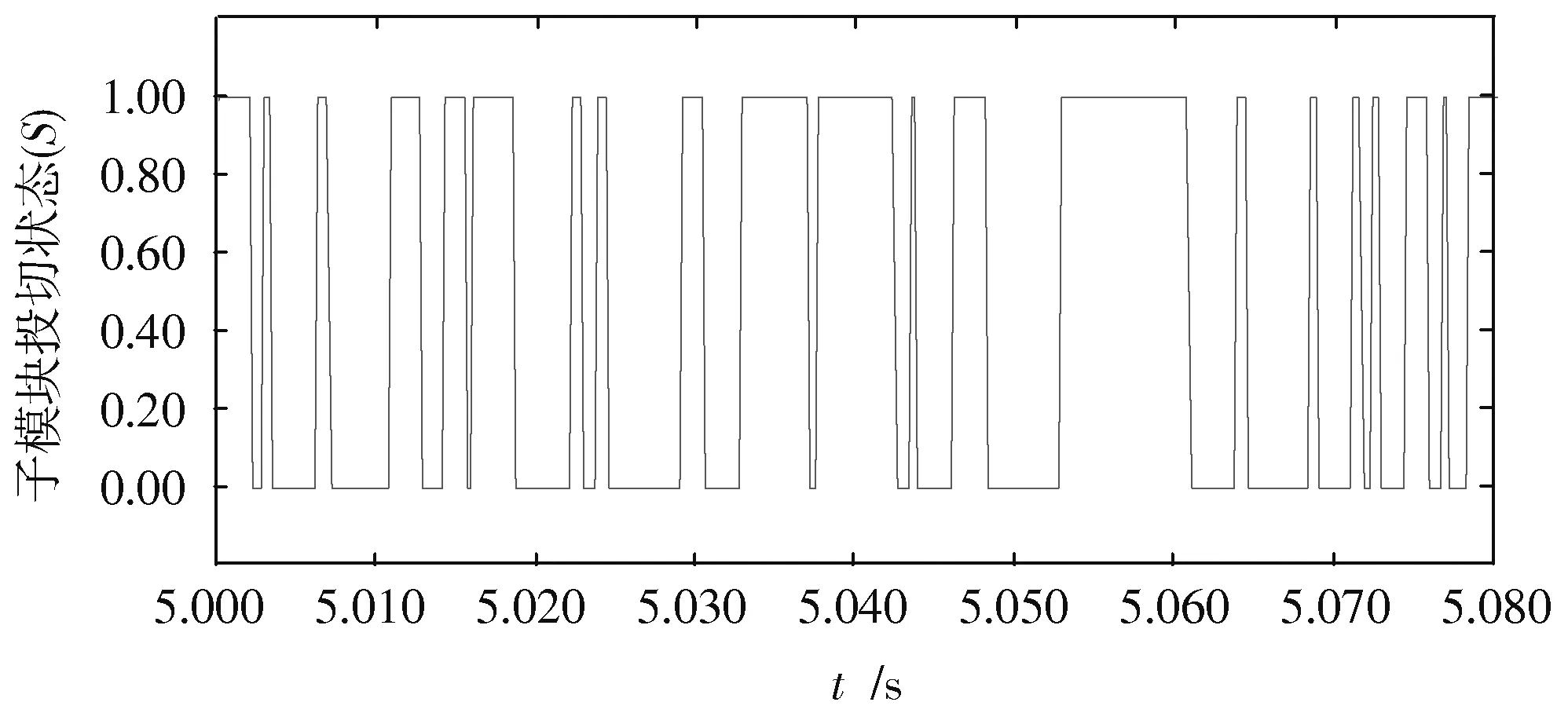
图8 最值函数算法下子模块投切频率

5 结 语

本文在MMC最近电平调制中上、下桥臂子模块投切数量逐步变化特性的基础上，针对前后周期上、下桥臂子模块投切数量的变化量Δn，在重新排序后，只选取子模块中电容电压最大（最小）的Δn个进行处理，将工作模式分为三种，在Δn>0，Δn<0，Δn=0三种情况下，根据桥臂电流的方向，只对选定的Δn个电容电压最大或最小的子模块进行投切状态的改变，这种投切方式可以有效减少现行排序类算法下子模块投切状态的变化率，进而有效减少投切频率。

最值函数算法下电容电压平衡控制策略的优势：最值函数计算耗时比现行排序类算法短；与现行排序算法相比，每个控制周期基本上只改变极少量子模块的投切状态，保证极低的IGBT管开关频率，为现行的MMC工程中普遍使用的排序算法下的电容均压控制提供了一种新的优化策略，可以延长MMC系统中IGBT管的使用寿命，减少投资。