带有丢包和时变延迟的事件触发故障滤波检测

黄玥程，童东兵

(上海工程技术大学 电子电气工程学院,上海 201620)

在一般的网络控制系统(Networked Control Systems，NCSs)中，传感器、控制器以及控制对象通过公用的网络媒介进行连接，从而组成一个完整的控制系统[1]。然而，在NCSs的运行过程中，当数据通过公共网络进行数据传输时，将产生网络诱导延迟。通过文献[2～3]可知，网络诱导延迟是由公用的有限网络带宽引起的。网络诱导延迟影响系统的性能，甚至导致系统不稳定。在实际运行过程中，NCSs不可避免地会产生故障。根据文献[4～5]，关于NCSs的故障检测和容错控制已经取得了一定的成果：文献[4]讨论了NCSs在有限频域中的故障检测问题；文献[5]介绍了变采样周期法处理NCSs故障检测滤波器(Fault Detection Filter，FDF)的方法。值得指出的是，文献[6]忽略了网络诱导延迟的问题；文献[7]忽略了网络丢包问题，这些问题在NCSs的故障诊断过程中有着重要的影响。对于受传感器故障或执行器故障影响的连续时间NCSs，网络诱导延迟和信号丢失将给基于NCSs和FDF的建模及控制器协调设计带来较大困难。

在研究故障检测滤波的过程中，NCSs中的采样状态或测量输出可能会因为网络波动或者其它故障导致出现偏差，而这些误差数据是不值得被获取的。在这种情况下，将不必要的采样数据释放到通信网络中是对网络资源的浪费。因此，为了解决这个问题，采用事件触发机制[8]来过滤不必要的数据。根据文献[9]，事件触发机制的引入使得系统仅当触发信号满足设定机制时才能进行下一步工作，不满足事件触发机制的信号将会被丢弃。然而，在对数据包丢失的研究过程中，因为事件触发机制而被有目的丢包和系统故障或拥堵造成的数据包丢失容易混淆[10]。文献[11]描述了在理论基础上的最大允许丢包数，并且表示在事件触发机制中，丢包与事件触发机制的协同设计不容易进行理论计算。因此，研究包含丢包的事件触发NCSs的故障滤波检测有着重要的理论意义。

本文研究了基于事件触发的FDF和控制器协同设计。同时，考虑了网络诱导时延、丢包和偏置传感器故障对连续时间网络控制系统的影响。 根据文献[12]，本文采用了随机Bernoulli分布函数建模数据包丢失，基于此提出了丢包和时变时滞的事件触发机制。结合事件触发机制和FDF，建立了一种新的网络控制系统闭环模型。在此基础上，本文使用互斥分布和Jensen’s不等式，提出了一种基于FDF和事件触发机制的系统渐近稳定设计方案。

1 问题描述

图1是F-18战机的多输入多输出系统，其中βc、β、pc、p分别表示侧滑命令、侧滑角度、滚速命令以及车辆滚动率。通过文献[13]可知，F-18战机的故障检测系统是一个以无线通讯为通讯网络的NCSs。

图1 F-18战机多输入多输出控制系统

图2提出了一种基于NCSs的事件触发故障检测系统结构。该结构利用事件触发来确定是否将采样的测量输出释放到FDF，并存储最近发布的测量输出。

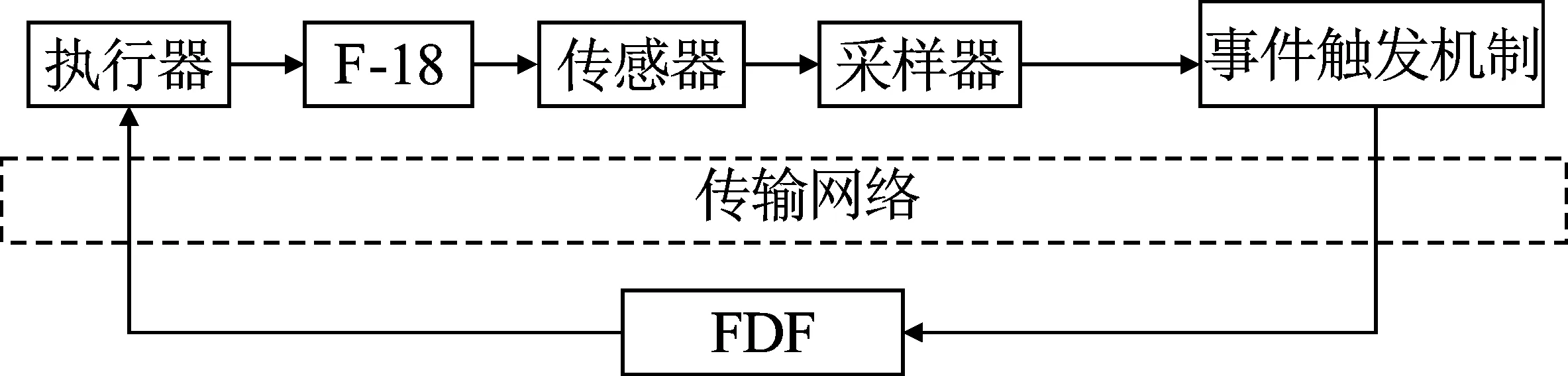
图2 基于事件触发机制的NCSs故障检测构造图

基于文献[12]，F-18的动力学方程可以表示为

(1)

式中，x(t) ∈Rn是状态向量；u(t) ∈Rq是控制输入向量；y(t) ∈Rm是测量输出；ω(t) ∈Rp是外部扰动。

根据式(1)，采用如下的FDF来生成残差信号

(2)

本文的事件触发机制被定义如下

(3)

其中，i∈Z+；h∈R+；tkh是触发时刻，k∈Z+；y(tkh)是触发时刻的系统输出；W是正定矩阵；σ∈[0,1)是一个给定的标量。

在时间区域t∈[tkh+τk,tk+1h+τk+1)，假设τm≤τk≤τM且τm≥0，定义如式(4)。

(4)

为了进一步分析事件触发机制，定义两个分段函数。其中时变时滞τ(t)被定义为

(5)

触发输出误差ek(t)被定义为式(6)。

(6)

在式(5)与式(6)的基础上，事件触发机制(3)可以被重新写为

(7)

根据文献[13]，当传感器发生故障时，由于无法确定故障原因和位置，因此定义

yfi(t)=y(t)+fiξi,i=0,1…,l

(8)

其中，i表示了第i种故障原因。当i= 0时，则传感器中没有故障。ξi= diag[ξi1,ξi2,…,ξim]T，矩阵ξij表示了第j个传感器的偏离值，j=0,1,…,m。

fi是一个对角矩阵，其矩阵形式如下

fi=diag{fi1,fi2,…,fim}

(9)

其中，fij=1或者fij=0。fij=0表示在第j个传感器中没有故障；fij=1则表示在j个传感器中存在故障。

在时间区域t∈[tkh+τk,tk+1h+τk+1)中，综合考虑事件触发机制的触发输出、网络丢包、以及时变时滞的问题，FDF的测量输出定义如式(10)。

yfi(t)=δ(t)(Cx(tkh)+fiξi)

(10)

(11)

(12)

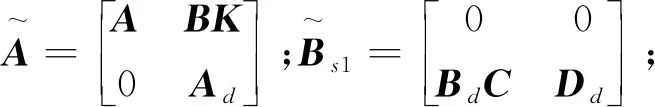
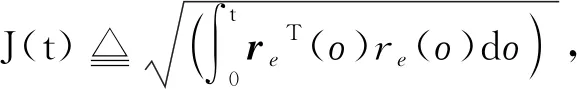
今天我们在这里举办干部人事工作培训班，主要任务是深入学习贯彻全国、全省组织工作会议以及深化机构改革精神，深化落实干部人事工作新精神新要求新任务，开展干部人事工作业务培训，分析部署当前和今后一个时期干部人事重点工作。厅人事处作了干部人事工作业务辅导，各市局交流了 2019 年工作思路及对省厅干部人事工作的意见建议，大家讲得都很好，我完全赞同。希望会后大家严格贯彻执行干部人事制度，认真谋划2019 年工作思路和重点工作。借此机会，我讲三点意见。

2 结果

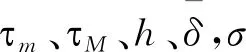
系统(12)是渐进稳定的。

证明考虑如下的李雅普诺夫函数

V(t,ζ)=V1(t,ζ)+V2(t,ζ)+V3(t,ζ)

(13)

其中，V1(t,ζ)、V2(t,ζ)、V3(t,ζ)如式(14)所示。

(14)

在时间区域t∈[tkh+τk,tk+1h+τk+1)内，对式(14)中的李雅普诺夫函数沿着式(12)的轨迹对时间进行求导。

(15)

由于丢包函数δ(t)满足Bernoulli分布，因此对(15)求期望得

(16)

其中

Θ1=

ζT(t)Qζ(t)-ζT(t-τm)Qζ(t-τm)=TΘ2，

(17)

(18)

因此，基于式(16)～式(18)，可以得到

(19)

其中，Θ=Θ1+Θ2+Θ3.1+Θ3.2，

通过式(19)，故障检测系统即式(12)被证明在时间区域t∈[tkh+τk,tk+1h+τk+1)是渐进稳定的。

3 数值仿真

本文在分别考虑了静态故障以及动态故障的情况下，证明了基于事件触发的FDF能够有效地检测到故障，并且事件触发机制在NCSs中能够节约网络计算资源。

考虑如下参数

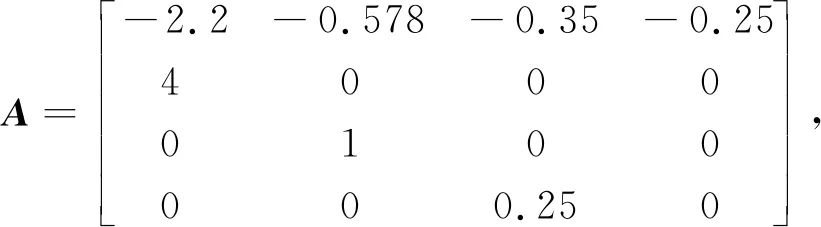
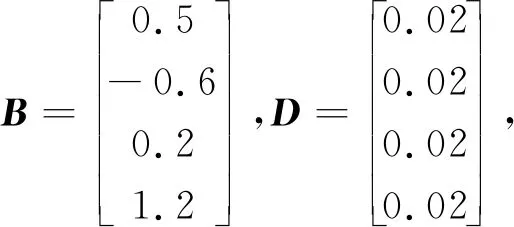
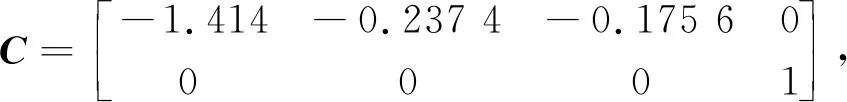
Ad=0.2，Bd=0.8，Dd=0.5，Cd=0.2，κ=1。

使用MATLAB求解LMI得

W=3.174。

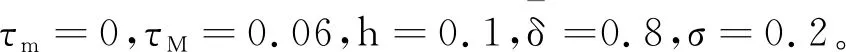
(20)

从图3中可以看出，当系统无故障时，系统的残差函数曲线一直保持在残差阈值之下。当系统检测到残差函数J(3)>Jth时，FDF在很短的时间内检测到系统发生故障。图4可以明显看出在10 s内系统触发了42次。也就是说，在h= 0.1的条件下，系统的触发概率为42%。

图3 故障f1控制下的残差函数

图4 故障f1控制下的触发间隔

当系统发生如下动态变化的故障时

(21)

在所有条件不变的情况下，故障f2的曲线图、故障f2控制下的残差函数以及事件触发时间间隔分别如图5和图6所示。

从图5中可以看出，当系统无故障时，系统的残差函数曲线无限接近残差阈值Jth。当系统检测到残差函数J(4)>Jth时，FDF检测到系统发生故障。图6可以看出在10 s内，系统触发了43次。同样的，在h=0.1的条件下，系统的触发概率为43%。 这也证实了事件触发FDF可以降低网络负载压力。

图5 系统f2控制下的残差函数

图6 系统f2控制下的触发间隔

4 结束语

本文研究了网络诱导时延、丢包和偏置传感器故障的事件触发FDF的问题。针对具有时变时滞和丢包的网络化控制系统，提出了可以节省网络资源的事件触发机制，从而建立了一种新的网络控制系统闭环模型。通过使用Jensen’s不等式，推证出基于事件触发机制的FDF渐近稳定。在此基础上，本文提出了事件触发FDF与控制器协调设计方案。仿真结果验证了设计方案的有效性。