基于博弈论的互联微电网多主体协同优化配置

梁龙基，张 靖，何 宇，曾希皙，陈朝宽

(贵州大学 电气工程学院,贵州 贵阳 550025)

随着分布式发电技术的发展及成本的不断下降，作为可再生能源就地平衡解决方案的微电网必将大量出现在用户侧与配电网端[1]。在临近范围内，新建或改造而成的微电网可相互连接，实现电能的互通互济，构成互联微电网[2-3]。在分属不同投资运营主体的微电网互通互济的情况下，因地制宜对其进行规划建设已成为需要首先解决的问题。

近年来，国内外专家学者从不同角度对微电网或多微电网优化配置进行了一系列研究。文献[4]考虑了小水电的有功出力对微电网分布式电源容量的配置影响。文献[5]提出了一种以提高配电网侧的供电可靠性为目标的多阶段决策微电网规划方法，并采用动态和声算法求解微电网中分布式电源的配置容量。文献[6～7]对直流微电网与交流微电网规划的异同进行对比分析。文献[8]提出了一种考虑微电网孤岛情况下的一次调频备用容量配置方法，建立模糊随机机会规划模型，从而得到不同置信度下微网中各分布式电源容量大小。文献[9～10]均以考虑并网型微电网设计经济效益为切入点，建立微电网全寿命周期优化模型，讨论了政策激励对实际微电网建设收益的影响。

在目前的研究中，大多是为了追求微电网规划导则中某些指标最优，或针对单一微电网解决其分布式电源配置问题。然而，随着区域性能源交易的开展，微电网作为市场参与者在可以进行电能购售的情况下，多微电网相互之间的影响作用将逐渐凸显。因此，将多微电网规划建设纳入博弈的框架下讨论显得很有必要[11]。文献[2]结合实际示范工程的设计方案，提出了多微电网的一般规划设计流程，但对微电网群运营层面因素考虑不全面，尤其是未考虑储能电池的调用成本对多微电网收益的影响。文献[12]分析了多微电网及其子微电网在不同运行工况下储能容量的配置，但储能电池的调用仅在微电网缺额时作为补充，未考虑风光发电富余时存储电能的作用。文献[13]为欧盟可再生能源及微电网开发框架计划支持下的对多微电网配置规划分析，重点讨论了不同国家微电网项目需求的技术解决方案，但并未给出求解多微电网具体的分布式电源容量配置模型。文献[14]将风力发电、光伏发电与储能设备发电三方作为博弈参与者，分属不同投资主体进行博弈分析，提出非合作/合作博弈模式，求得不同分布式电源的容量优化配置方案。

本文利用博弈论解决不同决策主体行为相互影响的问题，提出了典型风-光-储互联微电网全寿命周期(Life Cycle Cost，LCC)分布式电源容量非合作博弈模型，各参与者的费用函数同时考虑了购售电收益、可再生能源消纳收益及建设运维成本。在进行互联微电网规划的决策时，本文将储能电池调用成本有机结合到规划建设建模中。本研究在互联微电网电能的互通互济影响博弈参与者收益的模式下，通过博弈联动优化使博弈各参与方的分布式发电单元配置达到均衡，实现了互联微电网不同投资方的收益最优。

1 微电网中分布式电源出力及负荷模型

针对微电网分布式发电单元容量的优化配置，建立了包括风力发电、光伏发电、储能充放电的出力模型与微电网负荷模型。

1.1 风机出力概率模型

风速的大小具有随机性，双参数威布尔分布的概率密度函数能够精确描述风速变化规律

(1)

式中，v为风速；k为形状参数，反映风速分布的特点；c为尺度参数，反映的是该地区平均风速的大小。风机的有功输出PWT可用下式表示

(2)

式中，PWT_N为风机的额定功率；vci为切入风速；vN为额定风速；vco为切出风速。

1.2 光伏出力概率模型

光伏发电的有功出力PPV可以近似用概率密度函数贝塔(Beta)分布进行表示

(3)

式中，PPV_MAX为光伏方阵发电最大出力；Γ(·)为Gamma函数；α、β为Beta分布的形状参数。

1.3 储能电池模型

储能电池具有在满足一定条件下的可调节性，其充放电满足以下关系，储能电池充电时

S(t)=S(t-1)(1-δ)+Pc(t)ηc

(4)

储能电池放电时

S(t)=S(t-1)(1-δ)-Pd(t)ηd

(5)

式中，S(t)为储能电池t时刻的电量；S(t-1)为储能电池t-1时刻电量；Pc(t)与Pd(t)分别为储能电池在t时刻的充电功率与放电功率；ηc与ηd分别是储能电池的充电和放电效率；δ为蓄电池的自放电率。

1.4 负荷概率模型

微电网负荷有功的概率密度函数，如下所示

(6)

式中，PL为微电网内电力用户负荷值；μP为微电网内负荷值的均值；σP为微电网内负荷值的方差。

2 微电网收益-成本博弈模型

微电网具有统一的运营主体，主要负责其优化协调运行[15]。在微电网环境收益方面，有关部门制定了可再生能源电力消纳责任权重的相关机制。该机制可以起到发现可再生能源真实价格与体现可再生能源外部特性的货币价值的作用，影响分布式发电的配置规划[16]。由于区域范围内多微电网存在电能互通互济，因此增加分布式发电单元容量可以获得更多收益。若通过其他微电网的供能满足自身用电需求，则可比增加自身分布式发电单元容量供电获得更多收益。因此，不同微电网主体之间存在容量配置的博弈关系。本文将储能电池的调用成本视为影响微电网收益的重要因素，建立了计及储能调用成本的互联微电网配置博弈模型。

2.1 储能电池在不同运营情形的调用依据

储能电池的使用寿命一般由其实际运行时的循环次数决定。储能电池的荷电状态值(State of Charge，SOC)是影响储能电池使用寿命的最主要因素[17-19]。储能电池在充放相同电量的情况下，荷电状态较低时对电池的损耗较大，荷电状态较高时对电池的损耗较小。储能电池的寿命损耗权重与荷电状态的关系，如图1所示[20]。

图1 储能电池荷电状态因素的寿命损耗权重

荷电状态的电池折损度电成本，如式(7)所示

Cp=Ra(SOC(t))Ceg

(7)

式中，Cp为当前荷电状态下调用储能的成本值；Ra(SOC(t))为t时刻电池寿命损耗权重；SOC(t)为t时刻储能电池的荷电状态。

Ceg为电池折损的度电成本[21]

(8)

式中，Tcalendar为储能电池的日历寿命；LE为储能电池全寿命周期总充放电量；CAPV为电池投资与运维成本的等年值。

采用资本回报系数修正后的投资成本应用于度电成本计算式中

(9)

式中，Cinv为储能一次投资成本；Com为年运维成本；r为贴现率。

关于储能电池的全寿命周期总充放电量LE，可由确定循环放电深度后的电池循环寿命得到。一般厂商会根据其化学性质通过幂函数拟合得到电池的循环寿命[22]，如式(10)所示。

Nlife=N0(dcycle)-kp

(10)

式中，Nlife为储能电池达到寿命终点时的循环次数；N0为储能电池以100%放电深度充放电时的循环次数；dcycle为电池储能充放电循环的放电深度；kp为拟合得到的常数。N0与kp的值对于不同类型的储能电池有不同的取值，通常厂商会提供相关参数。LE则由20%与80%放电深度放电下的充放电量总平均值得到。

2.2 计及储能电池调用成本的购售电收益

微电网运营主体购售电收益主要来自两方面：一方面是满足其运营区域内的电力用户用电需求；另一方面是满足区域市场其他主体的购电需求。微电网i的购售电收益fs_i，可表示如下

fs_i=fdeal_i+ftrans_i+fg_i

(11)

式中，fdeal_i为微电网运营主体通过对微电网内部分布式发电单元出力进行控制从而满足微电网内部负荷的收益；ftrans_i为互联微电网之间通过电能互通互济的购售电收益；fg_i为微电网与配电网侧的电能交互收益。

在考虑储能电池的调用成本、风力发电与光伏发电有功出力后，微电网的fdeal_i收益可用两种情况分别表示：

(1)风力发电与光伏发电有功出力满足负荷需求

fdeal_i=PRdealPL_i(t)

(12)

式中，PRdeal为微电网投资运营主体与微电网内用户协商电价；PL_i(t)为t时刻微电网i的负荷；

(2)风力发电与光伏发电有功出力不满足负荷需求，而储能电池存在参与出力的可能，储能电池动作与否则需要进行比较判断

fdeal_i=PRdeal(PWT_i(t)NWT_i+PPV_i(t)NPV_i+

PBAT_i(t)NBAT_i)

(13)

式中，PWT_i(t)、PPV_i(t)与PBAT_i(t)分别为微电网i的单台风机、光伏面板与储能电池的有功出力。当储能电池为充电状态时，PBAT_i(t)值为Pc(t)，当储能电池放电时PBAT_i(t)，值为Pd(t)；NWT_i、NPV_i与NBAT_i分别为微电网i的分布式发电电源的配置数量。

将每个微电网相互间送出或购入的电量由运营流程判断得出，其具体流程如图2所示。

图2 计及储能调用成本的互联微电网运营流程图

多个微电网互联互通电量收益可表示为

ftrans_i=PRgqΔEex_i(t)

(14)

式中，PRgq为互联微电网之间电量交换单价；ΔEex_i(t)为微电网i参与微电网之间电能交换的t时刻电量。

当微电网自身供能及临近微电网的电能互供无法使微电网内功率达到平衡时，微电网主体需同配电网额外购售电。其收益构成如下式所示。

fg_i=PRgΔEsur_i(t)

(15)

式中，PRg为微电网与配电网侧电能交换价格；ΔEsur_i(t)为t时刻微电网i与配电网的交换电量。

2.3 可再生能源消纳权重收益

由于微电网主体在市场中为购售电运营主体，其必须承担可再生能源消纳的义务。当市场主体不满足可再生能源消纳权重的比例时，则受到相应“惩罚”；当市场主体超额完成消纳比例时，则有额外激励。参考《可再生能源电力消纳责任权重确定和消纳量核算方法》，对微电网其收益用下式表示

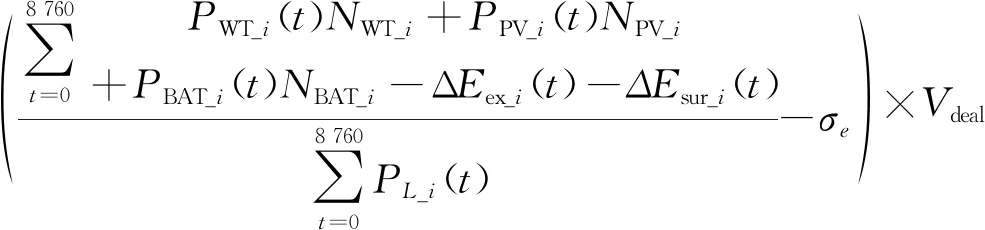
(16)

式中，fe_i为微电网i消纳可再生能源收益。当微电网可再生能源消纳不足设定比例时为负，超额实现消纳比例时为正；σe为可再生能源消纳权重；Vdeal为每提高或降低一个百分点的消纳权重所对应的激励。

2.4 微电网LCC成本

在对微电网建设项目成本评价时，不仅考虑微电网建设初期的一次性投入成本，也要考虑工程全寿命周期内的支持成本，并将规划年的成本归算到基准年。其总成本可表示为

Ct_i=Cinv_i+Com_i+Ccd_i

(17)

式中，Ct_i为微电网i的投运总成本的等年值；Cinv_i为该微电网总初始投资费用；Com_i为该微电网年运维费用；Ccd_i为该微电网废弃成本。

微电网的初始投资费用，可表示为

(18)

式中，IWT、IPV和IBAT分别为风力发电、光伏发电和储能电池的设备单价；R1为微电网一次网架成本与分布式电源投资建设成本的比值；R2为微电网二次设备成本与分布式电源投资建设成本的比值；l为工程寿命周期。

微电网的年运维费用，可表示为

(19)

式中，MWT、MPV和MBAT为微电网分布式电源容量的单位年运维费用；EWT_i、EPV_i与EBAT_i分别为微电网i的对应分布式电源的容量、分布式发电单元配置数量与各自额定容量乘积。

微电网的废弃成本，可表示为

Ccd_i=Y-S_i

(20)

式中，Y为报废处理成本，其值为一常数；S_i为微电网i的残值，其值可通过如下计算式计算得到

S_i=Cinv_ib

(21)

式中，b为残值率。

2.5 约束条件

(1)等式约束条件。在运营过程中，每个微电网在t用电时刻的供需要达到功率平衡，其约束表示为

PWT_i(t)NWT_i+PPV_i(t)NPV_i+PBAT_i(t)NBAT_i+ΔEex_i(t)+ΔEsur_i(t)-PL_i(t)=0

(22)

(2)不等式约束条件。决策变量约束，风机台数、光伏面板数和并联储能电池数为优化决策变量，可表示为

(23)

式中，NWT_MAX、NPV_MAX与NBAT_MAX分别为微电网决策变量的上限值。上限值可根据实际的投资预算与分布式发电单元设备适用场地的大小进行调整设置。

微电网分布式电源运行约束，某时刻的单台风力发电与储能电池的有功出力应不大于其额定有功出力，而光伏发电单元出力则不可大于该段时刻最大出力，如下

(24)

式中，PWT_N与PBAT_N分别为分布式发电单元额定功率。此外，储能电池还存在某时刻的荷电状态约束

SOCmin≤SOC(t)≤SOCmax

(25)

式中，SOCmin与SOCmax分别为储能电池荷电状态的下限值和上限值。

互联微电网运行约束，互联微电网之间的电量传输受到联网输电线路的最大传输能力限制，表示为

ΔEex_i(t)≤Eex_MAX

(26)

式中，Eex_MAX为微电网间的最大传输功率。

微电网与配电网连接点功率约束为

ΔEsur_i(t)≤Esur_MAX

(27)

式中，Esur_MAX为微电网与配电网间最大传输功率。

2.6 目标函数

综上所述，参与博弈各方的微电网支付函数可以表示为式(28)。

MaxF_i=fs_i+fe_i-Ct_i

(28)

下文将讨论如何对支付函数进行博弈求解。

3 博弈模型的均衡求解

3.1 不同主体互联微电网配置的均衡解

(29)

即当非i参与者在其他参与者选择最优配置的策略下均使得自身收益最大化时，博弈达到均衡。

3.2 基于整数粒子群算法的博弈模型求解

为解决上述i个参与者的微电网规划建设博弈问题，本文采用整数规划粒子群算法(Particle Swarm Optimization，PSO)求解纳什均衡点[23]，其具体算法步骤如下：

步骤1博弈模型初始化。主要包括风、光和负荷数据输入，初始化电价参数PRdeal、PRgq和PRg；分布式发电单元配置单价IWT、IPV和IBAT；单位运维成本MWT、MPV和MBAT与决策精度范围ε；

步骤2设定决策变量初始值。初始值应在决策变量的策略空间选取，本文以博弈前各参与者的分布式发电单元数量N0_i=(N0WT_i,N0PV_i,N0BAT_i)作为决策变量初始值；

步骤3各博弈参与者独立优化决策过程。在优化各个微电网第j轮的微电源配置Nj_i时，可根据上一轮优化的分布式发电单元配置，通过整数粒子群算法优化得到

(30)

步骤4判断博弈是否到达纳什均衡点。在优化过程中，若分属不同主体的微电网在优化前后的分布式发电单元配置数量大小之差均在设定的精度范围ε内，即优化决策满足式(31)，则博弈达到纳什均衡。参与者i在现存条件下，任一参与者均不能通过独立改变策略而获得更多收益，即等年值收益达到纳什均衡意义下的最大值。纳什均衡解，如式(32)所示。

(31)

(32)

若找到纳什均衡点，则进入步骤5；若未达到纳什均衡，则根据整数粒子群算法更新决策，返回步骤3继续优化决策。

4 算例分析

本文采用上述模型与方法对3个不同主体的微电网进行优化配置。3个微电网的负荷均值分别为100 kW、3 000 kW和300 kW，方差均为1。算例仿真以1年为计算周期，共分为8 760个步长，每个步长为1 h。双参数威布尔分布与贝塔分布中的形状参数由历史数据拟合得到。将由各个分布函数抽样得到的数据带入模型计算各博弈参与方的收益-成本函数值。微电网设备参数及模型相关参数如表1和表2所示。

表1 设备参数

表2 参数设置

4.1 博弈前后收益-成本分析

将没有电能传输且彼此分布式电源配置决策不会对同区域内其他微电网产生影响时的收益，与互联时彼此决策对其他微电网产生影响时的收益进行比较。当彼此之间不存在电能联通关系时，互联互通的运营就不复存在，缺电或富余状态下仅与配电网有电能传输关系，其分析结果如表3、表4所示。

表3 博弈前后互联微电网收益-成本等年值分析结果

表4 互联微电网分布式发电单元纳什均衡配置数量

由表中等年值计算结果可知，微电网在通过博弈优化后收益增加明显。临近微电网通过投资建设软硬件设置，将新建或原有微电网改造构成互联互通供能体系，从而提高不同微电网投资主体的收益。

4.2 可再生能源消纳权重激励敏感性分析

现将可再生能源消纳责任权重激励额设为不同值，分析该比值对微电网优化配置方案的影响。计算结果如表5和表6所示。

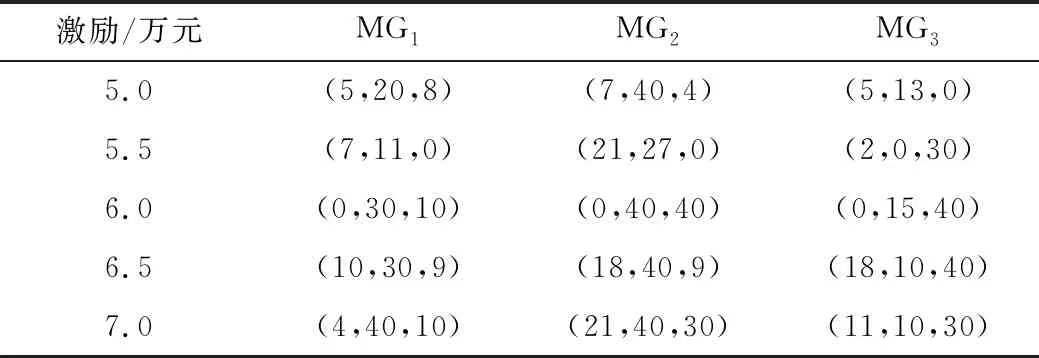
表5 可再生能源责任消纳权重激励额敏感性分析配置数量结果

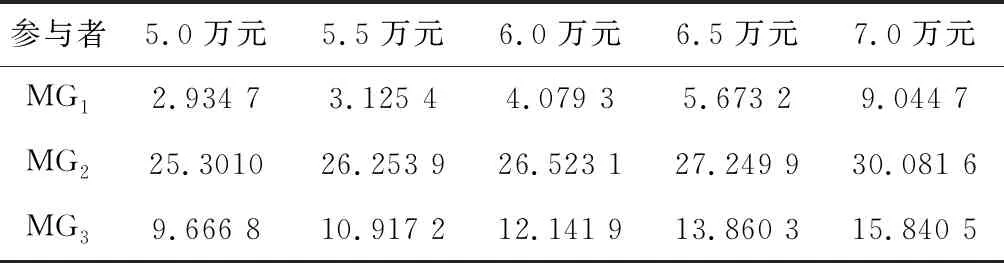
表6 可再生能源责任消纳权重激励敏感性分析

由表5与表6中的数据可以看出，典型风-光-储微电网本身作为清洁能源产销者，提高了可再生能源责任消纳权重的激励。对微电网而言，提升了其可再生能源装机的配置，增加了各个微电网主体的收益。所以，对于典型的风-光-储微电网而言，提高可再生能源消纳权重的比重，对其配置可再生能源发电单元与消费绿色电力具有可观的推动作用。

4.3 储能成本敏感性分析

现将储能电池成本设为不同值，分析储能价格对优化配置方案的影响，为不同微电网主体的储能电池装置优化配置提供参考。

由表7与表8可以看出，随着储能电池单位价格的降低，微电网投资开发者的收益增加，成本减少，储能安装数量整体呈上升趋势。当交易价格为定值时，储能电池成本下降，使其参与互联微电网的电能交易次数增加。当微电网在运营出现缺电情形时，通过其他微电网供电功率会随着储能电池参与供能而增加，进而降低互联微电网同配电网之间的交换电量。高价从配电网侧购买远距离传输的电能会大幅减少，这也是储能电池配置增多、成本增加，而各微电网收益也同时增加的原因之一。

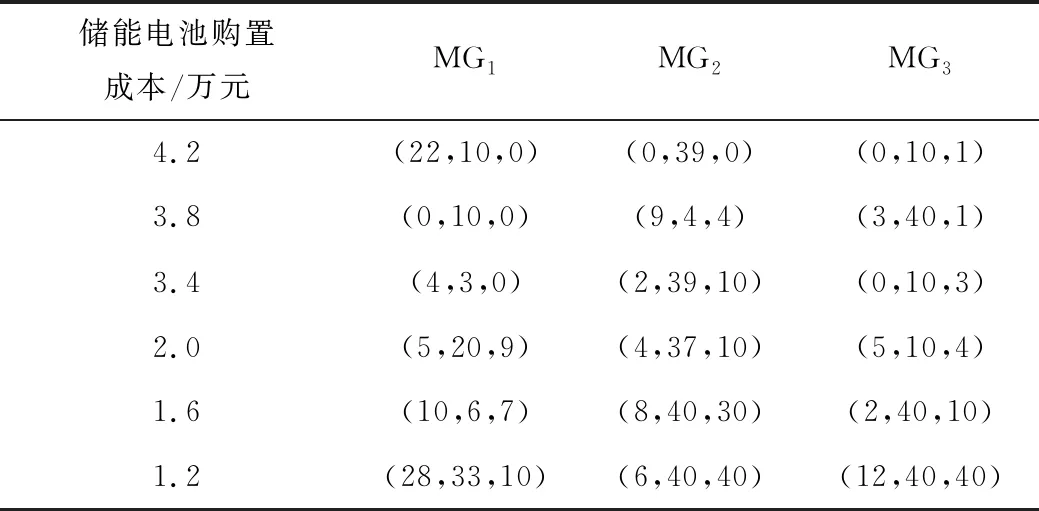
表7 储能电池成本敏感性分析的配置结果

表8 储能电池成本对各自微电网收益-成本影响分析

5 结束语

本文研究了区域配电网侧的典型风-光-储微电网特征，并在考虑了多个微电网分属不同投资运营主体的情况下，详细分析了互联微电网各主体收益的影响因素与关系，建立了基于不同利益主体的互联微电网收益-成本博弈经济模型。本文采用博弈分析的方法，分析了互联微电网中的分布式发电单元优化配置。通过算例分析，讨论了基于非合作竞争博弈模式下的互联微电网优化配置方案，并通过敏感性分析探讨了相关参数对优化配置方案的影响。算例结果表明，当微电网互联互通时，不同微电网的分布式发电单元决策投资建设量对其他微电网将产生影响。各个微电网通过配置合适的风力发电单元、光伏发电单元与储能电池单元容量使自身收益达到最优，辅助不同微电网投资运营主体做出投资建设决策。对可再生能源消纳权重激励以及储能电池成本的敏感性分析，可以为微电网设计者提供参考。