目标覆盖中基于权重的最大网络寿命算法

周 佳，王 然

(杭州电子科技大学 计算机学院,浙江 杭州 310018)

覆盖问题是无线传感网络中的常见问题。根据所监测实体的不同，覆盖问题被分为区域覆盖[1-3]、目标覆盖[4-6]和栅栏覆盖[7-8]等问题。传感器监测模型分为0-1圆盘模型和概率模型。传感器类型分为全向传感器和定向传感器。

与传统0-1监测模型不同，概率监测模型是一种更加接近实际的监测模型[9]。传感器对目标的监测结果并不是确定的0或者1，而是一个与传感器材质和距离相关的概率。文献[10]研究了在概率目标覆盖中的最少节点选择问题，通过每次选择增益最多使传感器形成覆盖集合。文献[11]提出了在栅栏覆盖中的一种概率模型，通过网络流的方法得到最小权重的栅栏。文献[12]研究了在可移动传感器网络中使用概率模型的方法，通过将传感器节点分类，每一轮重新规划传感器位置使各个目标周围传感器更加均衡，以此来延长网络寿命。

定向传感器已被应用到越来越多的领域中，例如摄像传感器、红外传感器[13]。文献[14]中使用了一种非重叠定向监测模型。该模型中，传感器的监测角固定，偏转角可以是预设的几个方向之一。该研究使用遗传算法来确定每一轮应该开启的方向，通过多轮迭代得到最大网络寿命。文献[15]提出了一种非重叠定向模型，给定传感器的监测角后，可以根据实际情况偏转任意角度。文献[16]提出了在栅栏覆盖中使用定向传感器，并以此构造强栅栏覆盖。该研究考虑了在一维直线和二维平面情况下使传感器的偏转角度总和最小。

上述文献在求解网络寿命时，都没有考虑到目标权重的影响。本文研究了概率感知模型下的定向目标覆盖的最大网络寿命问题，考虑了目标的权重对网络寿命的影响。每一轮得到新的定向覆盖集合，通过多轮睡眠唤醒调度使总的网络寿命最大。

1 问题定义

1.1 监测模型

非重叠的概率定向感知模型对应的数学表达式如式(1)所示。其中，α为与传感器材质和功率相关的强度系数；di,j表示传感器和目标的距离；φs和φa分别表示传感器和目标与水平方向的夹角；θ表示传感器监测的张角。

(1)

对于任意一个传感器，可以用对应的四元组表示，即γi=(Li,Rs,θ,k)，分别对应了位置、监测半径、监测角和选择的方向。一旦确定这几个元素就能够知道目标是否被监测，以及对应的监测概率。对于偏转角和方向选择的关系如式(2)所示，传感器的监测范围为φs～φs+θ。

φs=(k-1)·θ

(2)

如图1所示，此时传感器有3个可选择的方向，对应的监测张角为120°。此时传感器偏转到了方向2，可以监测到目标a1,对应的偏转角为120°。目标a2虽然在监测半径的范围内，但是不在对应的方向内，所以无法被监测到。a3在对应的方向，但是其与传感器的距离已经超出了监测半径，所以也无法被监测。

图1 概率定向模型

如果目标aj在距离Rs之内的所有传感器集合为Ω，要使a至少满足的监测概率为ε，那么必然会有式(3)对应的关系。

1-∏si∈Ω(1-pi,j)≥ε

(3)

对式(3)进行对数转换可以得到如式(4)所示的对应计算式。

1-ε≥∏si∈Ω(1-pi,j)⟹
ln(1-ε)≥∑si∈Ωln(1-pi,j)⟹
-ln(1-ε)≤∑si∈Ω-ln(1-pi,j)

(4)

通过数学变化可以将概率转化为对数形式的累加。-ln(1-ε)表示增益阈值，对应每个目标的最低概率要求，使用Ψ来表示。传感器si对目标aj的概率则可以用-ln(1-pi,j)形式的增益等价代替，被定义为传感器si对目标aj的监测增益，用gi,j来表示。

1.2 形式化定义

定义1阈值半径。传感器si对目标aj必然存在距离d使得pi,j=ε，那么只要传感器和目标的距离小于d，必然能够直接满足监测概率要求。这个距离被定义为阈值半径，用Rm表示。阈值半径的计算式为

(5)

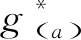
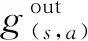
在图2中，s1和s2对目标的增益分别为3.4和2.4。如果先开启s1监测目标，目标a的积累增益为3.4。再开启s2，a的积累增益变成5.8，超出了给定的阈值5.0。因此，s2对目标的有效增益为1.6，溢出增益为0.8。

图2 各种类型增益

定义5ε-定向覆盖。给定长为L、宽为H的区域，在这片区域里有给定的待监测目标集合A={a1,…,aN}和随机抛洒的传感器集合S={s1,…，sM}。S中的传感器都是定向传感器，需要从S中选择部分传感器开启某个方向，使所有目标达到最低的概率要求ε；

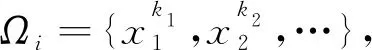
1.3 NP-hard证明

定理1ε-定向覆盖最大网络寿命问题是NP-hard问题。

文献[17]已经证明了在0-1模型下定向传感器大网络寿命问题是一个NP-hard问题，接下来通过概率模型到0-1模型的转化来说明ε-定向覆盖最大网络寿命问题也是NP-hard。如图3所示，假设s1、s2和s3是半径为Rs的定向传感器，采用的是概率感知模型。此时传感器对应的阈值半径为Rm，那么显然无论开启s1、s2和s3中的任意一个都能够使目标a直接满足概率要求。如果将s1、s2和s3替换成监测半径为Rm的定向0-1模型传感器，也是只需要开启任何一个都能够达到监测目标的效果，由此可见这两种形式是等价的。即任意半径为Rm的定向0-1覆盖问题都会有对应半径为Rs的定向ε-定向覆盖问题。

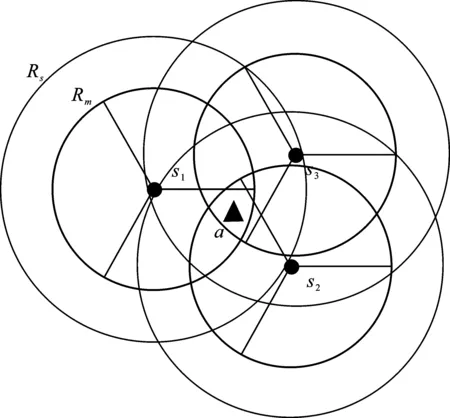
图3 NP-hard证明

综上，以感知半径为Rm的确定0-1定向传感器只是半径为Rs的概率定向传感器的一种特殊情况。所以本文提出的最小ε-定向覆盖最大网络寿命问题也是一个NP-hard问题。

1.4 目标和约束条件

式(6)～式(8)通过精确的数学表达式来描述ε-定向覆盖最大网络寿命问题，包括了最终的优化目标和所需满足的约束条件。

(6)

(7)

(8)

(9)

xi,w,k∈{0,1},τk>0

(10)

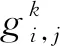
2 算法设计

本文已经证明了ε-定向覆盖最大网络寿命问题是一个NP-hard问题，无法在多项式的时间内找出最优解，因此需要提出与之对应的启发式算法。这个问题的关键就在于ε-定向覆盖集合的选择。如果每次迭代都能够选择出优秀的传感器集合，必定能够提高能效，延长整体的网络寿命。因此，本文提出了基于目标权重的优先选择算法(Target Weight Preference Algorithm，TWP)。

2.1 基于目标权重的优先选择算法

图4 潜在积累增益的差距

通过潜在可行增益来确定权重，权重越大说明应该优先考虑。权重的计算如式(11)所示，其中v表示所有节点的平均增益。首先按照目标为基准，逐个计算出权重，将目标按照权重进行排序。按照排序的顺序得出目标周围距离小于Rs的传感器集合，从集合中选择一个传感器开启对应的方向。节点的选择需要综合考虑剩余能量和有效增益，因此使用式(12)来计算优先系数。对于传感器si，其优先系数会综合考虑到剩余能量和总增益大小，使用hi来表示。

(11)

(12)

图5给出了为选择传感器的实例。目标a能够被两个传感器监测，假设a对应的集合就是{s1,s2}，g(s1,a)=2，g(s2,a)=3.2，总能量为10且s1和s2剩余能量分别为8和2，那么相应的ρ1=1.6，ρ2=0.64，最终所选择的传感器应该是s1。由此可见单纯的增益和能量都无法代表传感器的优先级，只有综合两类因素最优的才会被选择。

图5 传感器选择的举例

TWP算法首先需要得到每个目标周围的传感器集合，然后计算出目标的潜在积累增益，并使用潜在积累增益计算权重，按照权重为目标排序。对于某个目标周围的传感器集合，要优先开启优先级最高的传感器。而优先级的计算方式已经在式(12)中定义，开启一个传感器对应方向后就可以更新一个或多个目标的积累增益。为了使当前目标达到增益阈值，要按照优先级选择多个传感器。当完成一个目标后，就可以按照顺序为下一个目标寻找传感器集合，并通过同样的方式得到开启的传感器。当所有目标都迭代完成以后，就会得到每个目标的监测集合，合并之后即为完整的覆盖集合。当一轮完成后，需要更新传感器剩余能量，如果有传感器能量耗尽，就需要重新更新权重。

假设给定给的时间片为t，如果传感器剩余能量充足，那么当前这一轮就可以直接运行时间t。对于第i轮调度运行的时间τi如式(13)所示，其中min (RE(si))表示当前这轮选择的传感器集合中剩余能量最小的，es表示单位运行时间t需要的能量。

(13)

TWP算法的具体步骤如下：

输入传感器集合S；目标集合A；时间片t；最低监测ε；增益阈值Ψ；单位时间能耗es；监测半径Rs；初始能量Es。

输出运行的总时间T。

初始化变量：T←0

1.while each target can be covered do

3.Ω←Ø

4.计算每个目标的潜在积累增益

5.通过公式11得到目标权重

6.将A中目标按照权重排序

7.fora∈Ado

8.计算a周围距离小于Rs的集合φa

9.计算a对应于传感器的方向

10.从φa中重复选择hi最大的传感器s

11.开启s对应的方向

12.更新s能监测的所有目标增益

13.Ω←Ω∪s

14.end for

15. end while

16.计算Ω中剩余能量能否满足t

17.if satisfyτi=t

19.更新Ω中传感器运行τi后的能量

20.T←T+τi

21.end while

2.2 算法分析

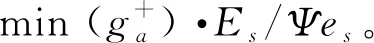
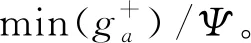
定理3TWP算法的时间复杂度为O(M×N+MlogM)。

在为目标计算潜在积累增益时，需要为M个目标计算周围的传感器集合。由于无法确定目标周围传感器数量，那么最多可能会有N个传感器，需要计算的次数为M×N。在根据潜在积累增益进行排序，时间复杂度为MlogM。最后按照顺序为每个目标先择传感器，需要计算优先系数。每个目标最多需要计算N次，那么M个最多目标需要计算M×N次。而调度的轮次假设为K，综合总的需要时间为K(M×N+MlogM+M×N)。由于K必定是一个常数，所以时间复杂度为M×N+MlogM。

3 模拟实验

实验中所有传感器都是随机抛洒到100 m×100 m的区域中，监测半径为15 m，默认设置的监测角为2π/3。与传感器物理特性相关的系数α为0.05，默认最低监测概率为ε=0.85。默认放置的传感器数量为200，目标数量为50，传感器初始能量为15 kJ，在时间片t全向开启(这里的单位时间指的是比较长的一段时间)时监测能耗为6 kJ。能耗与监测角度相关，例如监测角为π时的能耗是监测角为2π时的一半。为了保证准确性，所有实验都是在50次随机结果下的平均值。

图6表示在不同监测角下网络寿命随着传感器数量的变化，设置的监测角分别为2π、π、2π/3、和π/2。可以看到随着节点数量增加，网络寿命都会延长。监测角越小，对应的网络寿命也更长。这是由于监测角越小对应的能耗越小，减少了能量的浪费。

图6 不同监测角的比较

图7为不同目标数量下，网络寿命随着传感器数量的变化。监测角设定为2π/3，最小监测概率为ε=0.85。可以看出需要监测的目标数量越多，对应的网络寿命就越小。这是由于目标增多后，每一轮选择的覆盖集合对应的传感器数量会增加，对应的总能耗会增大。

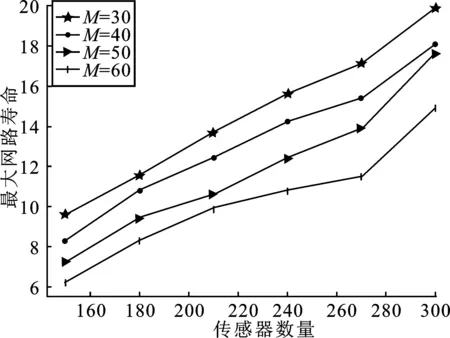
图7 不同目标数量的比较

图8中将TWP算法与文献[15]中的HMCS算法和文献[10]中的PSCM算法进行了比较。监测角为2π/3时，在不同的最小监测概率下最大的网络寿命如图8所示。随着目标监测概率的提高，网络寿命会逐渐变小，这是因为随着增益阈值变大单个目标周围需要开启的传感器数量增加了。从结果可以看出，TWP算法比另外两种算法表现更加优异。

图8 不同算法网络寿命的比较

图9显示出了3种算法在不同初始传感器数量下调度结束之后剩余能量的方差。可以看出，TWP算法由于考虑到权重更小的瓶颈节点，所以能量使用更加均衡，这也是其能够延长网络寿命的重要原因之一。

图9 不同算法剩余能量方差

4 结束语

本文研究了概率定向传感器的目标覆盖问题，并提出了最大网络寿命的优化目标。为了解决这个问题，本文将概率转化为增益，提出了积累增益、有效增益等概念，并证明了这是一个NP-hard问题。本文提出了基于权重的优先选择算法，将潜在积累增益转化为权重，并将权重应用到目标排序和节点选择的过程中。最后，通过对比实验证明了本文所提出算法的有效性。