间隙原子在核石墨中迁移与结合规律的模拟计算

2021-06-16徐海婷吴喜军张铭军彭志华

核技术 2021年6期

徐海婷吴喜军刘卫谭捷杨果邓柯张铭军钱楠彭志华

1（南华大学数理学院衡阳421001）

2（中国科学院上海应用物理研究所上海201800）

核石墨作为中子慢化剂、反射层、燃料球包覆材料以及堆内结构材料被广泛应用于各型反应堆中［1］。反应堆中的核石墨除承受常规工程结构材料的负荷外，还需承受大剂量中子辐照，从而产生大量间隙原子并稳定存在于表面（称为吸附碳原子）或石墨片层之间［2］。间隙原子是从规则碳晶格点中被溅射出来沉淀在石墨层间或表面的点缺陷，因其存在未饱和的碳键，导致核石墨的性质活泼、结构多变［3-5］。近年来，研究人员利用第一性原理［6-7］或分子动力学方法［8-9］探索石墨中间隙原子的稳定结构，计算不同亚稳结构之间的能垒，如Zhou等［10］利用高温分子动力学（Molecular Dynamics，MD）和自适应动态蒙特卡罗（a Kinetic Monte Carlo，a-KMC）方法研究螺旋间隙原子在石墨片层内和层间的迁移与结合行为。有研究表明，间隙原子之间以及与石墨片层间的相互作用不可避免地会影响间隙原子的结构［11］，但其发生的内在机制尚不明确，深入研究间隙原子结构变化的内在机制，对确定核石墨寿命具有重要的参考意义。

综上所述，目前对核石墨层间间隙原子等点缺陷的迁移与结合行为的研究还很少，对核石墨间隙原子的构型与演化尚不十分明确。第一性原理计算方法仅需要微观体系中各元素的原子种类和排列，就能得出微观体系的一些性质，可计算材料结构参数和构型、状态方程和力学性质、电子结构、光学与磁学性质等［12］。因此，本研究将基于第一性原理研究间隙原子间的相互作用，以及间隙原子迁移、结合行为，为理解石墨片层的生长机制、调整其物理性质提供重要信息。

1 计算方法

基于密度泛函理论（Density Functional Theory，DFT）［13］的维也纳从头计算模拟软件包-VASP［14-16］用来对体系的性质进行计算。前人在研究H［17］、等原子（或分子）在石墨表面的吸附行为时发现，相邻两层石墨层间的范德瓦尔斯作用力相对于石墨表面的吸附行为的影响可以忽略，为避免周期性边界条件导致的镜像作用，构建了一个包含72个碳原子的6×6石墨烯超胞模拟石墨表面，并在考虑范德瓦尔斯作用力的基础上构建了一个包含144个碳原子的6×6双层石墨片层超胞模拟石墨层间。模型的三个方向都采用周期性边界条件，超胞Z方向大小为1.50 nm，采用投影缀加波赝势（Projector Augmented Wave，PAW），交换关联作用使用的是广义梯度近似（Generalized Gradient Approximation，GGA）PW91［19］，平面波的截断能为450 eV，布里渊区积分的K点取样采用Gamma点居中的网格，网格大小为4×4×1。采用能量收敛标准为10-6eV、力收敛标准为0.1 eV·nm-1的共轭梯度方案进行结构优化。扩散能垒通过爬坡弹性带方法（Climbing Image Nudge Elastic Band，CI-NEB）估算的［20-22］，结构优化后的石墨晶格常数为0.246 6 nm，和实验值（a=b=0.246 4±0.000 2 nm）相吻合［23-24］。

同一石墨片层上间隙原子间的相互作用能定义为［25］：

式中：Ef2C和EfC分别为两个间隙原子和单个间隙原子吸附在同一石墨片层上的形成能，它们分别定义为：

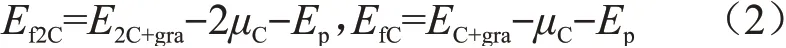
式中：E2C+gra、EC+gra、Ep和μC依次为同一石墨片层上有两间隙原子的石墨结构总能量、只有一个间隙原子的石墨结构总能量、完美石墨结构总能量和一个碳原子的化学势。

2 结果与讨论

2.1 石墨中的间隙原子

基于石墨烯超胞构建了吸附在石墨表面的间隙原子（也称为吸附碳原子）结构模型，分析对比了碳原子上方的顶位、碳碳键上方的桥位以及六元碳环上方的穴位三种可能位点的结构稳定性，结果表明：碳原子在石墨表面的稳定结构是与片层上两相邻的碳原子成键，即桥位的吸附形态（图1（a）），这与文献［26］报道的实验现象一致。计算表面吸附碳原子形成能与迁移能的结果表明，石墨表面吸附一个碳原子的形成能为6.550 eV与文献［27］的理论计算值6.640 eV相吻合，迁移能为0.390 eV与文献［28］的理论计算值0.470 eV相吻合。

此外，基于双层石墨片层超胞构建了层间间隙原子的结构模型，计算表明：间隙原子在石墨层间存在两种稳定形态。一种是只和一片层上两相邻的碳原子成键即桥位间隙原子（图1（b）），该结构中的两片层膨胀，在Z轴方向产生高达0.064 1 nm的形变量。另一种是与两相邻片层的4个碳原子成键，即螺旋间隙原子（图1（c）），两片层同时收缩，在Z轴方向产生0.056 1 nm的形变量。桥位间隙原子与螺旋间隙原子形成能的计算结果分别为7.290 eV和5.693 eV，与文献［27］给出的数据7.680 eV和6.200 eV符合较好。螺旋间隙原子的形成能比桥位间隙原子的形成能低1.597 eV，这意味着螺旋间隙原子结构比桥位间隙原子更稳定。

图1 核石墨中常见的间隙原子结构 (a)表面吸附碳原子，(b)桥位间隙原子，(c)螺旋间隙原子Fig.1 Typical structures of interstitial atom in nuclear graphite(a)Surface adsorption of carbon atoms,(b)Bridge interstitial atoms,(c)Spiro interstitial atoms

2.2 间隙原子相互作用

因间隙原子在石墨中存在较显著的聚集和结合现象，有必要弄清间隙原子在同一片层上迁移的动力和趋势。计算表明，间隙原子在相邻两个石墨片层内的迁移能垒为1.530 eV（文献［10］报道的为1.740 eV，图2），比其在同一石墨片层的迁移能垒0.390 eV要高得多（图3）。一个间隙原子从两个相邻石墨片层中间沿Z轴方向迁移到其中一个石墨片层表面的过程，反应能为-1.338 eV（图2），而间隙原子在同一石墨片层中迁移的反应能不变（图3）。可见间隙原子更倾向于在同一石墨片层上迁移，且石墨内部的间隙原子迁移到石墨表面后其结构能量会降低。因此，本文主要研究同一石墨片层上间隙原子的相互作用。

采用吸附于表面的间隙原子（即吸附碳原子）来研究间隙原子的相互作用。使用的计算模型由两个沿锯齿形（或扶手椅形）方向吸附于不同位点的间隙原子和6×6石墨烯超胞构成。按式（1）计算了两间隙原子沿锯齿形（或扶手椅形）方向上不同距离的相互作用能（表1）。

表1 只给出了距离大于0.3 nm的间隙原子间相互作用能，因为小于此值时两间隙原子会直接成键，结果表明：无论是沿锯齿形方向还是沿扶手椅形方向上的相互作用力均为引力，且沿锯齿形方向上的引力略小于沿扶手椅形方向上的引力，距离越大相互作用能越小，且当两个间隙原子距离大于0.5 nm时，相互作用能可以忽略。

表1 同一石墨片层上两个间隙原子相互作用能Table 1 Interaction energy of two interstitial atoms on the same graphite sheet

图2 单个间隙原子在相邻石墨片层间的迁移能垒Fig.2 The energy barrier for the migration of a single interstitial atom between adjacent graphite sheets

图3 单个间隙原子在同一石墨片层中的迁移能垒Fig.3 The energy barrier for the migration of a single interstitial atom in the same graphite sheet

2.3 间隙原子的迁移与结合

鉴于间隙原子在一定的距离内存在引力作用，为探索石墨片层中间隙原子的聚集、结合直至形成新的片层的内在机制与规律，模拟了间隙原子在石墨中的迁移与结合行为。首先模拟计算了石墨表面上的间隙原子沿锯齿形（或扶手椅形）方向迁移直至与另一间隙原子结合的过程（图4或图5），图中B0位点放置一个间隙原子，鉴于两个间隙原子距离大于0.5 nm时，相互作用能可以忽略，所以另一间隙原子选在位于沿锯齿形（或扶手椅形）方向路径上的第5近邻的B5位点，然后计算处在该位点上的间隙原子沿B5→B4→B3→B2→B1的迁移、结合等反应过程，获得了各过程中反应能垒。因两迁移路径上的B2、B1两位点与B0位点相距太近属于不稳定位点，所以一个间隙原子从B5位点沿两条路径迁移止步于B3位点，而后就是结合的过程，结合反应后两碳原子键合成链状吸附于B1位点并垂直于表面。从图4可看出，沿锯齿形方向上迁移的最高反应能垒是0.428 eV，发生在第一个间隙原子从B5→B4的迁移过程中，而处于B3、B0位点的两间隙原子结合反应能垒为0.102 eV，结合反应后的结构能量比迁移之前降低多达6.035 eV。

图4 间隙原子沿锯齿形方向路径的迁移、结合反应过程Fig.4 The migration and combination reaction process of interstitial atoms along the zigzag direction

图5 间隙原子沿扶手椅形方向路径的迁移、结合反应过程Fig.5 The migration and combination reaction process of interstitial atoms along the armchair direction

从图5可知，沿扶手椅形方向上迁移的最高反应能垒为0.405 eV（比沿锯齿形方向低0.023 eV），发生在第一个间隙原子从B4→B3位点的迁移过程中，处于B3、B0位点的两间隙原子结合反应能垒为0.018 eV（比沿锯齿形方向低0.084 eV），结合反应后的结构能量比迁移之前降低5.984 eV（沿锯齿形方向为6.035 eV）。可见，相对于沿锯齿形方向路径来说，石墨表面的间隙原子更倾向于沿扶手椅形方向路径迁移、结合。两间隙原子键合后其结构能量会显著降低（6.0 eV左右）并成链状垂直于石墨表面。同时，还计算了两个间隙原子成链状整体迁移至相邻桥位的能垒，发现比单个间隙原子的迁移能高0.47 eV，说明单个间隙原子较易迁移。鉴于石墨片层间的作用力相对于碳原子的迁移、结合动力来说可以忽略，所以可推断上述结论同样适用于间隙原子在石墨片层间迁移与结合的行为特征。

图6 （a）是石墨表面两个间隙原子结合后的稳定结构的侧视图，当有第三个间隙原子按上述迁移路径迁移并与之结合后，会出现图6（b）和图6（c）的两种结构，分别是三个间隙原子成正三角形位于六元碳环的穴位以及成倒三角形位于一个碳原子顶位的结构。图6（c）结构的能量比图6（b）的低1.341 eV，比结合反应发生前的结构能量低4.581 eV，因此图6（c）结构是石墨表面由三个间隙原子组成的最稳定团簇结构。当结合的间隙原子继续增加直至第6个时，这些聚集的间隙原子都会以链状吸附于桥位，结合形成6个间隙原子的链状结构（图6（d））。作为对比，构建了正六边形的六元碳环和底面石墨片层分别以AA、AB堆垛形态的结构模型，结构优化后分别对应图6（e）、图6（f），其中图6（f）对应的结构能量比图6（d）的低3.077 eV，比图6（e）的低0.025 eV，且两种结构中的六元碳环都发生了较大的形变，六元碳环和底面石墨片层AB堆垛时相距0.335 3 nm比AA堆垛时近了0.006 5 nm。这意味着石墨表面的间隙原子结合聚集的数目超过6个时，会倾向于演化成包含六元碳环的团簇结构与底面石墨片层以AB堆垛的形态存在，如果团簇结合更多的碳原子最终会形成新的石墨片层。

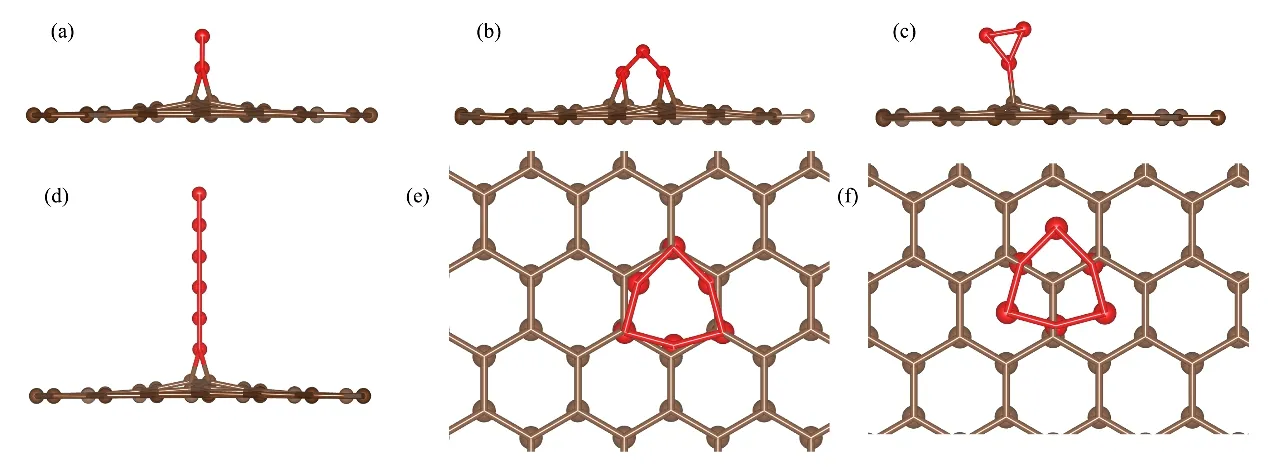
图6 优化后的石墨表面上间隙原子的结构 (a)链状的两个间隙原子，(b)亚稳的三个间隙原子团簇，(c)稳定的三个间隙原子团簇，(d)链状的六个间隙原子团簇，(e)六元碳环与底面成AA堆垛，(f)六元碳环与底面成AB堆垛Fig.6 The optimized structures of interstitial atoms on graphite surface (a)Two interstitial atoms chain,(b)Metastable three interstitial cluster,(c)Stable three interstitial cluster,(d)Cluster of six interstitial atoms chain,(e)Six-membered carbon ring and the bottom surface are stacked in AA,(f)Six-membered carbon ring and the bottom surface are stacked in AB

本次研究还模拟了石墨层间间隙原子的结合、演化规律。计算结果表明：石墨层间两个间隙原子结合后存在三种结构，分别是两紧邻的桥位间隙原子结构（图7（a））、两紧邻的螺旋间隙原子结构（图7（b））以及链状的两间隙原子结构（图7（c））。其中，图7（c）的结构能量比图7（b）的低0.379 eV，比图7（a）的低0.025 eV。说明石墨层间成链状的两间隙原子结构最稳定，这与文献［10］的结论一致。图7（d）是文献［10］中报道的亚稳结构，本次研究发现该图中的两间隙原子继续靠近后，C-C键会完成从sp3杂化向sp2杂化的转变，同时两个碳原子与石墨片层成键（如图7（b）所示），能量降低1.282 eV。另外，亚稳结构除了紧邻的螺旋间隙原子结构外（图7（b）），还包括两紧邻的桥位间隙原子结构（图7（a））。

图7 优化后的石墨层间间隙原子结构 (a)两紧邻的桥位间隙原子，(b)两紧邻的螺旋间隙原子，(c)链状的两间隙原子，(d)文献[10]报道的两紧邻螺旋间隙原子Fig.7 The optimized structures of interstitial atoms in graphite interlayers (a)Two closely adjacent bridging interstitial atoms,(b)Two closely adjacent spiro interstitial atoms,(c)Two interstitial atoms chain,(d)Two adjacent spiro interstitial atoms reported in Ref.[10]

当有第三个间隙原子与上述稳定结构结合时，会生成包含三个间隙原子的团簇结构（图8）。它们分别是在链状的两间隙原子结构（图7（c））基础上生成的图8（a）和（c）所示结构，以及在两紧邻的螺旋间隙原子结构（图7（b））基础上生成图8（b）所示结构。其中图8（c）对应结构能量比8（b）的低2.113 eV，比图8（a）的低0.185 eV，说明石墨层间三个间隙原子形成的团簇中以链状结构最稳定，这也与文献［10］的结论一致。图8（a）可视为由链状的两间隙原子+螺旋状间隙原子构成的亚稳结构。此外，与图7（b）类似，文献［10］中报道的亚稳结构（图8（d））也可以变形成更稳定结构（图8（b）），其结构能量降低3.714 eV。可见，无论是在石墨表面还是石墨层间，间隙原子会发生迁移、结合形成包含六元碳环的团簇，最终会形成新的石墨片层，且这一过程将明显降低系统的结构能量。

图8 优化后的双层石墨间隙原子的结构 (a)链状的两间隙原子+螺旋状间隙原子，(b)三个紧邻螺旋间隙原子，(c)成链状的三个间隙原子，(d)文献[10]报道的三个紧邻的螺旋间隙原子Fig.8 The optimized structures of interstitial atoms in doublelayer graphite (a)Two interstitial atoms in a chain and spiro interstitial atoms,(b)Three closely adjacent spiro interstitial atoms,(c)Three interstitial atoms in a chain,(d)Three adjacent spiro interstitial atoms reported in Ref.[10]