基于神经网络的CFD粗网格模拟优化方法研究
2021-06-16刘晓晶
靳 爽 刘晓晶 程 旭
(上海交通大学 核科学与工程学院 上海200240)
在反应堆计算流体力学(Computational Fluid Dynamics,CFD)数值模拟中,计算精度和计算时间是一对突出的矛盾。为了能够较好地兼顾计算效率和计算精度,实现在较高计算效率下取得满意的计算结果,研究人员尝试了多种新技术方法,比如并行计算、对网格划分方式进行优化[1-2]等。随着大数据和人工智能等领域的发展,机器学习也成为解决上述问题的一种可行路径。一方面,大量先前已有的数值模拟结果、理论研究成果和实验结果积累为数据训练提供了广泛的训练资源;另一方面,随着反应堆热工水力研究和应用的不断发展,对“物理过程相似、工况参数不同的大批量多组工况”的CFD数值模拟需求日益凸显,例如研究多种不同入口速度下的棒束流动传热CFD结果、多种摇摆条件(摇摆俯角、摇摆周期的各类组合)下的反应堆CFD计算结果等,在该类问题中,基于神经网络的CFD粗网格模拟优化方法对于“实现在较高计算效率下实现较高精度的数值模拟”具有显著效果。
根据美国爱达荷国家实验室于2018年发布的报告[3],在数据驱动的机器学习架构中可以使低分辨率的模型计算出高分辨率模型下的模拟结果,并对绝热腔室中射入空气湍流模拟结果进行了优化。目前,通过机器学习针对反应堆热工水力数值模拟进行优化的案例研究还较少,本文拟应用机器学习方法,针对粗网格下5×5棒束出口截面冷却剂子通道温度的CFD结果进行优化,以期为机器学习方法在反应堆热工领域实现较高计算效率和较高计算精度的数值模拟应用提供参考。
1 数值模拟优化方法
1.1 棒束模型
本文计算的棒束模型是截短型组件的5×5棒束栅元,其主要参数参考一体化模块小型反应堆常用的截短型组件参数而设定[4-7],如表1所示。
针对本文计算的棒束模型,可以划分为36个子通道,从左上到右下依次编号为子通道1(sub 1)、子通道2(sub 2)、……、子通道36(sub 36),如图1所示。

表1 5×5棒束栅元主要参数Table 1 Main parameters of 5×5 rod bundle

图1 5×5棒束栅元子通道划分方式Fig.1 Subchannel division method of 5×5 rod bundle
1.2 问题描述
本文旨在对不同入口速度工况中出口截面上36个子通道各自的平均温度值进行修正,粗网格和细网格均采用STAR-CCM中的结构化定向网格[8],基础网格为多边形网格,对于边界层处的网格,均使用棱柱层网格生成,粗网格和细网格下均设置棱柱层层数为三层,棱柱层增长率取默认值1.5,棱柱层总厚度取默认值即网格尺寸基数的33.3%。其网格参数的具体设置如表2所示。
细网格参数的选取达到网格无关性的要求,基础尺寸为0.5 mm、0.6 mm、0.7 mm网格下的子通道1、子通道2、子通道16(分别为角通道、边通道、中心通道)的温度计算结果如表3所示。
本文根据入口速度的不同,将20组工况作为训练组用于机器学习,另外5组工况作为验证组以检验修正的效果。其中,5组验证组工况中既包括相对于训练组的内含参数工况,也包括外延参数工况。训练组工况及验证组工况的入口速度设定情况如表4所示。鉴于本文计算的物理过程并不复杂,在本文涉及的计算工况中,所选用的湍流模型均为可实现的k-ε(Realizablek-ε)模型。

表2 粗网格参数和细网格参数Table 2 Parameters of coarse grid and fine grid

表3 网格无关性验证结果Table 3 Results of grid independence verification

表4 训练组和验证组工况入口速度设定情况Table 4 Inlet speed of training group and verification group working conditions
1.3 基于机器学习的优化方法
数值模拟的误差来源主要包括以下三类:第一类是由于物理简化和(或)数学近似导致的模型误差;第二类是由于网格的存在,导致守恒方程或源项在时空平均方法下产生信息丢失所引起的网格误差;第三类是由于迭代收敛、算法选择等原因引起的其他误差。
对于第一类误差,针对流体和壁面间传热、质量交换、动量交换等现象存在多种关系模型进行模拟,与网格尺寸相关的特征长度是这些模型中的一个重要参数。对于第二类误差,同样由网格尺寸决定。而第三类误差相较前两类误差对计算结果的影响要小得多。因此,数值模拟的误差与网格尺寸密切相关,且实际分析时往往无法区分模型误差和网格误差,应将其作为一个整体来考虑。
我们可以运用模式识别和统计分析等机器学习方法,从数据中直接获得容易被人忽视的信息,试图寻找到包括网格信息、模型信息、物理信息在内的参数与误差之间的定量关系。在此基础上,运用该定量关系对粗网格模拟结果进行修正,实现满足计算要求的快速数值模拟。
根据问题的需要,我们可以将模拟对象的几何参数、模拟工况的物理参数及数值计算的网格参数纳入机器学习的输入变量中。针对本文研究的工况,每组工况均采用同一套粗网格和同一套细网格,各组工况在进行CFD计算时选用的湍流模型、传热模型一致,仅有冷却剂入口速度设定不同。因此,本文通过机器学习需要得出的是入口速度、粗网格下出口截面各个子通道温度、细网格下出口截面各个子通道温度之间的隐含关系。
根据Chang等[9]的文章,目前数据驱动的热工水力模拟机器学习架构可以依据数值模拟是否包含偏微分方程、偏微分方程的形式是否已知、偏微分方程本身是否作为机器学习对象、模型的建立是否需要在不同尺度上分别进行等四项标准分成5种类型,本文的研究属于上述五种架构类型中的第二类,其主要步骤如图2所示。

图2 基于机器学习的数值模拟优化框架[9]Fig.2 Optimization framework for numerical simulation based on machine learning[9]
本文中,定义粗网格下子通道i(subi)的平均温度为TLi,作为待修正值;细网格下子通道i的温度记为THi,作为精确值(修正目标值)。定义误差函数如下:

根据前述的优化原理,将误差函数E i设置为如下的形式:

式中:V为冷却剂入口速度,子通道编号i=1,2,3,...,36,误差函数中的具体函数形式由机器学习方法得到。将粗网格计算结果按照误差函数修正后的子通道i的温度记为TMi,即有:

在机器学习方法的选择上,目前主要使用深度学习的方法。原则上,任何两层以上的神经网络都可以被认为是深度学习。Hornik等[10]在文章中论证了多层神经网络是一种通用方法,可以捕捉任何可度量信息的特性。神经网络包括卷积神经网络和前馈神经网络两种方式。其中,卷积神经网络通常具有更好的预测能力,但所需的数据训练量也更多。鉴于本文研究的工况相对简单,本文选用所需数据量较少的前馈神经网络。对于神经网络层数和神经元数量的选取,海军工程大学曹植珺等[11]的综述文章中指出目前缺少很好的参数调节的手段,包括训练神经网络时隐含层数、隐含节点数、输入节点数等基本依靠经验。对于不复杂的关系结构,神经网络的层数通常为2~3层,神经元数量不超过10个,本文选择的神经网络层数为两层,神经元数量为4个,其结构如图3所示。
第一层为输入变量层,包括工况冷却剂入口速度V以及粗网格下出口截面子通道温度TLi(i=1,2,3,...,36)共计37个输入变量;第二层为神经元层,共包括4个神经元N1,…,N4;第三层为输出变量层,包括粗网格与细网格下出口截面各个子通道温度的误差预估值E1,E2,…,E36,共计36个输出变量。根据神经网络的基本原理,各层元素之间的关系如下:

图3 前馈神经网络学习架构Fig.3 Framework of feedforward neural network(FNN)

式中:f为神经网络学习的函数形式,为表达方便,记:

本文采用均方根误差来评估优化效果,分别定义未经优化的粗网格下出口截面36个子通道温度与精确值(细网格下相应计算结果)之间的均方根误差为RMSEL,经过优化的粗网格下出口截面36个子通道温度与精确值(细网格计算结果)之间的均方根误差为RMSEM,其形式如下:

通过比较RMSEM与RMSEL的大小差异来评估优化效果,如果0~RMSEM≪RMSEL,则可认为达到预期优化效果。
2 优化结果
2.1 计算精度
使用机器学习得到的误差函数对训练组和验证组的粗网格结果进行优化前后,出口截面36个子通道温度与细网格下模拟结果的均方根误差如图4所示。
其中,5组验证组工况的粗网格结果优化前后的均方根误差如表5所示。

图4 粗网格结果优化前后的均方根误差Fig.4 Root mean square error(RMSE)before and after optimization
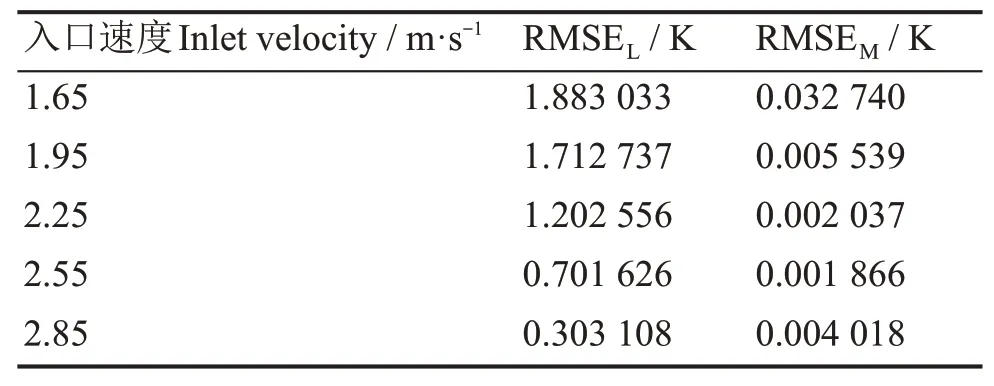
表5 验证组工况粗网格结果优化前后的均方根误差Table 5 Root mean square error before and after optimization of the verification group results
通过图4和表5可以看出,训练组和验证组粗网格下修正优化后的结果相比于优化前,与细网格下结果的均方根误差大大降低,5组检验组工况出口截面36个子通道温度均方根误差平均值从1.16 K降低为9.24×10-3K,满足0~RMSEM≪RMSEL,达到预期的优化效果。
以入口速度为2.25 m٠s-1的工况为例,其细网格下、粗网格下结果修正前后36个子通道的温度如图5所示。通过图5可以看出,修正优化后的各个子通道温度值相比于优化前,明显更加接近细网格下的结果;且对于边通道和角通道,优化提升的效果更加明显。
2.2 计算效率
使用本文的方法可以对粗网格下的计算结果进行修正,取得了良好的优化效果,这也使得CFD计算效率大幅提升。
对于粗网格、细网格工况,在运算时均以连续20个迭代步内出口平均温度变化不超过0.01℃为判断计算达到收敛的条件。本文涉及的表4中共计25个工况在粗网格、细网格下进行CFD运算所需要的总CPU系统时间如表6所示。
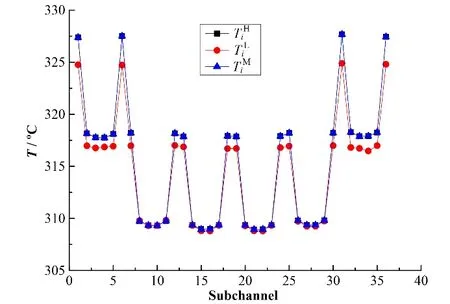
图5 V=2.25 m٠s-1工况下粗网格结果优化前后子通道温度值与细网格下结果的对比Fig.5 Comparison of subchannel temperature before and after optimization under the condition of V=2.25 m٠s-1
从表6可以看出,不同工况下粗网格计算所需的总CPU系统时间远远小于细网格下所需时间,上述25个工况粗网格下总CPU系统时间的平均值约为细网格下平均值的2.54%。就本文研究的问题而言,若需要得到入口速度从1.65~2.85 m·s-1间等距100个工况的计算结果,传统方法需运行100个细网格工况,而基于神经网络的粗网格优化方法下,仅需计算25个细网格工况和100个粗网格工况(以表6的CPU系统时间平均值计算,约相当于三个细网格工况的计算量),总体的计算效率得到大幅提高。
3 结语
本研究利用前馈神经网络的机器学习方法,对不同入口速度工况下出口截面子通道冷却剂温度粗网格下的CFD数值模拟结果进行了优化,得到如下结论:
1)采用神经网络方法对本文工况粗网格下的结果进行修正后,5组检验组工况出口截面36个子通道温度的均方根误差平均值从1.16 K降低为9.24×10-3K,误差大大减小,优化效果显著。
2)在本文研究的问题中,粗网格下总CPU系统时间的平均值约为细网格下平均值的2.54%。通过神经网络对粗网格结果优化的方式,对于批量化的CFD计算或者已有较为充分的训练数据的CFD计算,其计算效率将大幅提高。
3)就本文算例来看,基于前馈神经网络的机器学习框架对于内部预测(即验证工况的速度值在训练集速度值范围内)的优化效果好于外部预测。但由于本文算例较为局限,这一结论还需要更多算例结果的支持验证。
本文的研究为利用机器学习框架对粗网格数值模拟进行优化,从而兼顾计算效率与计算精度提供了可行参照。未来,可以在反应堆热工水力领域的更多问题特别是多耦合或非稳态问题上进行更广泛的验证。
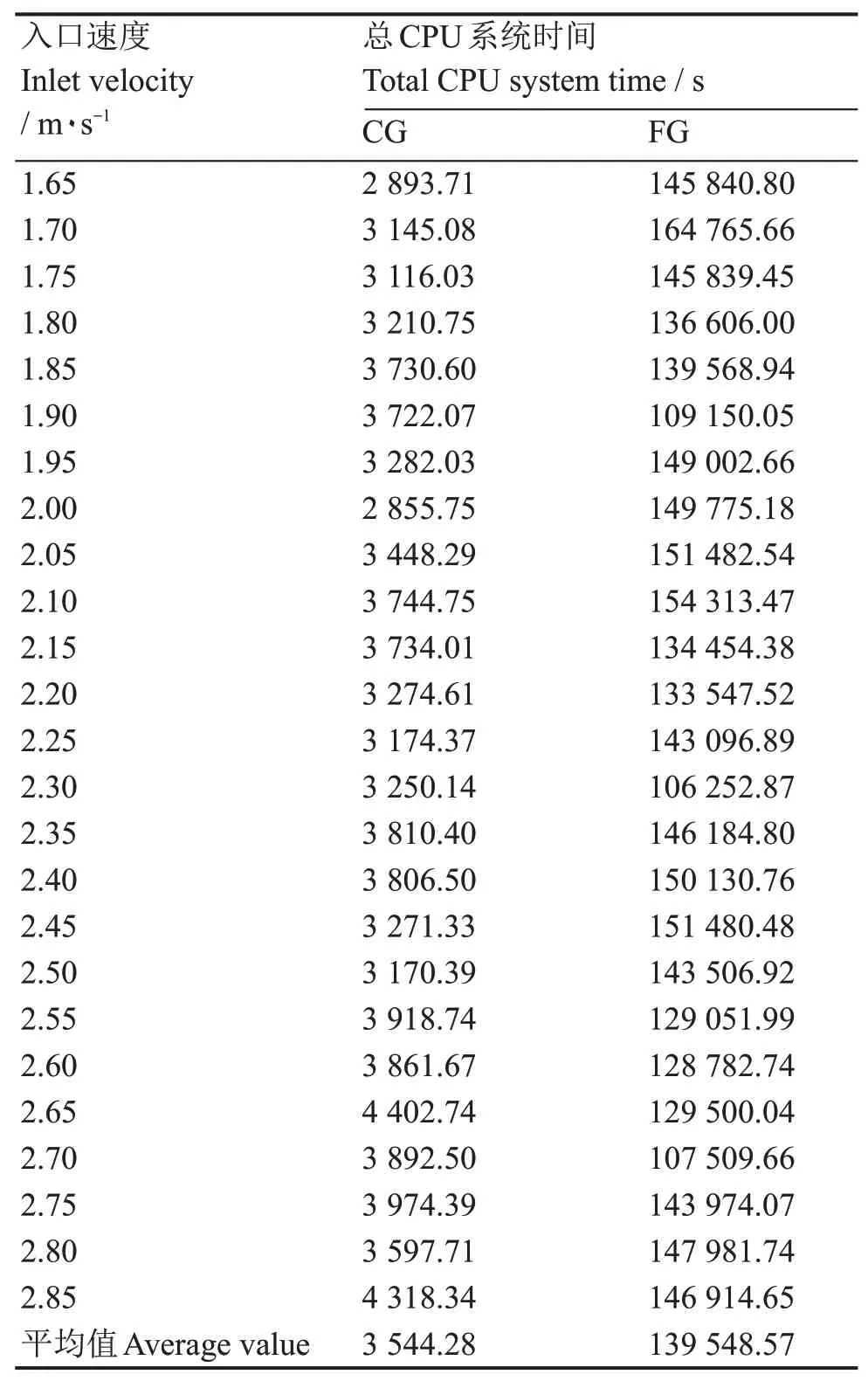
表6 25个工况在粗网格、细网格下运行所需的总CPU系统时间Table 6 The total CPU system time required for 25 operating conditions to run under coarse and fine grids
