基于VMD多尺度模糊熵的HVDC输电线路故障识别方法

王桥梅 ，吴 浩 ，2，3，胡潇涛 ，顾小平 ，陈佳豪

（1.四川轻化工大学自动化与信息工程学院，自贡 643000；2.人工智能四川省重点实验室，自贡 643000；3.企业信息化与物联网测控技术四川省高校重点实验室，自贡 643000）

高压直流输电技术在远距离、高电压输电方面具有的独特经济和技术优势，近几年在实际中得到了广泛的应用[1-2]。目前我国昌吉—古泉特高压直流输电线路电压等级已高达1 100 kV，输电线路全长达3 000多km。由于输电线路环境复杂，输送距离长，发生故障的几率高，因此有必要进一步研究稳定可靠、响应速度快的高压直流线路保护，以使电力系统稳定可靠运行[3-5]。

利用边界元件的阻抗幅频特性，文献[6-7]分析了滤波器单元对高信号的阻滞作用，提出利用单端特定频率信号构建区内外故障识别判据，该方法受控制系统触发角和换相叠弧角的影响较大；文献[8]利用直流输电系统固有的结构和参数，在理论上分析了直流线路的暂态测量阻抗特征，在特定频带内，区内或区外故障时整流侧和逆变侧的测量阻抗值差异明显；文献[9-10]则分别利用S变换提取测量波阻抗和波阻抗相位实现区内外故障识别，但该算法对采样频率和硬件设备要求较高；文献[11]利用线模电压反行波突变量构建区内外故障识别判据，利用线模和地模电压行波的比值实现故障选极，由于地模波易受噪声等因素干扰，该方法的抗干扰能力还有待验证；文献[12]从理论上分析了区内外故障时输电线路无功能量的差异特点，提出了利用区内故障时输电线路两端无功功率极性相反，而区外故障时极性相同的特点实现故障判别；文献[13]结合HVDC输电系统谐波等效电路及其控制策略和典型直流滤波器的幅频特性，利用区内区外故障时两端特征谐波电流的极性差异实现故障判别。

为了克服分布电容电流对保护的影响，文献[14]利用同一低通滤波器来处理线路两侧的电压和电流信号，由于沿线的电压分布在足够低的截至频率范围内呈线性分布，通过积分线性分步电压可以计算出分布电流，然后可将其移除，从而提出利用一个新的差分标准即可实现HVDC输电线路保护；文献[15]研究了基于分布参数模型的HVDC输电线路区内故障和区外故障情况下的不平衡电流，提出了一种采用补偿电流的高压直流输电线路保护算法，在没有传输线传播特性影响的情况下，该方法具有很高的灵敏度；文献[16]利用补偿点处的计算电流来克服现有差动保护存在的保护延时问题，克服了文献[15]方法中传输线传播特性对保护的影响，该方法中涉及的参数可以离线进行预先计算，不受传输线参数的分布、频率相关和耦合特性的影响；文献[17]利用逆变侧的电压电流信号和K-means数据描述KMDD（K-means data description）的方法来检测和分类双极HVDC传输线中的内部故障，该方法能准确识别故障极线，且在实时性检测方面的性能很好，但是并未考虑对区外故障的识别；文献[18]提出一种结合多分辨奇异谱熵和SVM（support vector machine）的HVDC区内外故障识别方法，利用小样本数据识别线路故障，该方法能同时区分整流侧区外故障、区内故障以及逆变侧区外故障，不能实现故障极选择。

由上可知，目前基于智能算法识别HVDC输电线路区内外故障的保护方法较少。Softmax分类器是一种多分类器，能够通过对样本集的训练和测试达到对目标进行多分类的目的。因此，本文提出了一种基于VMD多尺度模糊熵和Softmax分类器的HVDC输电线路故障识别方法，将VMD多尺度模糊熵和VMD能量和比值组成特征向量，利用Softmax分类器对其故障类型进行分类和识别。大量仿真结果表明，该方法可同时实现区内外故障类型识别和故障极选择，具有较强的抗过渡电阻能力和一定的抗干扰能力。

1 相关理论简介

1.1 变分模态分解简介

VMD是一种诞生于2014年的新的非递归、自适应的数据分解方法[19]，分解后所得的各层本征模态函数IMF（intrinsic mode function）包含着丰富的故障信息[20]。变分的数学模型表示为

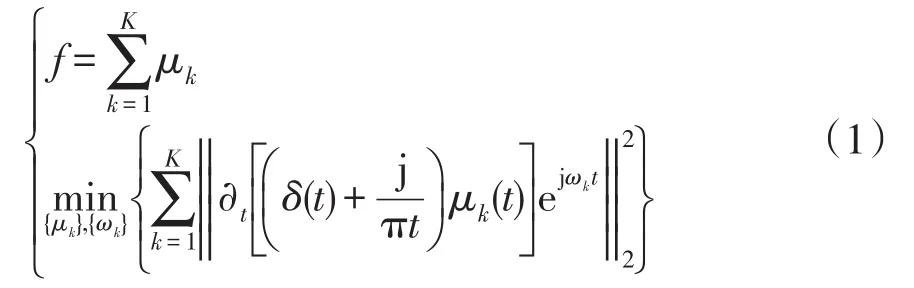
式中：f为待分解的信号；μk为分解得到的第k个模态分量；δ(t)为脉冲函数；j为虚数单位；ωk为第k个模态分量的中心频率。

VMD的分解步骤如下。

步骤3 重复步骤2，直到满足迭代停止条件

1.2 多尺度模糊熵简介

模糊熵用于衡量时间序列在维数变化时所产生新模式概率的大小，概率值越大则模糊熵值越大。如果一个序列的模糊熵值越大，则该信号的复杂度越高[21-22]。模糊熵利用指数函数e-(d/r)n（n和r分别为模糊函数边界的梯度和宽度）作为模糊函数来计算2个时间序列的相似性，其计算过程如下。

（1）对时间序列{u(i):1≤i≤N}进行处理，得到m维向量，即

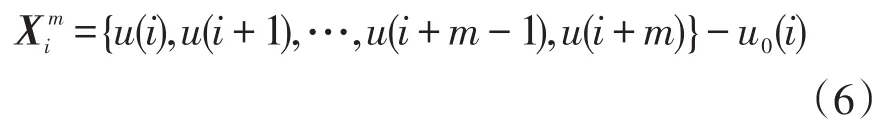
（3）定义函数

（4）根据以上步骤构造m+1向量

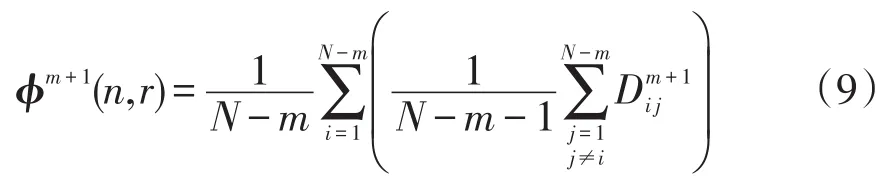
（5）根据以上步骤可得模糊熵值为

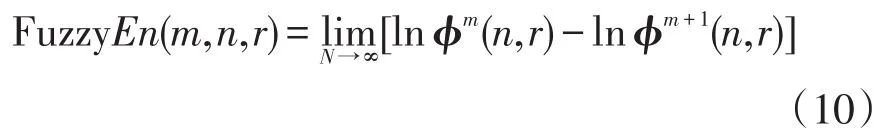
当N有限时，式（10）可变为

由于不同尺度下的故障信号特征频段和复杂程度具有一定的差异性，提取不同尺度下的IMF分量的模糊熵值可以提高结果的准确性，因此对Xi={x1,x2,…,xn}进行粗粒化处理，可形成新的时间序列[23]，即

式中，τ=1,2,…,n为尺度因子。多尺度模糊熵可以表征不同时间尺度下的故障信号的特征，可以有效地解决使用单一模糊熵值衡量时间序列的存在的特征单一问题。利用上述多尺度模糊熵值，组成特征向量 F=(F1F2∙∙∙ Fn)1×n。

2 基于VMD多尺度模糊熵的HVDC输电线路保护原理

2.1 双极HVDC输电系统结构

在PSCAD/EMTDC中建立如图1所示的双极直流输电系统仿真模型。图中:iRP、iRN和iIP、iIN分别为整流侧正负极电流、逆变侧正负极电流，R、I分别表示整流侧和逆变侧，P、N分别表示正极和负极；L表示平波电抗器；DC表示滤波器；L和DC模块组成HVDC输电系统的边界元件；F1～F7为故障点，其中，F1～F2代表整流侧区外正极、负极接地故障，F3～F4代表区内正极、负极接地故障，F5代表两极间短路故障F6～F7代表逆变侧区外正、负极接地故障。本文考虑的输电系统故障主要为单极接地故障和两极间短路故障。保护安装在换流站直流线路内侧，区内以直流线路单极接地故障和两极线路间短路故障为例，区外以平波电抗器外侧单极接地故障为例。模型参考国内某直流输电工程：送电功率3 000 MW，额定电压500 kV，额定电流3 kA，直流滤波器为12/24/36三调谐滤波器，线路模型采用频率相关模型，采用工程上使用的DC2杆塔。设置线路全长1 000 km。

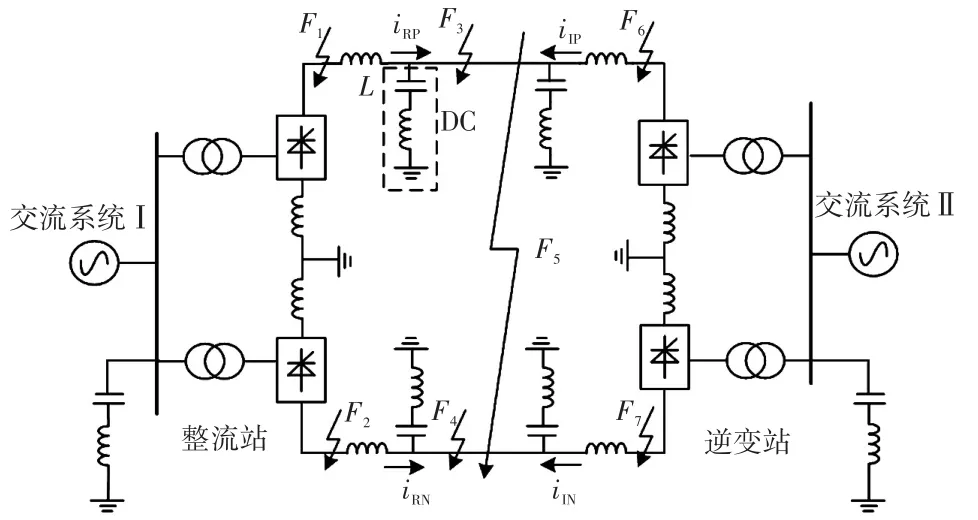
图1 双极HVDC输电系统结构Fig.1 Structure of bipolar HVDC transmission system

2.2 保护原理分析

本文HVDC输电系统模型采用的平波电抗器和直流滤波器构成的实体物理边界DC如图2所示。图中，L=400 mH,L1=39.09 mH,L2=26.06 mH,L3=19.545 mH,L4=34.75 mH,C1=0.9 μF,C2=0.9 μF,C3=1.8 μF,C4=0.675 μF 。由文献[24-25]可知，该直流边界对600、1 200和1 800 Hz的频率信号衰减严重。

图2 边界元件Fig.2 Boundary element

由于VMD分解需预先设定分解模态的个数K，如果预估K值不当，则会导致误差较大，因此本文参考文献[26]使用中心频率法则来预估K值。若出现中心频率相近的模态分量，则认为出现VMD过分解现象[26]。以区内F4点（故障距离400 km，过渡电阻1 Ω）发生故障为例，信号经过VMD分解后，不同K值下各IMF分量的中心频率如表1所示。由表1可知，K＝7时开始出现中心频率相近的IMF分量，即出现过分解现象，因此本文选取分解模态的个数K=6。

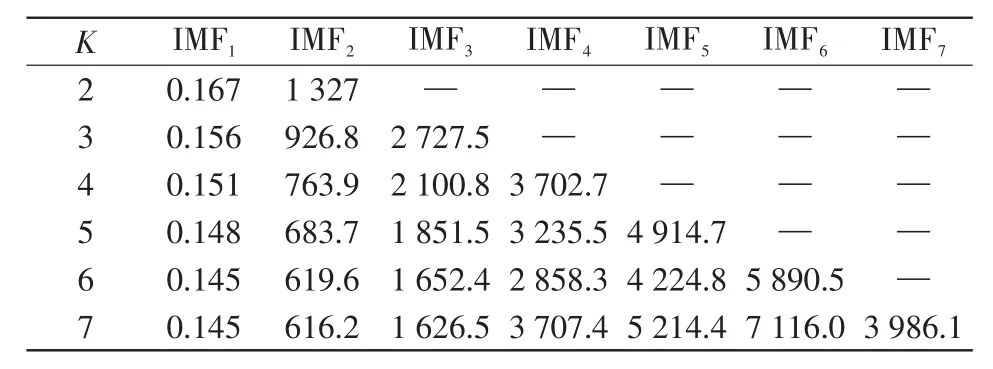
表1 不同K值对应的中心频率Tab.1 Center frequencies corresponding to different K values

由以上分析可知，直流输电线路边界元件对特定频率600、1 200和1 800 Hz的频率信号衰减严重，当发生区内或区外故障时，该特征频率信号呈现的差异明显。同时，当分解模态数为6时，其IMF2分量的中心频率为600 Hz左右，直流输电线路边界元件对该中心频率附近频段的信号具有严重的衰减作用。因此本文选择的IMF2分量构建故障识别特征向量。

2.3 VMD多尺度模糊熵提取分析

由于双极直流输电系统极间耦合的影响，需要对电压电流故障分量进行解耦变换，消除极间耦合的影响。本文利用Karebauer变换对故障电流信号进行解耦变换，以整流侧故障电流信号为例，凯伦贝尔变换解耦公式为

式中：iG、iL分别为地模电流分量和线模电流分量；iRP、iRN分别为整流侧保护安装处测得的正、负极电流。本文选择线模电流分量进行VMD变换，选取合适的本征模态函数IMF2计算VMD多尺度模糊熵。

对整流侧和逆变侧的线模电流iL(t)进行变分模态分解，取两侧的IMF2分量求解多尺度模糊熵，利用两侧的多尺度模糊熵组成特征向量F=(FR1∙∙∙FRnFI1∙∙∙FIn)1×2n，定义该特征向量为信号iL(t)的VMD多尺度模糊熵向量。

当图1所示系统分别于区内正极线F3（1 Ω，500 km）和区外负极F2发生接地故障时，区内故障时整流侧和逆变侧线模电流及其IMF2分量波形如图3所示，区外故障时整流侧和逆变侧线模电流及其IMF2分量波形如图4所示。区内和区外故障时多尺度模糊熵值对比如图5所示。

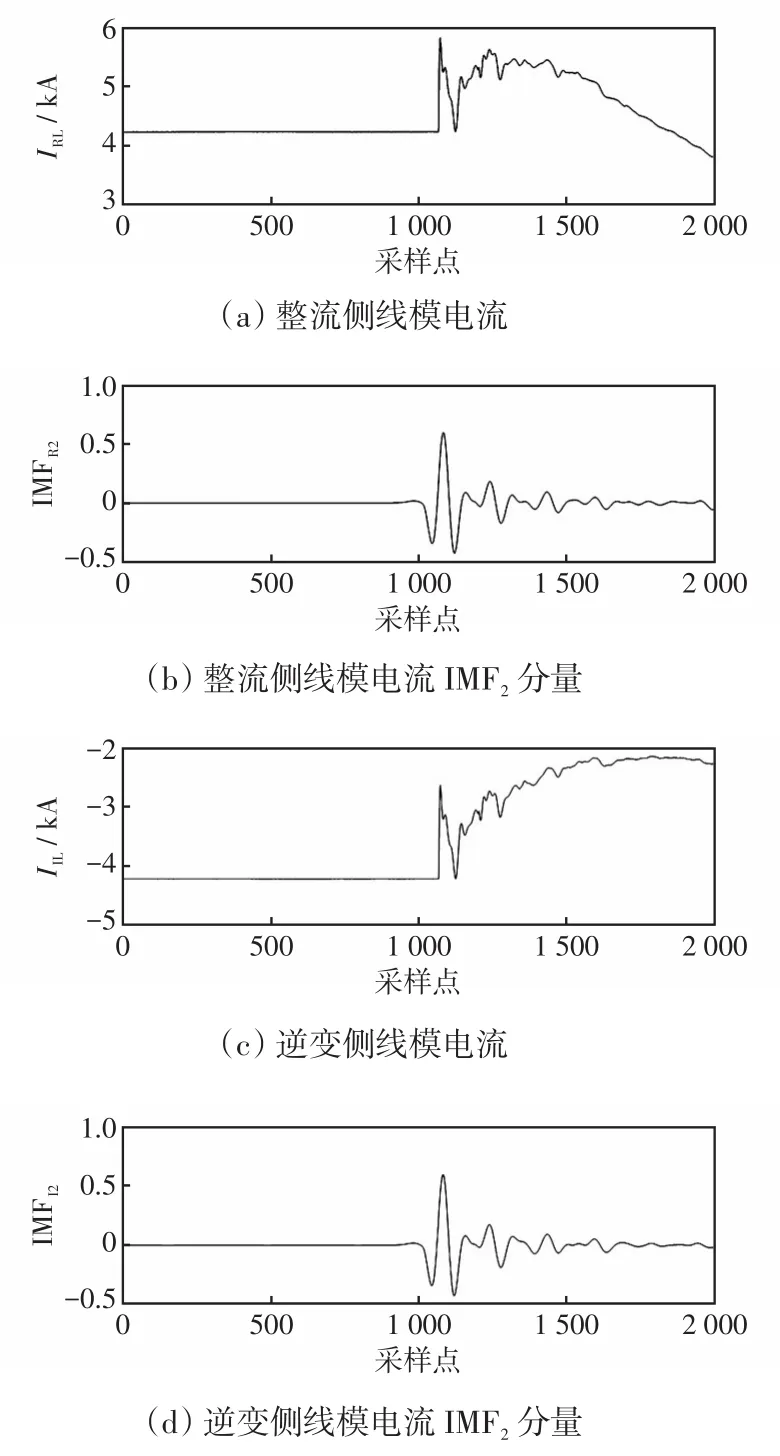
图3 区内故障时相关电流波形Fig.3 Corresponding current waveforms under internal fault

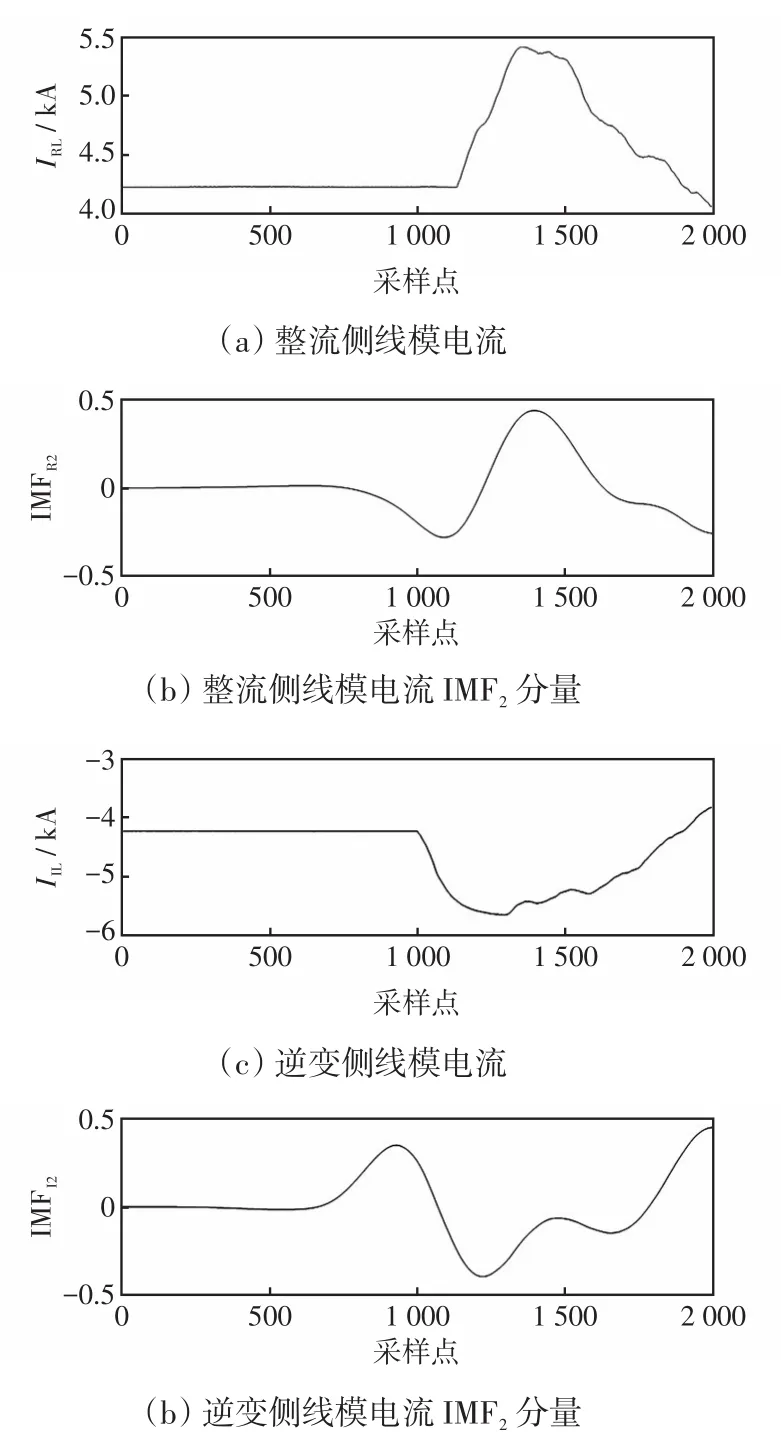
图4 区外故障时相关电流波形Fig.4 Corresponding current waveforms under external fault

结合第2.2节的分析和图3～图5可知，区内故障时IMF2分量在输电线路上衰减程度较小，故障暂态分量较多，此时的模糊熵值较大。而区外故障时暂态电流信号经边界元件的衰减后到达保护安装处，此时IMF2分量衰减程度较大，故障暂态分量较少，因此模糊熵值较小。

图5 区内外故障时多尺度模糊熵对比Fig.5 Contrast of multi-scale fuzzy entropy under internal and external faults

由图5可知，在一定的变换尺度内，随着变换尺度的增加，区内故障时的模糊熵值均大于区外故障时的模糊熵值，差异明显，而随着变换尺度的继续增加，区内外模糊熵值的差异减小。因此，为了能够很好地反映区内外故障特征差异，本文选择的多尺度模糊熵变换尺度为10。

2.4 VMD能量之和比值特征提取

双极直流输电系统中，由于双极线路之间的电磁耦合效应，当某一极发生故障时，非故障极也会产生较大的电磁暂态量。为了防止非故障极保护装置误动作，需要准确识别故障极。本文提出利用两极线路暂态电流VMD能量之和的比值来表征故障极特征，对整流侧和逆变侧的正负极电流分别进行VMD变换，将IMF2分量均分为m段，分别求取每一段采样数据的能量之和的比值，即

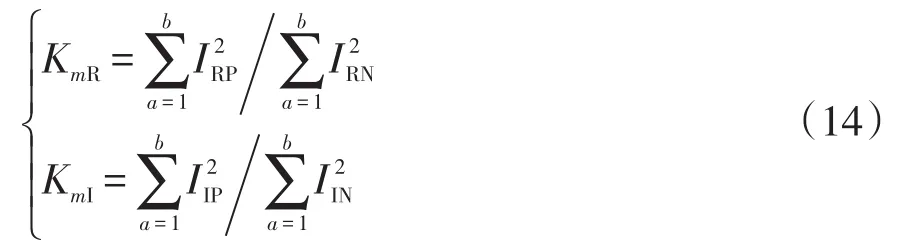
式中：m为IMF2分量的第m段；IRP和IRN分别为整流侧正极线路和负极线路电流信号VMD变换后的IMF2分量的第m段信号；a=1表示第m段采样数据的第1个采样点；b为第m段采样数据窗内的采样点数。

利用正负极故障电流信号的能量和比值构建故障极识别特征向量 K=(KR1∙∙∙KRmKI1∙∙∙KIm)1×2m，定义该向量为VMD能量之和比值向量。

3 Softmax分类器

Softmax分类器是Logistic回归在多分类问题上的扩展，当分类数为2时，则为Logistic分类，当分类数大于2时，则应用于解决多分类问题。Softmax函数实际上是有限项离散概率分布的梯度对数归一化。它能将一个含任意实数的K维向量Z“压缩”到另一个K维实向量σ(z)中，使得每一个元素的范围都在（0，1）之间，并且所有元素的和为1[27]。

Softmax分类器的定义为 hλ(vi)[27]，表示为

式中：p(ci=r|vi;λ)为特征向量 vi被识别为第k（k=1,2,…,r）类的概率，p(ci=r|vi;λ)为一个r行1列的列向量，每行表示当前特征向量被识别为第k类的概率，所有行元素的和为1；λk为Softmax分类器待估计的参数，并且构成参数矩阵λ。

对于vi，选择最大概率取值对应的k作为当前故障类型的分类结果，并与故障类型的真实分类作比较。如果一致，则分类正确；否则，分类错误。代价函数 J(λ)定义为

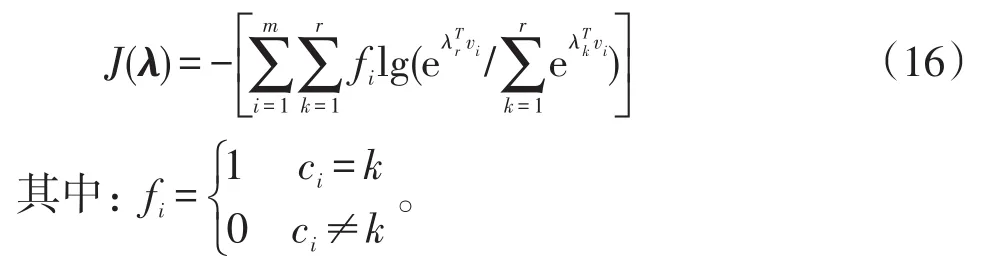
采用共轭梯度算法求解J(λ)无约束最优化问题，以测试集分类正确率作为分类方法性能评价指标。

为了用同一网络实现区内外故障判断和故障极判断，本文采用能同时反映区内外故障特征和故障极特征的组合特征向量 θ=(F,K)=(FR1∙∙∙FRnFI1∙∙∙FInKR1∙∙∙KRmKI1∙∙∙KIm)1×2(n+m)作 为 Softmax分类器的输入向量，分类及标签号如表2所示。针对本文特征向量 θ1×2(n+m)，共含有2（m+n）个特征量，需判断该特征向量属于5类中的哪一类，因此，Softmax分类器分类原理如图6所示。当Pmax=Ph(h=1,2,3,4,5)，则该特征向量属于第h类。

图6 Softmax分类器Fig.6 Softmax classifier

表2 Softmax分类器分类标签Tab.2 Classification labels of Softmax classifier

E代表线路区外，L表示线路区内，G表示接地故障。对于h种独立分类，设置输出个数为h，对应的分类标签号依次为1,2,∙∙∙,h，每个标签号对应一个输出分类。本文研究的故障类型可分为5类，分别为：区外正极接地故障、区外负极接地故障、区内正极接地故障、区内负极接地故障和区内正负极间故障，设置输出类型为5种，对应标签号为1～5。

4 基于VMD多尺度模糊熵和Softmax分类器的HVDC输电线路智能故障识别方法

智能故障识别算法流程实现步骤如下。

步骤1 VMD多尺度模糊熵特征提取。

（1）对测量点处测得的电流信号进行凯伦贝尔极模变换；

（2）取线模量分析进行变分模态分解；

（3）取故障后3 ms时间窗内采样数据；

（4）选取VMD本征模特函数IMF2求取多尺度模糊熵，利用VMD多尺度模糊熵构造区内外故障识别特征向量 F=(FR1∙∙∙FRnFI1∙∙∙FIn)1×2n。

步骤2 VMD能量和比值特征提取。

（1）对测量点处测得的正负极电流信号进行变分模态分解；

（2）获取故障后3 ms时间窗内采样数据；

（3）将VMD本征模特函数IMF2均分为m段，求取每段分量的能量和比值，利用VMD能量和比值构 建 故 障 极 识 别 特 征 向 量 K=(KR1∙∙∙KRmKI1∙∙∙KIm)1×2m。

步骤3 将VMD多尺度模糊熵特征向量F=(FR1∙∙∙FRnFI1∙∙∙FIn)1×2n和 VMD 能量和比值特征向量 K=(KR1∙∙∙KRmKI1∙∙∙KIm)1×2m组合，形成能同时反映区内外故障特征和故障极特征的组合特征向量θ =(F,K)=(FR1∙∙∙FRnFI1∙∙∙FInKR1∙∙∙KRmKI1∙∙∙KIm)1×2(n+m)，以此表征HVDC输电线路故障特征。

步骤4 为每个样本向量进行标号后作为故障特征样本数据，将训练样本输入Softmax分类器进行训练，得到基于Softmax分类器的HVDC输电线路智能故障识别模型。将测试样本输入训练好的Softmax分类器中，得到识别结果。故障别算法流程如图7所示。

图7 故障识别算法流程Fig.7 Flow chart of fault recognition algorithm

5 仿真实验

5.1 建立基于Softmax分类器的智能故障识别模型

训练样本由HVDC输电系统发生不同故障时采样数据不受噪声干扰和采样数据受噪声干扰两部分组成。本文考虑的区内故障包括正极接地故障（LPG）、负极接地故障（LNG）和正负极间短路故障（LPN）共3种情况，考虑故障距离（距整流侧保护安装处）分别为1、100、200、300、400、500、600、700、800、900、999 km共11种情况，考虑过渡电阻分别为1、10、100、200、300、400、500、600 Ω共8种情况，因此区内不受噪声干扰数据样本共3×11×8=264个。考虑的区外故障情况包括整流侧正、负极接地故障（RPG、RNG），逆变侧正、负极接地故障（IPG、ING）共4种情况，过渡电阻取法和区内一致，因此区外不受噪声干扰数据样本共4×8=32个。区外噪声干扰数据样本取法和区外无噪声干扰数据样本保持一致，也是4×8=32个。因此本文的训练样本总数为3×11×8+4×8+4×8=328个。

将训练样本输入到Softmax分类器网络中进行训练，得到基于Softmax分类器的智能故障识别模型，将不同于训练样本的测试样本数据输入到该智能故障识别模型中，即可得到识别结果。

5.2 训练样本识别结果分析

把故障特征训练样本输入Softmax分类器网络中进行训练，得到一个训练好的基于Softmax分类器的HVDC输电线路智能故障识别模型。训练集的混淆矩阵如图8所示，横轴表示标签号，纵轴表示输出标签号。网络默认最大迭代次数为1 000，当迭代次数达到657时，训练样本的测试结果正确率达到100%，此时智能故障识别模型能很好地识别HVDC输电线路故障。

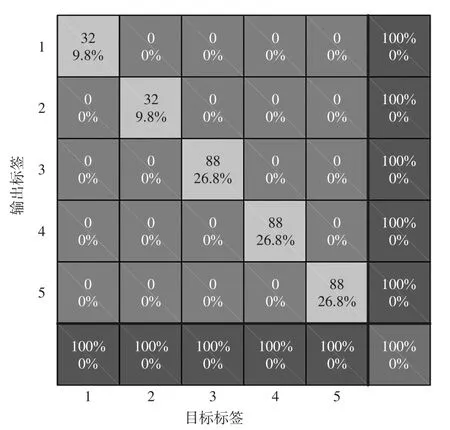
图8 混淆矩阵Fig.8 Confusion matrix

5.2.1 发生不同故障类型时测试结果分析

为验证保护算法对不同类型故障的适应性，分别选取图1所示系统整流侧区外正极F1、负极F2点故障，输电线路F3、F4和F5故障，逆变侧区外正极F6、负极F7故障共7种情况进行测试。在相同故障距离和过渡电阻的情况下，针对不同类型故障构建测试样本集，并输入训练好的Softmax分类器模型进行测试，测试结果对比如图9所示，表3为对应故障情况的仿真验证结果。

图9 不同类型故障时的测试结果对比Fig.9 Comparison among test results under different types of fault

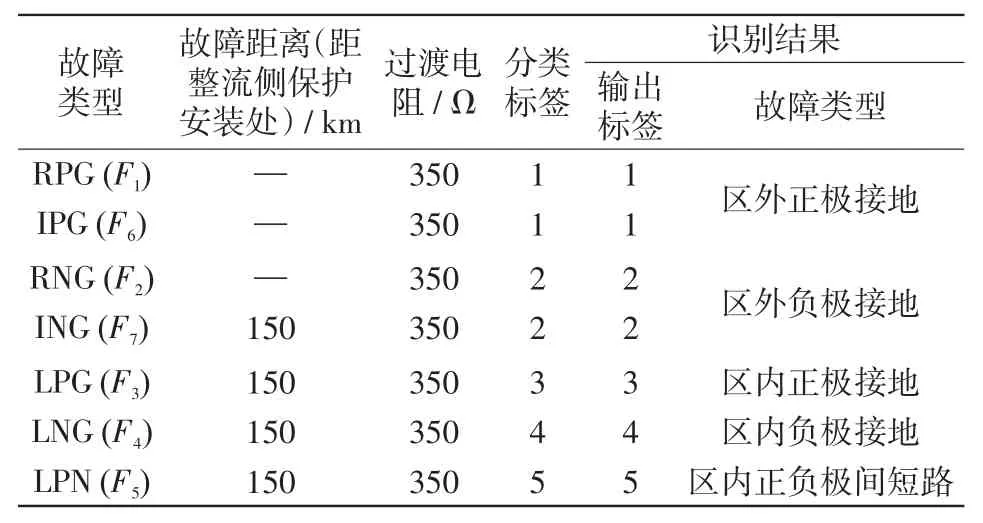
表3 不同类型故障仿真验证结果Tab.3 Simulation verification results under different types of fault

表3和图9表明，该故障识别模型不受HVDC输电线路故障类型的影响，能够实现准确的区内外故障识别和故障选极。

5.2.2 发生不同过渡电阻故障时测试结果分析

为验证不同过渡电阻故障，特别是线路发生远端高阻故障时保护算法的性能，分别设置图1所示系统整流侧区外正极F1点，输电线路F3、F4和F5，逆变侧区外负极F7在不同过渡电阻条件下发生故障，选取15个测试样本构建测试样本集，输入训练好的Softmax分类器模型进行测试，测试结果对比如图10所示，表4为对应故障情况的仿真验证结果。

由表4和图10表明，在不同过渡电阻情况下，该模型能够进行准确地区内外故障识别和故障选极，耐受过渡电阻能力强，特别是在输电线路远端高阻故障情况下也能进行准确识别和选极。

表4 不同过渡电阻情况下的仿真验证结果Tab.4 Simulation verification results under different transition resistances

图10 不同过渡电阻情况下的测试结果对比Fig.10 Comparison among test results under different transition resistances

5.2.3 发生不同距离故障时测试结果对比分析

为了验证不同故障距离情况下保护算法的性能，分别设置图1所示系统正极F3、负极F4和两极F5点在不同距离情况下发生故障，选取15个样本构建测试样本集，输入训练好的Softmax分类器模型进行测试，测试结果对比如图11所示，表5为对应故障情况的仿真验证结果。

表5和图11表明，该故障识别模型不受故障距离的影响，在不同故障距离情况下能实现准确的故障识别和故障选极。

由表3～表5和图9～图11可知，在故障后3 ms内，基于VMD多尺度模糊熵和Softmax分类器的HVDC输电线路智能故障识别模型不受故障类型和故障距离的影响，利用同一网络能有效识别HVDC输电线路区内外故障并进行故障选极，耐受过渡电阻能力强。

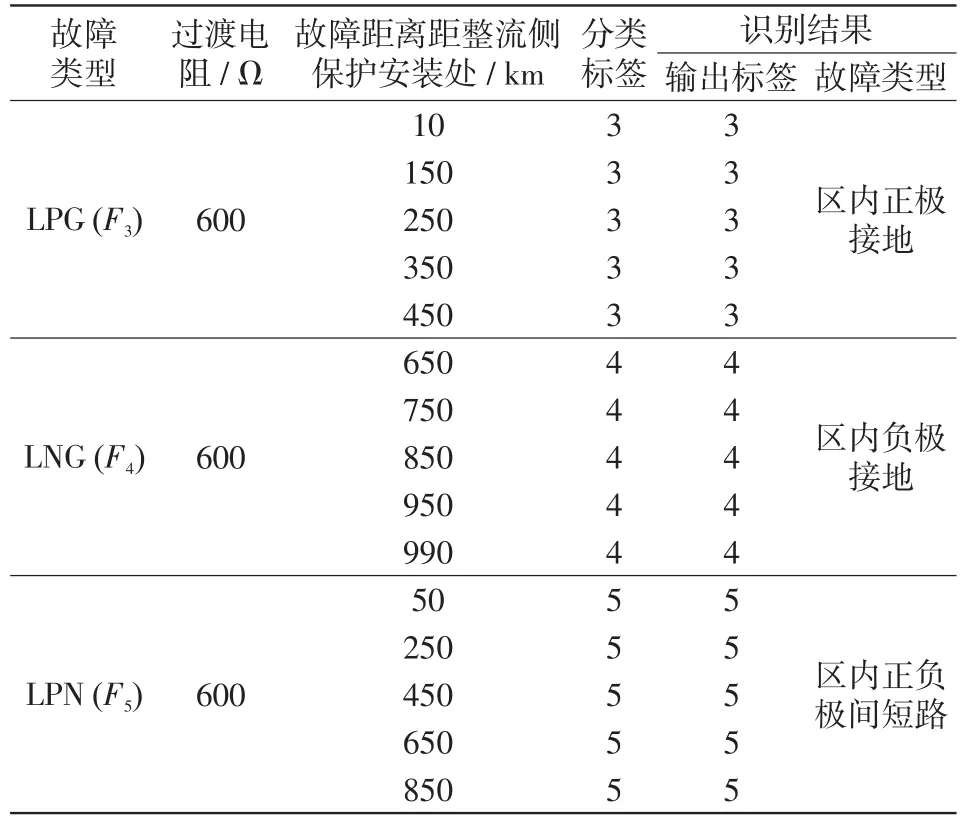
表5 不同故障距离情况下的仿真验证结果Tab.5 Simulation verification results under different fault distances

图11 不同距离故障下的测试结果对比Fig.11 Comparison among test results under different fault distances

5.3 算法性能分析

为了验证在噪声影响情况下保护算法的性能，选取图1所示系统逆变侧区外正极F6故障，输电线路F3、F4和F5故障，整流侧区外负极F2故障共5种故障情况进行仿真，噪声干扰分别考虑SNRs=50、60、70 dB共3种情况，得到 5×3=15组噪声干扰测试样本。图12所示为区内正极F3故障（过渡电阻10 Ω，F3距整流侧保护安装处400 km）和区外负极F7（过渡电阻10 Ω）故障且存在50 dB噪声干扰时的相关波形。

图12 存在50 dB噪声干扰时的相关波形Fig.12 Corresponding waveforms under 50 dB noise interference

将上述15组噪声干扰测试样本输入基于Soft⁃max分类器的智能故障识别模型中进行测试，测试结果对比如图13所示，表6为对应故障情况的仿真验证结果。

从表6和图13可以看出，该智能故障识别模型在远端高阻故障且受噪声干扰时仍能实现故障判别，即使在信噪比为50 dB时也能可靠识别区内外故障，同时实现故障选极。因此，本文所提算法受噪声的影响较小，具有一定的抗噪能力。

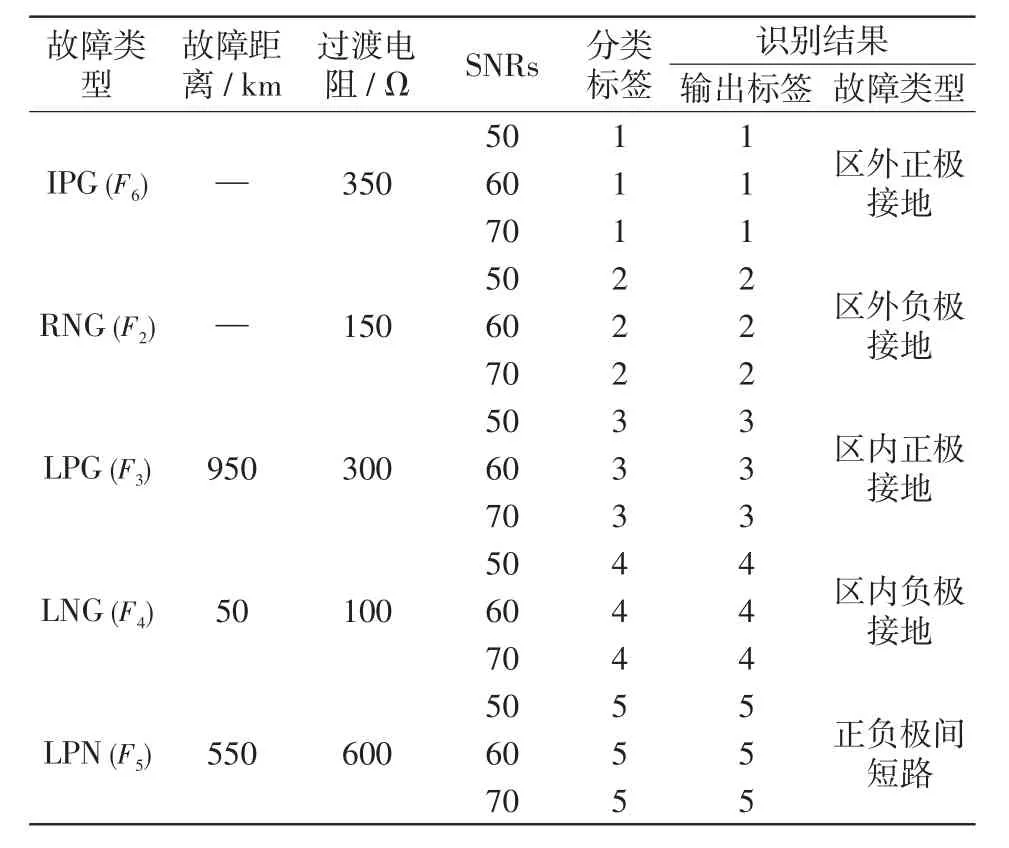
表6 噪声干扰情况下保护算法性能分析Tab.6 Performance analysis of the protection algorithm under noise interference

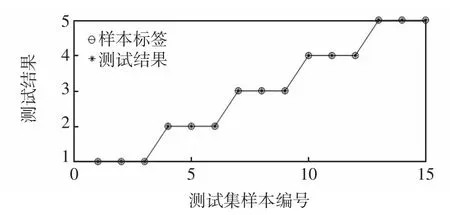
图13 50～70 dB噪声干扰测试结果对比Fig.13 Comparison among test results under 50—70 dB noise interference

5.4 与其他网络对比

为了验证本文模型的识别效果，分别选取BP、ELM和RBF网络对本文讨论的HVDC输电线路故障进行诊断识别，并和本文利用Softmax分类器得到的结果进行比较，得到的测试结果对比如表7所示。由表7可知，利用Softmax分类器的HVDC输电线路故障识别模型的正确识别率比另外3种智能识别模型的准确识别率更高。这表明本文所提方法的模型具有更好的识别率和更为优越性能，可以有效解决HVDC输电线路的故障识别问题。

表7 识别结果对比Tab.7 Comparison among recognition results

6 结语

本文利用HVDC输电线路边界对信号的衰减作用，提出基于VMD多尺度模糊熵和Softmax分类器的HVDC输电线路智能故障识别方法。该方法通过变分模态分解提取中心频率为600 Hz左右的IMF2分量，对IMF2分量求解故障后3 ms内的VMD多尺度模糊熵向量和VMD能量和比值向量，构建故障特征样本集，对建立的基于Softmax分类器的智能故障识别模型进行训练和测试，实现HDVC输电线路内外故障识别和故障选极。理论推导和仿真实验结果表明：本文利用VMD多尺度模糊熵反映区内外故障特征，利用VMD能量和比值反映故障极特征，利用组合特征向量作为基于Softmax分类器的智能故障识别模型的输入，使用一个智能网络就能同时实现线路区内外故障识别和故障极选择，克服了传统保护需要不同判据才能实现区内外故障识别和故障选极且阈值整定困难等缺点；利用Softmax分类器将HVDC输电线路区内外故障识别和故障极选择问题转化为模式识别问题，通过训练得到合适的Softmax分类器参数即可同时实现区内外故障识别和故障选极。在整个分类过程中可实现自动化，同时，该方法耐受过渡电阻能力强，具有一定的抗干扰能力。该方法的不足之处在于其抗噪能力还有待提高，和VSC-HVDC相比，在很大程度上依赖于边界元件对特征频率信号的阻滞作用，因此，此方案的有效性不考虑VSC-HVDC系统。