考虑分布式电源相关性的配电网概率潮流计算
2021-06-10许加柱贾龙涛王岐珂
许加柱,贾龙涛,李 畅,王岐珂
(国家电能变换与控制工程技术研究中心(湖南大学),长沙 410082)
分布式电源是现有发电模式的一种补充,目前大量分布式电源接入交流配电网。然而,分布式电源的波动性和随机性会给配电网带来不确定性因素,影响配电网的潮流分布和安全运行。相比确定性潮流,概率潮流PLF(probabilistic load flow)能分析不确定性因素对配电网运行的影响。PLF由Borkowska于1974年提出[1],此后国内外开展了大量研究,取得丰富成果。现在PLF主要用于电力系统优化调度[2]、规划设计[3]、风险评估[4]等方面。依据原理,概率潮流计算方法可以分为模拟法[5-6]、近似法[7-8]、解析法[9-10]。其中,模拟法是一种依托大数定律的试验统计方法,虽然可以很精确地获取节点电压和支路潮流的概率特征,但运算时间很长,一般作为评价其他算法的标准;近似法依据输入变量的概率特性近似描述输出变量的概率特性,包括点估计法、一次二阶距法等方法;解析法依据输入变量、输出变量之间的线性关系进行计算,主要有卷积法和半不变量法,其中半不变量法需要满足输入变量相互独立[11]。
文献[2]计及分布式电源和负荷的不确定性,利用半不变量法计算概率潮流,达到实时调整日前调度计划的目的。在低压配电网接入大量小型分布式光伏的情况下,文献[7]使用蒙特卡洛法和点估计法分别计算配电网的电气特征,并将两种方法进行对比。配电网的供电半径一般不超过15 km,在此区域内光照强度、云况基本相似,受此影响,该区域内多个分布式光伏具有相似的出力特性,其出力波动趋势基本一致,具有一定的相关性[15]。根据大量统计数据,不同种类的分布式电源出力也具有一定的相关性,若该相关性被忽略,则计算结果的可信度大打折扣。上述一些文献没有充分考虑分布式电源出力的相关性。针对上述问题,一些文献考虑了分布式电源出力的相关性。文献[12]采用Cho⁃lesky分解探究相邻地区光伏出力和负荷之间的相关性;文献[13]采用Nataf变换来构建风力发电场景,研究风速相关性对PLF的影响;文献[14]指出,在基于广义多项式混沌法的PLF计算中,若将Nataf变换应用其中处理不确定性变量之间的相关性,可能会低估极端事件发生的概率,因此该文献提出采用数据驱动任意多项式混沌法解决该问题;文献[15]考虑天气变化的影响,计及分布式光伏多点接入,提出一种基于等效功率相关系数的方法计算PLF,用以评估配电网的运行风险。
尽管上述方法研究了分布式电源的相关性,但是鲜有文献考虑风电出力与光伏出力的负相关性,针对于此,本文充分考虑了风电出力之间、风电出力和光伏出力之间的相关性,提出一种基于Rosen⁃blatt逆变换和半不变量法RITCM(Rosenblatt in⁃verse transformation and cumulant method)的概率潮流计算方法。该方法使用金融领域广泛应用的Copula函数来描述分布式电源出力的相关性,并建立联合分布函数;对具有相关性的出力样本进行Rosenblatt逆变换,使之相互独立,进而采用半不变量法结合Cornish-Fisher级数展开计算节点电压、支路潮流的概率分布;最后,在34节点系统上对RITCM进行验证,计算了相对误差和希尔不等系数两个指标,并通过与蒙特卡洛法比较,验证了RITCM在考虑分布式电源出力相关性的配电网概率潮流计算方面的有效性和正确性。
1 相关变量的独立化变换
1.1 基于Copula函数的联合分布函数
变量之间的相关性可以用Pearson相关系数来度量,其概念清晰,但适用范围有限。Pearson相关系数要求随机变量必须具有标准差,但有些特殊函数无法满足该要求;此外当变量间的关系是非线性时,用Pearson相关系数来度量其关系并不可靠,因此需要选用一种更加科学的方法。Copula函数能够描述变量间的非线性相关性,同时易于构建联合分布模型,在金融领域有着广泛的应用,本文引入Copula函数描述分布式电源出力的相关性。
Sklar于1959年提出Copula函数,该函数描述了一个N维变量的联合分布函数与各变量边缘累积分布函数之间的关系,Copula函数的密度函数则描述了N维变量的联合概率密度函数和各变量密度函数之间的关系,其基本理论是Sklar定理。以二维随机变量为例加以说明,由Sklar定理易知,存在Copula函数C满足

式中:F1(x1)、F2(x2)分别为随机变量x1、x2的累积分布函数;F(x1,x2)为x1、x2的联合分布函数。若F1(x1)、F2(x2)连续,则C唯一确定。
Copula函数主要有二元Normal Copula函数、二元t-Copula函数、Gumbel Copula函数、Clayton Copu⁃la函数、Frank Copula函数[16],其中前2种为椭圆Copula函数,后3种为阿基米德Copula函数,不同的函数描述不同类型的相关性。常用的Copula函数相关性测度有Kendall秩相关系数τ及Spearman秩相关系数ρ。τ和ρ可以描述随机变量的变化方向是否一致,值为0表示随机变量不存在相关性,值为正表示存在正相关,值为负表示存在负相关,且值的绝对值越接近1,表明相关性越强。
基于Copula函数建立联合分布模型一般需要2步:首先确定分布式电源出力的边缘分布函数,再选取适当的Copula函数建立联合分布模型。Copu⁃la函数可以描述随机变量间的相关性,但是无法实现相关变量的独立化变换。
1.2 基于Rosenblatt逆变换的独立化变换
由于分布式电源出力存在相关性,无法直接使用半不变量法计算PLF,因此必须首先对具有相关性的分布式电源出力进行独立化变换。
相关变量的独立化变换在结构可靠度分析中有广泛的应用,主要有以下4种方法:Orthogonal变换、Nataf变换[13]、Winterstein近似公式和Rosenblatt变换。其中,Orthogonal变换步骤简单,不受变量类型的限制,但只有当变量服从正态分布或者相互独立时,其精度才较高;与Orthogonal变换相比,Nataf变换考虑了变换前后等效相关系数的变化,导致Nataf变换的计算过程更加复杂,此外,当样本分布类型或变量联合分布函数不满足高斯分布时,其误差可能较大;Winterstein近似公式的计算精度受变量统计矩的估计精度影响较大,尤其是偏度和峰度;Rosenblatt变换的原理是利用变量的边缘概率密度和条件概率密度进行变换,该方法可以准确描述变量间的相关性,且不受变量的分布类型、变量间是否具有线性相关性的影响,变换结果精确,本文采用该方法对分布式电源出力进行独立化变换。
假设 f(x1,x2)是分布式电源出力的联合概率密度函数,其可以表示为
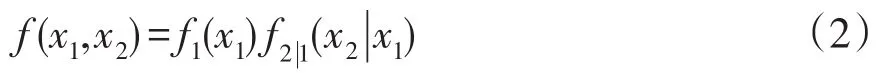
式中:f1(x1)为x1的概率密度函数;f2|1(x2|x1)为x2在x1条件下的概率密度。
由式(2)可推得

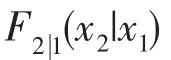
依据等概率变换原则,Rosenblatt变换可以将非正态相关变量变换成独立的标准正态变量。等概率变换原则可以表示为

式中,ui、Φ(ui)分别为标准正态变量及其累积分布函数,其中i=1,2。
Rosenblatt逆变换可以将标准正态变量变换成分布式电源出力的独立样本,详细步骤如下。
步骤1 产生n个服从标准正态分布函数U1、U2的样本。
步骤2 依据式(4),得

由式(5)可以求得其中一个分布式电源出力X1的n个样本。
步骤3 依据式(4),得

由式(6)可以求得另一个分布式电源出力X2的n个样本。
2 基于半不变量法的潮流计算
第1节求得相互独立的分布式电源出力样本,本节采用半不变量法计算PLF。
半不变量是随机变量的一种特征,依据独立化变换后分布式电源出力的样本,分别计算各阶原点矩,再依据半不变量和原点矩的关系求得独立化变换后分布式电源出力的各阶半不变量。视负荷的有功功率、无功功率服从正态分布,其一阶、二阶半不变量分别为期望和方差,三阶及其以上高阶半不变量均为0。基于半不变量法的潮流计算的基本思想为:依据系统初始条件计算一次确定性潮流,并将计算结果作为基准点,在此基础上叠加用半不变量描述的分布式电源、负荷等的扰动,计算系统状态变量的半不变量,最后结合级数展开得到状态变量的概率分布。
在交流潮流模型下,在基准点处对潮流方程进行泰勒展开,忽略二次项及其高次项,可得

式中:W为节点注入功率;X、Z为状态变量,分别表示节点电压和支路潮流,ΔW、ΔX、ΔZ分别为W、X、Z的扰动;J0为雅可比矩阵;G0为灵敏度矩阵。
式(7)可进一步表示为

对于高阶半不变量,式(8)表示为

目前在电力系统中常用的级数展开主要有Gram-Charlier级数、Edgeworth级数和Cornish-Fisher级数,当随机变量是非正态分布时,与前两种级数相比,Cornish-Fisher级数在计算概率分布时具有更高的精度,因此本文采用8阶Cornish-Fisher级数展开逼近输出变量的分布函数。
考虑分布式电源出力相关性的配电网概率潮流计算方法的流程如图1所示。

图1 考虑相关性的配电网概率潮流计算流程Fig.1 Flow chart of PLF calculation for distribution network considering correlation
3 算例分析
在某34节点系统上对RITCM的准确性和快速性进行验证,其中节点15和节点34分别接入分布式电源,如图2所示。本文仿真2种情况,分别是接入同一配电网的2台风电(风电/风电)出力的相关性、风电与光伏(风电/光伏)出力的相关性,风电、光伏的额定功率均为0.4 MW。仿真所使用的计算机参数主要有:处理器为Intel(R)Core(TM)i7-7700 CPU@3.60 GHz,运行内存8 GB,仿真软件是Matlab R2016a。

图2 含分布式电源的34节点系统Fig.2 34-node system with distributed generations
采集某地2台风电和一座光伏的出力数据,在研究风电出力与光伏出力的相关性时舍弃值为0的光伏出力及其相对应同时刻的风电出力数据。本文假设风电、光伏均以恒定功率因数0.9(滞后)运行。
表1给出了2种情况下5种Copula函数的Ken⁃dall秩相关系数τ和Spearman秩相关系数ρ的值。从表1可以看出,风电/风电出力的τ和ρ均为正值且接近1,表明风电出力具有较强的正相关性;风电/光伏出力的τ和ρ与Copula函数的种类相关,一部分是绝对值较小的负数,另一部分是接近于0的数,表明风电/光伏出力具有较弱的负相关性。此外,计算了原始样本的秩相关系数,风电/风电出力的τ和ρ分别为0.864 5和0.976 1,风电/光伏出力的τ和ρ分别为-0.268 9和-0.377 6,综合考虑决定采用Frank Copula函数描述分布式电源出力的相关性,并建立联合分布函数。
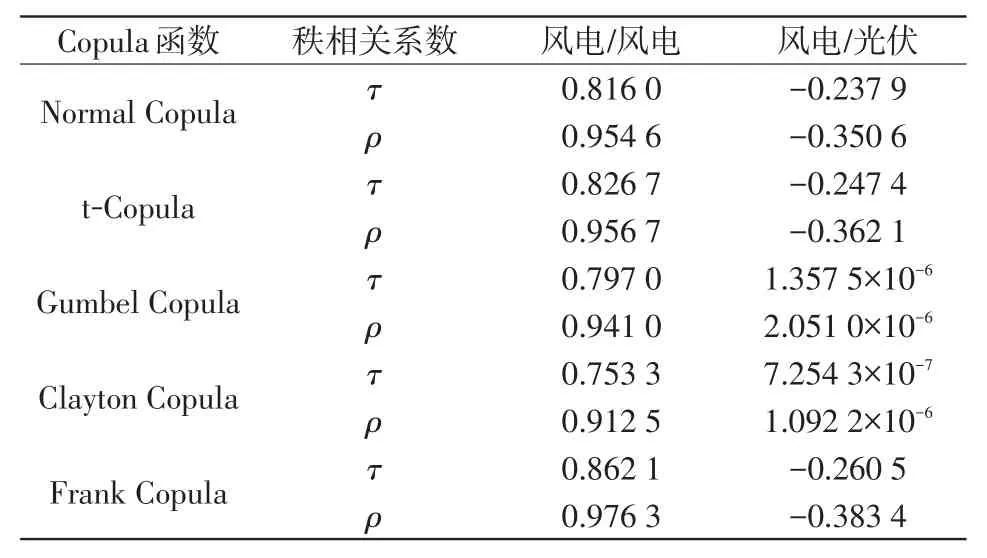
表1 2种情况的秩相关系数Tab.1 Rank correlation coefficients in two cases
经过Rosenblatt逆变换将相关的分布式电源出力进行独立化变换,生成不相关样本。经过计算,变换后风电/风电出力的秩相关系数τ和ρ分别为0.010 1和0.014 5,风电/光伏的秩相关系数τ和ρ分别为0.025 3和0.038 5,结果表明,变换后分布式电源出力的相关性大大降低,可以视为相互独立。
仿真设置了蒙特卡洛模拟MCS(Monte Carlo simulation)法、RITCM两种方法计算PLF。为体现相关性,MCS法使用独立化变换前具有相关性的风电/风电、风电/光伏出力数据,且只对其中一种出力数据进行随机采样,另一种出力为同时刻的数据。综合考虑仿真精度和计算时间,MCS法设置10 000次随机抽样,进行确定性潮流计算,得到节点电压、支路潮流的概率分布,并以此为标准评价RITCM的准确性和有效性。Rosenblatt逆变换后的独立样本采用半不变量法计算节点电压、支路潮流的概率分布。
在风电/光伏相关性情况下,图3为使用MCS和RITCM两种方法计算得到的节点34和节点8的电压幅值概率分布,图4为使用MCS和RITCM两种方法计算得到的支路24-27的有功功率和无功功率概率分布。从图3和图4中可以看出,2种方法得到的节点电压幅值、支路潮流的概率分布基本重合,相差较小。
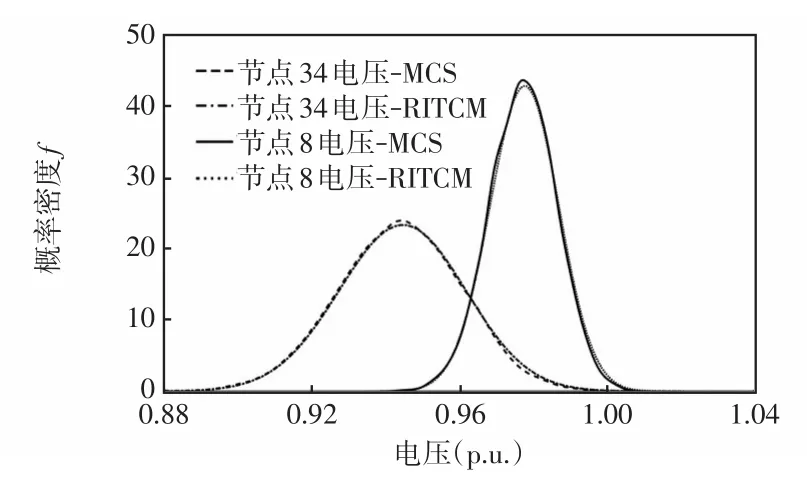
图3 2种方法计算节点8和34的电压幅值概率分布Fig.3 Probability distributions of voltage amplitude at Nodes 8 and 34 calculated using two methods
图3只反映了风电/光伏相关性情况下某些节点电压幅值的概率分布,图4只反映了上述情况下某条支路潮流的概率分布,整个仿真模型有34个节点和33条节点间的支路,要想通过绘图得到每个节点的电压幅值概率分布和每条支路的潮流概率分布,进而全面评价RITCM的准确性,显然不现实。因此本文采用相对误差和希尔不等系数TIC(Theil inequality coefficient)作为定量指标,将误差量化。相对误差包含节点电压幅值、支路潮流的期望值、标准差的相对误差,主要用来度量所提方法输出变量在统计方面的准确性;TIC可以定量评价计算方法的预测精度,TIC的值介于0~1之间,值越小表明预测值越接近于真实值,即预测精度越高。计算公式分别为

图4 2种方法计算支路24-27的功率概率分布Fig.4 Power probability distribution of branch 24-27 calculated using two methods

以风电/光伏相关性为例分析PLF的计算结果。表2为除节点1外的其余节点电压幅值的期望值、标准差的相对误差和TIC,表3和表4分别为各支路有功功率、各支路无功功率的期望值、标准差的相对误差和TIC,各指标的平均值也可以从相应表中得到。分析相对误差数据可以发现,RITCM计算得到的输出变量的期望与MCS得到的结果非常接近,相对误差小;相对而言,RITCM在处理输出变量标准差方面的准确性有待提高。分析TIC数据可以发现,RITCM具有较高的预测精度。
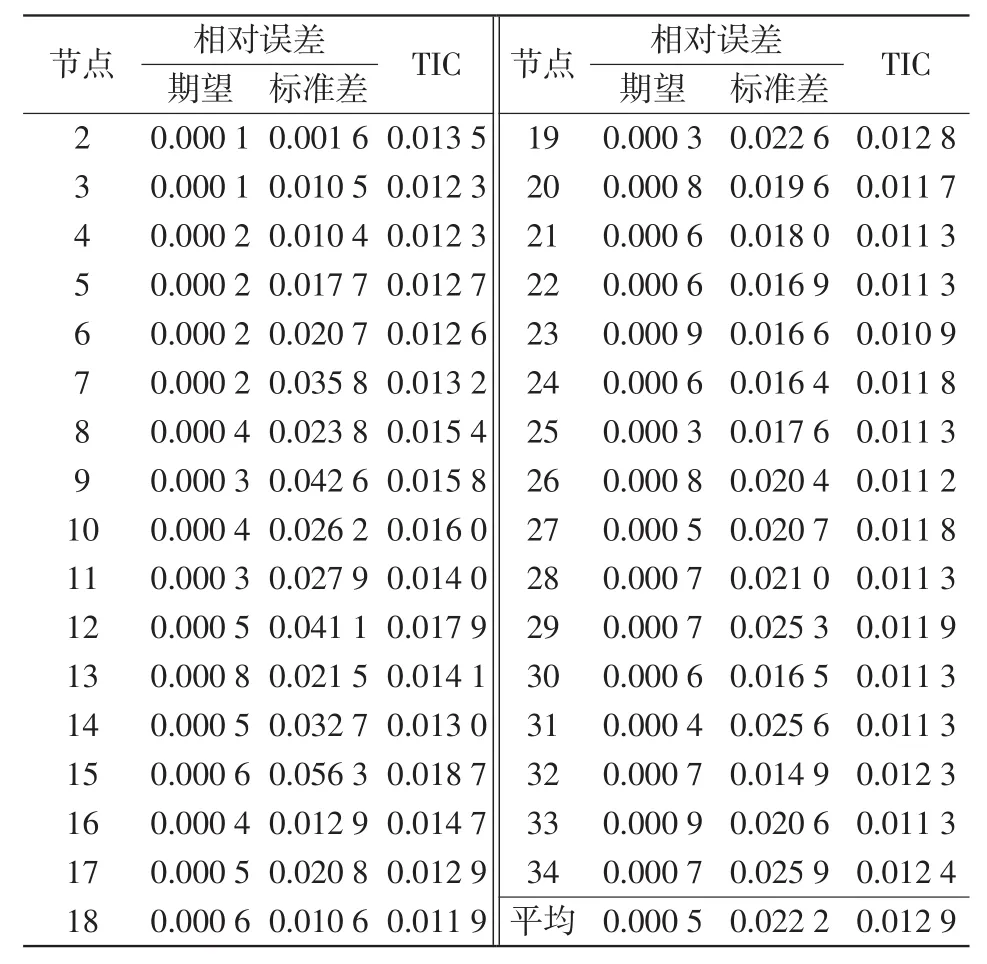
表2 节点电压幅值的相对误差和TICTab.2 Relative error and TIC of node voltage amplitudes

表3 支路有功功率的相对误差和TICTab.3 Relative error and TIC of branch active power
深入分析表2~表4中的数据可以发现,越接近分布式电源的接入点,RITCM得到的输出变量的统计特征与MCS的结果差距越大,这也可以成为该方法今后改进、优化的一个方向。

表4 支路无功功率的相对误差和TICTab.4 Relative error and TIC of branch reactive power
重复上述仿真,得到考虑风电/风电出力相关性的PLF计算结果,如表5所示,表中只给出了几个指标的平均值。
由表5数据可知:RITCM输出变量的期望具有很高的准确性,也具有较高的预测精度,但输出变量标准差的准确性有待提高,与考虑风电/光伏出力相关性的分析相一致。

表5 考虑风电/风电出力相关性的PLF仿真结果Tab.5 Simulation results of PLF considering the correlation between wind turbine outputs
以考虑风电/光伏出力相关性的PLF仿真比较2种方法计算时间,MCS用时75.605 s,采用RITCM方法用时2.631 s,计算时间大大减小。
4 结论
本文考虑了接入同一配电网的风电/风电、风电/光伏出力的相关性,提出一种基于Rosenblatt逆变换和半不变量法的概率潮流计算方法RITCM,仿真对比分析结果表明以下结论。
(1)RITCM的适用范围广泛,能够适用于具有正相关性的分布式电源出力,也适用于具有负相关性的分布式电源出力,且都具有较高的准确性。
(2)采用RITCM方法计算考虑分布式电源出力相关性的配电网概率潮流,能够准确反映节点电压幅值、支路潮流的概率特征,具有较高的准确性和预测精度,但该方法在计算输出变量标准差时的准确性有待提高。
(3)RITCM避免了大量重复性的确定性潮流计算,相比于传统的MCS方法,RITCM的计算步骤少,计算速度大幅提高。
