考虑需求响应的电力系统灵活性资源优化配置
2021-06-10鉴庆之刘晓明杨金叶刘春阳王宪刘冬
鉴庆之,刘晓明,杨金叶,刘春阳,王宪,刘冬
(1.国网山东省电力公司经济技术研究院,山东省济南市 250021;2.山东大学电气工程学院,山东省济南市 250061)
0 引言
受随机气象因素的影响,光伏、风电等可再生能源的出力具有随机性与波动性特征[1-3]。因此,可再生能源的大规模并网正严重加剧电力系统运行面临的不确定性程度,从而给电力系统的稳定运行和功率平衡带来巨大挑战[4]。这要求在电力系统的资源配置过程中,不仅要保证长期电力电量平衡,还需对短期甚至超短期的电力电量平衡提供保障[5],满足负荷需求变化与风光等间歇性电源出力突变时的短时功率平衡需求,即电力系统的灵活性需求[6-7]。
有学者指出[8],在下一步电力系统规划中,应强调系统优化,降低常规火电机组的冗余规划容量,提高灵活调峰电厂在电源结构中的占比,并通过电价机制激励需求侧响应来改善负荷特性,全面提升电力系统的灵活性来适应高比例可再生能源的运行。文献[9]提出了应对未来高度不确定性的灵活电源规划模型,能兼顾经济性和灵活性,在规划成本最小的前提下拥有最大的灵活性。在高比例新能源并网规划中,需要量化系统的灵活性[10],灵活性评估对数据更加依赖,且需要更加详细的系统仿真模型。文献[11]基于灵活性指标将常规电源分为低、中、高3类灵活性机组,并基于电源规划模型,研究既定风电消纳目标下的最优电源规划结果。
电力系统灵活性充足与否在运行阶段才能得到检验,对于电力系统中的既有资源,使配置结果既保证系统的运行灵活性又能兼顾系统运行的经济性,是灵活性优化配置的首要问题。文献[12]提出一种支持欧洲电力系统灵活性的综合调度方法,将系统爬坡和实时调度相结合,增强了系统可靠性和灵活性;文献[13]提出电力系统超短期优化调度模型,并给出面向灵活资源配置的超短期优化调度方法;文献[14]对各类灵活性资源进行整合,将输电网传输容量考虑在内,构建了基于Bender分解方法的灵活性资源优化配置模型。
需求响应可以通过价格信号或激励机制改变电力用户固有的消费模式,在资源配置过程中考虑需求响应,可进一步提高系统运行的经济性和灵活性。文献[15]提出了一种在实时电力市场中考虑爬坡能力的调度方法,提高了电力系统应对不确定性的能力;文献[16]综合考虑系统灵活性约束和需求响应在系统调度中的贡献,提出源网荷协调规划模型,可提高系统灵活性和对可再生能源的消纳能力;文献[17]提出了一种储能和需求侧响应配合的规划模型,使规划结果可获得更高的经济效益。
综上所述,针对高比例可再生能源与灵活性资源的多层次协调规划方法尚不完善。因此本文提出一种考虑需求响应的电力系统灵活性资源优化配置方法,并结合多层次迭代和松弛技术,综合考虑规划层、运行层和灵活层3个层次,最终实现兼顾系统经济性和灵活性的资源优化配置。
1 间歇性电源与灵活性电源建模
1.1 间歇性电源
1.1.1 Copula函数理论基础
假设随机向量 [x1,x2,···xn]的联合分布函数为H(·), 其边缘分布分别为 F1,F2,···,Fn,则存在一个Copula函数 C (·)满足:
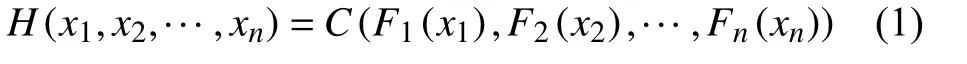
若F1,F2,···,Fn是 连 续 的,则 C(·)唯 一 确 定,则由式(1)确定的 H(x1,x2,···,xn)是具有边缘分布F1,F2,···,Fn的n元联合分布函数。
对式(1)两边同时求偏导,可以得到随机向量[x1,x2,···xn]的 联合概率密度函数 h (·):

式中:c(∙)为Copula概率密度函数; fi(xi)为 xi的概率密度函数。
1.1.2 考虑时空相关性的风光出力模拟
考虑风电出力和光伏出力的时空相关性,基于正态Copula函数理论,建立两者联合概率分布模型,具体步骤如下:
1)设模拟时段为T,各时段光伏电站出力为xs,t、 风电场出力为 xw,t;
2)基于历史数据求各时段光伏出力概率密度 fs,t(xs,t) 和 概率分布 Fs,t(xs,t), 其中 t =1,2,···,T;
3)同理可得各时段风电出力概率密度fw,t(xw,t)和概率分布 Fw,t(xw,t), 其中 t =1,2,···,T;
4)构建 2T 维Copula函数,其中 ” T”代表时间维度、 ” 2”代表空间维度,空间相关性指同一时段内风电和光伏出力的相关性,故空间维度为 ”2”;
5)基于风电、光伏历史出力数据求解Copula函数相关系数,并生成一组具有相关性的随机值{us,t,uw,t|t=1,2,···,T};
1.2 储能电站
储能电站可以作为灵活资源平抑风电光伏等可再生能源出力的波动[18]。在并网运行过程中,只需考虑储能电站的运行特性,这些特性可以表示为一系列的不等式约束条件:
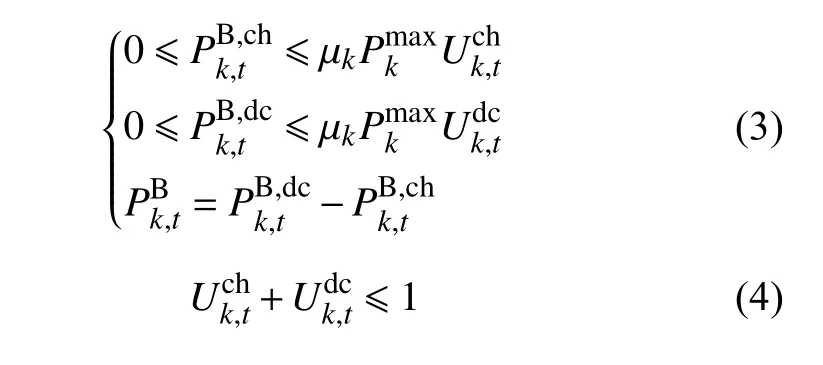

式(3)—(6)分别为储能的充放电功率上下限约束、工作状态约束、充放电的电量存储约束、储能装置调度周期始末容量相等。t、k分别为时段数和储能装置数。其中:为储能充电、放电工作状态;为储能充电、放电功率;为 储能装置对电网注入功率; µk为裕度系数;为储能装置k的额定功率; Ek,t为储能装置k在t时刻的实际存储电量;为储能装置k的最大和最小存储电量; δk为储能装置k的能量自损耗系数;为储能装置充电和放电过程中的能量转化效率;T为调度周期内总时段数。
1.3 灵活机组
除储能电站之外,部分火电机组和水电机组也可以作为灵活性资源参与电力平衡。其灵活性主要体现为相比常规机组具有更宽的调节裕度和更高的爬坡速率。具体模型在3.3.3节灵活机组增调模型中介绍。
2 需求响应参与调度模型
2.1 峰谷平分时电价模型
当采用峰谷平分时电价时,由于相邻时间段的电价之间存在着替代关系,因此不仅需要考虑某一时段电价水平,还需要考虑相邻时间段的电价水平[19]。为了描述这种峰谷电价需求弹性,我们用自弹性系数 εii和 交叉弹性系数 εij表 示:

式中:i、j为i时段和j时段;Pi为实施峰谷电价前i时段的用电量;ΔPi为实施峰谷电价后i时段用电量的变化;Qi表示实施峰谷电价前i时段电价;ΔQi表示i时段的电价变化量。
基于自弹性系数和交叉弹性系数可以建立一个分时电量与电价的弹性矩阵:
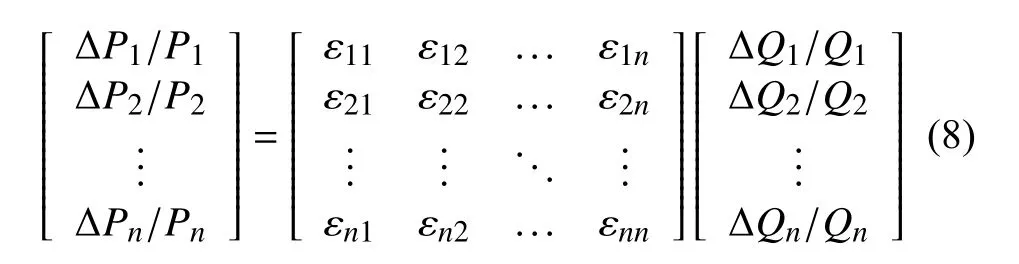
在供需平衡的条件下,负荷响应的模型可以表示为:
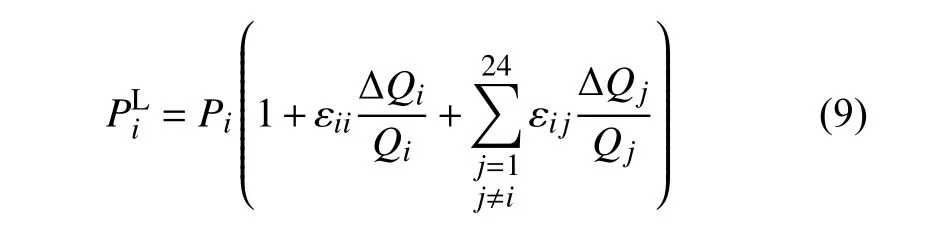
实施峰谷平分时电价后售电收入差额为:

约束条件如下。
1)用电总量不变约束:

式中:Pf、Pp、Pg、分别为实施峰谷分时电价前和实施后的各时段总用电量。
2)电价上下限约束:

式中:Qh、Ql为电价上下限。
2.2 可中断负荷模型
可中断负荷是一种基于激励的需求响应类型,其实现方式为供电公司与部分用户预先签订可中断合同,在系统不能满足调峰需求时可以选择中断部分或全部可中断负荷,并给予该部分用户一定的经济补偿,从而达到维持系统有功功率供需平衡的目的[20]。可中断负荷参与调度的成本函数为:

式中: ρIL为 可中断负荷补偿价格;为t时段参与调度的可中断负荷总量。
约束条件主要有:
1)可中断负荷中断量约束:
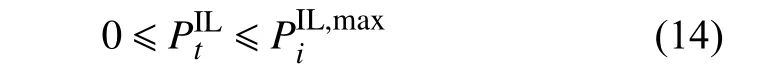
2)可中断负荷最大中断可持续时间约束:

3)可中断负荷最小调用时间间隔约束:

式中: Tno为可中断负荷连续未被调用时间;为可中断负荷的最小调用时间间隔。
4)可中断负荷调度周期内总调用时间约束:

式中: Tsum,max为调度周期内可中断负荷允许被调用的总时间。
3 电力系统灵活性资源配置模型
电力系统灵活性资源优化配置模型由需求响应模型和优化配置模型两部分组成,两者之间数据传递如图1所示。从图1中可以看出需求响应模型有2种:包括峰谷平分时电价模型和可中断负荷参与调度模型,其输出数据作为优化配置模型的输入数据。而在优化配置模型中考虑到不同时间尺度,又分为规划层、运行层和灵活层3个层次。规划层输出机组投产情况作为运行层输入数据,而运行层将现有备用情况反馈给规划层,若不满足备用需求,则需重新规划。运行层输出机组组合结果作为灵活层输入数据,灵活层则根据是否满足灵活性需求判断是否返回运行层重新求解机组组合。
3.1 含灵活资源在内的电源规划模型
3.1.1 目标函数
电源规划过程中我们主要考虑经济因素,包括常规电厂、可再生能源电厂、水电厂和储能电站的投建成本,所以目标函数为规划年内总成本:

式中:T1为规划期内总月数; GN1、 RN1、 HN1、BN1分别为规划期内待投建常规、可再生能源、水电、储能电站数;为第t个月常规电厂新增容量和单位建设成本;为第t个月可再生能源电厂新增容量和单位建设成本;为第t个月水电厂新增容量和单位建设成本;表示第t个月新增常规、可再生能源、水电、储能是否需要分摊的初始投资成本和使用年限;、为第t个月新增储能功率容量和能量容量;为对应的单位功率容量和单位能量容量建设成本;ζt为第t个月的折现值系数;σ为年贴现率。

图1 考虑需求响应的电力系统灵活性资源优化配置Fig.1 Optimal allocation of power system flexible resources considering demand response
后续模型中会用到已有各类电源的总装机容量,因此令:

3.1.2 约束条件
1)电力约束:

2)常规电厂最大、最小利用小时约束:
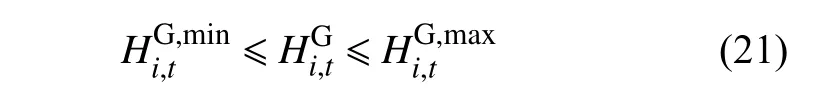
3)可再生能源装机占比约束:

式中: αt为第t个月可再生能源装机占比。
4)水电厂电量约束:

5)考虑到电源投资决策模块和短期运行模拟模块的交互,还应考虑负备用约束:

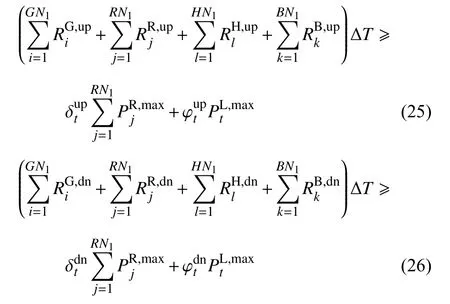
3.2 短期运行模拟模型
3.2.1 目标函数
短期运行模拟模型中的目标函数即为最小化成本,包括发电带来的煤耗成本和机组开停机成本、储能装置的维护成本和折旧费用、弃风弃光成本、实施分时电价后收入差额、可中断负荷补偿成本:
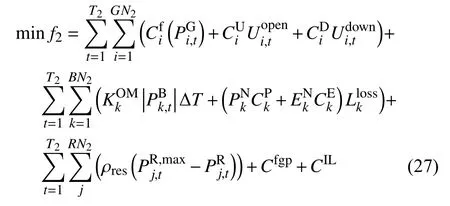
式中: GN2、 BN2、 RN2为参与短期调度的常规、储能、可再生能源机组数;T2为短期调度周期内时段数;分别为机组i的煤耗成本、启动成本和关停成本;为常规机组i在t时刻的实际出力;为机组i在t时段的启动状态变量和停机状态变量;为第k个储能装置的单位电量运行维护成本;储能装置k在t时刻的实际出力;为第k个储能装置的额定容量和额定功率功率;为储能装置k的单位容量和单位功率安装成本的现值;为储能装置k的寿命损耗系数[21];为可再生能源电厂l的可用资源量和实际出力; ρres为弃风弃光惩罚因子。
上式中机组i的煤耗成本可表示成二次函数的形式:
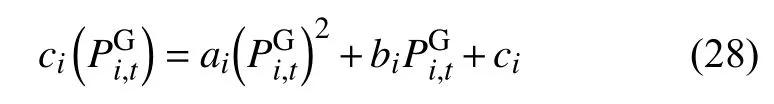
式中:ai、bi、ci为机组i的煤耗系数。
3.2.2 约束条件
1)系统有功功率平衡约束:
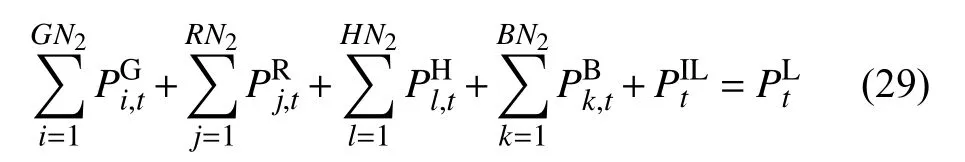
2)不等式约束:


式(30)—(35)分别为机组出力上下限约束、爬坡约束、系统热备用约束、起停费用约束、起停时间约束、可再生能源出力约束。其中: Ui,t为常规机组i在t时刻的启停状态;为机组的上、下爬坡速率;ρ为热备用系数;为机组i的最大启动、关停成本限制; Hi、 Ji为组i的单次启动、关停成本;TS、TO为最小关停、开机时间;为可再生能源的可用资源量。
此外,水电厂电量约束同式(23),储能约束同式(3)—式(6)。
3.3 超短期运行模拟模型
3.3.1 目标函数
超短期运行模拟过程中认为常规机组的起停状态不发生变化,因此机组开停机成本可以不考虑、同时储能装置的折旧费用和维护成本也可以忽略。但考虑到可能会出现上下爬坡容量不足和调峰容量不足的情况,所以需增加相应的处罚项。超短期运行模拟的目标函数为:

式中:T3为运行时刻数;G N3、 R N3分别为参与超短期调度的常规机组数和可再生能源机组数;为上、下调峰功率松弛;为上、下爬坡功率松弛; ρ1~ρ4为相应惩罚因子。
3.3.2 约束条件
约束条件主要有:

式(37)—(40)分别为系统功率平衡约束、常规机组运行爬坡约束、新能源机组运行约束、可中断负荷中断量上下限约束。其中,为t时刻下调峰功率松弛; HN3、 BN3为参与短期调度的水电机组数和储能装置数。
考虑到可能出现灵活资源的爬坡容量不足的情况,因此需对爬坡约束进行松弛:
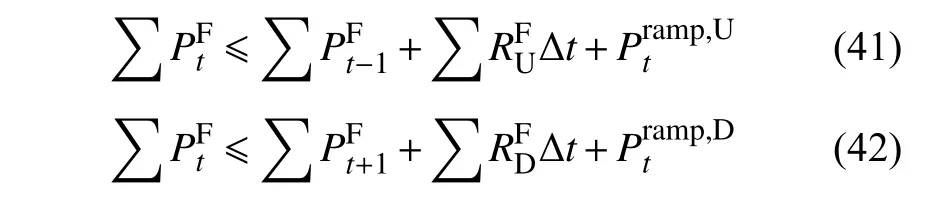
3.3.3 灵活机组增调模型
当系统灵活性不足时需要增加灵活机组开机,同时为了不对系统的下调峰能力造成影响,需要减少常规机组的开机。灵活机组增调模型中的目标函数主要包括灵活机组增加开机的成本和常规机组关机的成本:
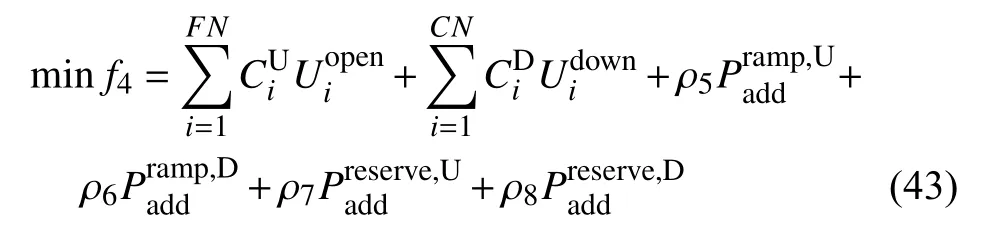
约束条件主要有上下调峰和上下爬坡缺额限制约束:
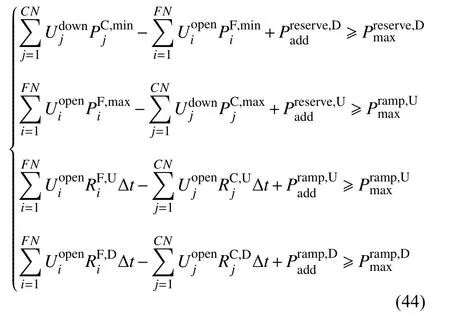
3.4 模型求解方法
3.4.1 煤耗成本线性化
上述模型中的煤耗成本为二次函数形式,需进行分段线性化处理:
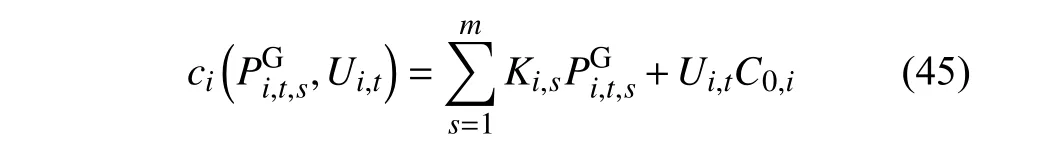
m为总分段数; Ki,s为分段线性化后煤耗函数各段的斜率; C0,i为机组以最小出力运行时的煤耗成本;为机组各分段的出力。
3.4.2 求解流程
规划层、运行层和灵活层3个层次需迭代求解,同时为了提高计算的鲁棒性,在运行层和灵活层求解过程中引入了上下爬坡不足和上下调峰不足等松弛变量,因此整个求解过程需结合迭代技术和松弛技术。将煤耗成本线性化后,上述电源优化投资决策模型和超短期运行模拟模型可转化为混合整数线性规划模型,但短期运行模拟模型中计及实施分时电价后的售电差额,仍为混合整数二次规划模型。因此,该优化配置模型采用CPLEX软件求解,流程如图2所示。

图2 多层次迭代求解流程图Fig.2 Flowchart of multi-level iterative solution
4 算例分析
4.1 算例介绍
以某区域实际情况为算例,规划期选择7年,验证上述模型的有效性。具体数据如表1所示,其中常规机组包括煤电机组和气电机组。

表1 规划期机组信息Table 1 Unit information in planning period
4.2 结果分析
将该算例代入所提模型中进行求解,以月为时间尺度进行规划,可得规划期内电力平衡和负荷月变化趋势如图3所示。
根据电源规划结果选取典型日进行短期运行模拟,该算例中选取规划期第58个月内某典型日进行调度求解,该典型日内已有机组(包括规划新增的机组)信息如表2所示。
根据以上机组信息分别进行未考虑需求响应和考虑需求响应短期运行模拟,初次迭代结果中,该典型日内各类机组出力如图4、图5所示。
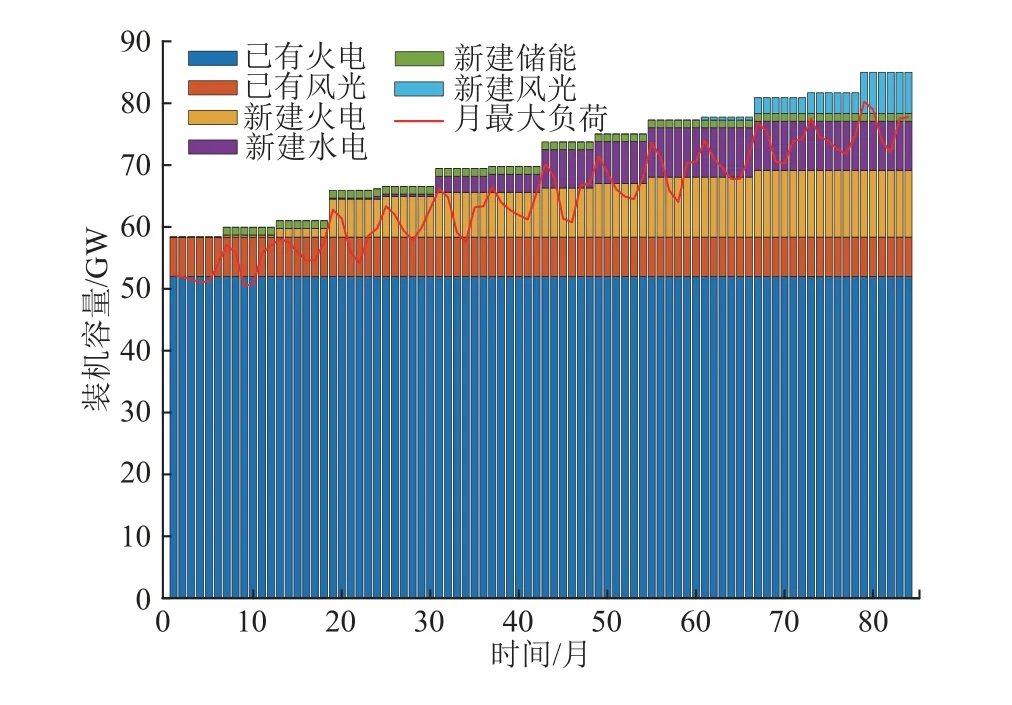
图3 规划期电力平衡Fig.3 Power balance in planning period

表2 短期调度机组信息Table 2 Unit information of short-term scheduling
其中,峰谷平时段划分结果如表3所示。

图4 未考虑需求响应短期运行模拟结果Fig.4 Short-term operation results with demand response not considered
对比分析图4和图5可以看出,考虑需求响应后,日内峰谷差减小、负荷曲线更加平滑,同时储能充放电频率和充放电容量减少,有利于储能装置的维护和电网的经济运行。
选取7:00—9:00光伏出力明显上升时段进行电力系统超短期运行模拟,调度时间间隔选为5 min。可得初次迭代结果如图6、图7所示。

图5 考虑需求响应短期运行模拟结果Fig.5 Short-term operation results with demand response considered

表3 峰谷平时段划分Table 3 Division of peak-valley-flat time period
对比分析图6和图7可以看出:未考虑需求响应时电力系统存在明显的弃风弃光现象,造成大量风电和光伏的浪费,不利于大规模可再生能源的并网;计及需求响应后,系统弃风弃光量大幅度降低,接近于零,可以得出考虑需求响应可以提高系统的灵活性,进而提高对可再生能源的消纳能力。
考虑需求响应和未考需求响应的规划和运行成本如表4所示。

图6 未考虑需求响应超短期运行模拟结果Fig.6 Ultra-short-term operation results with demand response not considered

图7 考虑需求响应超短期运行模拟结果Fig.7 Ultra-short-term operation results with demand response considered

表4 成本数据Table 4 Cost data
表中规划运行成本为迭代后最终结果,而弃风弃光和调峰缺额为初次迭代结果。对比分析未考虑需求响应和计及需求响应后的各阶段所需成本,可以看出考虑需求响应后各阶段所需费用均低于未考虑需求响应时所需费用。
当不考虑需求响应时,由于日内峰谷差偏大,初次迭代求解结果不能满足系统灵活性需求,存在明显的弃风弃光现象。为了满足灵活性需求,需调用更多的灵活机组。当系统已投建机组不能满足备用需求时,需重新进行电源规划,优先投建爬坡能力强的灵活性机组,故会增加一定的投建成本。
当考虑需求响应时,需求响应可作为电力系统需求侧的灵活性资源参与调度,虽然初次迭代求解结果仍不满足系统灵活性需求,有少量的弃风弃光量,但只需在短期运行模拟中增调灵活机组,用爬坡能力较强的机组替代爬坡能力较弱的机组即可,系统已投建机组可以满足备用需求。
5 结论
本文针对考虑需求响应的电力系统灵活性资源优化配置问题进行研究。首先建立考虑时空相关性的风光不确定出力模型,其次对储能等灵活性资源进行建模,再次建立峰谷平分时电价和可中断负荷两种需求响应模型,最后兼顾系统经济性和灵活性,建立综合考虑运行层、规划层和灵活层的电力系统灵活性资源优化配置模型。
以某区域实际情况为例,对比分析未考虑需求响应和考虑需求响应之后的计算结果,可以得出增调灵活机组和需求响应参与调度均能提高系统灵活性,同时提高系统对可再生能源的消纳能力,最终验证了所提灵活性资源配置方法的经济性和有效性。
