基于混沌特征改进鲸鱼优化算法-相关向量机的超短期光伏发电输出功率预测

倪安安，王育飞，薛花

（上海电力大学电气工程学院，上海市杨浦区 200090）

0 引言

近年来，光伏发电在能源供应体系中的作用愈加凸显[1]。然而，由于光伏发电输出功率影响因素多、耦合复杂、随机性强且变化频率快，导致光伏发电输出功率预测难度大，准确率难以满足电网实际需求，部分地区弃光现象严重，给电力系统的调峰调频和并网消纳带来一定挑战。利用储能系统对光伏发电输出功率波动进行实时平抑，可增加光伏发电的利用率，保证电网安全稳定运行；提高光伏发电输出功率预测准确度能有效帮助储能系统制定平滑控制策略[2]。

目前，针对光伏发电输出功率预测的研究方法总体可分为物理法、统计法和元启发式学习法[3]。其中物理法基于气象因素和光伏组件参数间光电能量转换的物理联系进行预测，建模过程复杂且要求气象数据质量较高[4]；统计法基于光伏电站历史数据的统计学规律，应用概率统计、聚类和谱分析等方法展开预测，建模过程简单，所需信息易于获取，在实际工程中应用前景广阔[5-7]；元启发式学习方法通过挖掘光伏发电输出功率、气象等历史数据的变化规律，基于人工智能算法寻找历史数据与未来光伏发电输出功率之间的映射关系[8]。目前利用数学方法模拟神经元活动的误差反向传输(back propagation, BP)和长短期记忆(long short-term memory, LSTM)神 经 网 络 方 法，以及利用核函数进行回归预测的支持向量机(support vector machine, SVM)、最小二乘支持向量机(least squares support vector machine, LSSVM)方 法，已在光伏预测领域得到广泛应用[9-11]。其中SVM利用支持向量样本集决定预测结果，具有一定的鲁棒性，但计算复杂、耗时长。LSSVM利用误差变量的正则项确定最终的决策函数，一定程度上降低了SVM支持向量样本集的求解难度，提高了收敛速度。为进一步提高这类预测方法的稳定性和适用性，通常采用寻优算法优化参数以获得组合预测方法，提高算法预测准确度[12]。然而，这些方法并未从根本上解决SVM惩罚系数难以确定、核函数受Mercer条件限制的问题。文献[13]提出一种基于贝叶斯框架的稀疏有监督学习方法相关向量机(relevance vector machine, RVM)，RVM可以在先验参数结构下结合自相关判定，移除统计学上不相关的数据点获得稀疏化的概率方法，相较SVM极大地减少了核函数的运算量，具有良好的稀疏性、泛化能力，已在趋势预测领域得到一定的应用[14]。考虑到RVM的泛化能力受核函数影响，采用寻优算法迭代RVM的解析解获得最优核函数参数，能进一步提高预测方法准确度和适应性。鲸鱼优化算法(whale optimization algorithm, WOA)是通过模拟座头鲸捕杀猎物行为设计的一种启发式算法，具有结构简单、调节参数少且全局寻优能力强等优点[15]，因此，基于WOA优化RVM对光伏发电输出功率进行预测是一种提高预测准确度的可能途径。文献[16]通过分析光伏序列的混沌特性，利用混沌相空间重构方法挖掘光伏时间序列的动力学本质，结合径向基神经网络预测光伏发电输出功率，表明混沌理论可用于提高光伏发电输出功率预测准确度。在此基础上，文献[17]将光伏电站气象因素和混沌特征结合，优化方法输入量品质，同时采用双模式布谷鸟算法改进小波神经网络，进一步提高预测准确度。

为提高方法适应性、改善预测准确度，本文通过提取光伏时间序列混沌特征，挖掘其隐藏的动力学信息与预测方法间的物理联系，提出一种基于光伏发电输出功率混沌特征改进的WOA-RVM预测方法。建模过程简单，具有一定的实际应用潜力。

1 基于混沌特征确定RVM核函数

1.1 光伏发电输出功率混沌特征提取

为从光伏发电输出功率时间序列中得到有用的混沌特征进行分析，需对原始序列进行相空间重构，将光伏发电输出功率原始的动力学行为以混沌吸引子形态在相空间内无奇异地呈现出来。相空间重构的关键在于选取合适的混沌参数：时间延迟 τ和嵌入维数m[18]。

1.1.1 基于伪近邻法计算嵌入维数

混沌对初值具有敏感依赖性，初值的微小差异会导致吸引子轨道演化的巨大差别，影响预测准确度。由于光伏序列在采集过程中难免混入噪声，为在m维空间内恢复体现光伏系统规律性的混沌吸引子，采用抗噪性能较好的伪近邻法计算m。取光伏序列 X 中任意相点 Xi，则在高维相空间内存在其最邻近相点 XiNN，相点间欧式距离为 Ri，其中

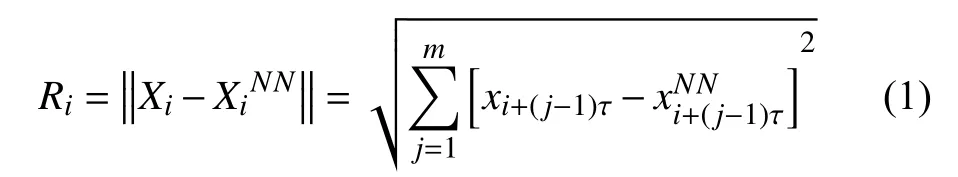
当相空间的维数增加到m+1维时，两点间的距离变为 Ri+1，两邻近点之间的距离变化为：

若 Ri+1大 于 Ri，则认为混沌吸引子中两个不相邻的点投影到低维轨道上变成相邻的两点，称这两个点为伪近邻点，即这样的近邻点是虚设的。真正的近邻点距离为 Rm， 定义两邻近点距离与 Rm的比率为：

式中：ai为伪近邻率，当两邻近点距离不随维度m增大而变化时，即 Ri+1与 Ri相等。通过迭代 Xi和XiNN的值， ai和设定判据的伪近邻率同时到达零点，此时对应的m即为最小嵌入维数。

1.1.2 基于复自相关法计算时间延迟

时间延迟 τ为延迟坐标，决定吸引子的耗散程度，即光伏序列各时刻点的相关性。由于光伏系统是复杂的非线性系统，故采用复自相关法计算τ[19]。光伏序列 X 的复自相关函数Cτ定义如下：

式中：xk为k时刻的光伏发电输出功率，N=n−(m−1)τ为 相点总数，x¯为样本均值。理论上所有大于或等于 τ处，复自相关函数为0。

相空间重构后得到的相轨迹矩阵如下式所示：

1.2 基于混沌特征确定RVM高斯核径向范围

RVM可以有效解决小样本、高维、非线性系统的回归问题，故在建立高维空间内光伏序列的动力学方法基础上，采用RVM构造预测方法。

式中： ω0为 方法的偏差； ω=(ω0,ω1,···,ωn)为权值，假设其服从 (0,α−1)高 斯分布，每一个权值ωi定义高斯分布的先验概率分布来约束最大似然估计超参数α，通过跟踪过去的评估结果，选择合适的 α来评估泛化能力，实现方法的回归拟合；εi为独立分布的高斯白噪声； k(x,xi)为径向基(RBF)核函数，又称为高斯核函数，其表达式如下：

式中：δ为高斯核核宽，用训练向量参数化的核函数来定义基函数 ϕ(xi)≡k(x,xi)，RVM基函数矩阵 为 Φ=[Φ(x1),Φ(x2),···,Φ(xN)]T。 其 中，Φ(xi)=[1,k(xi,x1),k(xi,x2),···k(xi,xN)]T。

根据相轨迹矩阵，构建预测方法的输入和输出变量如表1所示，即将相空间中的第k个相点作为输入变量，将第k+1个相点的最后一维作为输出变量。

根据输入和输出之间的映射关系，基函数矩阵变为：

式中： p=k+(m−1)τ。

核宽 δ愈大，径向范围愈大，若超出这一范围，高斯核函数快速衰减至0，RVM核函数失去泛化能力，因此需要根据光伏序列的相轨迹矩阵调整核宽参数。随着维度的增加，通过高斯核函数暴力枚举迭代得到RVM核参数，将增加时间复杂度。各向异性高斯核通过提取同一纬度样本的欧式距离来设定核参数，其效果优于传统高斯核的特征选择[20]。欧氏距离

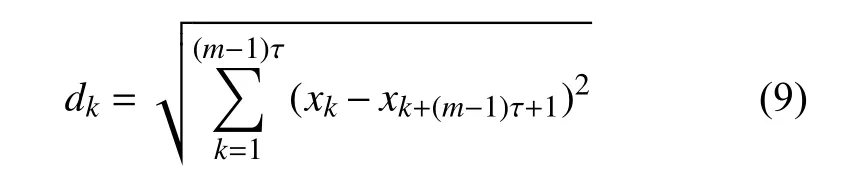
可见，随着维度的增加，光伏相空间矩阵的欧式距离d增大，为使高斯核函数工作在限定范围内，通过将各个相点的欧式距离作为核宽赋值给对应的基函数矩阵，采用各向异性高斯核自适应确定高斯核核宽，即核函数径向范围，核函数表达式如下：

表1 预测方法的输入变量与输出变量Table 1 Input and output variables of forecasting method

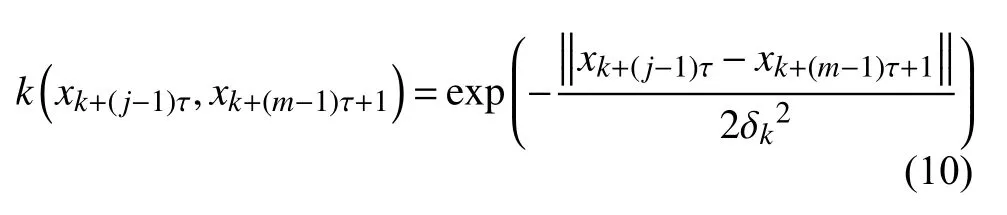
式中： j∈[0,m−1]， δk=dk。

2 WOA- RVM超短期预测方法

2.1 基于WOA优化RVM预测方法

为提高RVM方法在各典型天气下的适应性，采用WOA优化RVM核函数的核宽和最大似然估计超参数α，WOA寻优步骤为：

1)包围猎物。

WOA算法通过搜索代理包围目标来寻找最佳位置，这一行为可由如下方程表示：

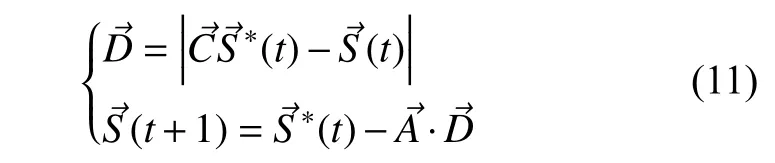
2)泡泡网捕食。

通过式(13)螺旋更新位置：

式中，b是定义对数螺旋形状的常量系数；l是属于 [−1,1]区 间的随机数；是第i次迭代时与猎物的距离。

3)搜索猎物。

接着，建立基于WOA优化的RVM预测方法，其流程如图1所示。

具体实现步骤如下：

1) 确定WOA中搜索代理数量 magent为3，单个搜索代理最大寻优次数为1000，最大迭代次数Tmax为 20，寻优参数上限 ub为 20、 下限 lb为 210；

图1 基于WOA优化的RVM预测方法Fig.1 WOA-optimization based RVM forecasting method

2)初始化鲸群位置，并根据RVM预测方法，计算初始的预测值，以最小均方差作为适应度函数，然后根据式(15)计算出每个个体的适应度值。

6)以真实值和预测值的最小均方差作为适应度值，重复步骤3)、4)、5)，达到最大迭代次数时，输出全局最优解作为RVM方法的核函数参数，得到最终的WOA-RVM预测方法。

2.2 基于混沌特征改进的WOA-RVM预测方法

为进一步提高RVM的回归拟合能力，基于光伏发电输出功率混沌特征的提取，利用WOA算法对RVM核函数参数进行寻优，建立一种改进的WOA-RVM光伏发电输出功率组合预测方法。具体流程如图2所示。首先，基于光伏发电输出功率时间混沌特征提取重构相空间，恢复原始序列混沌吸引子动力学演化轨迹；接着，基于相轨迹矩阵自适应确定RVM高斯核径向范围；然后，选取合适的训练集和预测集，利用组合预测方法进行光伏发电输出功率超短期预测。

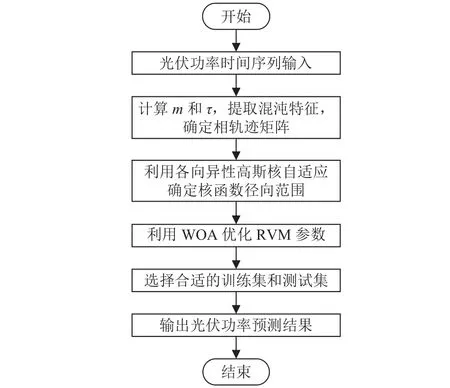
图2 基于混沌特征改进的WOA-RVM预测方法Fig.2 The forecasting method based on chaotic characteristic-improved whale optimization algorithm and relevance vector machine

3 算例结果分析

为验证所提方法在光伏发电输出功率超短期预测上的有效性和优越性，选择美国国家标准与技术研究所(NIST)提供的光伏阵列61 天出力数据进行仿真[21]。采样时段为6:00—19:00，采样步长5 min，一天共157个采样点，光伏阵列额定功率243 kW，在Matlab 2016a环境下分析5种典型天气下的光伏发电输出功率超短期预测效果。

3.1 混沌参数计算

分别采用伪近邻法和复自相关函数法确定混沌相空间重构参数，统计量结果见图3。

由图3(a)知，在m为6处，3个判据同时为0，因此m为6。图3(b)中，时间延迟为21处初次出现复自相关函数为0，因此时间延迟 τ为21。

3.2 混沌特征对预测准确度影响分析

为验证混沌特征提取对WOA-RVM方法的提高效果，选取光伏发电输出功率的前56天作为训练集，分别从后几天(以晴天为代表的非突变天气和以多云转晴、晴转多云、多云、阴雨天为代表的突变天气)中各挑选1天作为测试集，分别从收敛速度和预测绝对误差两方面进行比较。

图4为两种预测方法适应度进化曲线对比，随着迭代次数的增加，所提预测方法迅速收敛，而WOA-RVM预测方法前期收敛速度较慢，且收敛时预测准确度低于所提方法。

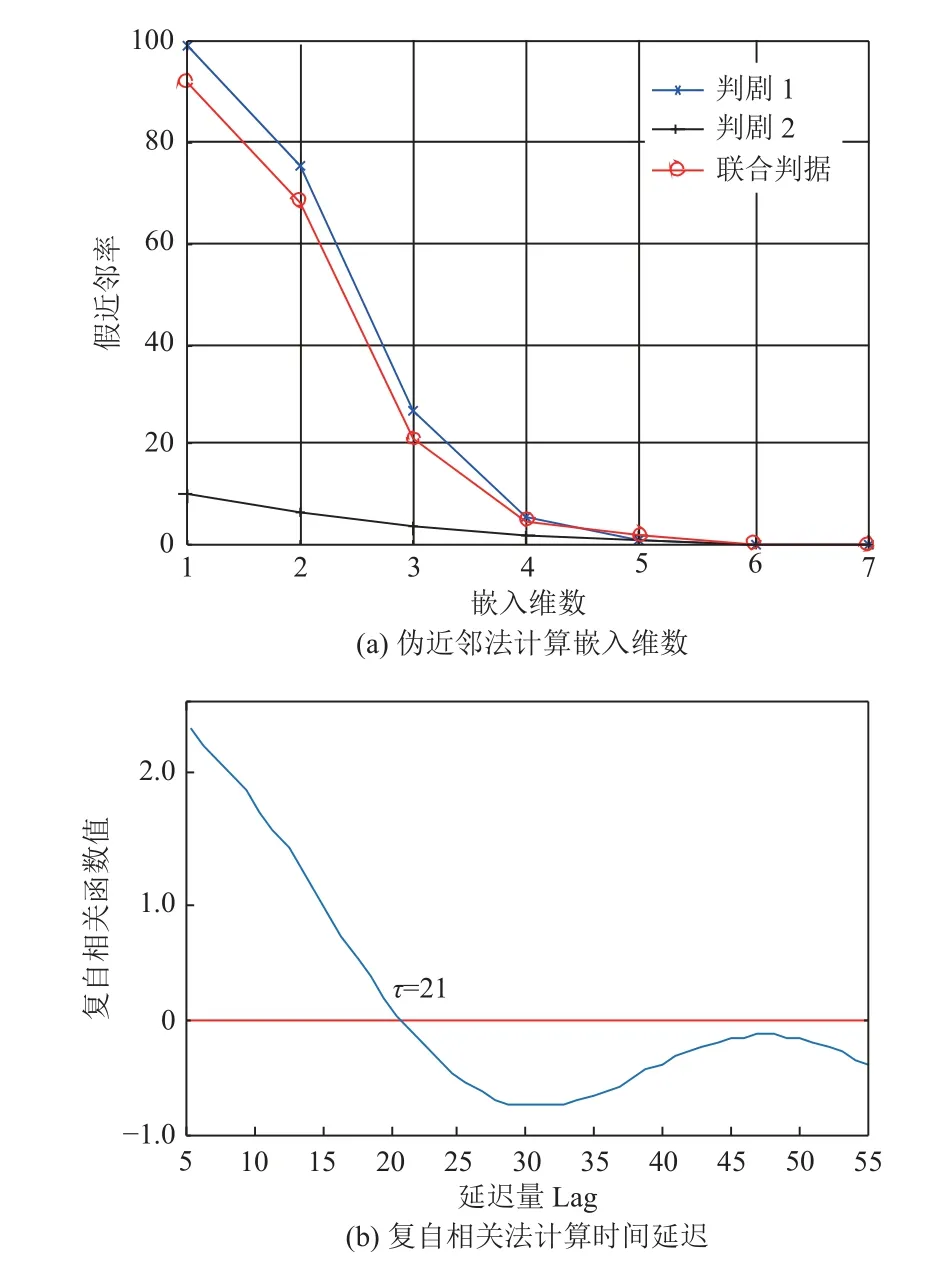
图3 混沌参数计算Fig.3 Calculation of chaotic parameters

图4 不同预测方法的适应度值进化曲线对比Fig.4 Fitness values comparison of the proposed method and that of WOA-RVM method

图5 为所提方法与WOA-RVM的绝对误差曲线对比，所提方法预测的准确度和适应性明显高于WOA-RVM方法。

3.3 应用分析

为客观对比分析所提方法的预测性能，利用WOA优化LSSVM和SVM核宽参数得到WOALSSVM和WOA-SVM组合预测方法，并将所提方法、WOA-LSSVM、WOA-SVM、RVM、BP和LSTM方法基于单步循环滚动局域预测机制， 进行光伏发电输出功率超短期预测，同时考虑到BP和LSTM鲁棒性较差，分别独立运行30次取均值得到最终预测值，各方法预测结果见图6。

图5 绝对误差曲线对比Fig.5 Comparison of absolute error curves

图6 各种天气情况下不同预测方法的预测结果Fig.6 Forecasting results by different forecasting methods under various weather situation

由图6可见，在5种典型天气下，各预测方法都与实际值有不同程度的偏差，其中BP和LSTM方法整体偏差较大。各预测方法在晴天时跟踪性能较好，阴雨天气误差波动最为剧烈。在图6(a)晴转多云天气和图6(d)多云转晴天气10:00—11:00这部分光伏发电输出功率急剧上升或下降的时段，从局部放大图上可以看出，BP和LSTM方法预测结果均出现了较显著的偏差，无法很好反映出光伏发电输出功率变化趋势，而利用核函数进行拟合的WOA-LSSVM、WOASVM和RVM方法误差波动较小，跟踪性能较好。在图6多云天气9:00—10:00和图6(c)(e)阴雨天气11:00—12:00，这部分波动较频繁的时段，BP和LSTM方法跟踪性能明显较差，预测准确度有待进一步提升，WOA-LSSVM、WOA-SVM和RVM方法虽有一定的时滞现象，但能较好反映光伏发电输出功率波动情况，误差波动范围有所减小。所提预测方法通过重构混沌相空间提取原始光伏发电输出功率时间序列的隐藏信息，建立混沌特征与RVM高斯核函数的物理联系，对光伏发电输出功率突变和波动更加敏感，尤其在光伏发电输出功率低而剧烈波动的拐点处，跟踪性能最好。

为定量分析预测结果，利用标准化平均相对误差百分比( NMAPE)、标准化均方根误差百分比( NRMSE) 、标准化平均绝对误差百分比( NMAE)和决定系数百分比(R-square)对预测结果进行评价，对比结果见表2。各项指标表达式分别为：

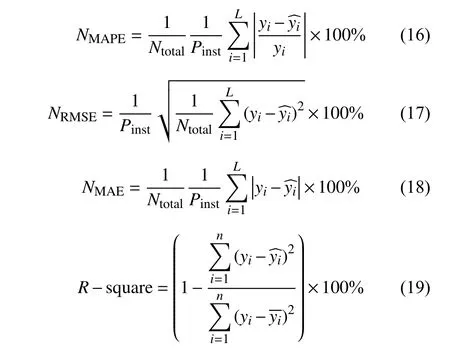
式中： Ntotal为 预测点个数； Pinst为额定装机容量；yi为 实际出力；为预测值；为实测值的均值。

表2 不同天气情况下预测误差分析Table 2 Analysis of forecasting errors under various weather situations

从表2可以看出，5种典型天气情况下，所提预测方法通过挖掘光伏发电输出功率的混沌特征并将WOA和RVM两种方法结合起来，预测准确度得到进一步提升。从表2可以看出，除了个别指标略差于LSTM预测方法，所提出的方法在不同天气条件下的表现一般优于所有对比方法，表中以粗体显示。并且在以晴天为代表的非突变天气情况下，各预测方法的预测性能差异最小，且预测效果要优于突变天气情况。所提方法总体NMAPE比WOA-LSSVM、WOA-SVM、RVM、BP和LSTM预测方法分别降低13.80%、26.26%、38.49%、24.86%和22.67%，其中在光伏发电输出功率波动频繁的多云天气总体提升最多。

同时，从表2中可以看到，所提方法总体NRMSE比其他预测方法分别降低1.31%、2.00%、2.97%、3.69%和3.21%，其中在晴转多云和阴雨天天气下提升较多；总体 NMAE比其他预测方法分别降低8.93%、7.24%、12.93%、16.65%和2.80%，其中在波动剧烈的多云天气和光伏发电输出功率急剧上升的多云转晴天气下提升较多；所提方法R-square在各种天气情况下均超过90%，优于所有对比方法，表明各个天气情况下所提方法均能对光伏发电输出功率进行较好拟合，具有一定适应性。

4 结论

实例证明所提的预测方法不仅预测准确度高、适应性强，而且建模过程简单，具有以下优点：

1)充分挖掘光伏混沌特性对RVM核函数泛化能力的影响，基于混沌特征确定RVM的基函数矩阵，再利用WOA对RVM参数进行寻优，相较WOA-RVM自回归预测方法，泛化能力得到提高；

2)在5种天气条件下的预测性能指标均高于优化后的LSSVM和SVM预测方法，方法的拟合能力指标R-square均超过90%，尤其在波动较大的天气下，跟踪性能更好；

3)通过提取光伏发电输出功率的混沌特征避免了多次寻找最邻近相点，预测过程简单，便于工程实践，为将超短期预测结果应用于光伏发电功率平滑控制领域奠定了理论基础。