一种计及能量枢纽不同运行模式的综合能源系统混合能量流求解方法

2021-06-10潘益王明深叶昱媛张宸宇缪惠宇郑建勇

现代电力 2021年3期

潘益，王明深,，叶昱媛，张宸宇，缪惠宇，郑建勇

（1.国网江苏省电力有限公司电力科学研究院，江苏省南京市 211103；2.东南大学电气工程学院，江苏省南京市 210096；3.国网江苏省电力有限公司检修分公司，江苏省南京市 211102）

0 引言

在能源系统转型与能源互联网的大背景下，综合能源系统（integrated energy system，IES）作为一种以电能为核心，协调优化多种异质能源形式、提供优质能源服务的物理载体，对提高能源综合利用率，促进可再生能源的消纳，实现多能互补以及能量的阶梯利用具有重要意义[1-3]。

综合能源系统多能流建模与能流求解是综合能源系统构建、运行管理的前提与基础。基于系统建模，开展混合潮流计算是后续优化调度与安全分析的核心。目前单一供能网络的能量流计算已有较为成熟的模型，但对于多种供能网络耦合的联合潮流计算，其研究还有待深入[4-5]。对于现有计算方法的研究，主要可以分为统一求解与解耦求解2大类[6-9]。统一求解法多通过建立多能源系统的矩阵方程并构造雅克比矩阵，结合牛顿–拉夫逊算法进行联合求解；解耦求解对各能源子系统进行独立求解，并通过能源耦合元件实现变量的迭代更新至误差在允许范围内。文献[10]针对热电耦合网络，同时利用这2类方法对热电潮流进行求解并进行了对比分析；文献[11]提出了一种适用于电/热/气综合能源系统的扩展牛–拉法多能流计算方法，实现多能流的统一计算。多能流的统一求解具有较高的普适性，较为直观，但模型较为复杂，对求解算法的要求较高，收敛性无法保证。文献[12]针对区域综合能源系统各能源子系统的不同耦合程度，提出了一种基于顺序求解思路的电力–天然气混合潮流算法，将天然气与电力网络分开求解，简化了计算的复杂度；文献[13]针对辐射型供热网，提出了热网潮流的前推回代计算方法并利用牛–拉法计算电网潮流，实现热电联合系统的解耦计算。

目前，上述的多能流求解方法多针对特定的拓扑进行构建，而不同的能量枢纽（energy hub，EH）运行方式将对整个能源网络的拓扑参数产生影响，进而改变混合能量流的分布情况，因此这些多能流求解方法未必兼顾不同运行模式，使得普适性难以得到保障。

本文针对电、气、热耦合型综合能源系统，构建不同能源子系统能量流的独立求解模型及方法，并提出以分布式顺序求解算法为核心的混合能量流计算流程，依托EH单元输入输出的钳制约束对各能源子系统的能流进行迭代校正，实现EH在不同运行模式下的能流流程化求解。

1 电–热–气综合能源系统建模

1.1 电-热-气能源子网络能流独立求解方法

对于电、热、气各能源子网络的独立建模，目前已有较为丰富的研究，具体建模方法可参考文献[14-16]，本文不再赘述。

综合能源系统中的电力子系统潮流采用传统牛–拉法进行求解。对于结构简单的辐射状热力网，可采用前推回代法[13]进行温度、流量的迭代计算。对于较复杂的多源环状热网，为提高求解效率，考虑以温度–流量模型[17]为基础，改写为如式（1）描述的热网状态矩阵方程：

式中：HSP为系统已知的热功率信息，当HSP对应EH与热网交互的热功率，M=mq=−Am；当HSP对应节点热功率，M=m；m与mq分别表示各管道支路流量以及流经热源或负荷节点的流量；K为管道阻力系数矩阵[10]；B表示支路–回路关联矩阵；Cs，bs，Cr，br分别表示供热、回水网络拓扑、热媒流量与节点温度有关的矩阵，具体构造方法如文献[11]所述。Ts与Tr分别包括热源EH侧供回水温度以及热媒汇聚节点供回水温度2部分。

根据状态矩阵方程，利用牛–拉法，构造雅克比矩阵对式（1）进行迭代求解，其中待求状态量包括xh=[Ts,Tr,m]。

天然气网络能流计算时同样考虑先将系统潮流方程组改写为式（2）所示的矩阵形式，进而构造天然气系统潮流矩阵方程：

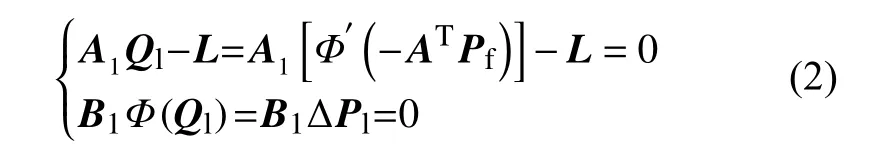
式中：A1与B1分别表示为简约的节点-管路关联矩阵与管路–节点关联矩阵；AT为节点–管路关联矩阵的转置；Pf与ΔPl分别代表节点压力降矩阵与管道压力降矩阵；Ql与L分别代表管道流量矩阵以及节点气负荷矩阵；Φ(•)与Φ'(•)分别代表流量函数与压力降函数，两者互为反函数，天然气系统潮流矩阵方程的具体构造流程可详见参考文献[18]。基于天然气系统潮流矩阵方程，同样利用牛–拉法，构造雅克比矩阵对式（2）进行迭代求解，其中待求状态量包括xg=[Pf, Ql]。

1.2 EH建模

各供能网络间的耦合与多能形态的转化通常由IES的EH完成。目前通常利用能源集线器模型[19-20]对EH单元进行描述。

EH内部包含较多的能量转换与存储环节，不同的能源元件配置与组合形式将对EH的外部输出特性产生影响，本节选择2种典型的结构进行分析说明。

图1所示为第1类EH结构，主要分布在负荷侧，输入端连接外部多能流网络负荷节点，输出端直接向用户侧供能，外部能源网络输入的各种形式能量经EH单元转换为满足用户多元需求的电、热、冷、气负荷，此类EH的输入输出耦合关系可表示为

图2所示为第2类EH结构，主要分布在源测，为能源网络末端的多元负荷供能。输入端主要连接天然气站负荷节点以及各类分布式能源，输出端主要连接能源网络的源节点，输出的冷热电气能通过各类输能网络输送至用户侧，此类EH的输入输出耦合关系可表示为

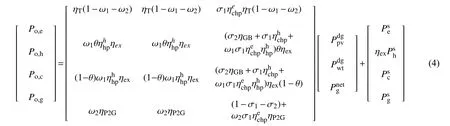
式中：Le、Lh、Lc、Lg分别为电、热/冷、气负荷；ω1与ω2为电能分配系数；θ为热能分配系数；σ为天然气分配系数；ηT、、ηEB、ηEC、ηAC、ηex分别表示变压器效率、热电联产（combined heat and power，CHP）机组的电效率、热效率、电锅炉制热效率、电制冷机与吸收式制冷机的制冷效率以及热交换器效率；与ηGB分别表示热泵与燃气锅炉的制热效率；与分别代表分布式光伏与风机的发电功率；ηP2G为P2G设备的转换效率；以及分别代表电、热、冷、气储能单元功率。

1.3 EH运行模式划分

根据EH在能源传输网络中的作用，可从能源网络层面将其划分为4种运行模式。

图1 第1类能量枢纽结构Fig.1 Structure of the first type of energy hub

图2 第2类能源枢纽结构Fig.2 Structure of the second type of energy hub

模式1：此模式下各EH节点对于电–热–气输能网络而言均为负荷节点，综合能源网络的平衡节点分别由外部电源（上级电网）、热源（上级换热站）及气源（上级燃气站）承担，各EH从各输能网络获得能量后经转换直接向所接负荷供能，其输入输出约束关系同式（3），在多能流稳态计算时各能源网络可独立进行求解。

模式2：此模式下选择某一具有充足容量、稳定热能输出的EH作为热力网平衡节点，即热网侧的热力流平衡由此EH实现，其余EH视为PV/PQ节点、普通热源节点及天然气负荷节点，EH的输入输出约束关系同式（4）。此时，各EH所接入的电力网侧潮流由外部电网平衡，因此各EH单元的功率输出波动仅对平衡节点处的EH单元出力产生影响，各能源网络处于弱耦合状态。

模式3：此模式下选择某一具有充足容量、稳定、动态响应快速的EH作为电力网络侧的平衡节点，其余EH节点均视为PV/PQ节点、普通热源节点及天然气负荷节点。此时，各能源网络的耦合状态与模式2类似。

模式4：此模式下选择两个EH分别作为电力网与热力网的平衡节点，其余EH节点均视为PV/PQ节点、普通热源节点及天然气负荷节点。此时，各能源网络处于强耦合状态，电网侧及热网侧的潮流均由EH单元实现平衡与调节。

2 综合能源系统混合能量流计算

2.1 综合能源网络状态量分析

在开展综合能源系统稳态能流计算前，需要明确各能源网络所包含的状态量。电力/热力/天然气供能网络通过EH进行耦合，各网络间根据耦合程度的不同将获得不同的运行状态量。

对于电力网络，状态量主要包括节点电压幅值与相角、节点注入的有功与无功功率，节点类型主要有平衡节点、PV与PQ节点3类；对于热力网络，状态量主要包括管道热媒流量、供回水温度以及节点注入的热功率，节点类型主要有热源节点（又分为平衡热源节点与普通热源节点2类）、负荷节点（已知负荷热功率及节点回水温度）以及其他节点；对于天然气网络，状态量主要包括节点压力及管道气流量，节点类型主要包括压力已知节点和流量已知节点，其中压力已知节点多为气源节点且至少有一个气源节点设置为天然气平衡节点，流量已知节点则多为负荷节点。各能源网络具体的节点类型及待求状态量等信息如表1所示。

2.2 混合能量流求解方法

综合能源系统多能流求解方法主要有统一求解与分布式顺序求解2类。统一求解法虽然能提供统一的求解模式，便于理解，但在求解时包含大量的待求解变量，雅克比矩阵维度巨大，求解复杂度较高，且模型收敛性也无法保证。而分布式顺序求解法能够充分利用电、气、热各网络潮流已有的计算求解模型，实现各能源网络的独立求解，大大提高了求解效率，缩减了求解复杂度。因此，本文主要依托分布式顺序求解法对前节所述的EH 4种典型运行模式开展多能流求解方法的研究。

图3所示为本文综合能源系统多能流求解流程。模式1、模式2与模式3求解流程类似，各能源子系统利用各自现有成熟的求解模型依次进行独立求解；模式4由于各能源系统耦合程度较深，求解流程相对更为复杂。选择模式1与模式4两种具有代表性的运行场景下的能流计算过程进行分析说明。

1）对于模式1，其求解流程相对简单，归纳如下：

步骤1：获取各EH输出端所接的气、电、热、冷负荷信息；Lg、Le、Lh、Lc，根据式（3）描述的EH单元内部耦合关系矩阵分别计算各EH输入功率，各EH单元可视为电力、热力及天然气网络对应接入节点的等效负荷；

步骤2：热力系统潮流的独立求解；基于热网侧潮流计算，热网中各循环水泵的耗电功率等效为电力网络侧的电负荷；

表1 电–热–气综合能源系统状态量信息Table 1 Information of state variables for IES containing electricity, thermal and gas networks

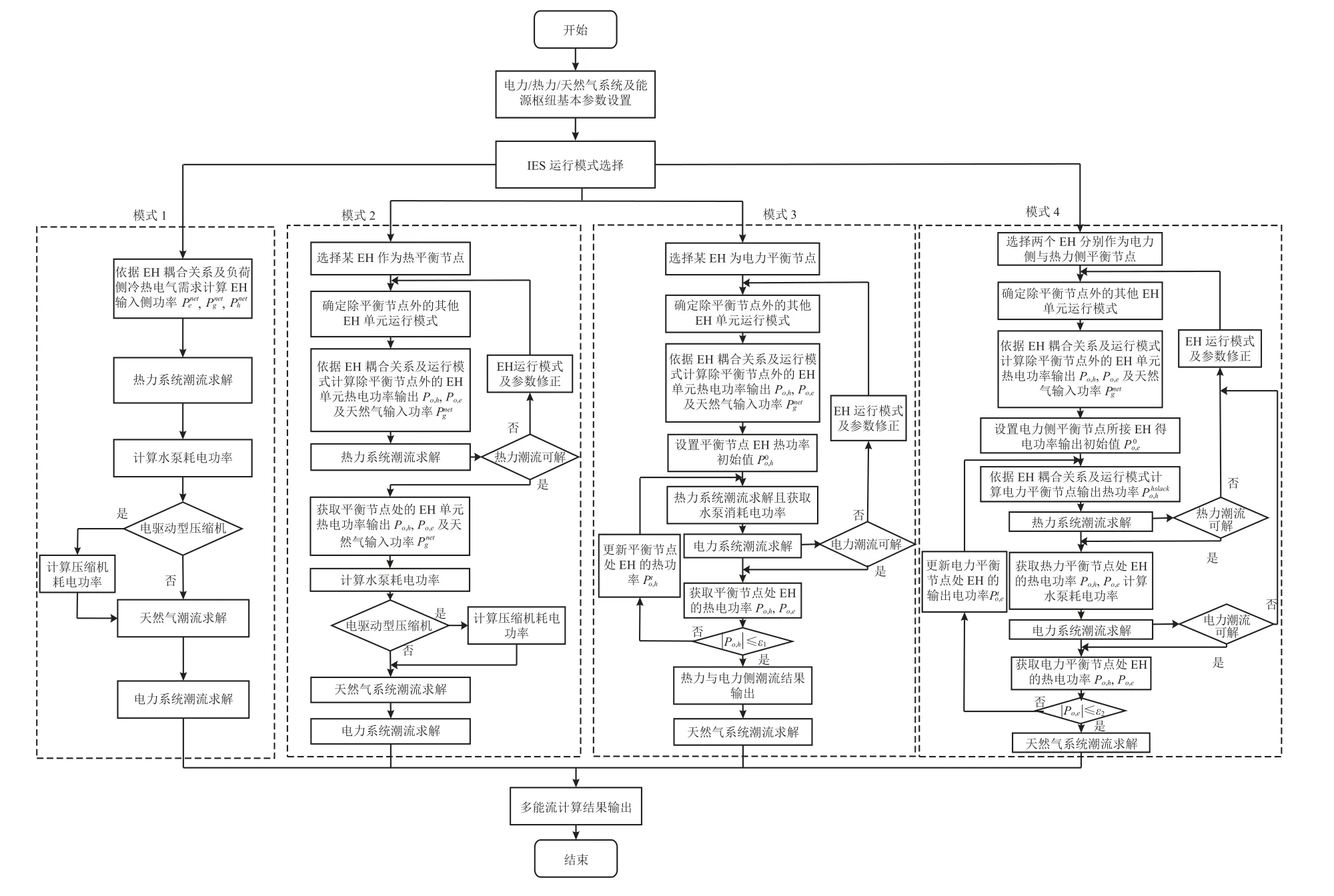
图3 综合能源系统多能流求解流程Fig.3 Flowchart for multi-energy flow calculation of IES

步骤3：天然气系统潮流的独立求解。若天然气系统中含有电力驱动型压缩机，则还需额外计算压缩机的耗电功率，等效至电力网络侧的电负荷；

步骤4：基于电力网络侧已知参数，利用牛–拉法求解电力网络潮流；

步骤5：输出电/气/热网络多能流计算结果。

2）对于模式4，由于同时选择两个EH单元分别作为电力与热力系统的平衡节点，因此各能源子系统间的耦合程度最高。与其他几种模式相比，模式4在各能源子系统能流独立求解的基础上，需要额外增加考虑耦合元件输出功率偏差约束的联合迭代求解过程。可归纳如下。

步骤1：首先选择两个EH单元分别作为电力侧与热力侧的平衡节点，同时确定除平衡节点外的其他EH单元运行模式；

步骤2：依据EH耦合关系及运行模式计算除平衡节点外的EH单元热电输出功率Po,h、Po,e及输入侧天然气功率

步骤3：进入热电系统潮流联合迭代求解过程。

②其次，根据EH耦合关系及运行模式计算电力平衡节点的输出热功率

③基于热力侧已知条件，进行热力系统的潮流求解，若热力侧潮流不收敛，则需修正EH单元的运行模式及相关运行参数，返回步骤2，直至热力潮流收敛；

④基于当前迭代过程中的热力潮流计算结果，获取热力平衡节点处的EH单元输出热电功率并计算水泵耗电功率；

⑤基于电力侧已知条件，进行电力子系统的潮流计算，若电力侧潮流不收敛，则同样需修正EH单元的运行模式及相关运行参数，返回步骤2，直至电力潮流收敛；

⑥获取电力平衡节点处EH单元的热电输出功率，计算相邻两次迭代过程的电力平衡节点处EH单元电输出功率偏差，若满足收敛条件则热电系统潮流联合迭代求解过程完成，输出热力/电力侧的潮流计算结果，反之，则需用当前第t次迭代时电力平衡节点处EH单元的电输出功率初始化第（t+1）次迭代过程的，重新依次执行步骤3，直至迭代过程完成；

步骤4：进行天然气系统潮流的独立求解。同样需要处理不同压缩机类型的等效电力负荷计算问题，处理方式与模式1相同；

步骤5：输出电/气/热网络多能流计算结果。

此外，若考虑P2G技术的应用，则考虑采用合同电转气的商业模式[21]，将P2G环节对应的天然气与电力节点分别等效为定流量节点与PV节点，进而参与多能流的计算。

3 算例分析

3.1 综合能源网络状态量分析

为验证本文所提多能流计算方法的有效性，以改进的IEEE14节点电力系统、15节点区域热力系统、14节点天然气系统以及两个EH（EH1和EH2）构成的电–热–气综合能源系统作为算例进行仿真分析。

如图4所示，电、气、热各能源子系统通过两个EH单元进行耦合。天然气子系统的平衡节点为Gs1，通过外部气源输入调节整个天然气网络的平衡，气源节点的压力已知为1000 psia，压缩机为燃气轮机驱动型。EH1的热网侧接入点为Hs6，电网侧接入点为Bs3，天然气网接入点Gs14视为天然气负荷节点；EH2的电网侧接入点为Bs1，热网侧接入点为Hs7，天然气接入点Gs3视为天然气负荷节点。其中，热力子系统中各热力负荷节点回水温度设置为30 ℃，热源节点供水温度为90 ℃。两个EH的拓扑结构如图2所示，但暂不考虑输冷环节，因此忽略吸收式制冷机及蓄冷等设备。EH单元的配置参数以及各能源子系统的基本参数见附表A1—A6。

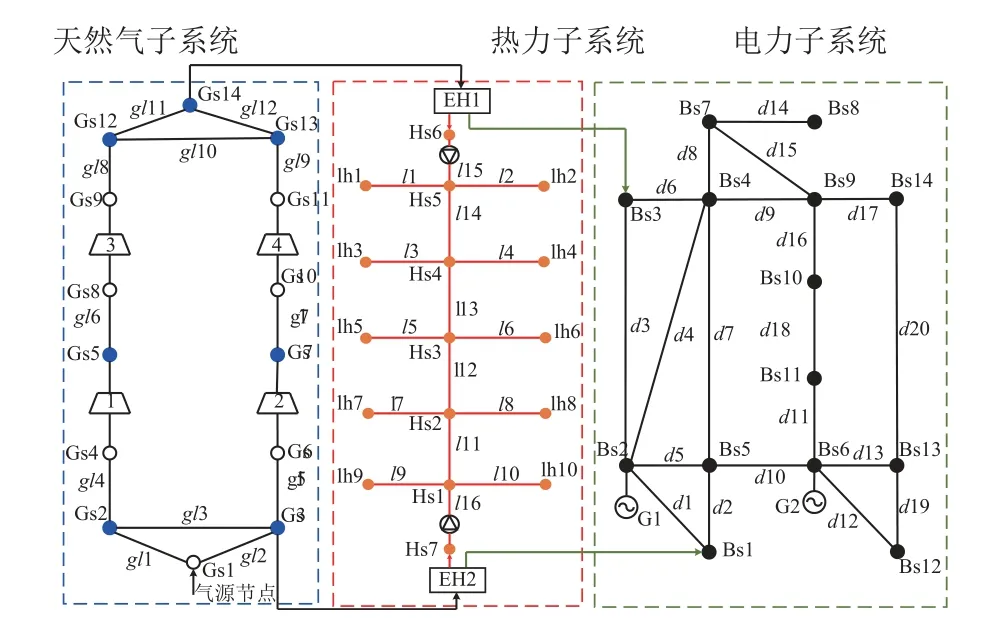
图4 电-热-气综合能源系统算例结构Fig.4 Case diagram of IES containing electricity, thermal and gas networks

3.2 仿真结果分析

基于本文所提方法，利用MATLAB编写程序，针对2种不同场景对算例进行多能流求解与分析，计算结果如表2—6所示。

场景1：运行于模式4。EH1的热网侧接入点Hs6视为热力平衡节点，电网侧接入点Bs3视为PV节点，天然气网接入点Gs14视为天然气负荷节点；EH2的电网侧接入点Bs1视为电力平衡节点，热网侧接入点Hs7视为普通热源节点，天然气接入点Gs3视为天然气负荷节点。

场景2：运行于模式2。电力侧并网运行，并网点（电力平衡节点）为Bs6，外部电网等效为G2，即电力侧网络的平衡由G2调节。EH1的热网侧接入点Hs6视为热力平衡节点，电网侧接入点Bs3视为PV节点，天然气网接入点Gs14视为天然气负荷节点。而EH2的电网侧接入点Bs1视为PV节点，热网侧接入点Hs7视为普通热源节点，天然气接入点Gs3视为天然气负荷节点。

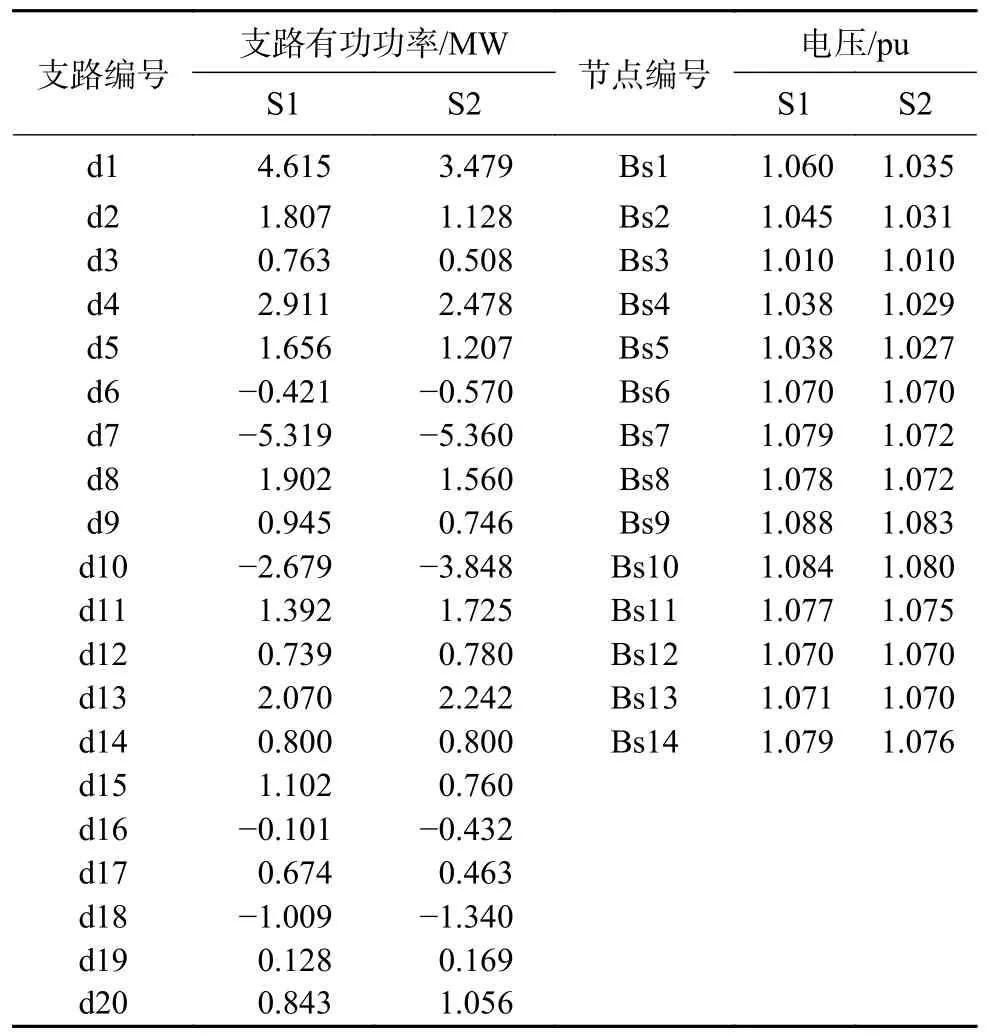
表2 电力子系统潮流计算结果Table 2 Calculation results for electricity flow

表3 电力子系统各发电单元出力Table 3 Output of each electricity generation unit

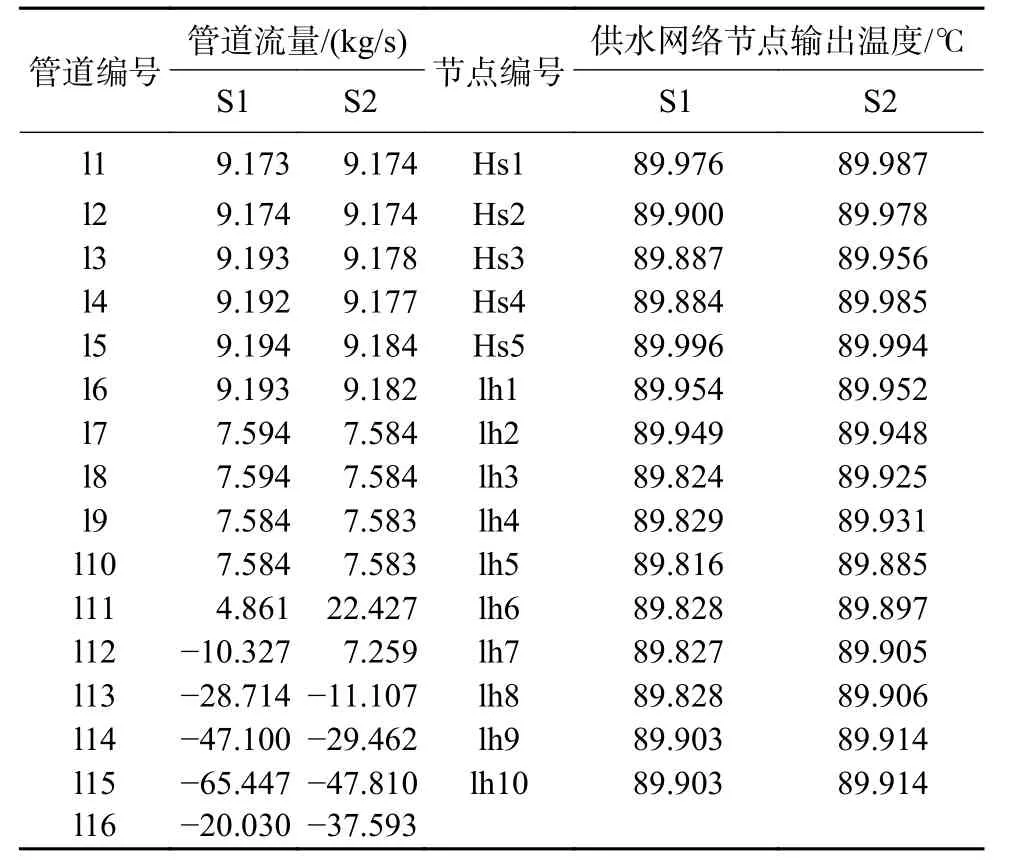
表4 热力子潮流计算结果Table 4 Calculation results for thermal flow

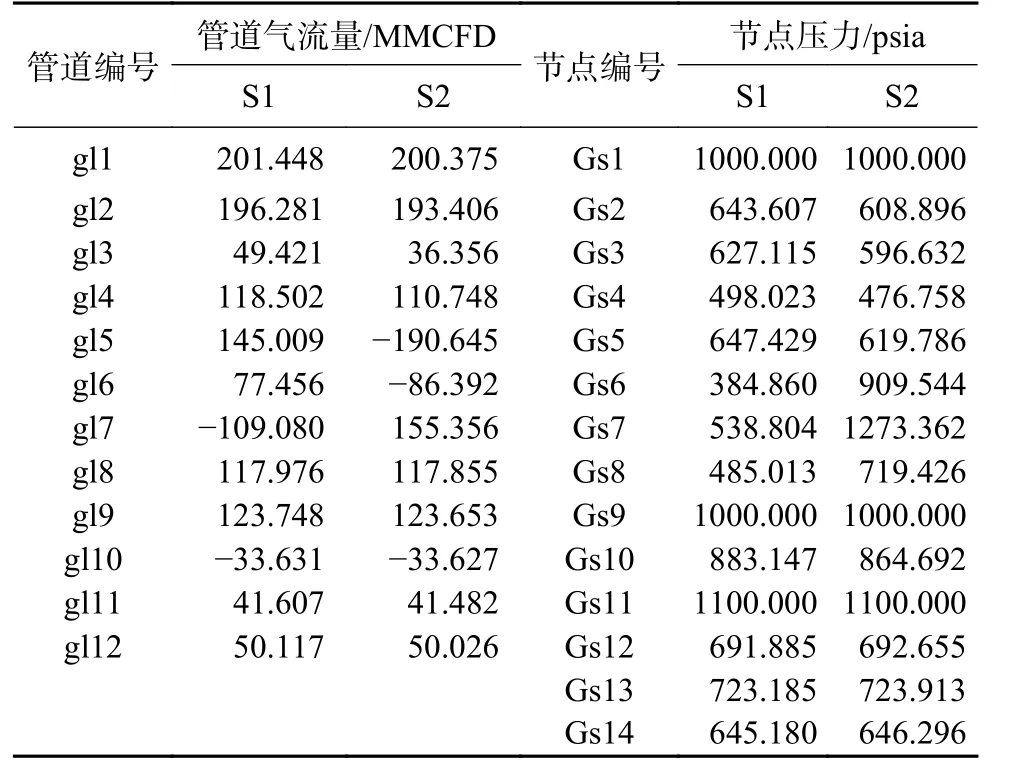
表5 天然气子系统潮流计算结果Table 5 Calculation results of natural gas flow of natural gas subsystem

表6 天然气子系统压缩机耗气量计算结果Table 6 Gas consumption calculation results of the compressors of natural gas subsystem

根据混合潮流计算结果可知，对于电力子系统，2种不同场景下支路的有功潮流分布及节点电压分布产生一定差异，但整体数值较为接近。场景2中EH2的有功出力设置为8 MW，且各PV节点的无功储备充足，经计算平衡节点对应的G2机组有功出力为6.76 MW，2种场景下的节点电压幅值均在0.9～1.1 pu之间，未出现电压越限情况。此外2种场景仅运行模式不同，网络参数基本保持一致，因此2种场景下的潮流未发生明显转移，潮流计算结果较为接近。

对于热力子系统，由计算结果可知，不同运行场景下的负荷节点管道流量变化较小，但主管道l11—l16对应的管道热水流量差异明显。两种场景下，EH1的热网接入点均为热力平衡节点，承担热网侧的潮流平衡调节。场景1下EH1与EH2的热功率输出分别为16.43 MW与5.03 MW，管道热水汇流节点为Hs2；场景2下EH1与EH2的热功率输出分别为12 MW与9.43 MW，管道热水汇流节点变为Hs3。可见，EH1热源输出热功率的降低使得EH1附近的管道l14、l15流量降低，而EH2热源附近管道l11与l16的流量随着EH2单元热功率出力的增加而增大。

对于天然气子系统，部分节点等效气负荷的改变使得天然气管道流量与节点压力分布产生变化。场景2下管道gl5、gl6、gl7的气流量相较于场景1明显增加，节点Gs6、Gs7、Gs8压力值也存在明显提升，可能对系统的安全稳定运行产生影响。因此有必要考虑IES系统在不同运行模式下的能流分布情况，识别脆弱环节，通过合理配置EH单元及网络参数，保障系统在不同运行模式下均具有足够的安全裕度。

此外，图5展示了本文所提多能流求解算法在不同场景下的收敛曲线。由图5可知，此算法有着较为理想的收敛速度，仅需经过少量迭代即可收敛到很小的误差范围内，从而验证了本节算法的有效性。同时，由于场景2下热/电/气网络的耦合程度相对较低，求解复杂度较低，因此与其他场景相比具有更快的收敛速度。

图5 不同场景下的收敛曲线Fig.5 Convergence curves in different cases

此外，基于本文所提能量流求解方法，进一步分析EH单元在不同运行模式下IES的N-1静态安全校验情况。同样以场景1与场景2为例进行分析，对应的关键元件N-1校验结果如附图B1与附图B2所示。由图可见，对于场景1，EH2单元处于离网运行状态，各能源子系统耦合程度较高，在关键元件（发电机组G1、G2）N-1情况下，电力侧的潮流越限将通过耦合单元影响其他能源系统的运行状态，可能引起有故障的跨能源系统传播，增大了系统整体的安全运行风险。对于场景S2，EH2单元运行于并网状态，系统整体的耦合程度较低，电力侧安全运行的调节能力更强，使得系统具有比场景S1更为理想的静态安全性能。

可见，EH单元的不同运行模式将对IES系统整体运行状态产生影响，强耦合下的IES系统在具有高灵活性与互补互济特性的同时往往更容易引起较低的安全运行裕度。同时也验证了本文所提能流计算方法在系统运行状态与安全性分析方面的有效性。